题解 | #B.Distance# 2023牛客暑期多校6
B.Distance
贪心(?)
题目大意
对于两个大小相同的多重集 A , B \mathbb{A},\mathbb{B} A,B ,可以选择其中任一元素 x x x 执行操作 x = x + 1 x=x+1 x=x+1 任意次数,最少的使得 A , B \mathbb{A},\mathbb{B} A,B 相同的操作次数记为 C ( A , B ) C(\mathbb{A},\mathbb{B}) C(A,B)
不同大小的 A , B \mathbb{A},\mathbb{B} A,B 视为 C ( A , B ) = 0 C(\mathbb{A},\mathbb{B})=0 C(A,B)=0
现在,给定两个大小为 n n n 的多重集 S , T \mathbb{S},\mathbb{T} S,T ,求对于 S , T \mathbb{S},\mathbb{T} S,T 的所有子集 A , B \mathbb{A},\mathbb{B} A,B ,最少操作次数之和 ∑ A ⊆ S ∑ B ⊆ T C ( A , B ) \sum\limits_{\mathbb{A} \subseteq \mathbb{S}}\sum\limits_{\mathbb{B} \subseteq \mathbb{T}} C(\mathbb{A},\mathbb{B}) A⊆S∑B⊆T∑C(A,B) 的值
具有相同值的两个元素视为不同元素,答案取模
解题思路
对于某对子集 A , B \mathbb{A},\mathbb{B} A,B ,为了使他们相同的操作次数最少,我们会将他们排序的元素后一一对应,使每一对中较小的数变成较大的数//假设 a i a_i ai 与 b i b_i bi 对应,他们在这次变化中贡献的操作次数显然是 ∣ a i − b i ∣ |a_i-b_i| ∣ai−bi∣
那么换一种角度考虑,对于原多重集 S , T \mathbb{S},\mathbb{T} S,T ,任取一对数 a i , b j a_i,b_j ai,bj ,考虑它们俩对应的方案数 c n t i , j cnt_{i,j} cnti,j ,那么它们在全部方案中贡献的总操作次数即为 ∣ a i − b i ∣ × c n t i , j |a_i-b_i|\times cnt_{i,j} ∣ai−bi∣×cnti,j
由于我们的操作策略是排序后对应,因此先对 S , T \mathbb{S},\mathbb{T} S,T 进行排序//
选定两个数 a i , b j a_i,b_j ai,bj 后,它们在 S , T \mathbb{S},\mathbb{T} S,T 中的位置前面选 k k k 对数的方案数为 ∑ k = 0 m i n ( i − 1 , j − 1 ) C i − 1 k C j − 1 k = C i + j − 2 k \sum\limits_{k=0}^{min(i-1,j-1)}C_{i-1}^kC_{j-1}^k=C_{i+j-2}^k k=0∑min(i−1,j−1)Ci−1kCj−1k=Ci+j−2k (范德蒙德卷积)
同理,它们在 S , T \mathbb{S},\mathbb{T} S,T 中的位置后面选 k k k 对数的方案数为 C 2 ∗ n − i − j k C_{2*n-i-j}^k C2∗n−i−jk
总方案数为 c n t i , j = C i + j − 2 k C 2 ∗ n − i − j k cnt_{i,j}=C_{i+j-2}^kC_{2*n-i-j}^k cnti,j=Ci+j−2kC2∗n−i−jk ,乘以两数之差的绝对值即为它们对答案的总贡献//
预处理组合数,枚举 i , j i,j i,j 求和即可
时间复杂度
O ( n 2 ) O(n^2) O(n2)
参考代码
参考代码为已AC代码主干,其中部分功能需读者自行实现
#define N 2005
void solve()
{ll n,t;cin >> n;vector<ll> a(n),b(n);for(auto &x:a) cin >> x;for(auto &x:b) cin >> x;ll re=0;SORT(a);SORT(b);FORLL(i,0,n-1) FORLL(j,0,n-1)addto(re,mul(abs(a[i]-b[j]),mul(Get_Combination(i+j,i),Get_Combination((n-i-1)+(n-j-1),(n-i-1)))));cout << re << endl;
}
相关文章:

题解 | #B.Distance# 2023牛客暑期多校6
B.Distance 贪心(?) 题目大意 对于两个大小相同的多重集 A , B \mathbb{A},\mathbb{B} A,B ,可以选择其中任一元素 x x x 执行操作 x x 1 xx1 xx1 任意次数,最少的使得 A , B \mathbb{A},\mathbb{B} A,B 相同的操作次数记为 C ( A , B ) C(\m…...

【flink】开启savepoint
先启动一个任务 flink run -c com.yang.flink.CDCJob test-cdc.jar开启savepoint 命令: flink savepoint JobID 文件地址 flink savepoint e929a11d79bdc5e6f140f2cfb92e1335 file:///workspace/flinkSavepoints/backend这样就开启好了 操作中的错误 详细信…...

【C++】开源:事件驱动网络库libevent配置使用
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍事件驱动库libevent配置使用。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下…...

业务测试——历史数据
业务测试历史数据的必要性 1.保留上一版本的呈现效果以及数据正确性 2.做发版前后数据、样式一致性校验 3.后端处理历史数据,覆盖各类场景,保证客户的现有数据不会被影响,造成线上事务 4.为测试过程的覆盖度以及产品迭代的质量保驾护航 如何…...
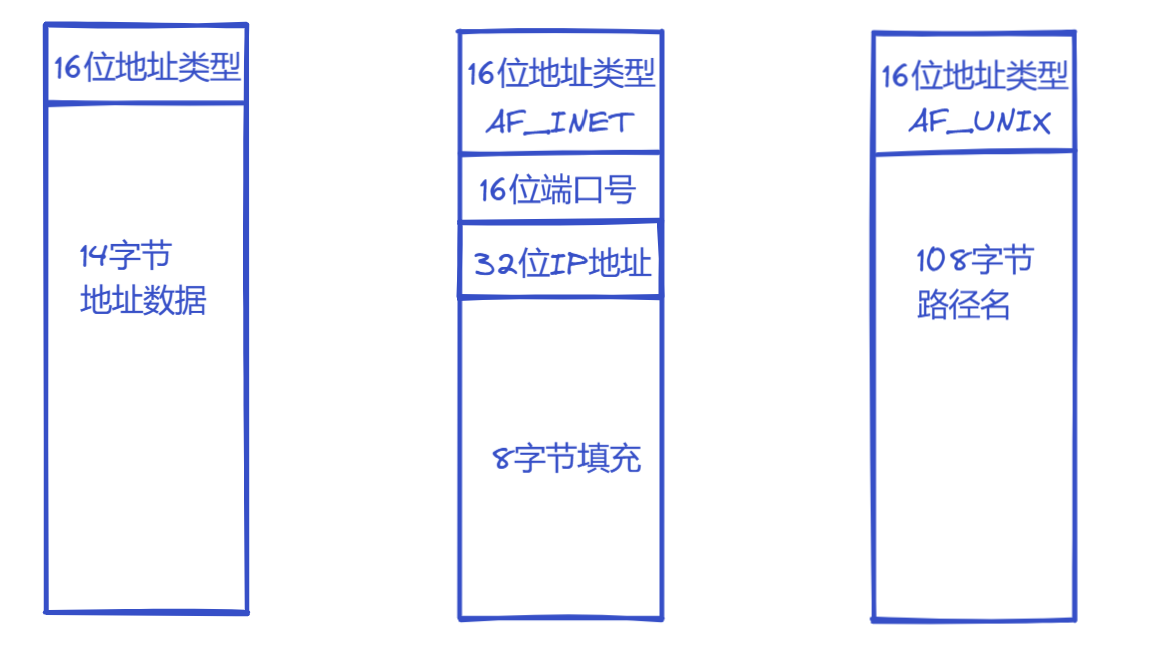
【Linux】计算机网络套接字编写
文章目录 前言TCP协议和UDP协议网络字节序socket接口sockaddr结构1.创建套接字 cs2.绑定端口号 s3.监听socket s4.接受请求 s5.建立连接 c 地址转换函数字符串转in_addrin_addr转字符串 recvfrom和sendto 前言 上篇文章我们学习了计算机网络分层,了解了网络通信的本…...
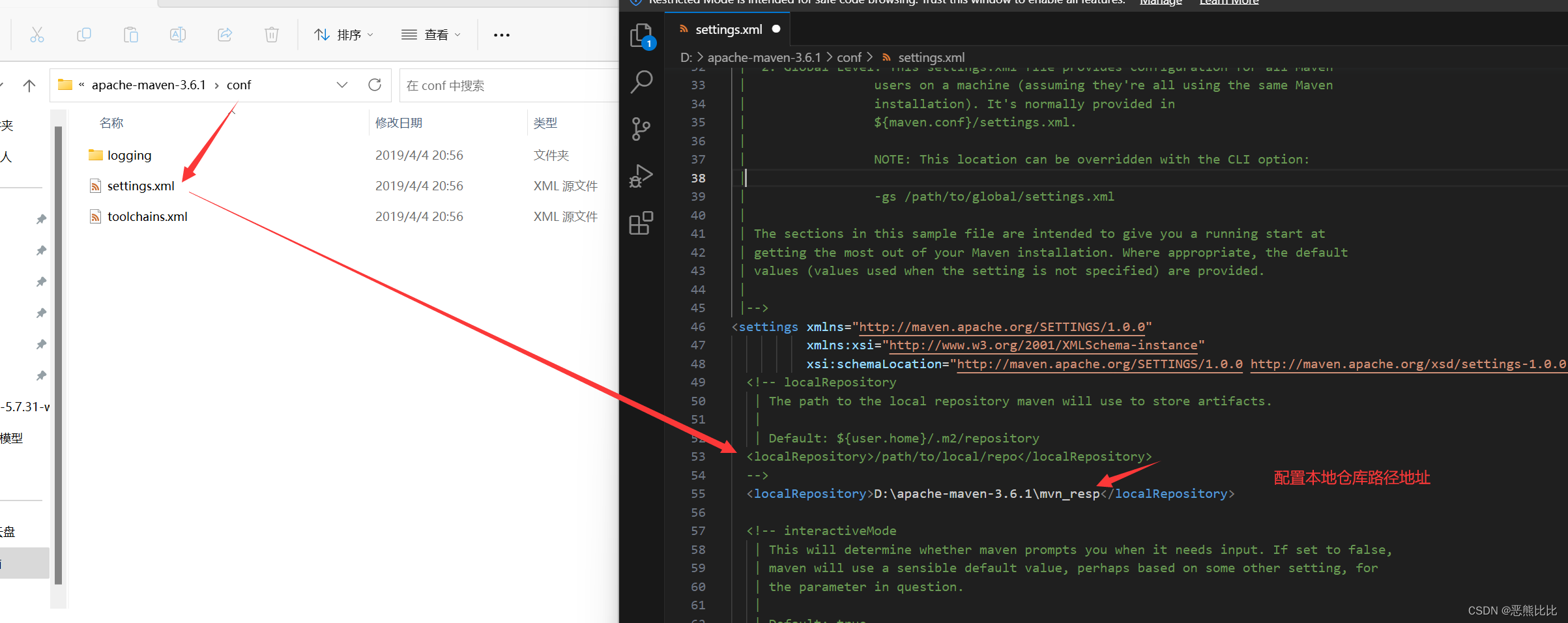
Maven-学习笔记
文章目录 1. Maven简介2.Maven安装和基础配置3.Maven基本使用4.Maven坐标介绍 1. Maven简介 概念 Maven是专门用于管理和构建Java项目的工具 主要功能有: 提供了一套标准化的项目结构提供了一套标准化的构建流程(编译,测试,打包,…...
WebGL Shader着色器GLSL语言
在2D绘图中的坐标系统,默认情况下是与窗口坐标系统相同,它以canvas的左上角为坐标原点,沿X轴向右为正值,沿Y轴向下为正值。其中canvas坐标的单位都是’px’。 WebGL使用的是正交右手坐标系,且每个方向都有可使用的值的…...

【Codeforces】 CF468C Hack it!
题目链接 CF方向 Luogu方向 题目解法 令 ∑ i 1 1 e 18 f ( i ) ≡ g ( g < a ) ( m o d a ) \sum_{i1}^{1e18}f(i)\equiv g(g<a)(mod \;a) ∑i11e18f(i)≡g(g<a)(moda) 那么 ∑ i 2 1 e 18 1 f ( i ) ≡ g 1 \sum_{i2}^{1e181}f(i)\equiv g1 ∑i21e181f…...
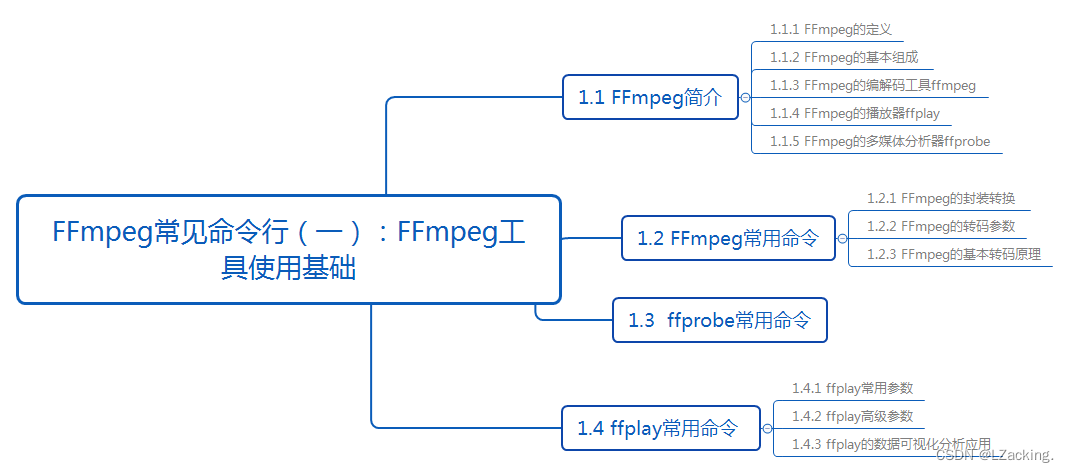
FFmpeg常见命令行(一):FFmpeg工具使用基础
前言 在Android音视频开发中,网上知识点过于零碎,自学起来难度非常大,不过音视频大牛Jhuster提出了《Android 音视频从入门到提高 - 任务列表》。本文是Android音视频任务列表的其中一个, 对应的要学习的内容是:FFmpe…...
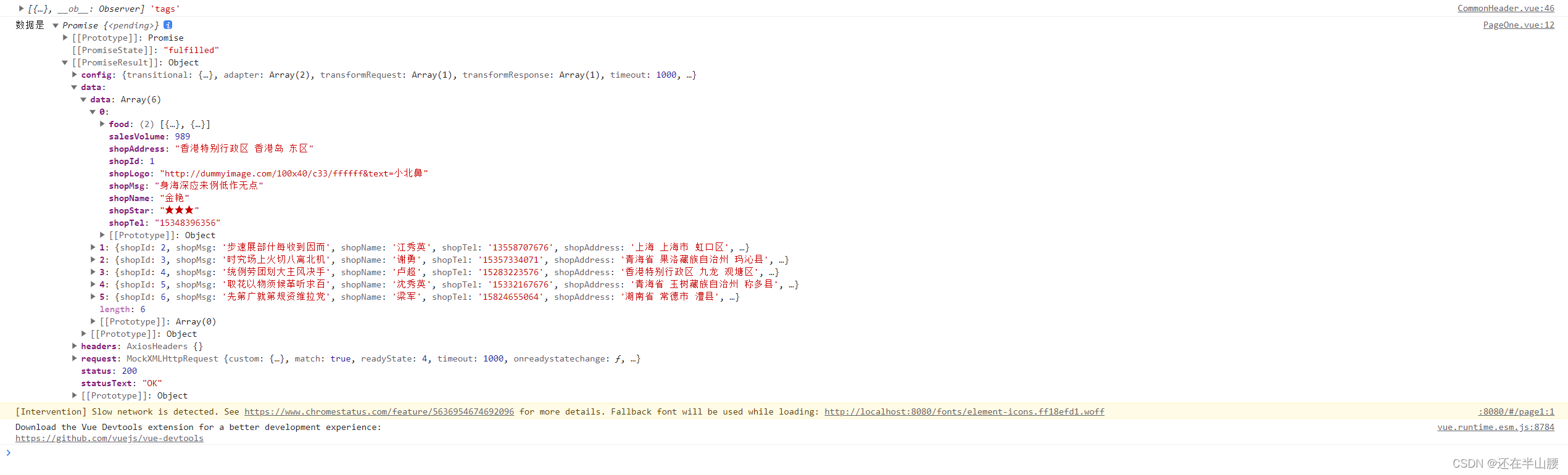
Mock.js的基本使用方法
官网网址:Mock.js (mockjs.com) 当前端工程师需要独立于后端并行开发时,后端接口还没有完成,那么前端怎么获取数据? 这时可以考虑前端搭建web server自己模拟假数据,这里我们选第三方库mockjs用来生成随机数据…...
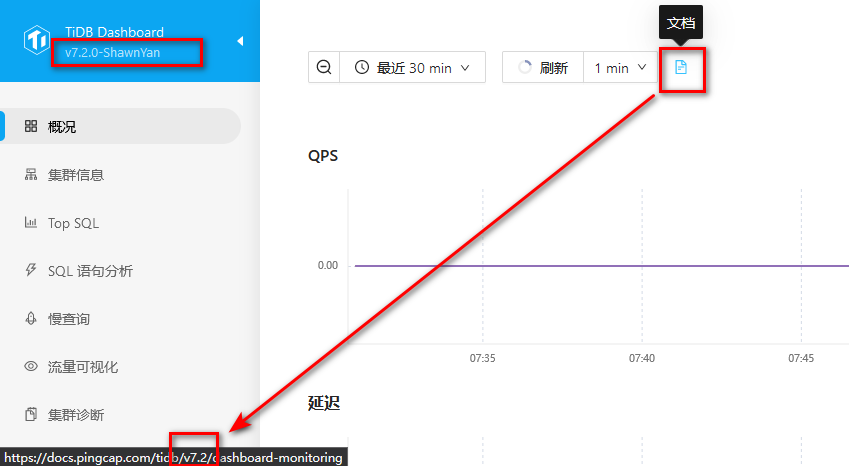
TiDB 源码编译之 PD/TiDB Dashboard 篇
作者: ShawnYan 原文来源: https://tidb.net/blog/a16b1d46 TiDB TiDB 是 PingCAP 公司自主设计、研发的开源分布式关系型数据库,是一款同时支持在线事务处理与在线分析处理 (Hybrid Transactional and Analytical Processing, HTAP) 的融…...
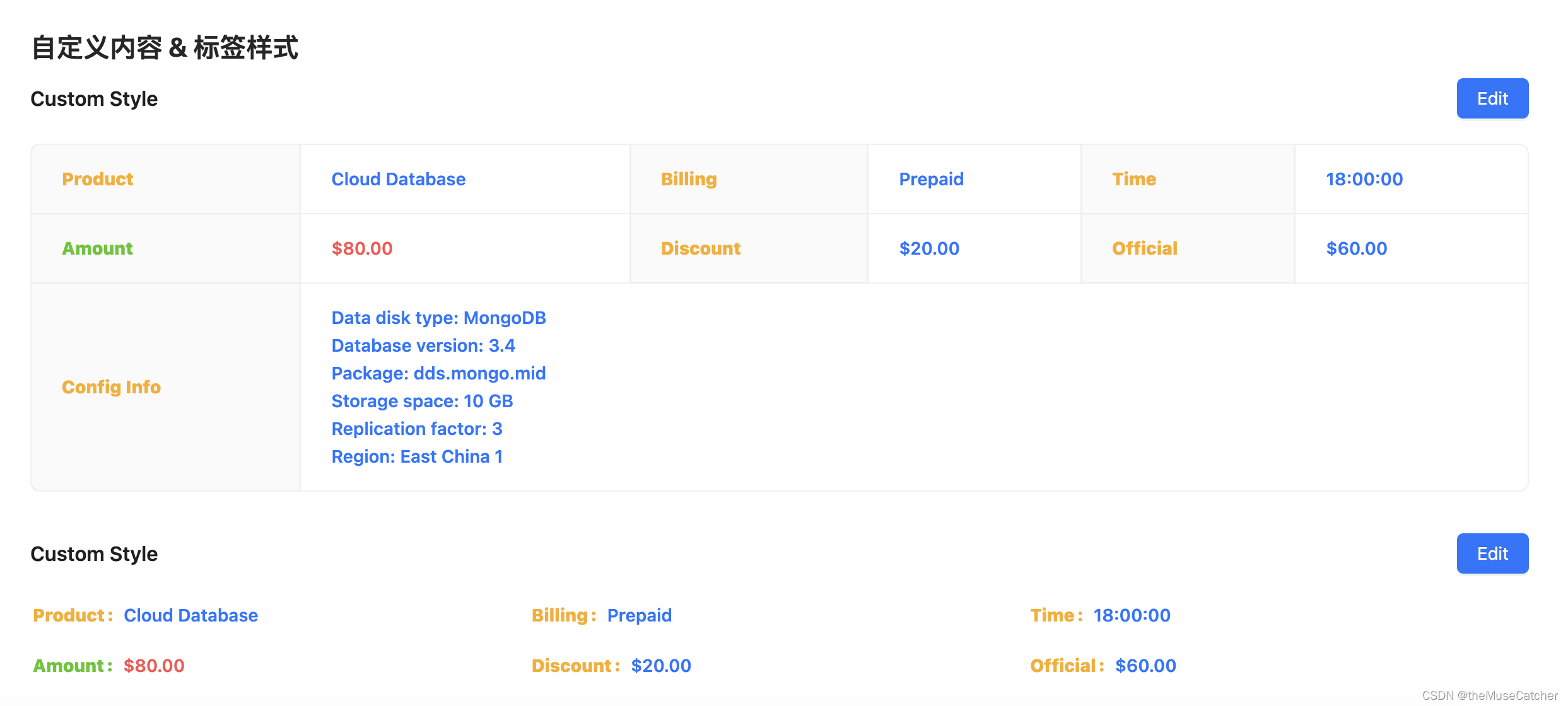
Vue3描述列表(Descriptions)
😁 整体功能效果与 ant design vue 保持高度一致 😁 包含两种组件:Descriptions 和 DescriptionsItem(必须搭配使用!) 效果如下图:在线预览 APIs Descriptions 参数说明类型默认值必传title…...
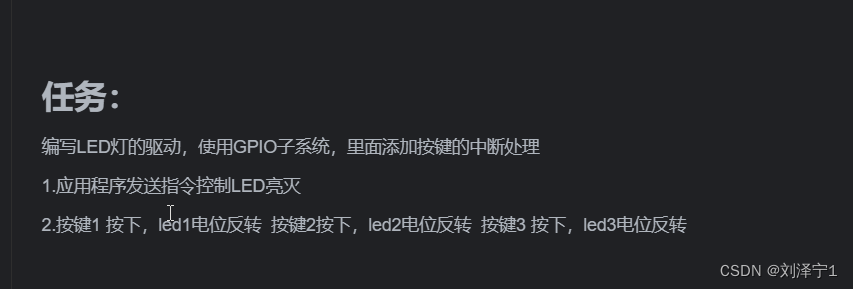
【驱动开发day8作业】
作业1: 应用层代码 #include <stdlib.h> #include <stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <unistd.h> #include <string.h> #include <sys/ioctl.h>int main(int…...

yxBUG记录
1、 原因:前端参数method方法名写错。 2、Field ‘REC_ID‘ doesn‘t have a default value 问题是id的生成问题。 项目的表不是自增。项目有封装好的方法。调用方法即可。 params.put("rec_id",getSequence("表名")) 3、sql语句有问题 检…...
uniapp引入inconfont自定义导航栏
app,h5端引入 uniapp本身的全局设置中有个iconfontsrc属性 所以只需要 1.iconfont将需要的icon添加至项目 2.下载到本地解压后,将其中的ttf文件,放在static静态目录下 3.在page.json中对全局文件进行配置tabBar(导航图标) “iconfontSrc”: “static/font/iconfont.ttf”, …...
OSLog与NSLog对比
NSLog: NSLog的文档,第一句话就说:Logs an error message to the Apple System Log facility.,所以首先,NSLog就不是设计作为普通的debug log的,而是error log;其次,NSLog也并非是printf的简单…...
全网最细,Fiddler修改接口返回数据详细步骤实战,辅助接口测试...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 在测试的过程中&a…...
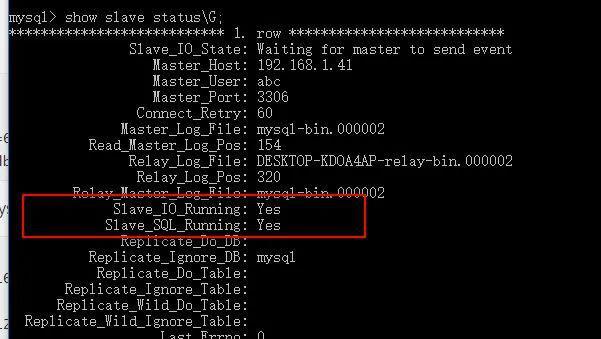
Mysql自动同步的详细设置步骤
以下步骤是真实的测试过程,将其记录下来,与大家共同学习。 一、环境说明: 1、主数据库: (1)操作系统:安装在虚拟机中的CentOS Linux release 7.4.1708 (Core) [rootlocalhost ~]# cat /etc/redh…...
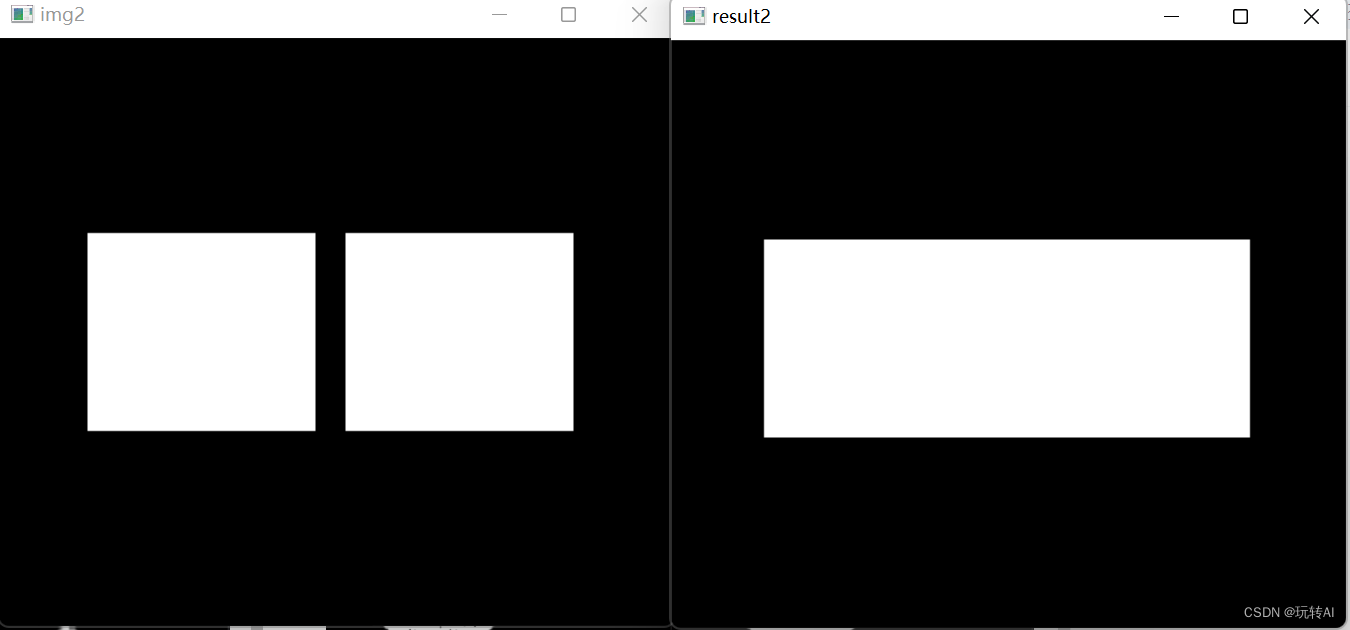
opencv-38 形态学操作-闭运算(先膨胀,后腐蚀)cv2.morphologyEx(img, cv2.MORPH_CLOSE, kernel)
闭运算是先膨胀、后腐蚀的运算,它有助于关闭前景物体内部的小孔,或去除物体上的小黑点,还可以将不同的前景图像进行连接。 例如,在图 8-17 中,通过先膨胀后腐蚀的闭运算去除了原始图像内部的小孔(内部闭合的…...
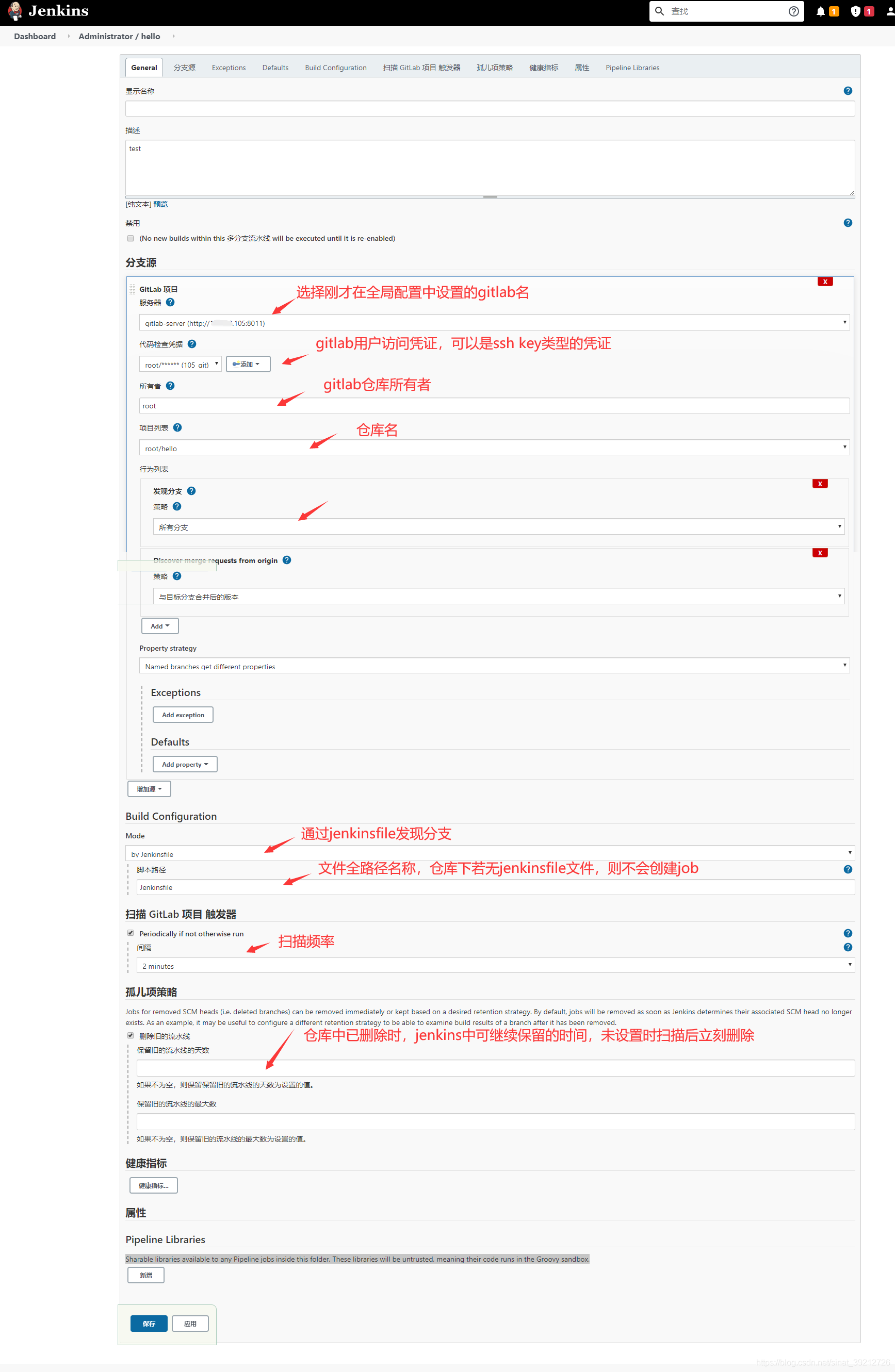
jenkins gitlab多分支构建发布
内容背景介绍 这个是新手教程,普及概念为主 公司现在还使用单分支发布测试环境和生产,多人协同开发同一个项目导致测试环境占用等待等情况 测试环境占用等待问题 测试环境代码直接合并到 master,容易导致误发布到生产的情况 避免多版本同时发布测试不完善的情况出现 中间件…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...

Docker、Wsl 打包迁移环境
电脑需要开启wsl2 可以使用wsl -v 查看当前的版本 wsl -v WSL 版本: 2.2.4.0 内核版本: 5.15.153.1-2 WSLg 版本: 1.0.61 MSRDC 版本: 1.2.5326 Direct3D 版本: 1.611.1-81528511 DXCore 版本: 10.0.2609…...
