【Codeforces】 CF468C Hack it!
题目链接
CF方向
Luogu方向
题目解法
令 ∑ i = 1 1 e 18 f ( i ) ≡ g ( g < a ) ( m o d a ) \sum_{i=1}^{1e18}f(i)\equiv g(g<a)(mod \;a) ∑i=11e18f(i)≡g(g<a)(moda)
那么 ∑ i = 2 1 e 18 + 1 f ( i ) ≡ g + 1 \sum_{i=2}^{1e18+1}f(i)\equiv g+1 ∑i=21e18+1f(i)≡g+1
同理 ∑ i = x 1 e 18 + x − 1 f ( i ) ≡ g + x − 1 \sum_{i=x}^{1e18+x-1}f(i)\equiv g+x-1 ∑i=x1e18+x−1f(i)≡g+x−1,其中 x < 1 e 18 x<1e18 x<1e18
考虑何时 g + x − 1 ≡ 0 g+x-1\equiv 0 g+x−1≡0
当 x x x 取 a − g + 1 a-g+1 a−g+1 时, ∑ i = a − g + 1 1 e 18 + a − g f ( i ) ≡ 0 ( m o d a ) \sum_{i=a-g+1}^{1e18+a-g}f(i)\equiv 0(mod\;a) ∑i=a−g+11e18+a−gf(i)≡0(moda)
所以 [ a − g + 1 , 1 e 18 + a − g ] [a-g+1,1e18+a-g] [a−g+1,1e18+a−g] 是一组合法的解
考虑求 g g g
每一位都可以从 0 0 0 取到 9 9 9,很好求, g = 18 ∗ 45 ∗ 1 0 17 + 1 = 81 ∗ 1 0 18 + 1 g=18*45*10^{17}+1=81*10^{18}+1 g=18∗45∗1017+1=81∗1018+1
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int mul=1e18;
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
signed main(){int a=read();int g_1=mul%a*9%a*9%a;printf("%lld %lld",a-g_1,mul+a-g_1-1);return 0;
}相关文章:

【Codeforces】 CF468C Hack it!
题目链接 CF方向 Luogu方向 题目解法 令 ∑ i 1 1 e 18 f ( i ) ≡ g ( g < a ) ( m o d a ) \sum_{i1}^{1e18}f(i)\equiv g(g<a)(mod \;a) ∑i11e18f(i)≡g(g<a)(moda) 那么 ∑ i 2 1 e 18 1 f ( i ) ≡ g 1 \sum_{i2}^{1e181}f(i)\equiv g1 ∑i21e181f…...
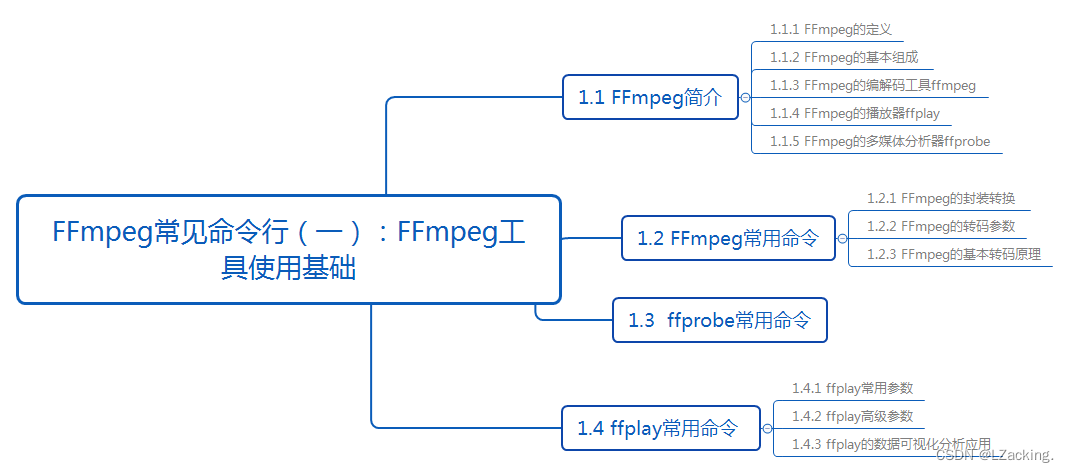
FFmpeg常见命令行(一):FFmpeg工具使用基础
前言 在Android音视频开发中,网上知识点过于零碎,自学起来难度非常大,不过音视频大牛Jhuster提出了《Android 音视频从入门到提高 - 任务列表》。本文是Android音视频任务列表的其中一个, 对应的要学习的内容是:FFmpe…...
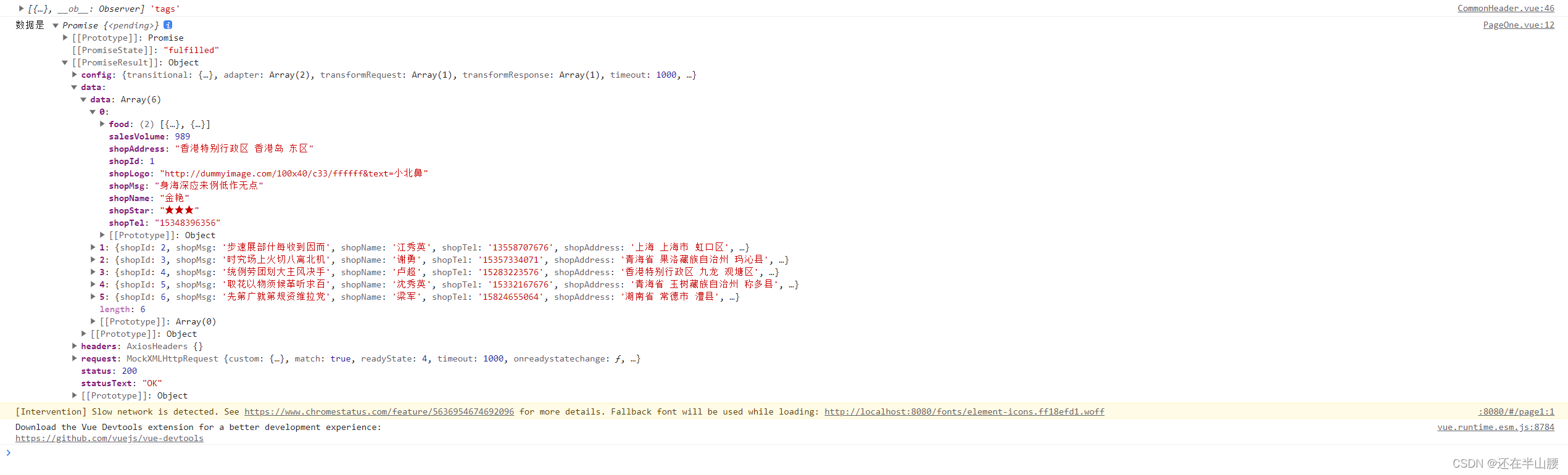
Mock.js的基本使用方法
官网网址:Mock.js (mockjs.com) 当前端工程师需要独立于后端并行开发时,后端接口还没有完成,那么前端怎么获取数据? 这时可以考虑前端搭建web server自己模拟假数据,这里我们选第三方库mockjs用来生成随机数据…...
TiDB 源码编译之 PD/TiDB Dashboard 篇
作者: ShawnYan 原文来源: https://tidb.net/blog/a16b1d46 TiDB TiDB 是 PingCAP 公司自主设计、研发的开源分布式关系型数据库,是一款同时支持在线事务处理与在线分析处理 (Hybrid Transactional and Analytical Processing, HTAP) 的融…...
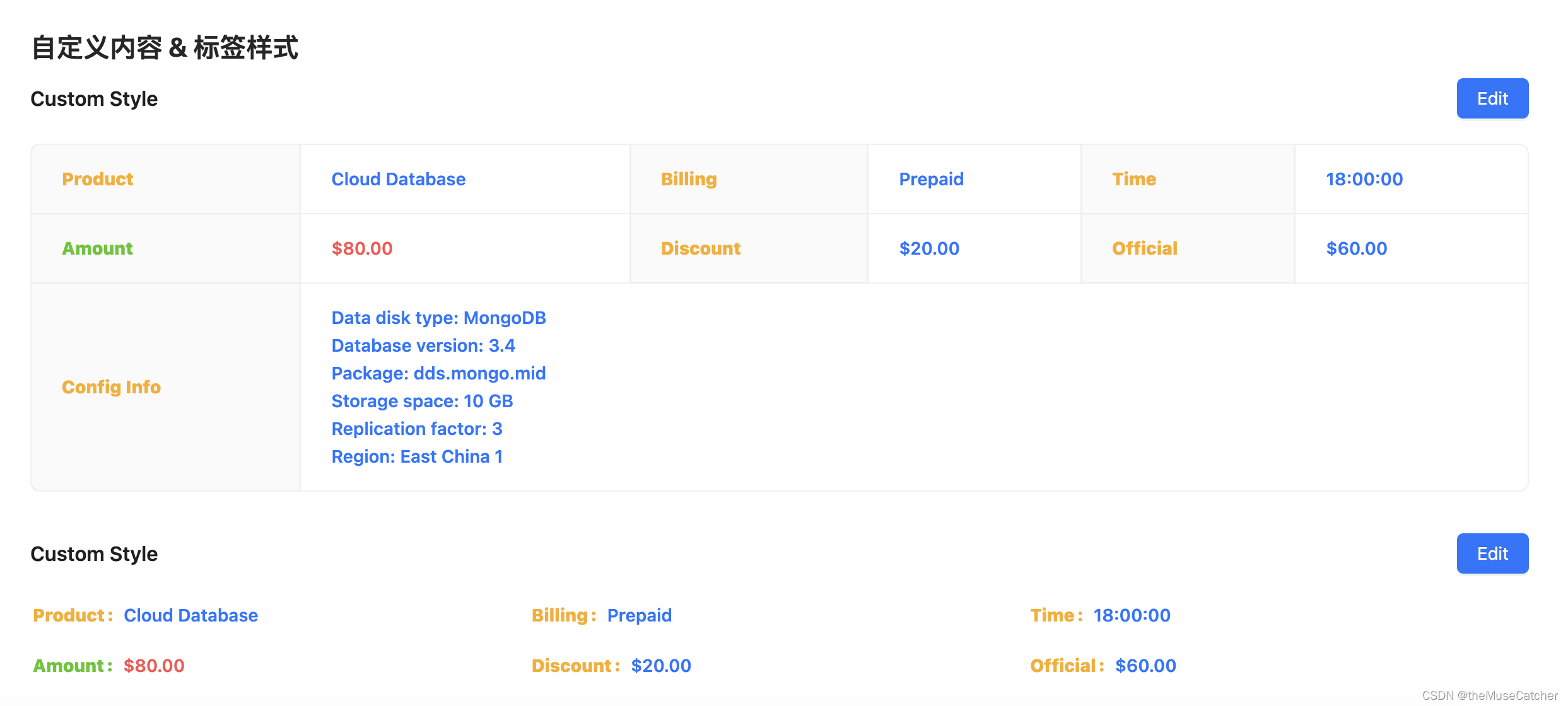
Vue3描述列表(Descriptions)
😁 整体功能效果与 ant design vue 保持高度一致 😁 包含两种组件:Descriptions 和 DescriptionsItem(必须搭配使用!) 效果如下图:在线预览 APIs Descriptions 参数说明类型默认值必传title…...
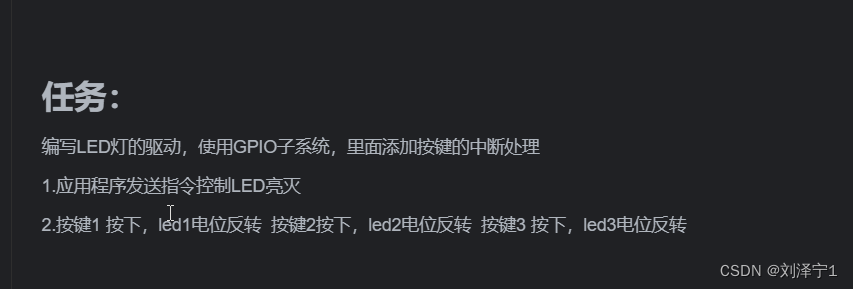
【驱动开发day8作业】
作业1: 应用层代码 #include <stdlib.h> #include <stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <unistd.h> #include <string.h> #include <sys/ioctl.h>int main(int…...

yxBUG记录
1、 原因:前端参数method方法名写错。 2、Field ‘REC_ID‘ doesn‘t have a default value 问题是id的生成问题。 项目的表不是自增。项目有封装好的方法。调用方法即可。 params.put("rec_id",getSequence("表名")) 3、sql语句有问题 检…...
uniapp引入inconfont自定义导航栏
app,h5端引入 uniapp本身的全局设置中有个iconfontsrc属性 所以只需要 1.iconfont将需要的icon添加至项目 2.下载到本地解压后,将其中的ttf文件,放在static静态目录下 3.在page.json中对全局文件进行配置tabBar(导航图标) “iconfontSrc”: “static/font/iconfont.ttf”, …...
OSLog与NSLog对比
NSLog: NSLog的文档,第一句话就说:Logs an error message to the Apple System Log facility.,所以首先,NSLog就不是设计作为普通的debug log的,而是error log;其次,NSLog也并非是printf的简单…...
全网最细,Fiddler修改接口返回数据详细步骤实战,辅助接口测试...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 在测试的过程中&a…...
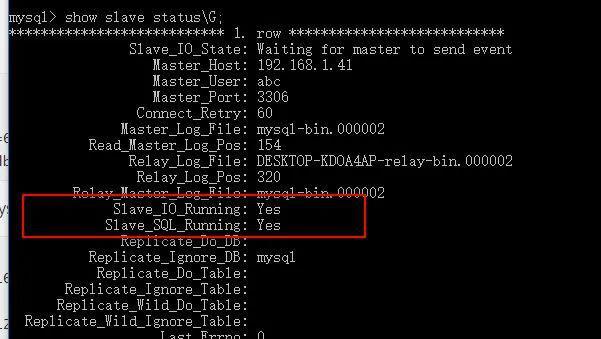
Mysql自动同步的详细设置步骤
以下步骤是真实的测试过程,将其记录下来,与大家共同学习。 一、环境说明: 1、主数据库: (1)操作系统:安装在虚拟机中的CentOS Linux release 7.4.1708 (Core) [rootlocalhost ~]# cat /etc/redh…...
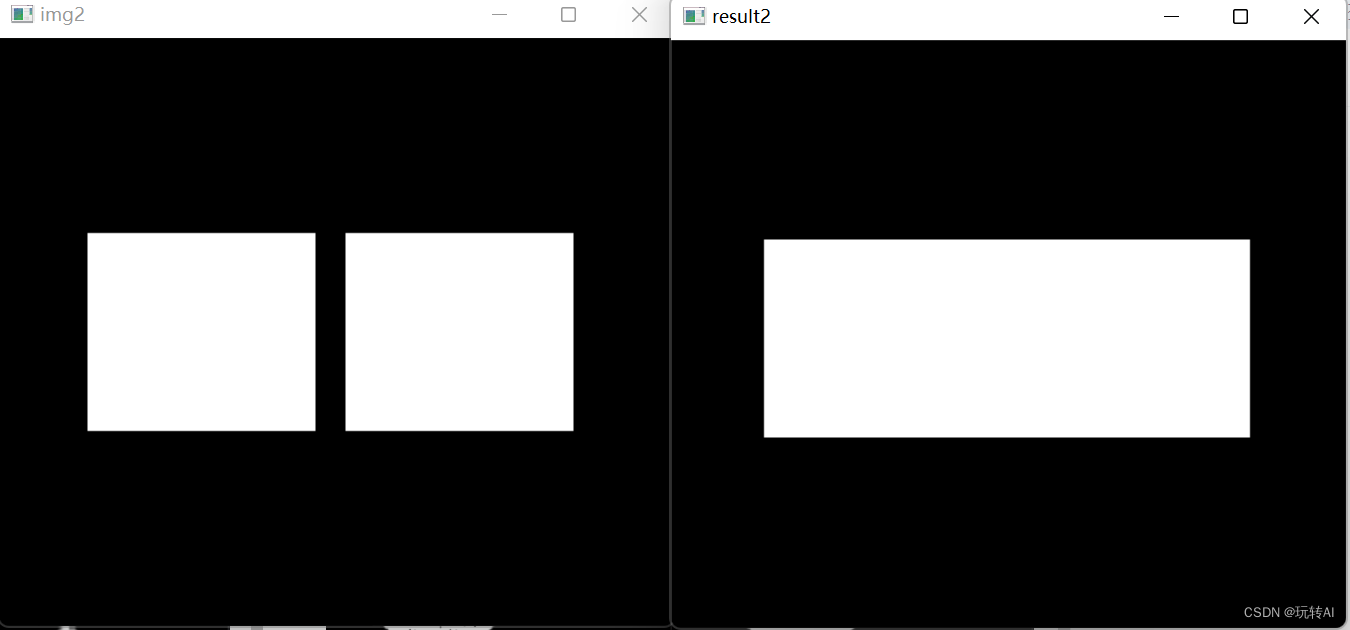
opencv-38 形态学操作-闭运算(先膨胀,后腐蚀)cv2.morphologyEx(img, cv2.MORPH_CLOSE, kernel)
闭运算是先膨胀、后腐蚀的运算,它有助于关闭前景物体内部的小孔,或去除物体上的小黑点,还可以将不同的前景图像进行连接。 例如,在图 8-17 中,通过先膨胀后腐蚀的闭运算去除了原始图像内部的小孔(内部闭合的…...
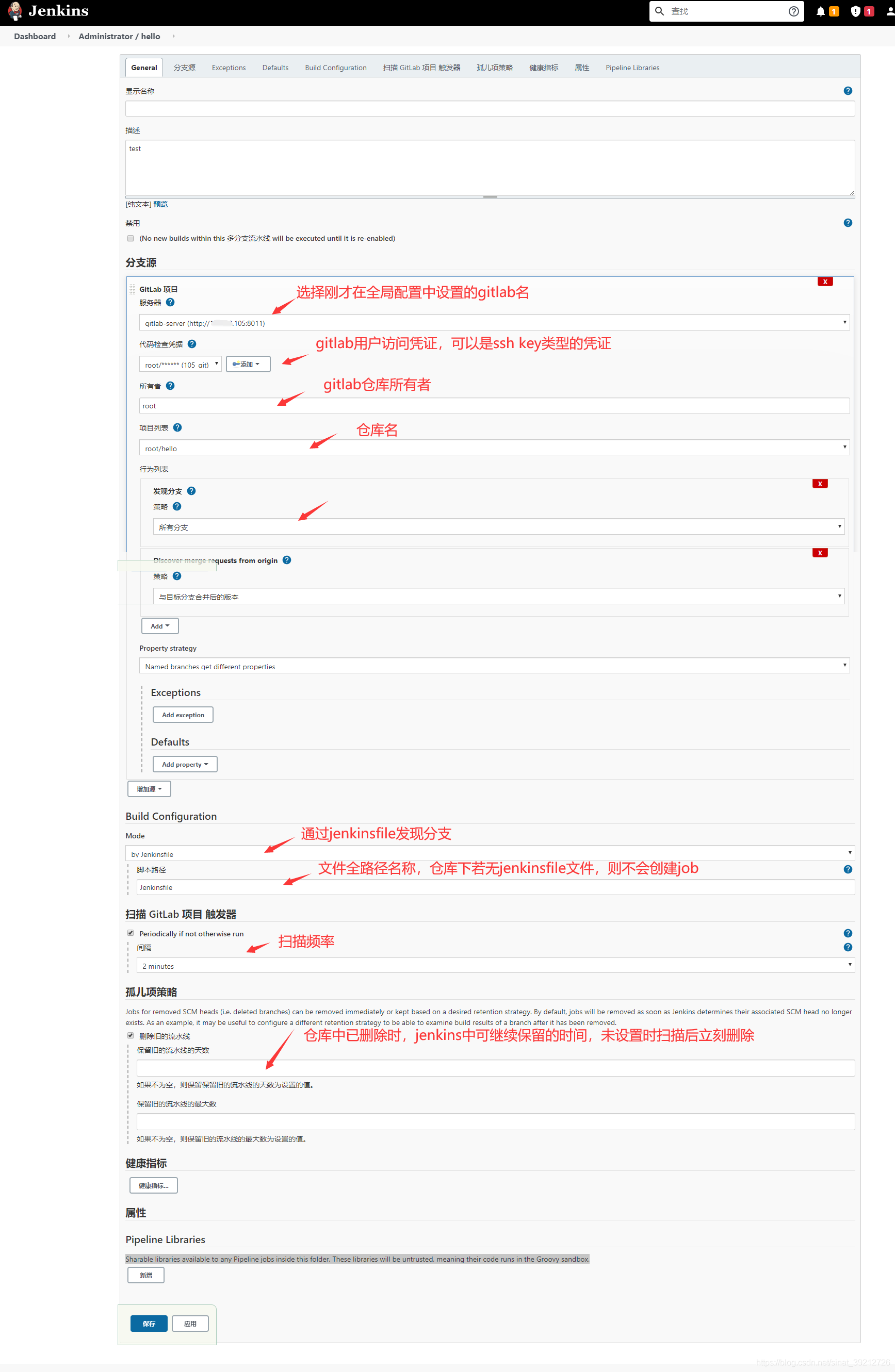
jenkins gitlab多分支构建发布
内容背景介绍 这个是新手教程,普及概念为主 公司现在还使用单分支发布测试环境和生产,多人协同开发同一个项目导致测试环境占用等待等情况 测试环境占用等待问题 测试环境代码直接合并到 master,容易导致误发布到生产的情况 避免多版本同时发布测试不完善的情况出现 中间件…...
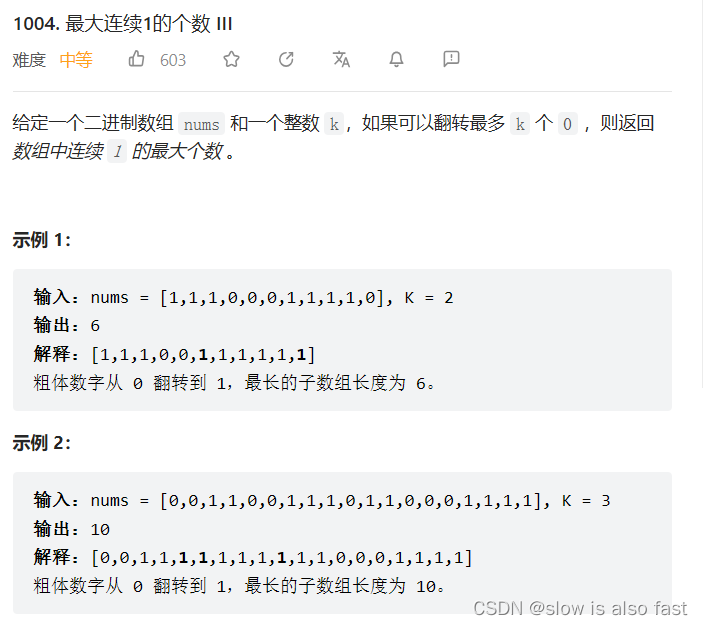
刷题笔记 day8
1004 最大连续1的个数 III 这道题要求将原数组中的0翻转成1,求出最大元素全是1的子数组长度,看这道题第一感觉还要将里面的0变成1,感觉这道题解决起来很麻烦,但是我们可以转变思路,找出其最大子数组,使得子…...

C 语言的表达式
表达式 expression 表达式由运算符和运算对象组成。 最简单的表达式是一个单独的运算对象,以此为基础可以建立复杂的表达式。 一些表达式由子表达式(subexpression)组成。子表达式即较小的表达式。 这些都是一些表达式: -4 a…...

C++设计模式创建型之单例模式
一、概述 单例模式也称单态模式,是一种创建型模式,用于创建只能产生一个对象实例的类。例如,项目中只存在一个声音管理系统、一个配置系统、一个文件管理系统、一个日志系统等,甚至如果吧整个Windows操作系统看成一个项目…...

杂记 | 记录一次使用Docker安装gitlab-ce的过程(含配置交换内存)
文章目录 01 准备工作02 (可选)配置交换内存03 编辑docker-compose.yml04 启动并修改配置05 nginx反向代理06 (可选)修改配置文件07 访问并登录 01 准备工作 最近想自建一个gitlab服务来保存自己的项目,于是找到gitla…...

MyBatis@Param注解的用法
一、前言 本人在学习mybatis的过程中遇到的一个让人不爽的bug,在查找了些相关的资料后得以解决,遂记录。 二、报错及解决 mapper中有一方法: Select("select * from emp " "where name like concat(%, #{name}, %) "…...
Shader 编程:GLSL 重要的内置函数
该原创文章首发于微信公众号:字节流动 未经作者(微信ID:Byte-Flow)允许,禁止转载 前面发了一些关于 Shader 编程的文章,有读者反馈太碎片化了,希望这里能整理出来一个系列,方便系统的…...

浏览器同源策略
浏览器同源策略 同源策略:是一个重要的浏览器的安全策略,用于限制一个源的文档或者它加载的脚本如何能与另一个源的资源进行交互 它能帮助阻隔恶意文档,减少可能被攻击的媒介 例如:被钓鱼网站收集信息,使用ajax发起…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

Python爬虫(52)Scrapy-Redis分布式爬虫架构实战:IP代理池深度集成与跨地域数据采集
目录 一、引言:当爬虫遭遇"地域封锁"二、背景解析:分布式爬虫的两大技术挑战1. 传统Scrapy架构的局限性2. 地域限制的三种典型表现 三、架构设计:Scrapy-Redis 代理池的协同机制1. 分布式架构拓扑图2. 核心组件协同流程 四、技术实…...

AI书签管理工具开发全记录(十八):书签导入导出
文章目录 AI书签管理工具开发全记录(十八):书签导入导出1.前言 📝2.书签结构分析 📖3.书签示例 📑4.书签文件结构定义描述 🔣4.1. 整体文档结构4.2. 核心元素类型4.3. 层级关系4.…...
进行稀疏数据预测的技术方案)
结合PDE反应扩散方程与物理信息神经网络(PINN)进行稀疏数据预测的技术方案
以下是一个结合PDE反应扩散方程与物理信息神经网络(PINN)进行稀疏数据预测的技术方案,包含完整数学推导、PyTorch/TensorFlow双框架实现代码及对比实验分析。 基于PINN的反应扩散方程稀疏数据预测与大规模数据泛化能力研究 1. 问题定义与数学模型 1.1 反应扩散方程 考虑标…...
