QT 使用单例模式
目录
1. 单例模式介绍
2.单例模式实现

1. 单例模式介绍
有些时候我们在做 qt 项目的时候,要用到很多类. 例如我们用到的类有 A,B,C,D. 其中,A 是 B,C,D 中都需要用到的类,A 类非常的抢手. 但是,A 类非常的占内存,定义一个 A 对象需要 500M 内存,假如在 B,C,D 中都定义一个 A 类对象,对 内存的消耗是可想而知的.
所以 B,C,D 分别都定义一个 A 类对象是不可能的. 那么我们此时就希望: 能不能把 A 定义成"全局变量",然后这样子 B,C,D 类都能访问,并且整个程序就只有这一个 A?
答案是可以的,定义 A 的时候以单例模式定义即可
单例模式作为一种常用的软件设计模式,主要是用来保证系统中只有一个实例,例如一般一个程序中只有一 个日志输出实例,一个系统中只有一个数据库连接实例,这时候用单例模式非常合适。
单例模式用来做什么
正如之前所说,单例模式:
(1) 整个程序只有一个对象;
(2) 整个程序都能访问到它;
(3) 分为"懒汉模式"和"饿汉模式";
(4) "懒汉模式"是用到单例的时候才创建,否则不创建对象;
(5) "饿汉模式"是在程序启动时就需要创建变量;
懒汉模式是时间换空间,饿汉模式是空间换时间。
单例模式是在大型项目用到非常多的,例如:
(1) 一个日记记录类,必须整个程序只能有一个,假如有 2 个,在写日志文件时会相互"践踏".
(2) 数据库操作,连接类,必须整个程序只能有一个,假如有 2 个就会出问题,你想看假如 2 个进程同时使用 同一个账号,然后写入同一个数据会发生什么事情...
单例模式有效的解决了重复定义对象的问题,假如配合互斥锁,还可以解决多进程,线程之间的同步互斥问题, 也就是同一时间只能有一个进程操作单例对象。
2.单例模式实现
设计单例模式非常简单:
cpp文件实例:
//这句一定要写,因为 self 是静态变量,必须要初始化值
ClassA* ClassA::self = NULL;
ClassA *ClassA::getInstance()
{//判断是否是第一次调用//假如不为 NULL,会直接 returnif (self == NULL) {//防止多进程同时调用创建 2 个对象的问题//原理是因为是静态变量只会定义一次static QMutex mutex;//上锁QMutexLocker locker(&mutex);//在判断一次,防止其它进程抢先 new 过了if (self == NULL) {self = new ClassA;}}return self; //返回指针
}h头文件实例:
class ClassA : public QObject
{Q_OBJECT
public://通过它获取 self 指针,这个函数是静态调用,不需要创建对象就可以访问static ClassA *getInstance(); //返回自身的指针//构造函数explicit ClassA(QObject *parent = 0);void hello(){ //一个普通函数qDebug() << "hello world";}
private:static ClassA *self; //静态指针
};
#endif // ICONFONT_H在其他类里的调用方法:
ClassA::getInstance()->hello();
其中:
ClassA::getInstance()会获取全局的 self 指针,通过这个指针我们可以访问到里边的函数。在任何类里,都可以 无条件访问 A 对象,并且不需要创建 A 对象,而且 A 对象全局只有一个实例:
(1) 在类 A 里定义一个静态的指针 self;
(2) 当调用获取 A 对象的指针时,判断这个 self 是否为空,假如为空则创建新对象并赋值给 self 并返回 self,存 在则直接返回 self;
在此使用用的最多的"懒汉模式"进行演示:
cpp 代码如下(以数据库为例(多个 ui 界面都使用到此类)):
#include "qmqttclient.h"
#include <QMutex>
#include <QMutexLocker>
#include <QMessageBox>
//构造函数
QmqttClient::QmqttClient()
{}
//这句一定要写,因为 self 是静态变量,必须要初始化值
QmqttClient* QmqttClient::mqttSelf = NULL;
QmqttClient *QmqttClient::getInstance()
{//判断是否是第一次调用//假如不为 NULL,会直接 returnif (mqttSelf == NULL) {//防止多进程同时调用创建 2 个对象的问题//原理是因为是静态变量只会定义一次static QMutex mutex;//上锁 QMutexLocker 会锁住 mutex,当 QMutexLocker 被释放的时候自动解锁//locker 是局部变量,所以 getInstance 函数结束时会自动解锁QMutexLocker locker(&mutex);//在判断一次,防止其它进程抢先 new 过了if (mqttSelf == NULL) {mqttSelf = new QmqttClient;}}return mqttSelf; //返回指针
}
头文件
#ifndef QMQTTCLIENT_H
#define QMQTTCLIENT_H
#include <QObject>
#include "qmqtt.h"
#include <QtCore>
class QmqttClient : public QObject{Q_OBJECT
public://通过它获取 self 指针,这个函数是静态调用,不需要创建对像就可以访问,函数名
自定义//这个函数的作用是给别人获取它的静态对象 返回自身的指针static QmqttClient *getInstance();
// void hello(){ //一个普通函数
// qDebug() << "hello world";
private:QmqttClient(); //构造函数,写在 private 下,不允许 new 生成单例static QmqttClient *mqttSelf;//静态指针
};
在其他类里的调用方法:
QmqttClient::getInstance()->mqttClient->setHost(ui->lEditServerIP->text()); //服务 器 IP QmqttClient::getInstance()->mqttClient->setPort(1883);//端口号
其中: QmqttClient::getInstance()会获取全局的 self 指针,通过这个指针我们可以访问到里边的函数. 在任何类里,都可以无条件访问 A 对象,并且不需要创建 A 对象,而且 A 对象全局只有一个实例: 注意:可以把多个对象放到单例模式
相关文章:

QT 使用单例模式
目录 1. 单例模式介绍 2.单例模式实现 1. 单例模式介绍 有些时候我们在做 qt 项目的时候,要用到很多类. 例如我们用到的类有 A,B,C,D. 其中,A 是 B,C,D 中都需要用到的类,A 类非常的抢手. 但是,A 类非常的占内存,定义一个 A 对象需要 500M 内存,假如在 B,C,D 中都定义一个 A 类…...

接口测试——postman接口测试(三)
目录 1. postman介绍与安装 2. postman发送get请求 3. postman发送post请求 1. postman介绍与安装 安装网址:Postman安装教程:留言找我要即可 2. postman发送get请求 import pymysql from flask import Flask,request# 这里是mysql的基本连接信息 c…...
react中hooks的理解与使用
一、作用 我们知道react组件有两种写法一种是类组件,另一种是函数组件。而函数组件是无状态组件,如果我们要想改变组件中的状态就无法实现了。为此,在react16.8版本后官方推出hooks,用于函数组件更改状态。 二、常用API 1、use…...
STM32的电动自行车信息采集上报系统(学习)
摘要 针对电动自行车实时监管不便的问题,设计了一种基于STM32的电动自行车信息采集系统,通过获取电池、位置和行驶状态信息并上报到服务器中,实现实时监管。 通过多路串口请求电池、行驶状态和位置信息,以并发方式进行数据接收、…...
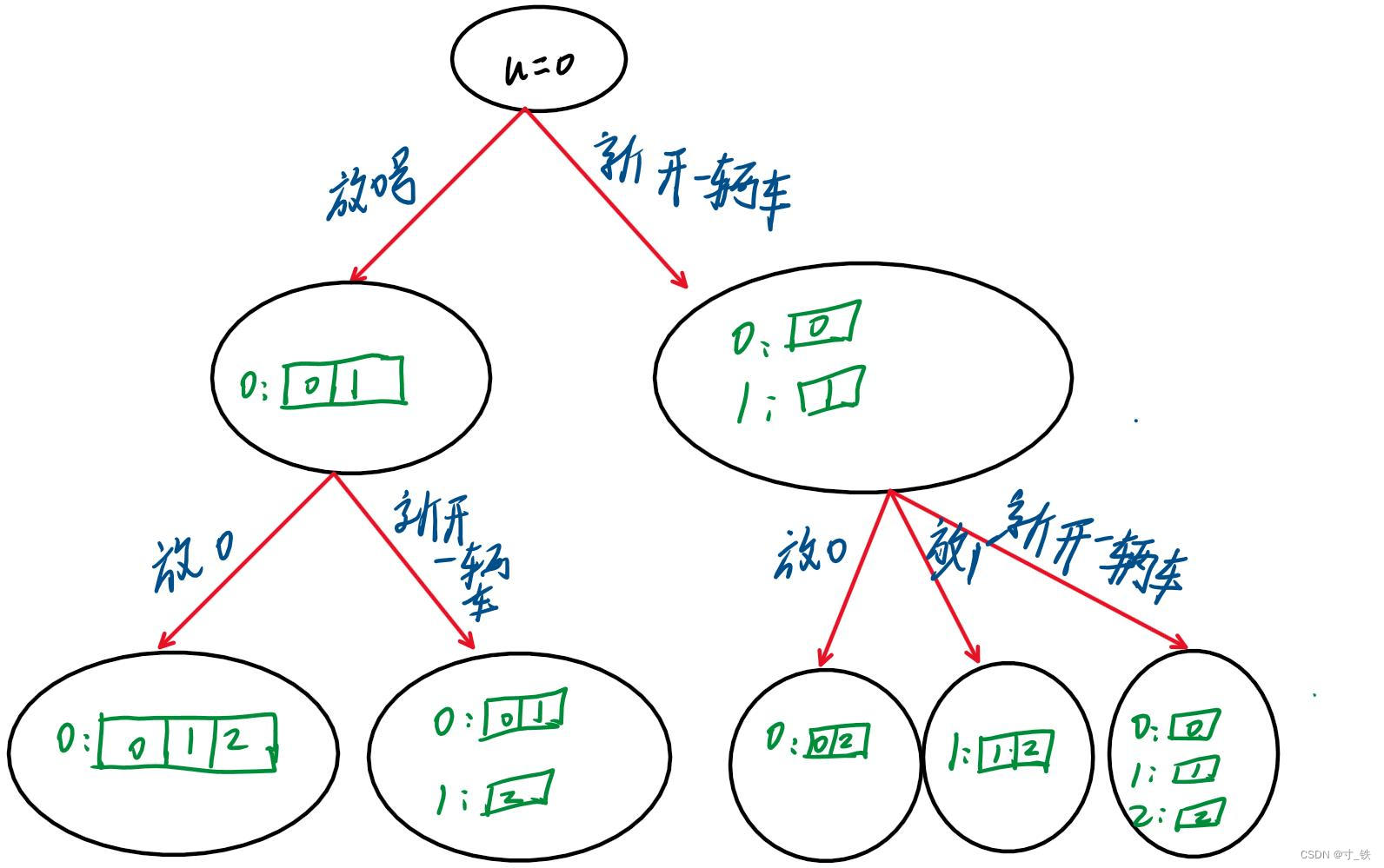
蓝桥杯上岸每日N题 第七期(小猫爬山)!!!
蓝桥杯上岸每日N题 第七期(小猫爬山)!!! 同步收录 👇 蓝桥杯上岸必背!!!(第四期DFS) 大家好 我是寸铁💪 冲刺蓝桥杯省一模板大全来啦 🔥 蓝桥杯4月8号就要开始了 &a…...
【Linux系统编程】冯诺依曼体系结构
目录 前言 什么是冯诺依曼体系结构? 冯诺依曼体系结构如何进行数据处理的? 存储器在冯诺依曼体系中有什么作用? 冯诺依曼体系结构为什么要这样设计? 冯诺依曼结构总结 前言 相信对于冯诺依曼这个人的名字大家一定不会感到陌…...
数据结构--动态顺序表
文章目录 线性表动态顺序表数组与顺序表 接口实现初始化:尾插:尾删头插头删指定位置插入指定位置删除查找摧毁 完整代码 线性表 线性表是数据结构中最基本、最简单也是最常用的一种数据结构。线性表是指由n个具有相同数据类型的元素组成的有限序列。 线…...
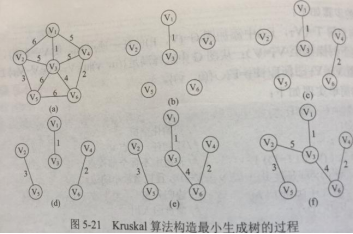
笔试数据结构选填题
目录 卡特兰数Catalan:出栈序列/二叉树数 树 二叉树 N01N2 哈夫曼树(最优二叉树)Huffman 度m的哈夫曼树只有度为0和m的结点:Nm(n-1)/(m-1) 平衡二叉树AVL Nh表示深度为h最少结点数,则N00,N11&#…...

# 鸢尾花的案例学习
# 鸢尾花的案例学习 # 1. 导入小型的数据 from sklearn.datasets import load_iris import numpy as np import pandas as pd import seaborn as sbn import matplotlib.pyplot as plt # 2. 获取数据 irisload_iris() # 3.查看数据print("数据集\n ",len(iris.d…...

线程、进程的区别
线程、进程的区别 在开发中,我们经常听到线程和进程两个概念,它们都是操作系统的基本概念,操作系统以进程为基本单位分配存储器,以线程为基本单位分配CPU。虽然它们有很多相似之处,但是它们也有很大的区别。本文将详细…...

在 Ubuntu 上安装 Docker 桌面
Ubuntu 22.04 (LTS) 安装 Docker 桌面 要成功安装 Docker Desktop,您必须: 满足系统要求拥有 64 位版本的 Ubuntu Jammy Jellyfish 22.04 (LTS) 或 Ubuntu Impish Indri 21.10。对于非 Gnome 桌面环境,必须安装 gnome-terminal:…...
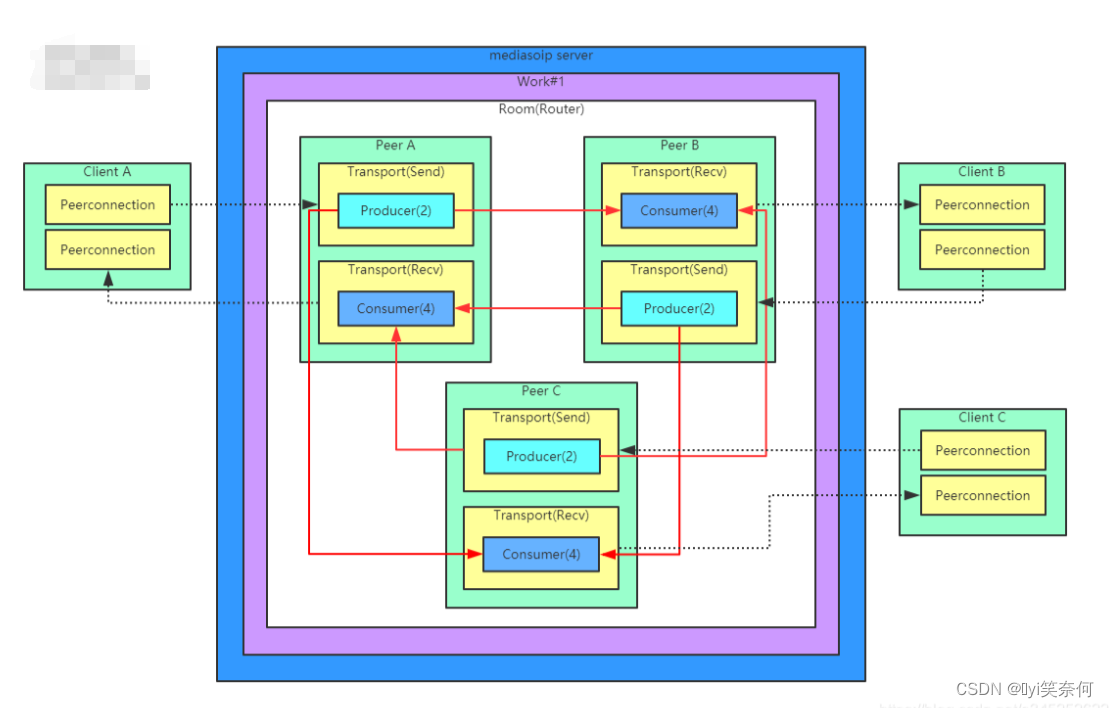
【WebRTC---序篇】(七)RTC多人连麦方案
服务端可以选择mediasoup,作为SFU服务器,只负责转发数据 下图举例三个Client (browser或者客户端)同时加入一个房间,每个app同时发布一路视频和一路音频,并且接受来自其他app的音视频流,mediasoup内部的结构如下&…...

【Java可执行命令】(十六)诊断命令请求发送工具 jcmd:提供一种简单而强大的方式来管理和监控 Java 进程 ~
Java可执行命令之jcmd 1️⃣ 概念2️⃣ 优势和缺点3️⃣ 使用3.1 语法格式3.2 jcmd -l:列出正在运行的 Java 进程3.3 jcmd < pid> help:列出特定进程的诊断命令列表3.4 jcmd < pid> < command>:执行诊断命令 4️⃣ 应用场景…...

如何创建无序列表和有序列表?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 无序列表⭐ 无序列表⭐ 注意事项⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴…...
【MongoDB】初识、安装MongoDB
目录 一、MongoDB主要应用场景 二、MongoDB简介 三、MongoDB相关特点 四、MongoDB的安装 一、MongoDB主要应用场景 传统的数据库如MySQL在应对三高场景时显得力不从心 三高: High performance 对数据库高并发读写的需求 High Storage 对海量数据的高效率存储和 …...
方法区内存溢出及常量池
22 方法区-定义 是所有线程共享的一块区域。 存储了和类结构相关信息。运行时常量池, 方法区在虚拟机启动时被创建,逻辑上是堆的组成部分。方法区内存不足,也会导致oom异常。 是一个概念上的东西, 1.6使用永久代作为方法区&#…...

【MTK平台】【wpa_supplicant】关于wpa_supplicant_8/src/p2p/p2p_invitation.c文件的介绍
本文主要介绍external/wpa_supplicant_8/src/p2p/p2p_invitation.c文件 这里主要介绍6个方法 1.p2p_invite //p2p邀请调用此方法 2.p2p_invite_send //对p2p_invite方法进行补充 3. p2p_process_invitation_resp 4.p2p_process_invitation_req 5.p2p_build_invitation_re…...
智能仪表板DevExpress Dashboard v23.1亮点 - 增强对自定义导出的支持
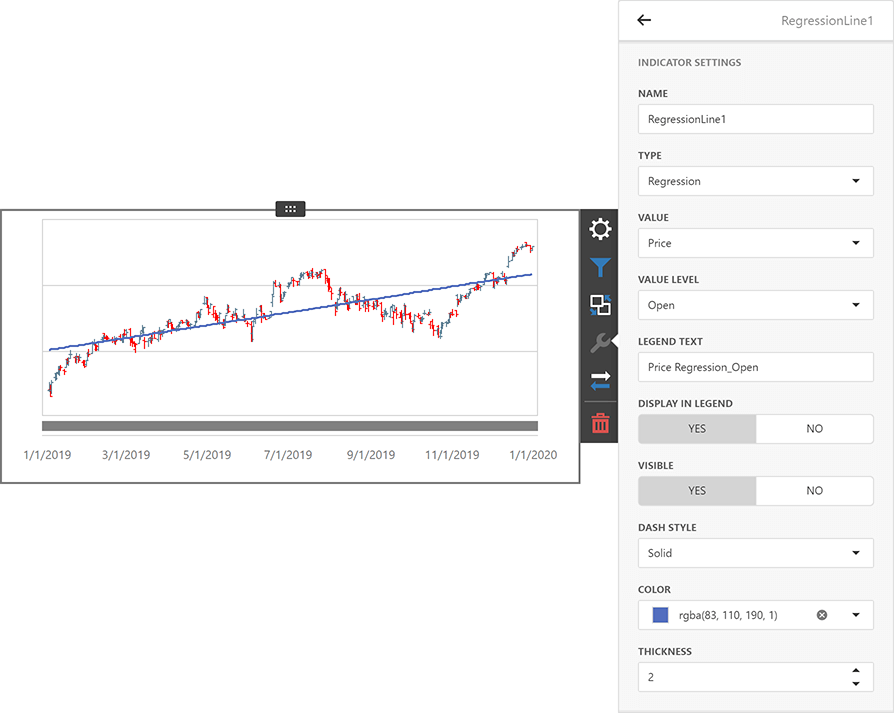
DevExpress Dashboard v23.1版本增强了自定义导出到Excel的功能等,欢迎下载最新版本体验! DevExpress Dashboard v23.1正式版下载(Q技术交流:523159565) 所有平台 导出自定义仪表板项目到Excel 用户现在可以在WinForms和Web应…...

分布式应用:ELK企业级日志分析系统
目录 一、理论 1.ELK 2.ELK场景 3.完整日志系统基本特征 4.ELK 的工作原理 5.ELK集群准备 6.Elasticsearch部署(在Node1、Node2节点上操作) 7.Logstash 部署(在 Apache 节点上操作) 8.Kiabana 部署(在 Node1 节点…...
Mac与windows传文件(超过4G且速度超快,非共享)
MAC与Windows文件互传 背景 尝试了网上的一些方法,诸如设置共享文件夹方法等,但是实际使用中感觉效果一般,对于一些小的文件共同编辑速度还可以。但是在备份或者传递一些较大文件或者很多细小文件的时候就有点捉襟见肘了。制作了一个MAC可读…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
