手写一个简易的布隆过滤器
1.什么是布隆过滤器
布隆过滤器(Bloom Filter)是1970年由布隆(人名)提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都比一般的算法要好的多,缺点是有一定的误识别率和删除困难。
人话理解就是,布隆过滤器是一个容器,我们可以往这个容器里添加元素,并且可以查询某个元素是否在容器中存在,欸有人就经验的可以知道,这个工作Set也可以做,为什么要用布隆过滤器呢,
- 布隆过滤器的优点:
时间复杂度低,增加和查询元素的时间复杂为O(N),(N为哈希函数的个数,通常情况比较小)
保密性强,布隆过滤器不存储元素本身
占用空间小,如果允许存在一定的误判,布隆过滤器是非常节省空间的(相比其他数据结构如Set集合) - 布隆过滤器的缺点:
有点一定的误判率,但是可以通过调整参数来降低
无法获取元素本身
很难删除元素(可以试试自己实现一个可以删除元素的某隆过滤器)
2. 布隆过滤器的使用使用场景
布隆过滤器可以告诉我们 “某样东西一定不存在或者可能存在”,也就是说布隆过滤器说这个数不存在则一定不存,布隆过滤器说这个数存在可能不存在(误判,后续会讲),**利用这个判断是否存在的特点可以做很多有趣的事情。
- 解决Redis缓存穿透问题(面试重点)
- 邮件过滤,使用布隆过滤器来做邮件黑名单过滤
- 对爬虫网址进行过滤,爬过的不再爬
- 解决新闻推荐过的不再推荐(类似抖音刷过的往下滑动不再刷到)
- HBase\RocksDB\LevelDB等数据库内置布隆过滤器,用于判断数据是否存在,可以减少数据库的IO请求
实现原理
布隆过滤器它实际上是一个很长的二进制向量和一系列随机映射函数。以Redis中的布隆过滤器实现为例,Redis中的布隆过滤器底层是一个大型位数组(二进制数组)+多个无偏hash函数。
我下面的实现是采用了二维数组的方式来实现的,一个hash函数对应每一个数组,这样的误判率会非常小,当然每个人都有自己的实现方式,学习思想即可
代码实现
1.定义接口
public interface AccessInterface<T extends Object> {void add(T t);boolean query(T t);boolean set(T t);
}
2.hash值方法实现
public class HashCode<T extends Object> {/*** @param index* @param length* @param t* @return* 注:适用于hashpool较小的时候,,太大了不行。计算hash值的时候会溢出,当然这个问题换个对象来计算就行了,这里图省事就简单点, Java有内置的大数据对象。*/public int GetHashCode(int index,int length,T t){int hashcode=t.hashCode();Long hashcode1=Math.round(Math.floor((hashcode+index+index*index)%length));return hashcode1.intValue();}}
- 过滤器实现
/*** 过滤器实现*/
public class BlloomEnity<T extends Object> implements AccessInterface<T> {private boolean[][] blloompool;private int length;HashCode<T> Code;public BlloomEnity() {this.length=100;this.blloompool=new boolean[100][100];this.Code=new HashCode<T>();}public BlloomEnity( int length) {this.blloompool = new boolean[length][length];this.length = length;this.Code=new HashCode<T>();}@Overridepublic void add(T o) {for(int i=0;i<this.length;i++){int k=Code.GetHashCode(i+1,this.length,o);this.blloompool[i][k]=true;}}@Overridepublic boolean query(T o) {for(int i=0;i<this.length;i++){int k=Code.GetHashCode(i+1,this.length,o);if(!this.blloompool[i][k]){return false;}}return true;}@Overridepublic boolean set(T o) {if(query(o)){return false;}else{add(o);}return true;}
}
- 测试
完事儿,一切对象都可存,
相关文章:

手写一个简易的布隆过滤器
1.什么是布隆过滤器 布隆过滤器(Bloom Filter)是1970年由布隆(人名)提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都比一般的算法要好的多,…...

阿里云快速部署开发环境 (Apache + Mysql8.0)
本文章的内容截取于云服务器管理控制台提供的安装步骤,再整合前人思路而成,文章末端会提供原文连接 ApacheMysql 8.0部署MySQL数据库(Linux)步骤一:安装MySQL步骤二:配置MySQL步骤三:远程访问My…...

侧边栏的打开与收起
侧边栏的打开与收起 <template><div class"box"><div class"sideBar" :class"showBox ? : controller-box-hide"><div class"showBnt" click"showBox!showBox"><i class"el-icon-arrow-r…...

贝叶斯学习
贝叶斯 贝叶斯学习的背景贝叶斯定理举例 概览选择假设— MAPMAP举例 选择假设 — 极大似然 MLML 举例: 抛硬币问题 极大似然 & 最小二乘Nave Bayesian Classifier (朴素贝叶斯分类器)举例1:词义消歧 (Word Sense Disambiguation)举例 2: 垃圾邮件过滤 从垃圾邮件…...

Java并发系列之六:CountDownLatch
CountDownLatch作为开发中最常用的组件,今天我们来聊聊它的作用以及内部构造。 首先尝试用一句话对CountDownLatch进行概括: CountDownLatch基于AQS,它实现了闩锁,在开发中可以将其用作任务计数器。 若想要较为系统地去理解这些特性ÿ…...

24数据结构-图的基本概念与存储结构
目录 第六章 图6.1 图的基本概念知识回顾 6.2 图的储存结构(邻接矩阵法)1. 数组表示法(1) 有向图,无向图的邻接矩阵 2. 定义邻接矩阵的结构3. 定义图的结构4. 构造图G5. 特点 第六章 图 6.1 图的基本概念 图是一种非线性结构 图的特点&am…...
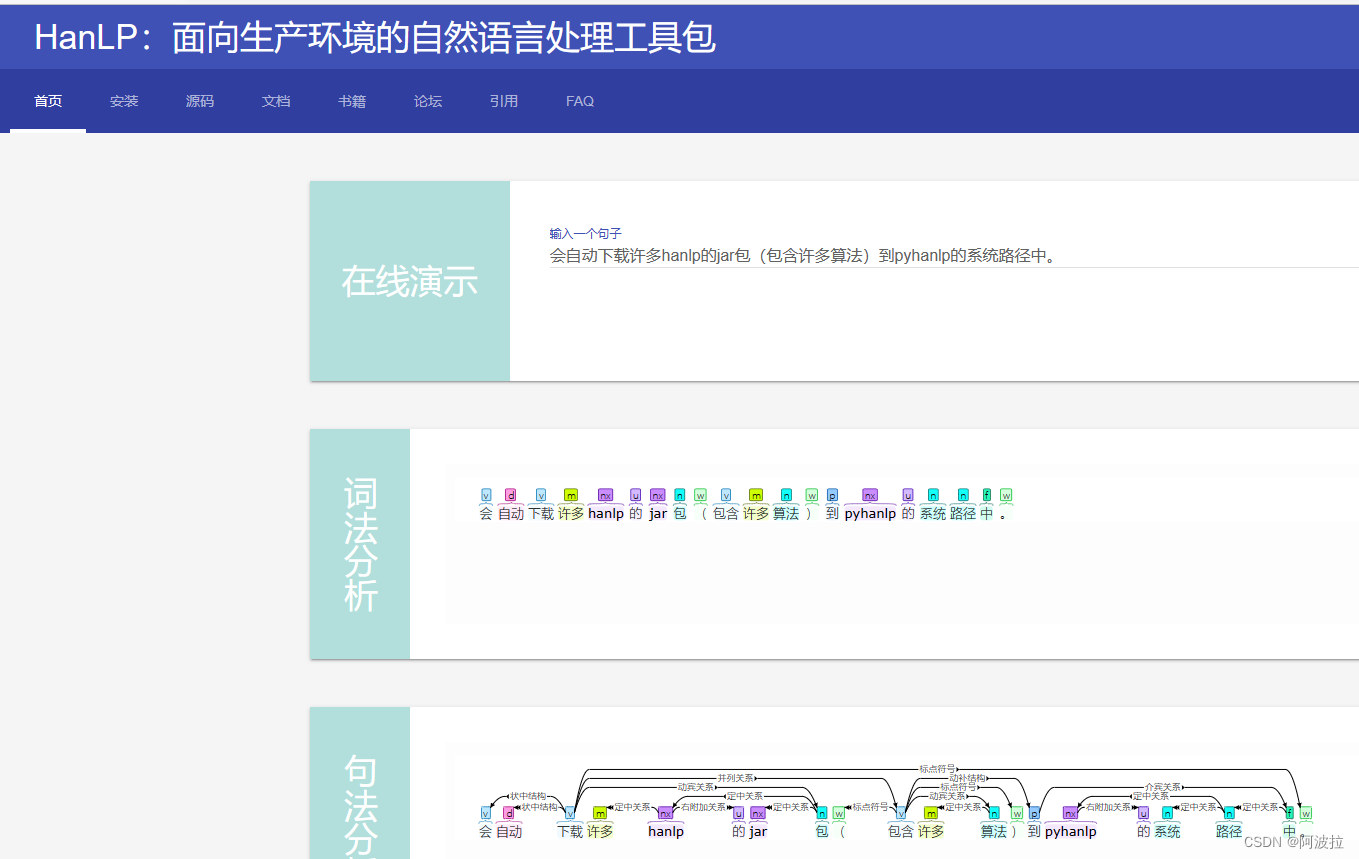
自然语言处理学习笔记(三)————HanLP安装与使用
目录 1.HanLP安装 2.HanLP使用 (1)预下载 (2)测试 (3)命令行 (4)测试样例 3.pyhanlp可视化 4. HanLP词性表 1.HanLP安装 HanLP的 Python接口由 pyhanlp包提供,其安装…...
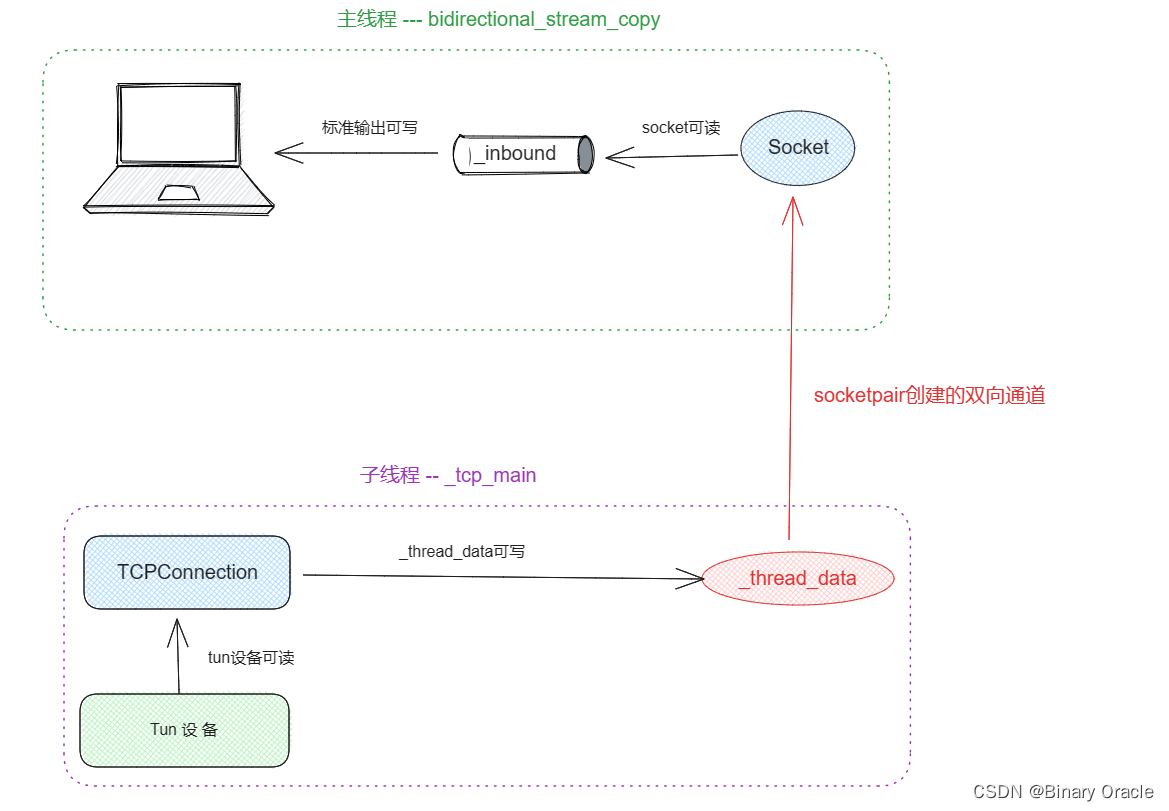
CS 144 Lab Five -- the network interface
CS 144 Lab Five -- the network interface TCP报文的数据传输方式地址解析协议 ARPARP攻击科普 Network Interface 具体实现测试tcp_ip_ethernet.ccTCPOverIPv4OverEthernetAdapterTCPOverIPv4OverEthernetSpongeSocket通信过程 对应课程视频: 【计算机网络】 斯坦福大学CS144…...

Mecha
一、Mecha Mecha 是一个开源的多云 Kubernetes 管理平台,旨在简化和统一在多个云提供商上运行 Kubernetes 集群的管理和操作。它是由阿里巴巴集团开发和维护的项目。 Mecha 的主要目标是提供一个统一的界面和工具,使用户能够更轻松地在不同的云提供商上…...

Apache RocketMQ之集成RocketMQ_MQTT 安装部署协议
Apache RocketMQ 安装说明 安装步骤 参考快速开始 https://rocketmq.apache.org/zh/docs/quickStart/01quickstart 安装可视化rocketmq_dashboard下载地址 https://rocketmq.apache.org/zh/docs/4.x/deployment/03Dashboard/ 安装rocketmq_mqtt https://rocketmq.apache.o…...

Oracle多行数据合并为一行数据,并将列数据转为字段名
Oracle多行数据合并为一行数据 实现查询效果原数据 方式一:MAX()数据效果SQL 方式二:LISTAGG()数据效果 方式三:WM_CONCAT()数据效果 实现查询效果 原数据 FZPROJECTVALUE1电脑$16001手机$121导管$12电脑$22手机$22 方式一:MAX…...
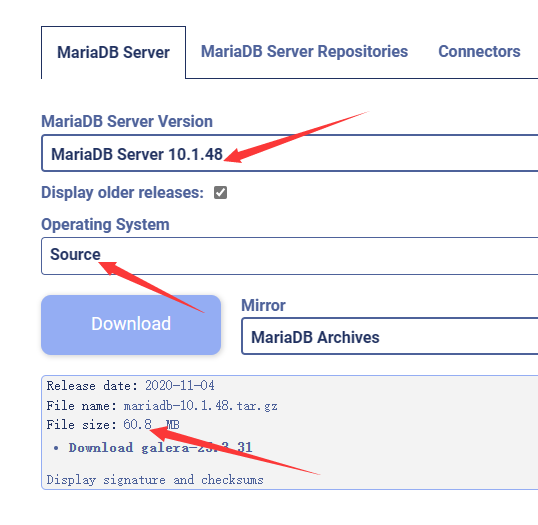
MySQL5.7 与 MariaDB10.1 审计插件兼容性验证
这是一篇关于发现 MariaDB 审计插件导致 MySQL 发生 crash 后,展开适配验证并进行故障处理的文章。 作者:官永强 爱可生DBA 团队成员,擅长 MySQL 运维方面的技能。热爱学习新知识,亦是个爱打游戏的宅男。 本文来源:原创…...

PyTorch Lightning教程五:Debug调试
如果遇到了这样一个问题,当一次训练模型花了好几天,结果突然在验证或测试的时候崩掉了,这个时候其实是很奔溃的,主要还是由于没有提前知道哪些时候会出现什么问题,本节会引入Lightning的Debug方案 1.fast_dev_run参数 …...

末流211无科研保研经验分享
文章目录 个人背景夏令营哈工大威海西工大光电北航软院北邮计算机中科大科学岛 预推免东南软件北航计算机 写在最后心路历程寄语 个人背景 院校:末流211专业背景:计算机科学与技术排名:夏令营7 / 126,预推免3 / 126英语ÿ…...

日期选择器多选换行
<el-form-item label"日期选择"><div class"multi-date-picker"><div class"date-item"><span class"dateIcon"><el-icon><Calendar /></el-icon></span><span class"dateIt…...
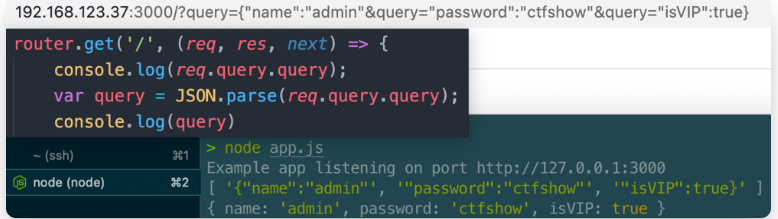
NodeJS原型链污染ctfshow_nodejs
文章目录 NodeJS原型链污染&ctfshow_nodejs前言0x01.原型与原型链0x02.prototype和__proto__分别是什么?0x03.原型链继承不同对象的原型链* 0x04.原型链污染原理0x05.merge()导致原型链污染0x06.ejs模板引擎RCEejs模板引擎另一处rce 0x07.jade模板引擎RCE【ctfs…...

18. SpringBoot 如何在 POM 中引入本地 JAR 包
❤️ 个人主页:水滴技术 🌸 订阅专栏:成功解决 BUG 合集 🚀 支持水滴:点赞👍 收藏⭐ 留言💬 Spring Boot 是一种基于 Spring 框架的轻量级应用程序开发框架,它提供了快速开发应用程…...
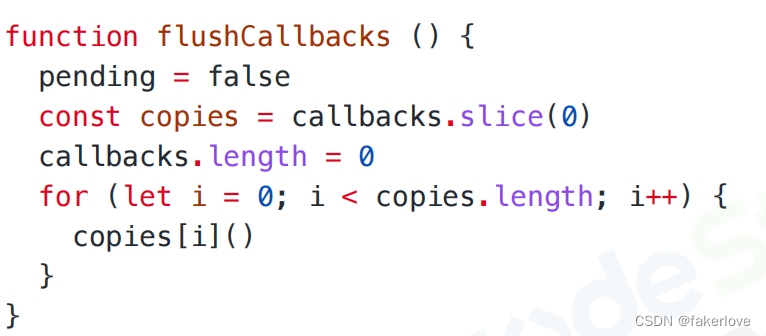
vue2-$nextTick有什么作用?
1、$nextTick是什么? 官方定义:在下次DOM更新循环结束之后执行延迟回调。在修改数据之后立即使用这个方法,获取更新后的DOM。 解释:Vue在更新DOM时是异步执行的,当数据发生变化时,Vue将开启一个异步更新的队…...
python自动收集粘贴板
win10的粘贴板可以用“winV”查看: 每次复制都相当于入栈一个字符串,粘贴相当于获取栈顶。 但是系统自带的这个粘贴板貌似不能一键导出,所以我写了个python代码完成这个功能: import pyperclip import timetmp while True:txt…...
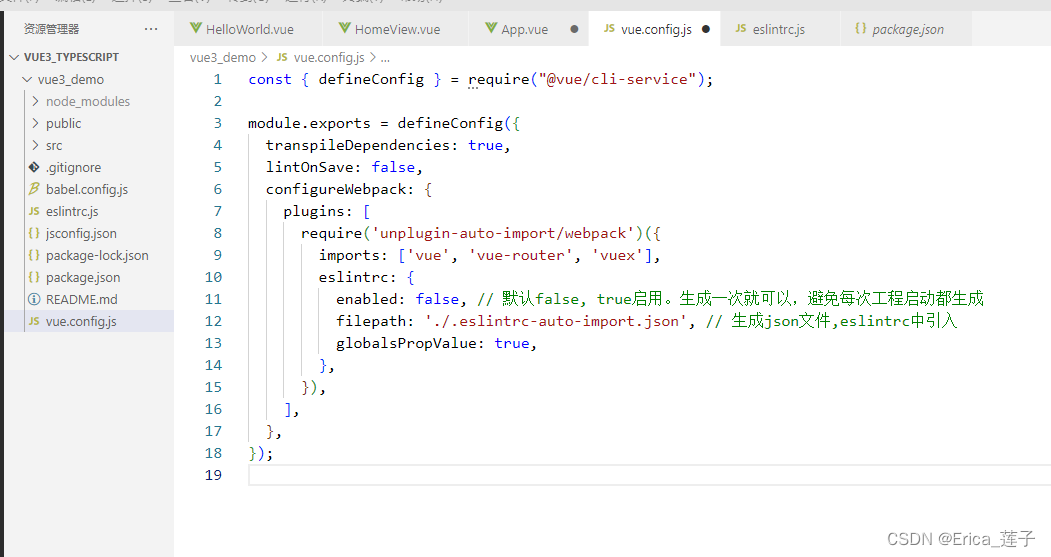
Vue3_语法糖—— <script setup>以及unplugin-auto-import自动引入插件
<script setup>import { ref , onMounted} from vue;let obj ref({a: 1,b: 2,}); let changeObj ()>{console.log(obj)obj.value.c 3 //ref写法}onMounted(()>{console.log(obj)})</script> 里面的代码会被编译成组件 setup() 函数的内容。 相当于 <…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...
