P1993 小 K 的农场
小 K 的农场
题目描述
小 K 在 MC 里面建立很多很多的农场,总共 n n n 个,以至于他自己都忘记了每个农场中种植作物的具体数量了,他只记得一些含糊的信息(共 m m m 个),以下列三种形式描述:
- 农场 a a a 比农场 b b b 至少多种植了 c c c 个单位的作物;
- 农场 a a a 比农场 b b b 至多多种植了 c c c 个单位的作物;
- 农场 a a a 与农场 b b b 种植的作物数一样多。
但是,由于小 K 的记忆有些偏差,所以他想要知道存不存在一种情况,使得农场的种植作物数量与他记忆中的所有信息吻合。
输入格式
第一行包括两个整数 n n n 和 m m m,分别表示农场数目和小 K 记忆中的信息数目。
接下来 m m m 行:
- 如果每行的第一个数是 1 1 1,接下来有三个整数 a , b , c a,b,c a,b,c,表示农场 a a a 比农场 b b b 至少多种植了 c c c 个单位的作物;
- 如果每行的第一个数是 2 2 2,接下来有三个整数 a , b , c a,b,c a,b,c,表示农场 a a a 比农场 b b b 至多多种植了 c c c 个单位的作物;
- 如果每行的第一个数是 3 3 3,接下来有两个整数 a , b a,b a,b,表示农场 a a a 种植的的数量和 b b b 一样多。
输出格式
如果存在某种情况与小 K 的记忆吻合,输出 Yes,否则输出 No。
样例 #1
样例输入 #1
3 3
3 1 2
1 1 3 1
2 2 3 2
样例输出 #1
Yes
提示
对于 100 % 100\% 100% 的数据,保证 1 ≤ n , m , a , b , c ≤ 5 × 1 0 3 1 \le n,m,a,b,c \le 5 \times 10^3 1≤n,m,a,b,c≤5×103。
分析
差分约束模型,把每个都分析一下:
- 农场 a a a 比农场 b b b 至少多种植了 c c c 个单位的作物: x a − c ≥ x b x_a-c \ge x_b xa−c≥xb,构成(a,b,-c)
- 农场 a a a 比农场 b b b 至多多种植了 c c c 个单位的作物: x b + c ≥ x a x_b+c \ge x_a xb+c≥xa,构成(b,a,c)
- 农场 a a a 与农场 b b b 种植的作物数一样多: x a = x b → x a ≥ x b , x b ≥ x a x_a=x_b \to x_a \ge x_b,x_b \ge x_a xa=xb→xa≥xb,xb≥xa,构成(a,b,0),(b,a,0)
代码
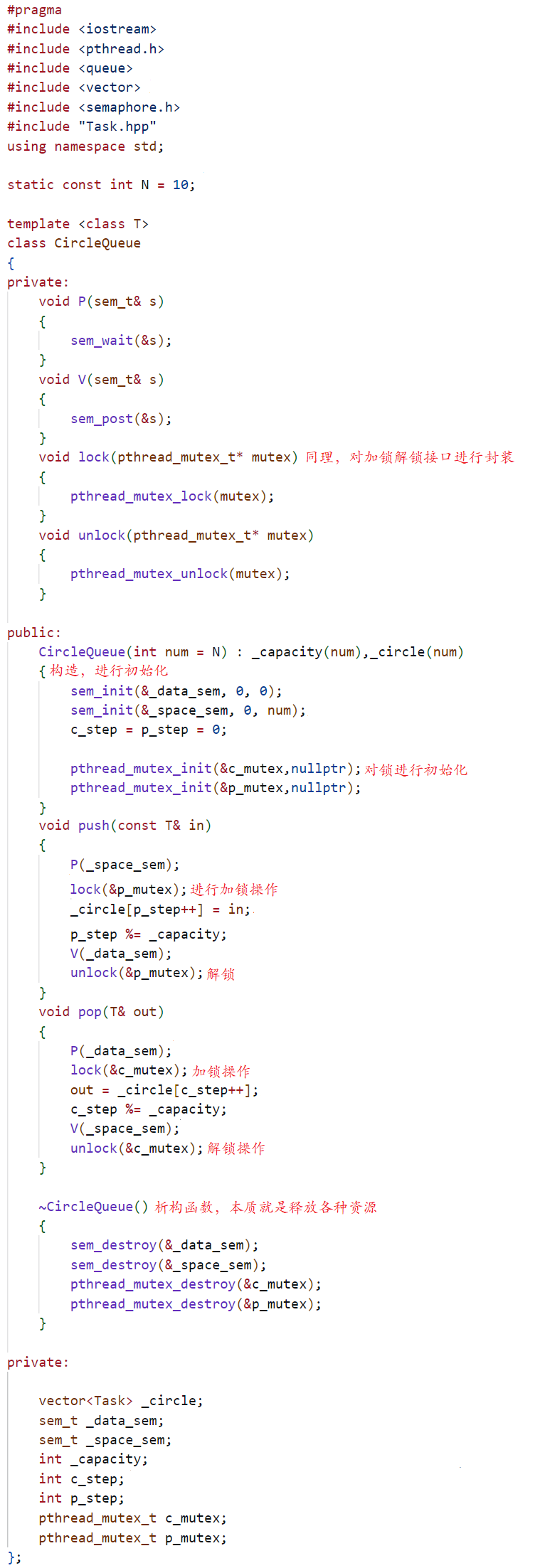
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e8+5,M=1e6;
vector<pair<int,int> > edges[M];
int dis[M];
int n,m,s;
int cnt[M];
bool inQueue[MAXN];
int q[MAXN],f=1,t=1;
void add(int u,int v,int w){edges[u].emplace_back(v,w);}
void read(){cin>>n>>m;for(int i=1,u,v,w,opt;i<=m;i++) {cin>>opt>>u>>v;if(opt<3) cin>>w;if(opt==1) add(u,v,-w);if(opt==2) add(v,u,w);if(opt==3) {add(u,v,0);add(v,u,0);} }
}
bool spfa(int s=0)
{memset(dis,0x3f,sizeof(dis));dis[s]=0;q[t++]=s;inQueue[s]=true;while(f<t){int x=q[f++];inQueue[x]=false;for(auto& edge:edges[x]){if(dis[edge.first]<=dis[x]+edge.second) continue;dis[edge.first]=dis[x]+edge.second;if(!inQueue[edge.first]){q[t++]=edge.first;inQueue[edge.first]=true;cnt[edge.first]++;if(cnt[edge.first]>=n+1) return false;}}}return true;
}
void solve(){for(int i=1;i<=n;i++) add(0,i,0);if(!spfa()) cout<<"No"; else cout<<"Yes";
}
int main()
{read();solve();return 0;
}
分析
1.超级源点
void solve(){for(int i=1;i<=n;i++) add(0,i,0);if(!spfa()) cout<<"No"; else cout<<"Yes";
}
差分约束需要超级源点,需要与每个点构成一条边,权值为0,因为spfa可以有效判断负环,if(cnt[edge.first]>=n+1) return false;需要注意,此处为n+1,因为有超级源点
2.效率问题
STL库中的queue效率低下,常数较高,在不开O2的前提下容易tle,推荐手打队:
- q.push(x) → \to →q[tail++]=x;
- q.pop() → \to → head++;
- q.top() → \to → q[head]
相关文章:

P1993 小 K 的农场
小 K 的农场 题目描述 小 K 在 MC 里面建立很多很多的农场,总共 n n n 个,以至于他自己都忘记了每个农场中种植作物的具体数量了,他只记得一些含糊的信息(共 m m m 个),以下列三种形式描述:…...
Spring boot 集成 Skywalking 配置 || Skywalking 打不开【已解决】
一、Skywalking官网 Apache SkyWalking 1.下载Skywalking APM (如果下载最新的,双击打开闪退,选老点的版本) 2. 下载 Skywalking Agents 如果下载太慢,建议复制下载链接,然后用下载器下载,比…...

手把手教你使用 ftrace 对 Linux 系统进行 debug
1、简介 strace:用来跟踪 Linux 进程执行时的系统调用和接收所接收的信号,可以跟踪到一个进程产生的系统调用,包括参数,返回值,执行消耗的时间。 ftrace:是一个 Linux 内核函数跟踪器,function tracer,旨在帮助开发人员和系统设计者可以找到内核内部发生的事情,从 L…...
【练】要求定义一个全局变量 char buf[] = “1234567“,创建两个线程,不考虑退出条件,打印buf
要求定义一个全局变量 char buf[] "1234567",创建两个线程,不考虑退出条件,另: A线程循环打印buf字符串,B线程循环倒置buf字符串,即buf中本来存储1234567,倒置后buf中存储7654321. 不…...

iOS Viper架构(中文版)【看懂这篇就够了】
完整源码地址 一、iOS_Viper iOS的Viper架构,作为一个从业多年的iOS开发者,我个人认为应该要会一点viper 二、前言 viper的设计模式在iOS开发中不流行,甚至是Swift中,也没有用,我认为比较可惜。作为iOSer,当你掌握…...

深入理解缓存 TLB 原理
今天分享一篇TLB的好文章,希望大家夯实基本功,让我们一起深入理解计算机系统。 TLB 是 translation lookaside buffer 的简称。首先,我们知道 MMU 的作用是把虚拟地址转换成物理地址。 MMU工作原理 虚拟地址和物理地址的映射关系存储在页表…...

获取k8s scale资源对象的命令
kubectl get --raw /apis/<apiGroup>/<apiVersion>/namespaces/<namespaceName>/<resourceKind>/<resourceName>/scale 说明:scale资源对象用来水平扩展k8s资源对象的副本数,它是作为一种k8s资源对象的子资源存在…...

基于ChatYuan-large-v2 语言模型 Fine-tuning 微调训练 广告生成 任务
一、ChatYuan-large-v2 ChatYuan-large-v2是一个开源的支持中英双语的功能型对话语言大模型,与其他 LLM 不同的是模型十分轻量化,并且在轻量化的同时效果相对还不错,仅仅通过0.7B参数量就可以实现10B模型的基础效果,正是其如此的…...
SpringBoot集成Logback日志
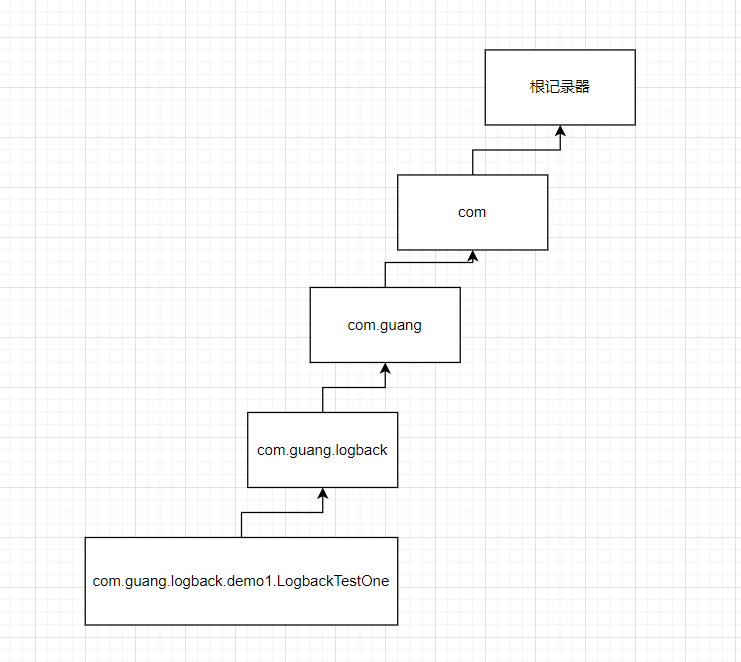
SpringBoot集成Logback日志 文章目录 SpringBoot集成Logback日志一、什么是日志二、Logback简单介绍三、SpringBoot项目中使用Logback四、概念介绍一、日志记录器Logger1.1、日志记录器对象生成1.2、记录器的层级结构1.3、过滤器1.4、logger设置日志级别1.5、java代码演示1.6、…...
MATLAB(R2023a)添加工具箱TooLbox的方法-以GPOPS为例
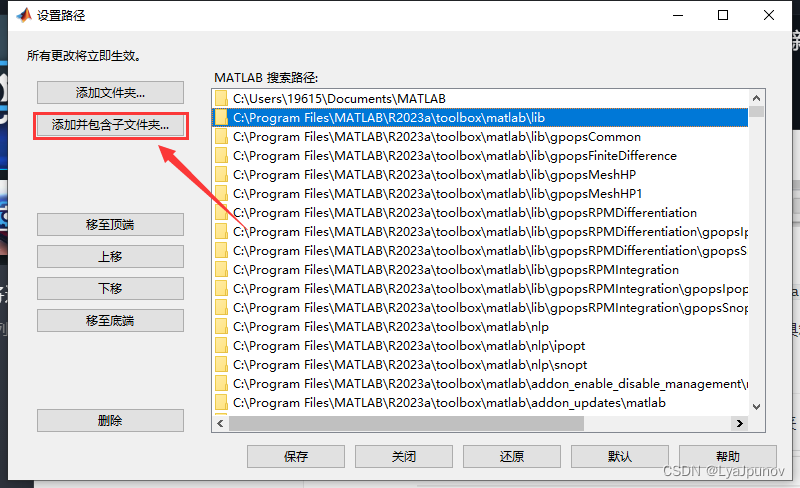
一、找到工具箱存放位置 首先我们需要找到工具箱的存放位置,点击这个设置路径可以看到 我们的matlab工具箱的存放位置 C:\Program Files\MATLAB\R2023a\toolbox\matlab 从资源管理器中打开这个位置,可以看到里面各种工具箱 二、放入工具箱 解压我们…...
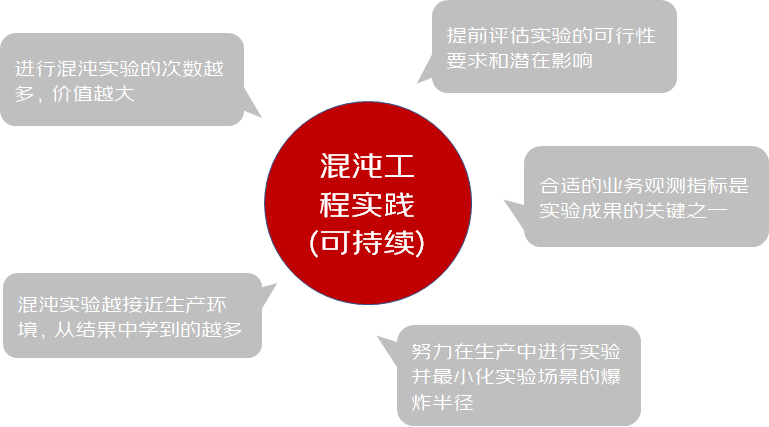
助力618-Y的混沌实践之路 | 京东云技术团队
一、写在前面 1、混沌是什么? 混沌工程(Chaos Engineering)的概念由 Netflix 在 2010 年提出,通过主动向系统中引入异常状态,并根据系统在各种压力下的行为表现确定优化策略,是保障系统稳定性的新型手段。…...

Python系统学习1-4-物理行、逻辑行、选择语句
一、行 (1) 物理行:程序员编写代码的行。 (2) 逻辑行:python解释器需要执行的指令。 (3) 建议: 一个逻辑行在一个物理行上。 如果一个物理行中使用多个逻辑行,需要使用分号;隔开。 (4) 换行: 如果…...
学习系统编程No.35【基于信号量的CP问题】
引言: 北京时间:2023/8/2/12:52,时间飞逝,恍惚间已经来到了八月,给我的第一感觉就是快开学了,别的感觉其实没有,哈哈!看着身边的好友网络相关知识都要全部学完了,就好像…...
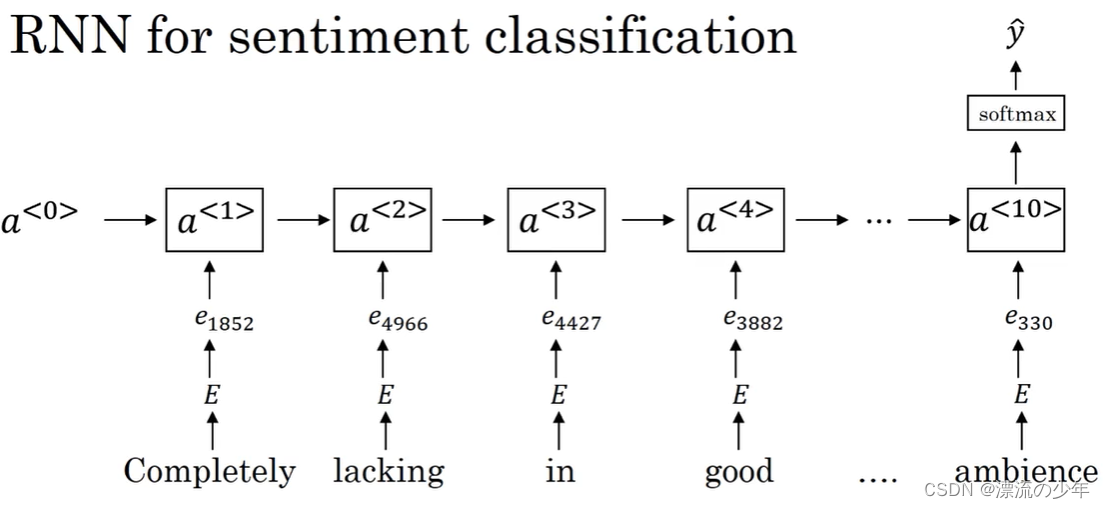
词嵌入、情感分类任务
目录 1.词嵌入(word embedding) 对单词使用one-hot编码的缺点是难以看出词与词之间的关系。 所以需要使用更加特征化的表示(featurized representation),如下图所示,我们可以得到每个词的向量表达。 假设…...

TypeScript使用技巧
文章目录 使用技巧TypeScript内置的工具类型keyofextends 限定泛型interface 与 type 区别 TypeScript作为JavaScript的超集,通过提供静态类型系统和对ES6新特性的支持,使JavaScript开发变得更加高效和可维护。掌握TypeScript的使用技巧,可以帮助我们更好地开发和组织JavaScrip…...
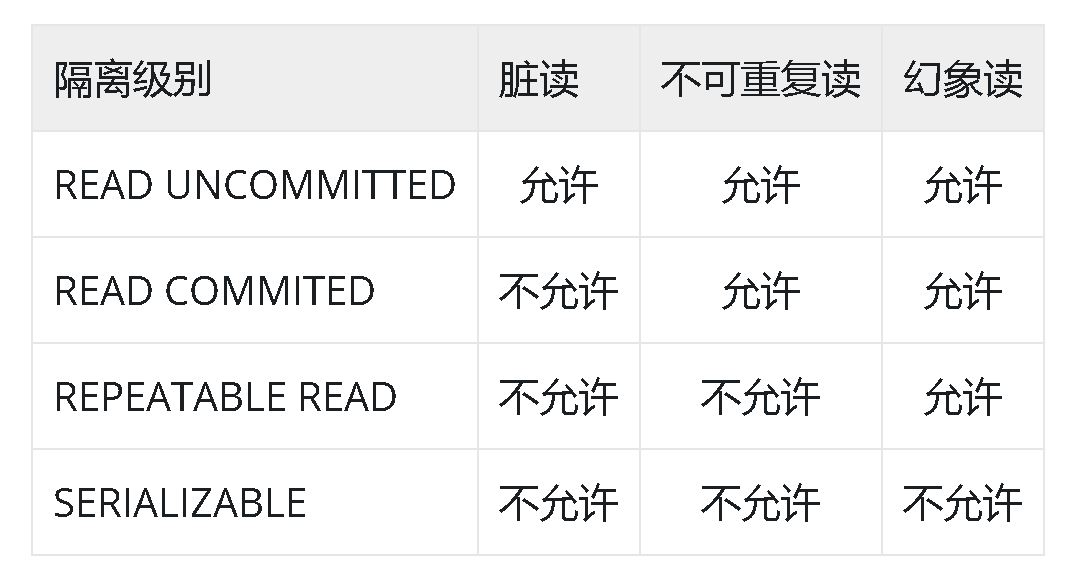
MySQL — InnoDB事务
文章目录 事务定义事务特性事务隔离级别READ UNCOMMITTEDREPEATABLE READREAD COMMITTEDSERIALIZABLE 事务存在的问题脏读(Dirty Read)不可重复读(Non-repeatable Read)幻读(Phantom Read) 事务定义 数据库…...
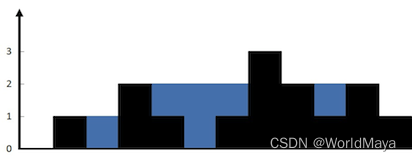
LeetCode 42. 接雨水(动态规划 / 单调栈)
题目: 链接:LeetCode 42. 接雨水 难度:困难 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2…...

顺序表、链表刷题指南(力扣OJ)
目录 前言 题目一:删除有序数组中的重复项 思路: 题解: 题目二:合并两个有序数组 思路: 分析: 题解: 题目三:反转链表 思路: 分析: 题解: 题目四&…...

Lambda表达式总结
Lambda作为Java8的新特性,本篇文章主要想总结一下常用的一下用法和api 1.接口内默认方法实现 public interface Formula {double calculate(int a);// 默认方法default double sqrt(int a) {return Math.sqrt(a);} }public static void main(String[] args) {Form…...

岛屿的最大面积
给你一个大小为 m x n 的二进制矩阵 grid 。 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。 岛屿的面积是岛上值为 1 …...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
