【数据结构与算法】时间复杂度与空间复杂度
目录
一.前言
二.时间复杂度
1.概念
二.大O的渐进表示法
概念:
总结:
三.常见时间复杂度计算举例
例1
例2
例3
例4
例5.计算冒泡排序的时间复杂度
例6.二分算法的时间复杂度
例7.阶乘递归Fac的时间复杂度
例8.斐波那契递归的时间复杂度
四.常见时间复杂度对比
五.空间复杂度
概念
例1
例2
例3
一.前言
从这篇文章开始,C语言的学习就结束了,接下来将会开启数据结构与算法的学习。
早期,计算机刚被发明出来,内存空间并不是很大,所以不仅追求程序运行时的时间效率,还追求空间效率,但发展到今天,已经不太追求空间效率了,时间效率的追求是不变的。
下面就让我们一起学习时间复杂度和空间复杂度是什么吧~
二.时间复杂度
1.概念
1.时间复杂度是一个函数(注意这不是编程语言里的函数,而是数学意义上的函数);
2.这个函数指的是算法跑的次数的函数,并不是算法运行的时间,因为同一个算法在不同的机器上运行的时间可能是不同的,用算法的运行时间表示时间复杂度是欠妥的;
3.一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
二.大O的渐进表示法
概念:
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。需要注意的是算法运行时可能会存在最好情况,最坏情况,平均情况,这个时候我们取最坏情况时的大O;
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
总结:
1.大O里的数就是函数表达式中对结果影响最大的项,或是最大的量级所在的项;
2.如果这个项的系数不是1,那么将它变成1,简单来说,这个项前面的系数得是1;
3.如果函数表达式是个常数,不管这个常数多大,都写成O( 1 );
光说不练假把式,让我们通过例题来更好的理解上述所说吧~
三.常见时间复杂度计算举例
例1
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}不难看出:
Func1 执行的基本操作次数 :
F(N)=N^2+2^N+10
N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010显然最大的量级是 N^2
所以时间复杂度为O(N^2)
例2
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}F(N)=2*N+10
影响最大的项为2*N,因为它的系数不是1,所以要变成1,即
时间复杂度:O(N)
例3
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}F(N)=M+N
由于并未明确告知M和N的关系,所以时间复杂度:O(M+N)
若M远大于N,则为O(M);
若N远大于M,则为O(N);
若亮着差不多大,则为O(N)或O(M);
例4
// 计算Func4的时间复杂度?
void Func4(int)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}F(N)=100
这是一个常数,所以时间复杂度:O(1)
例5.计算冒泡排序的时间复杂度
不了解冒泡算法请戳我
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}最好情况:
原本已排好序,所以进入第二个for循环时不进入if语句,所以exchange==0,直接跳出循环,所以时间复杂度:O(N)
最坏情况:
执行完了所有的循环,所以时间复杂度:O(N^2)
取最坏情况,所以最终的时间复杂度为:O(N^2)
如果没有exchange相关语句,那么最好情况和最坏情况都是O(N^2)
例6.二分算法的时间复杂度
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}最好情况:
第一次就找到了,所以时间复杂度:O(1)
最坏情况:
找到就剩最后一个数才找到
设数组中有N个数,一共找了X次
所以
N/(2*2*2*2.....*2)=1
一共X个2,即:2^X=N -> X=logN(注意这是一个简写,真正的意思是以2为底的N的对数)
所以取最坏情况 ,时间复杂度:O(logN)
例7.阶乘递归Fac的时间复杂度
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}不难看出一共会递归N次,所以时间复杂度为:O(N)
例8.斐波那契递归的时间复杂度
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}对于这种较复杂的时间复杂度的计算可以通过画图来观察;
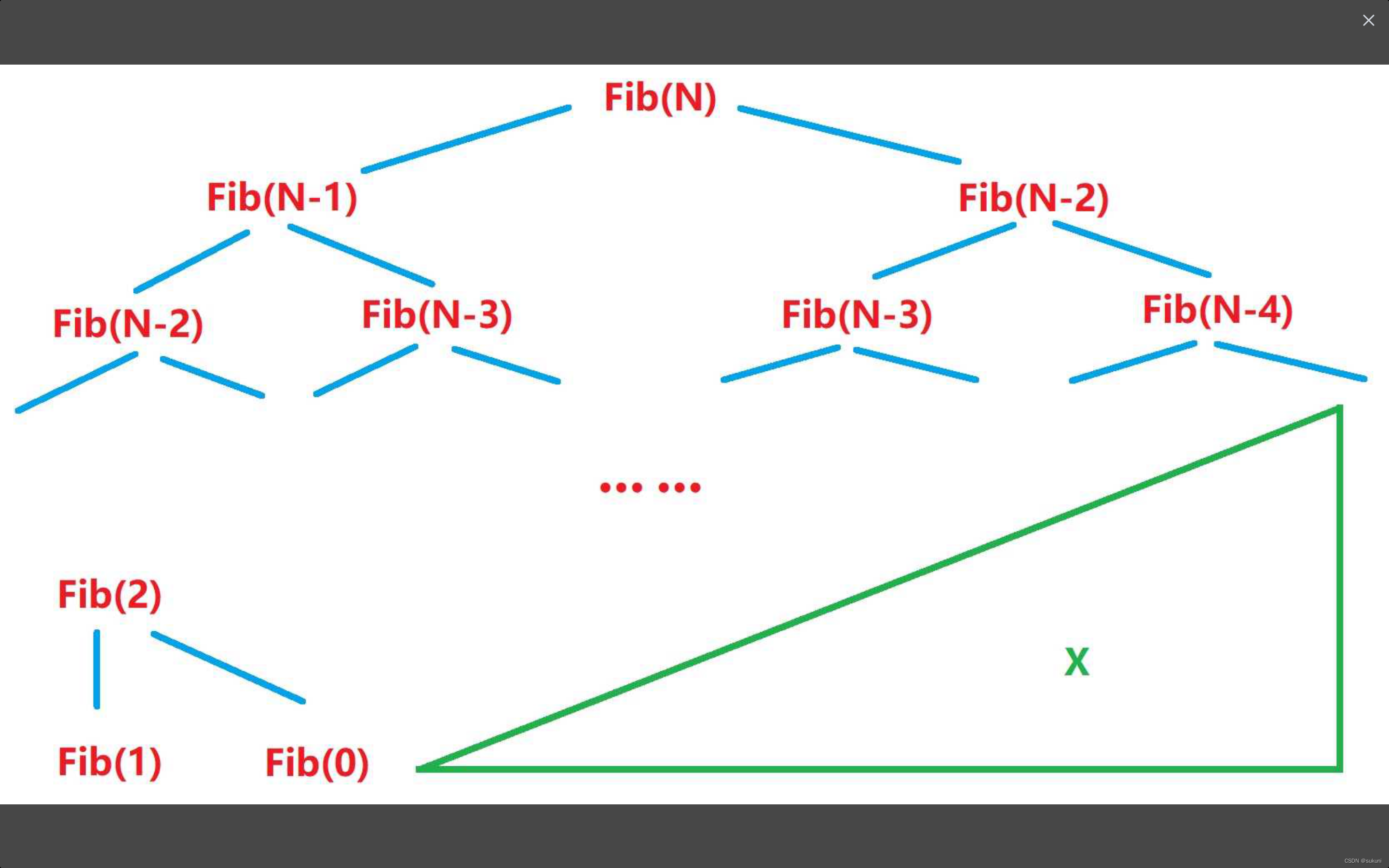

三角形那一块是缺失的部分;
通过上图我们发现,一共会执行F(N)=2^N-X(这个X是一个常数)
所以时间复杂度:O(2^N)
四.常见时间复杂度对比
一般算法常见的复杂度如下:
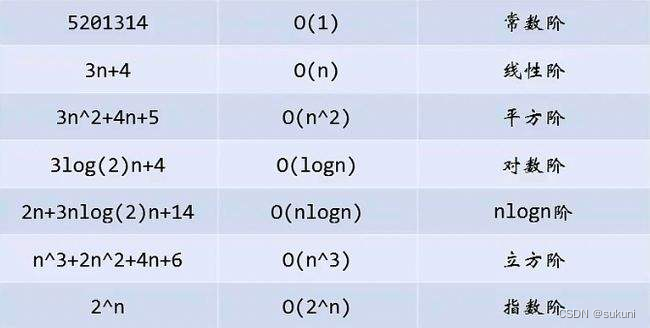
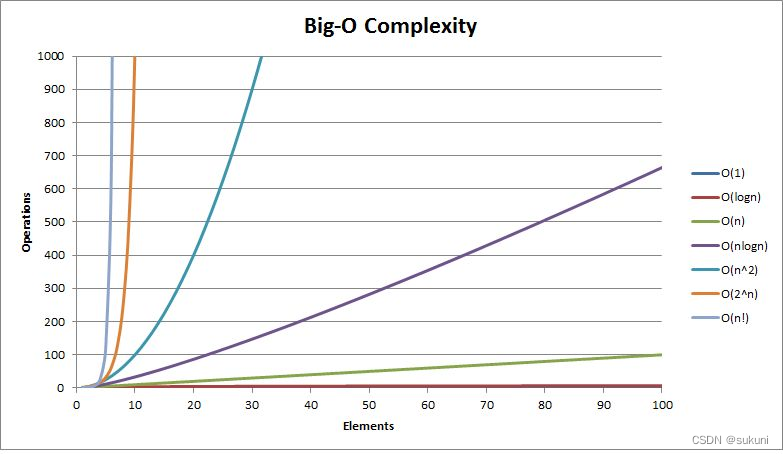
五.空间复杂度
概念
1.空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度;
2.空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数;
3.空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法;
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
例1
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}显然上面的代码带上形参共有5个变量,根据大O渐进法的规则,空间复杂度:O(1);
例2
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}上述代码除了5个变量外,还有malloc函数开辟的n+1个空间,F(N)=n+6,
即空间复杂度:O(n)
例3
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}这是一个递归,每次进入递归时都会再次创建变量,建立栈帧,返回时销毁变量,上述代码啊一共会递归N次,所以会创建N个变量,
即空间复杂度:O(N)
😸😼到此本篇文章就结束了,这是数据结构的第一篇文章,往后也会继续更新的;🤖👻
🥰😍若本篇文章有错误或是有建议,欢迎小伙伴们提出哦;😄🤩
😃😁希望各位大佬们多多支持博主~🤩😍
🦖🐲谢谢你的阅读。🐯🦁
相关文章:

【数据结构与算法】时间复杂度与空间复杂度
目录 一.前言 二.时间复杂度 1.概念 二.大O的渐进表示法 概念: 总结: 三.常见时间复杂度计算举例 例1 例2 例3 例4 例5.计算冒泡排序的时间复杂度 例6.二分算法的时间复杂度 例7.阶乘递归Fac的时间复杂度 例8.斐波那契递归的时间复杂度 …...

Nginx如何配置Http、Https、WS、WSS的方法步骤
这篇文章主要介绍了Nginx如何配置Http、Https、WS、WSS的方法步骤,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧 写在前面 当今互联网领域,Nginx是使…...

【博客621】iptables -J动作总结
iptables -J动作总结 1、iptables常见动作 ACCEPTDROPREJECTLOGSNATDNATMASQUERADEREDIRECT 2、iptables常见动作用法 2-1、ACCEPT: 作用:用于接收匹配的流量,使得流量继续往后面的规则和链路去匹配 2-2、DROP 作用:用于丢弃匹…...
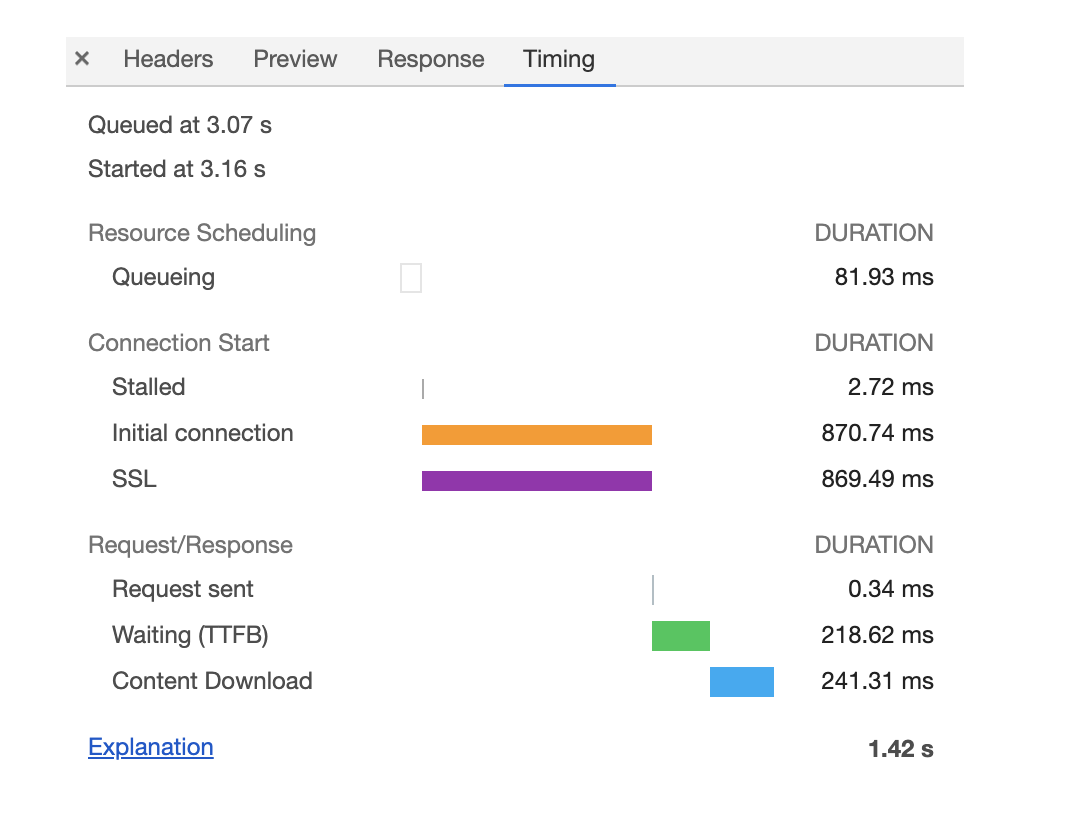
Chrome开发者工具:利用网络面板做性能分析
Chrome 开发者工具(简称 DevTools)是一组网页制作和调试的工具,内嵌于 Google Chrome 浏览器中。 Chrome 开发者工具有很多重要的面板,比如与性能相关的有网络面板、Performance 面板、内存面板等,与调试页面相关的有…...
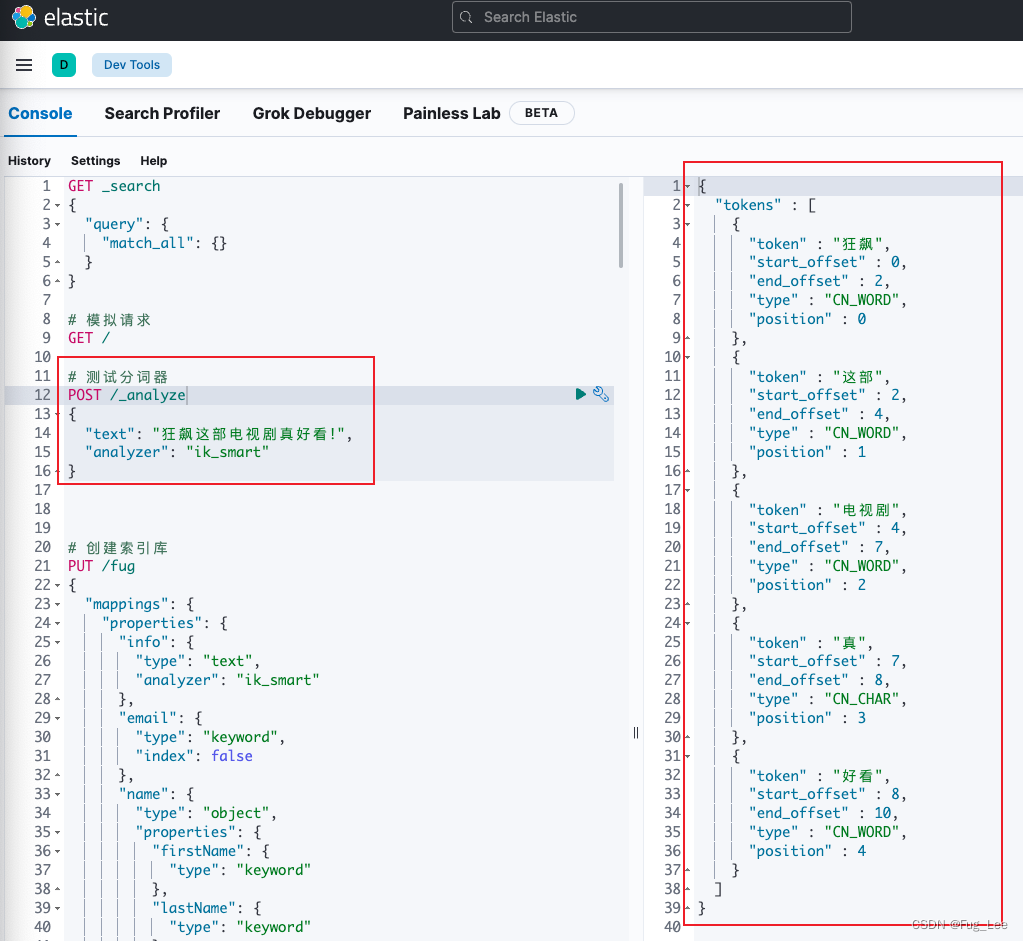
SpringCloud系列(十三)[分布式搜索引擎篇] - ElasticSearch 的概念及 Centos 7 下详细安装步骤
打开淘宝, 搜索 狂飙 会出现各种价格有关狂飙的书籍, 当然也有高启强同款的孙子兵法!!! 如下图所示: 那么面对海量的数据, 如何快速且准确的找到我们想要的内容呢? 淘宝界面已经可以按照综合排序 / 销量 / 信用 / 价格等进行筛选, 是如何做到的呢? ElasticSearch 11 Elastic…...

04_Docker 镜像和仓库
04_Docker 镜像和仓库 文章目录04_Docker 镜像和仓库4.1 什么是 Docker 镜像4.2 列出 Docker 镜像4.3 拉取镜像4.4 查找镜像4.5 构建镜像4.5.1 创建 Docker Hub 账号4.5.2 用 Docker 的 commit 命令创建镜像4.5.3 用 Dockerfile 构建镜像4.5.5 基于 Dockerfile 构建新镜像4.5.5…...
postman-enterprise-API
Postman 是一个用于构建和使用 API 的 API 平台。Postman 简化了 API 生命周期的每个步骤并简化了协作,因此您可以更快地创建更好的 API。 API存储库 在一个中央平台上围绕您的所有 API 工件轻松存储、编目和协作。Postman 可以存储和管理 API 规范、文档、工作流配…...

【ESP 保姆级教程】玩转emqx MQTT篇② ——保留消息和遗嘱消息
忘记过去,超越自己 ❤️ 博客主页 单片机菜鸟哥,一个野生非专业硬件IOT爱好者 ❤️❤️ 本篇创建记录 2023-02-18 ❤️❤️ 本篇更新记录 2023-02-18 ❤️🎉 欢迎关注 🔎点赞 👍收藏 ⭐️留言📝🙏 此博客均由博主单独编写,不存在任何商业团队运营,如发现错误,请…...

开启慢查询日志方法
步骤 开启慢查询日志 SET GLOBAL slow_query_log on;SHOW VARIABLES like slow_query_log;设置时间限制 SET GLOBAL long_query_time 1; -- 单位sSHOW VARIABLES LIKE %long_query_time%;因为long_query_time参数只对新的数据库连接生效,所以还需要重启msql客户端…...
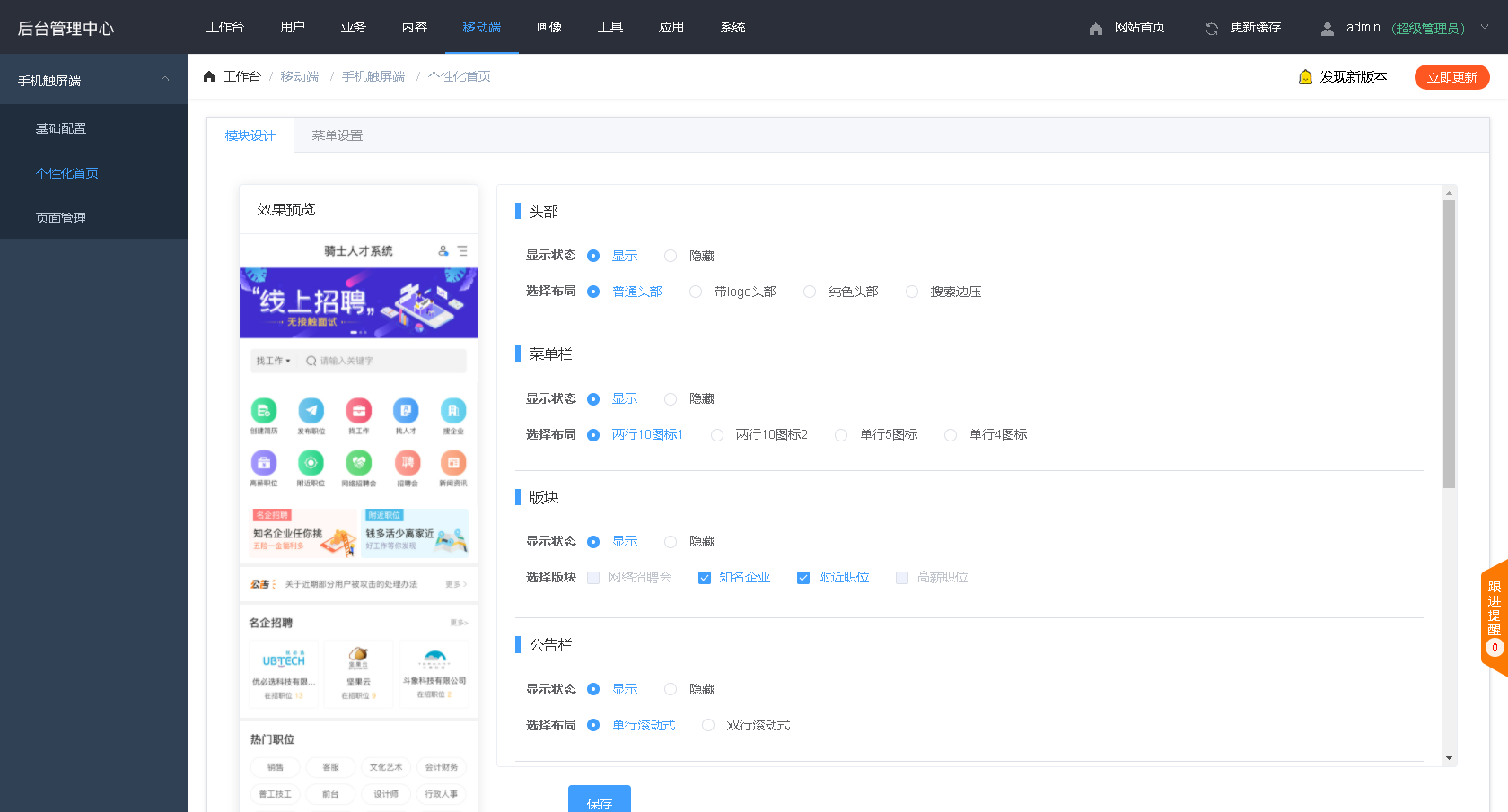
宝塔搭建实战人才求职管理系统admin前端vue源码(二)
大家好啊,我是测评君,欢迎来到web测评。 上一期给大家分享骑士cms后台端在宝塔的搭建部署方式,这套系统是前后端分离的架构,前端是用vue2开发的,还需要在本地打包手动发布上宝塔,所以本期给大家分享&#x…...
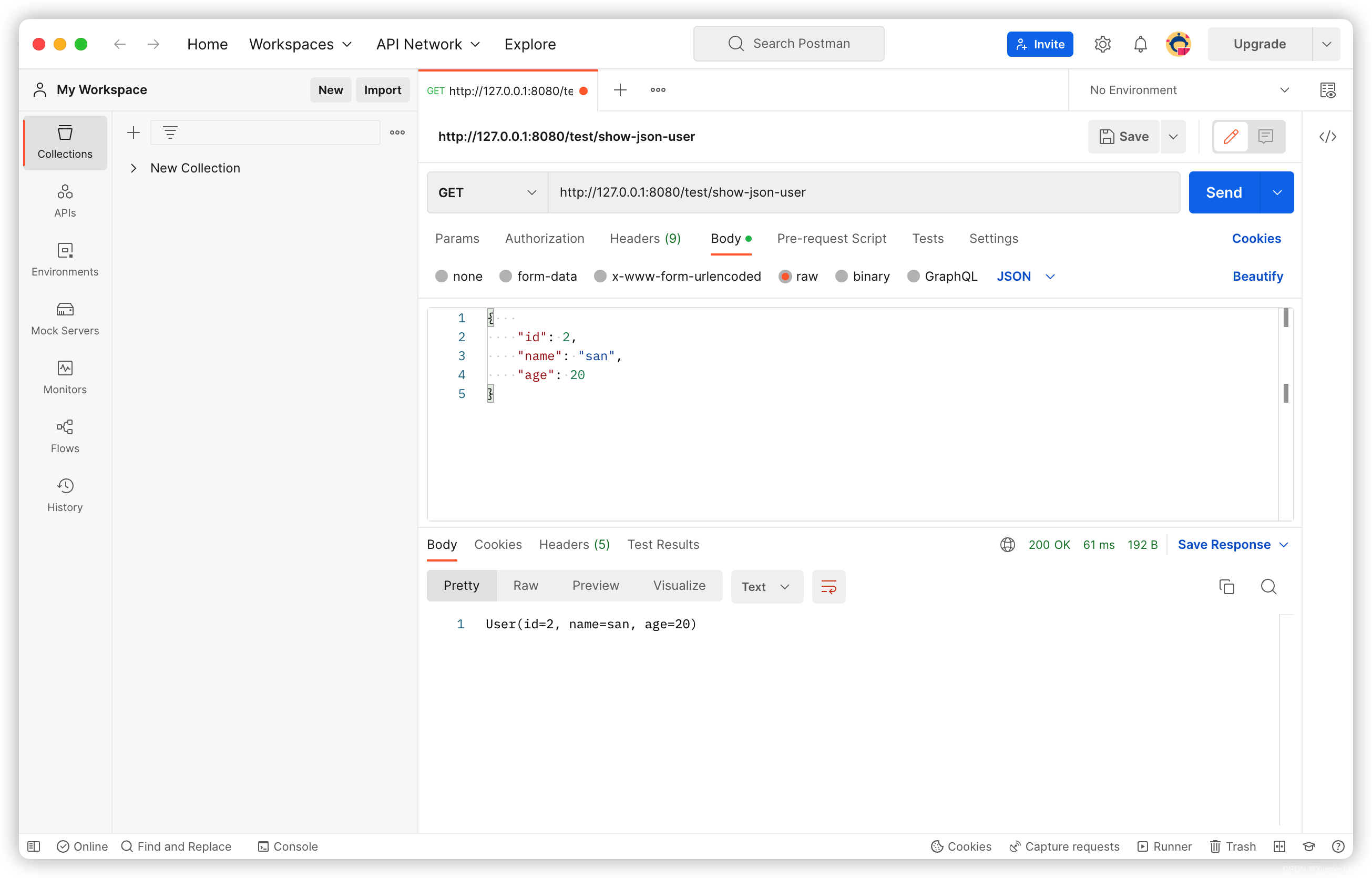
SpringMVC——基础知识
基本概念 SpringMVC是基于servlet api构造的原始web框架,全称是Spring Web MVC 而MVC的全称是Model View Controller,翻译成中文分别是“模型”,“视图”,“控制器”,这是一种软件的架构模式 Model:用来…...

论文浅尝 | SpCQL: 一个自然语言转换Cypher的语义解析数据集
笔记整理:郭爱博,国防科技大学博士论文发表会议:The 31th ACM International Conference on Information and Knowledge Management,CIKM 2022动机随着社交、电子商务、金融等行业的快速发展,现实世界编织出一张庞大而…...

MongoDB 使用规范与限制及最佳实践
MongoDB 灵活文档的优势 灵活库/集合命名及字段增减同一字段可存储不同类型数据Json 文档可多层次嵌套文档对于开发而言最自然的表达 MongoDB 灵活文档的烦恼 数据库集合字段名千奇百怪同一字段数据类型各不一样业务异常可能写入“脏”数据 1.1 库命名规范 不能为空字符串 &…...
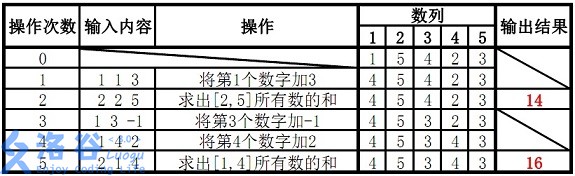
第五十六章 树状数组(一)
第五十六章 树状数组一、前缀和的缺陷二、树状数组1、作用2、算法分析3、算法实现(1)lowbits()(2)插入(3)查询三、例题1、问题题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示2、代码一、前缀和…...
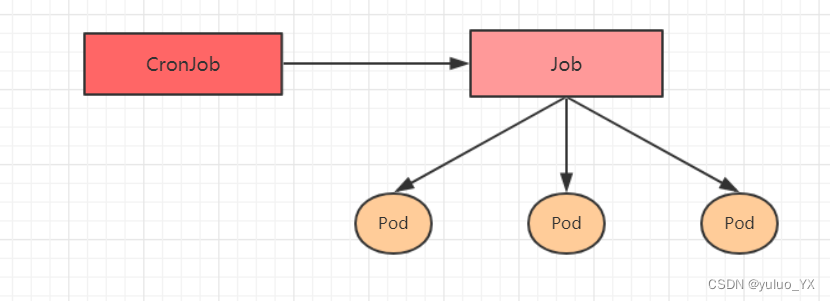
kubernetes教程 --Pod控制器详解
Pod控制器详解 介绍 Pod是kubernetes的最小管理单元,在kubernetes中,按照pod的创建方式可以将其分为两类: 自主式pod:kubernetes直接创建出来的Pod,这种pod删除后就没有了,也不会重建控制器创建的pod&am…...

N2750A Agilent Keysight HP 差分探头1.5GHz
N2750A Agilent Keysight HP 差分探头13554860890 N2750A 是 Agilent Keysight HP 的 1.5 GHz 差分探头。 特征: N2750A:1.5 GHz 衰减比:2:1 或 10:1(可切换) 动态范围: 5 V 或 10 Vpp(10:1 时…...

一文搞懂Linux内核进程CPU调度基本原理
为什么需要调度 进程调度的概念比较简单,我们假设在一个单核处理器的系统中,同一时刻只有一个进程可以拥有处理器资源,那么其他的进程只能在就绪队列中等待,等到处理器空闲之后才有计划获得处理器资源来运行。在这种场景下&#…...
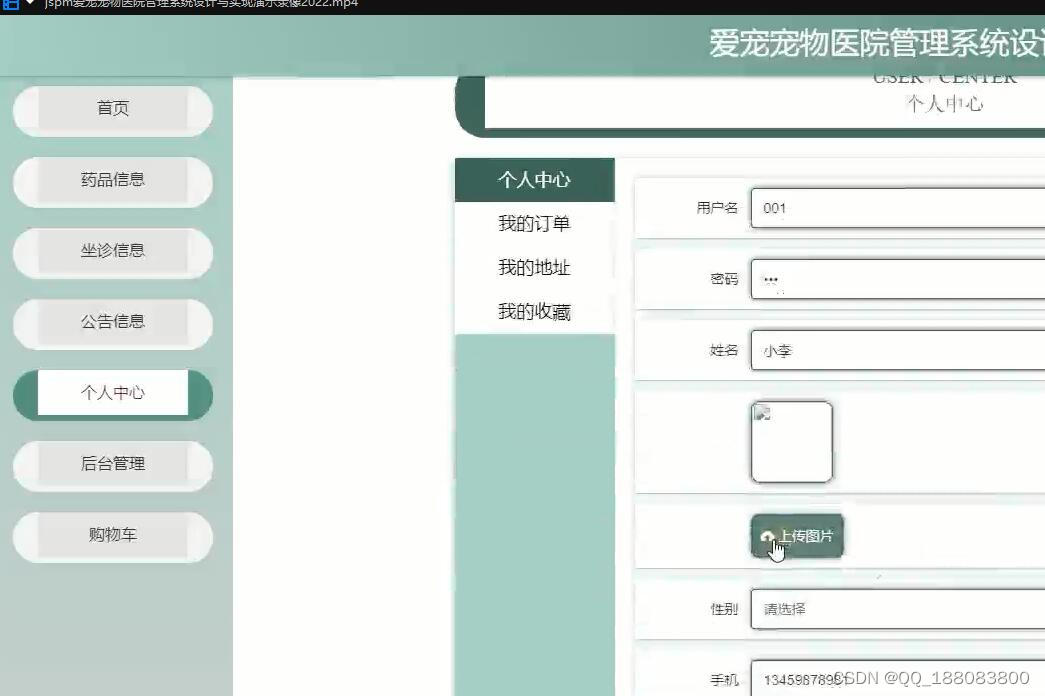
java ssm爱宠宠物医院挂号预约系统管理系统设计与实现
本课题所实现的宠物医院网站是基于网页,它可以实现网上预约挂号,评价等基本功能。用户只要手边有一部手机或者一台电脑,可以上网浏览网页,便可以使用本系统,没有时间和地点的限制,使得就医预约,…...
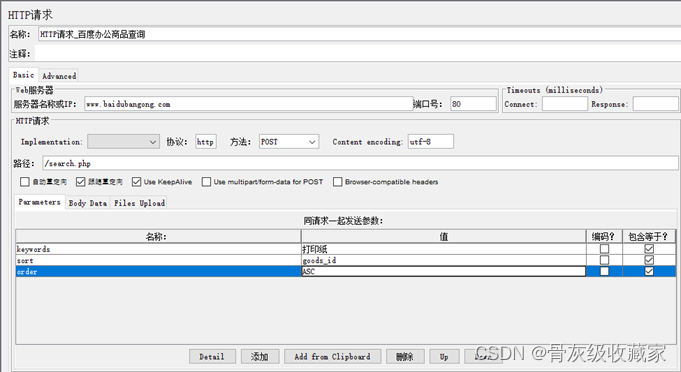
自动化测试工具_Jmeter
【课程简介】 接口测试是测试系统组件间接口的一种测试,接口测试天生为高复杂性的平台带来高效的缺陷监测和质量监督能力,平台越复杂,系统越庞大,接口测试的效果越明显。在接口测试大行其道的今天,测试工具也愈发重要,Jmeter作为一款纯 Java 开发的测试…...

不是所有人都适合职场
一个读者的提问: 洋哥,我目前工作五年在一家大厂,属于那种什么事情上手都很快的人,并且搞定新问题能产生沉浸般的快感。我的本职是程序员,但运营思路产品方法也都会一些,甚至有时候提出的方案效果比产品&a…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
