OSPF 动态路由协议 路由传递
影响OSPF路由选择的因素:
1.OSPF路由的开销值:宽带参考值默认为100. COST=1000/接口带宽。此时接口 带宽的值可更改,更改后只改变参考数值,带宽仍然为初始值。 注意:更改COST需要 在路由的入方向,数据的出方向更改。
2.默认COST与接口类型的关系:
环回口的COST值是1
serial口的COST值是64 T1链路俗称串口 100/1.544=64
标准以太网接口是10 E口 100/10=10
快速以太网是1 F口/E口 100/100=1
千兆以太网接口是1 GE口 100/1000=1
万兆以太网接口是1 Ten GE口 100/10000=1
注意:参考值默认为100. 可修改,修改根据网络中使用的接口类型,以宽带最大为标准进行修改,修改时所运行OSPF的设备均修改。
3.OSPF 路由的AD值:Cisco 110 HUAWEI 内部10 外部150
精确宣告原理:OSPF 宣告一个网段时,OSPF查询本机查询本机所有接口的IP地址,IP地址属于网段内的接口被宣告到OSPF区域中,宣告产生的路由掩码以接口地址掩码为准;精确宣告时代表OSPF进程查询 的地址必须 唯一匹配,只有匹配的接口IP地址才能 宣告,宣告的路由掩码以接口掩码为准。
一个网段宣告一个区域:一个网段通过Network宣告时只能宣告到一个OSPF区域
OSPF华为重分布:重分布不关心区域:将路由条目重分布到一个OSPF进程时,该进程有多个区域将收到这些重分布的路由。
OSPF配置规则:
ospf [进程号] router-id [route-id]
Area [区域]
network [网络号][反掩码] area [区域号]
例子:ospf 1 router-id 1.1.1.1
network 192.168.1.0 0.0.0.255
OSPF重分布配置规则:import-router [路由协议] subnets //加subnets 将所有 子网重分布
例子 :ospf 1 进入ospf 进程
import-router static
OSPF 修改COST值配置:interface [插槽号/编号/接口号]
ospf cost [Metric]
例子:interface g0/0/0
ospf cost 1
OSPF修改参考带宽值配置:ospf [进程号]
bandwitch-reference [ref-bw]
常用show 命令:
display ospf peer //查看邻居
display ospf interface all //查看运行了 ospf 的接口简要信息
display ospf lsdb //查看ospf数据库
reset ospf process //清除ospf 进程,重新建立邻居
AR3设置 ospf 配置 如下其他路由器 同理
ospf 1
area 0.0.0.0
network 3.3.3.0 0.0.0.255
network 13.1.1.0 0.0.0.255
network 34.1.1.0 0.0.0.255 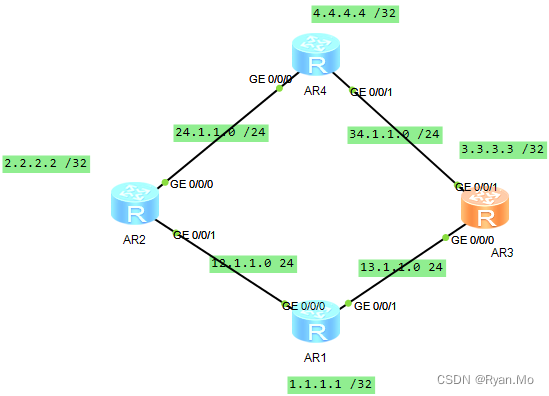
相关文章:

OSPF 动态路由协议 路由传递
影响OSPF路由选择的因素: 1.OSPF路由的开销值:宽带参考值默认为100. COST1000/接口带宽。此时接口 带宽的值可更改,更改后只改变参考数值,带宽仍然为初始值。 注意:更改COST需要 在路由的入方向,数据的出方…...

5.kubeadm安装
文章目录 kubeadm部署环境初始化所有的节点安装Docker所有节点安装kubeadm,kubelet和kubectl初始化方法一,配置文件初始化方法二,命令初始化 网络插件node节点总结 证书过期方法一方法二总结 部署Dashboard kubeadm部署 环境初始化 ###所有…...

【雕爷学编程】Arduino动手做(180)---Seeeduino Lotus开发板2
37款传感器与执行器的提法,在网络上广泛流传,其实Arduino能够兼容的传感器模块肯定是不止这37种的。鉴于本人手头积累了一些传感器和执行器模块,依照实践出真知(一定要动手做)的理念,以学习和交流为目的&am…...

6.5 池化层
是什么:池化层跟卷积层类似有个滑动窗口,用来取一个区域内的最大值或者平均值。 作用:卷积神经网络的最后的部分应该要看到整个图像的全局,通过池化(汇聚)操作,逐渐汇聚要取的像素,最终实现学习全局表示的…...
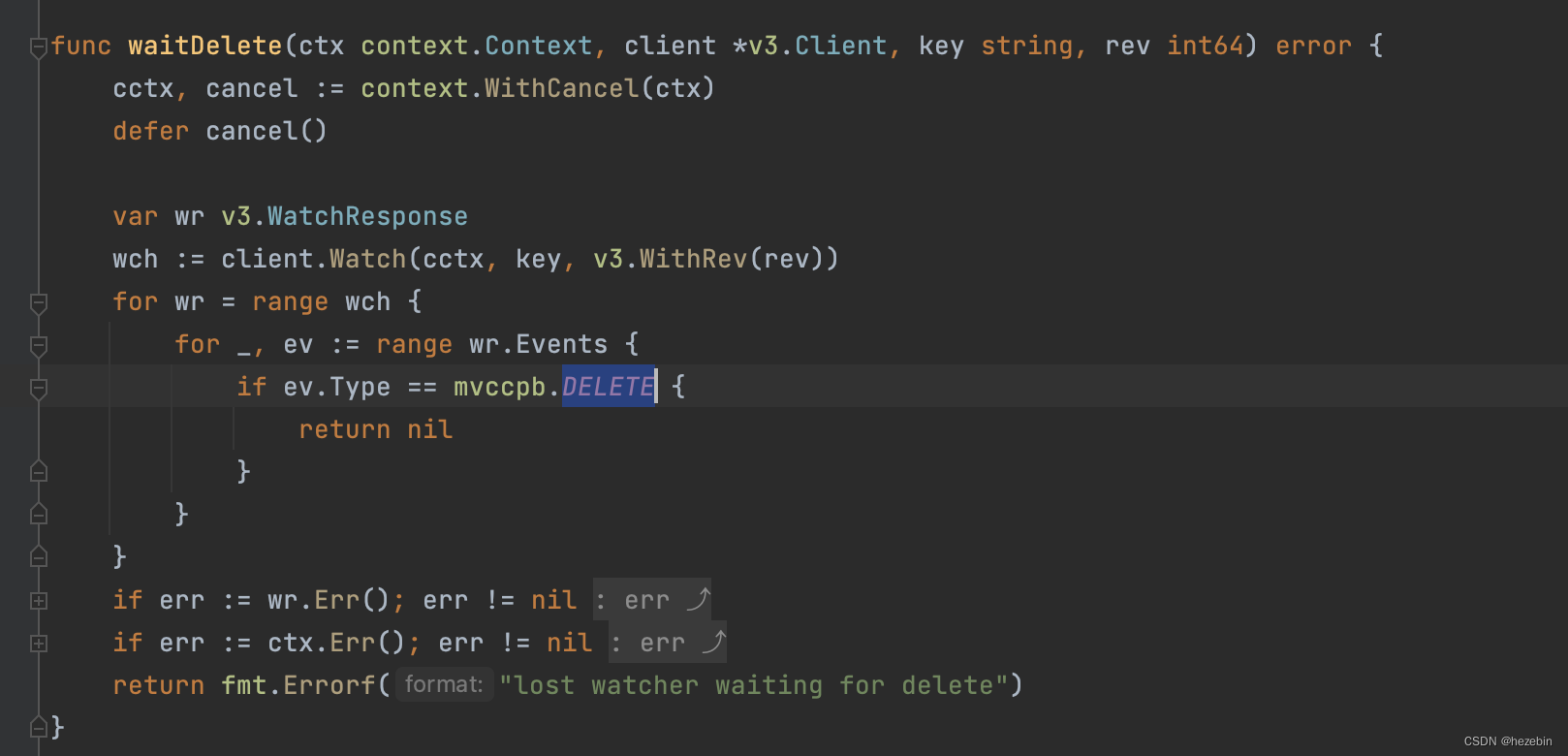
etcd
文章目录 etcd单机安装设置键值对watch操作读取键过往版本的值压缩修订版本lease租约(过期机制)授予租约撤销租约keepAlive续约获取租约信息 事务基于etcd实现分布式锁原生实现官方 concurrency 包实现 服务注册与发现Go 操作 Etcd 参考 etcd etcd 是一…...
W5500-EVB-PICO做DNS Client进行域名解析(四)
前言 在上一章节中我们用W5500-EVB-PICO通过dhcp获取ip地址(网关,子网掩码,dns服务器)等信息,给我们的开发板配置网络信息,成功的接入网络中,那么本章将教大家如何让我们的开发板进行DNS域名解析…...
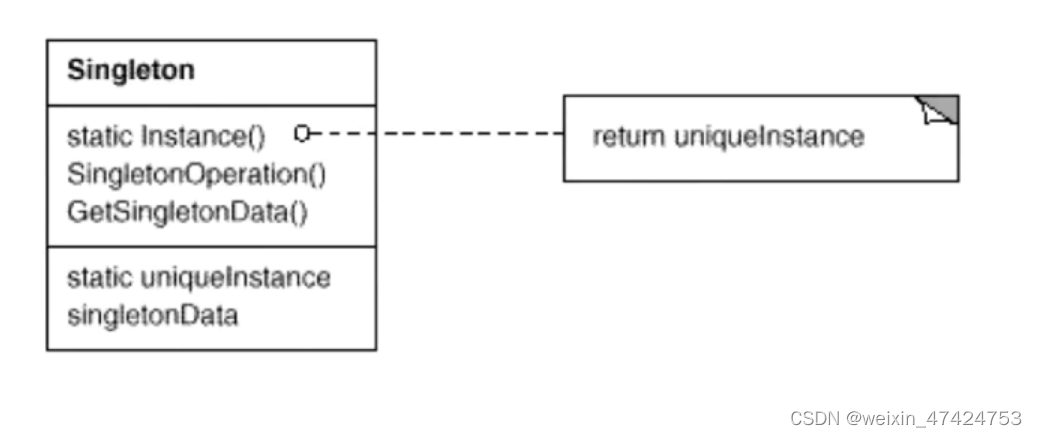
单例模式(C++)
定义 保证一个类仅有一个实例,并提供一个该实例的全局访问点。 应用场景 在软件系统中,经常有这样一些特殊的类,必须保证它们在系统中只存在一个实例,才能确保它们的逻辑正确性、以及良好的效率。如何绕过常规的构造器,提供一种…...
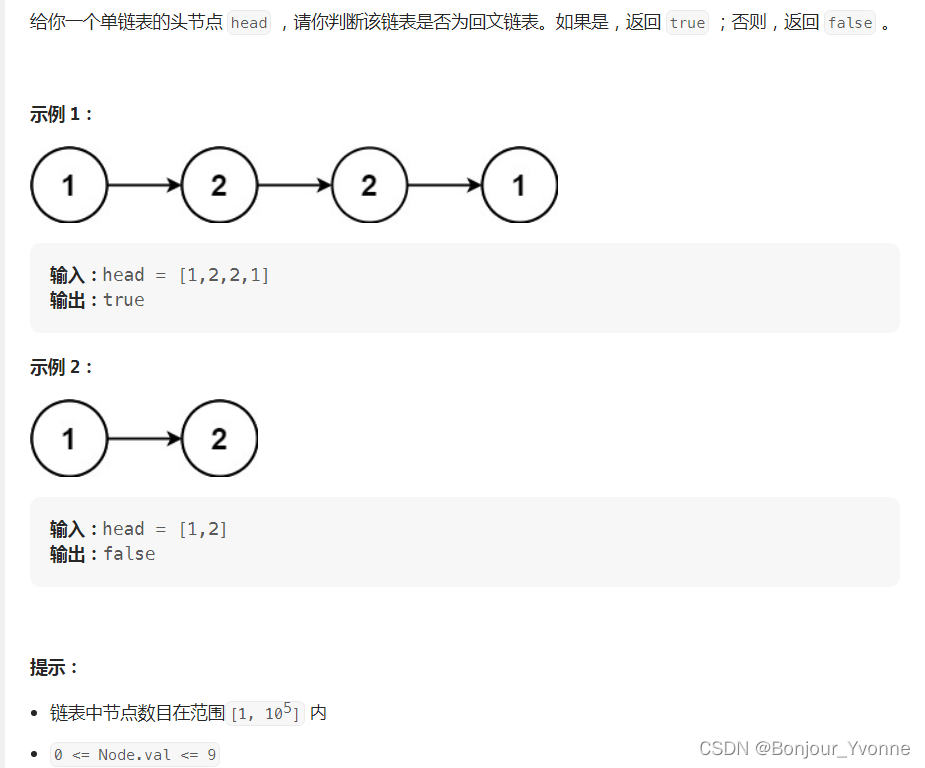
LeetCode 热题 100 JavaScript--234. 回文链表
function ListNode(val, next) {this.val val undefined ? 0 : val;this.next next undefined ? null : next; }var isPalindrome function (head) {if (!head || !head.next) {return true; }// 使用快慢指针法找到链表的中间节点let slow head;let fast head;while …...
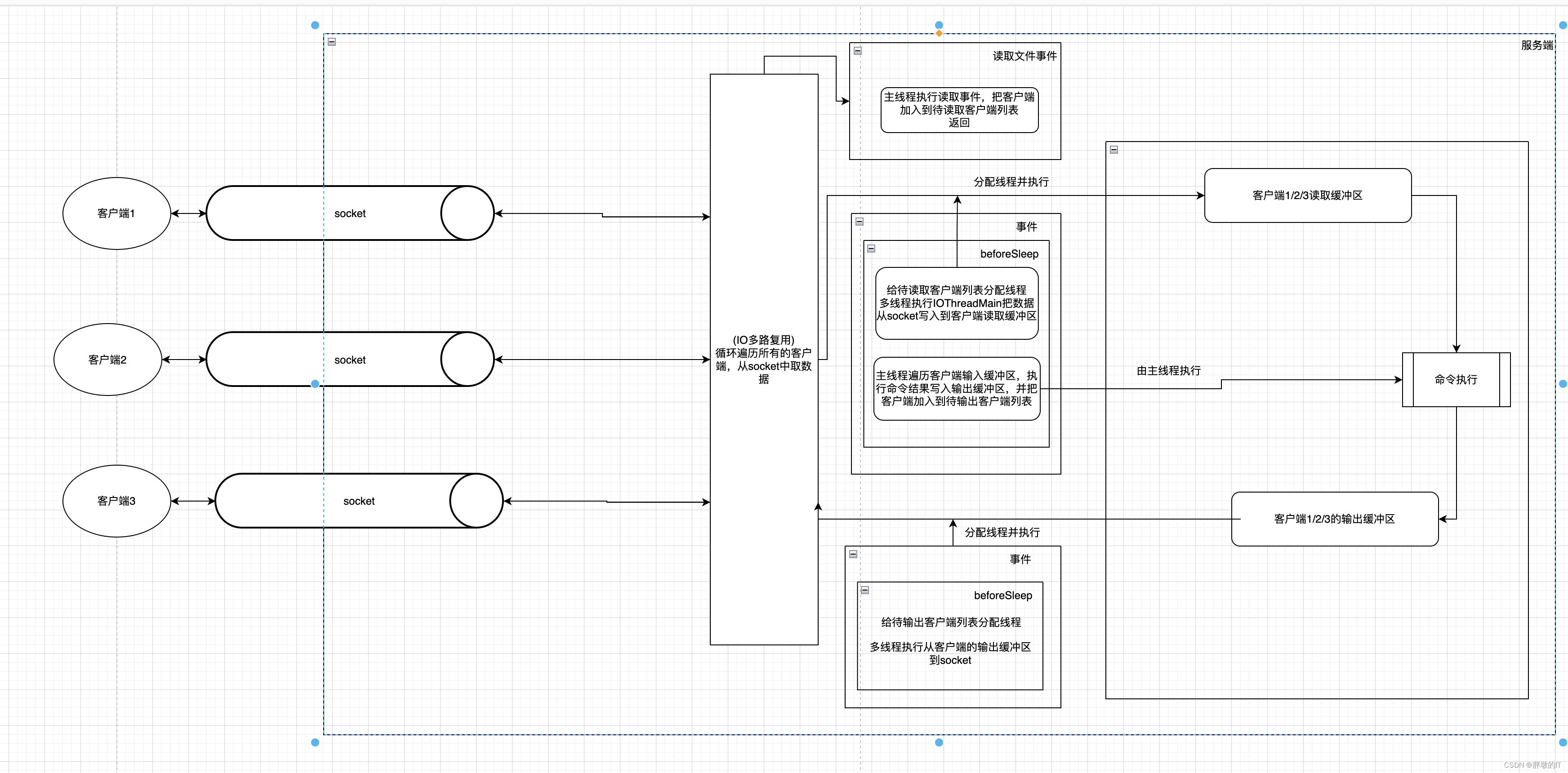
Redis 6.5 服务端开启多线程源码
redis支持开启多线程,只有从socket到读取缓冲区和从输出缓冲区到socket这两段过程是多线程,而命令的执行还是单线程,并且是由主线程执行 借鉴:【Redis】事件驱动框架源码分析(多线程) 一、main启动时初始化…...
)
嵌入式面试笔试刷题(day6)
文章目录 前言一、进程和线程的区别二、共享内存的原理三、中断有传参和返回值吗四、串口数据帧格式五、进程通信有几种,哪几种需要借助内核1.方式2.需要借助内核的 六、flash有哪几种类型七、指针的本质是什么八、指针和数组的区别九、使用宏定义交换变量不能使用中…...
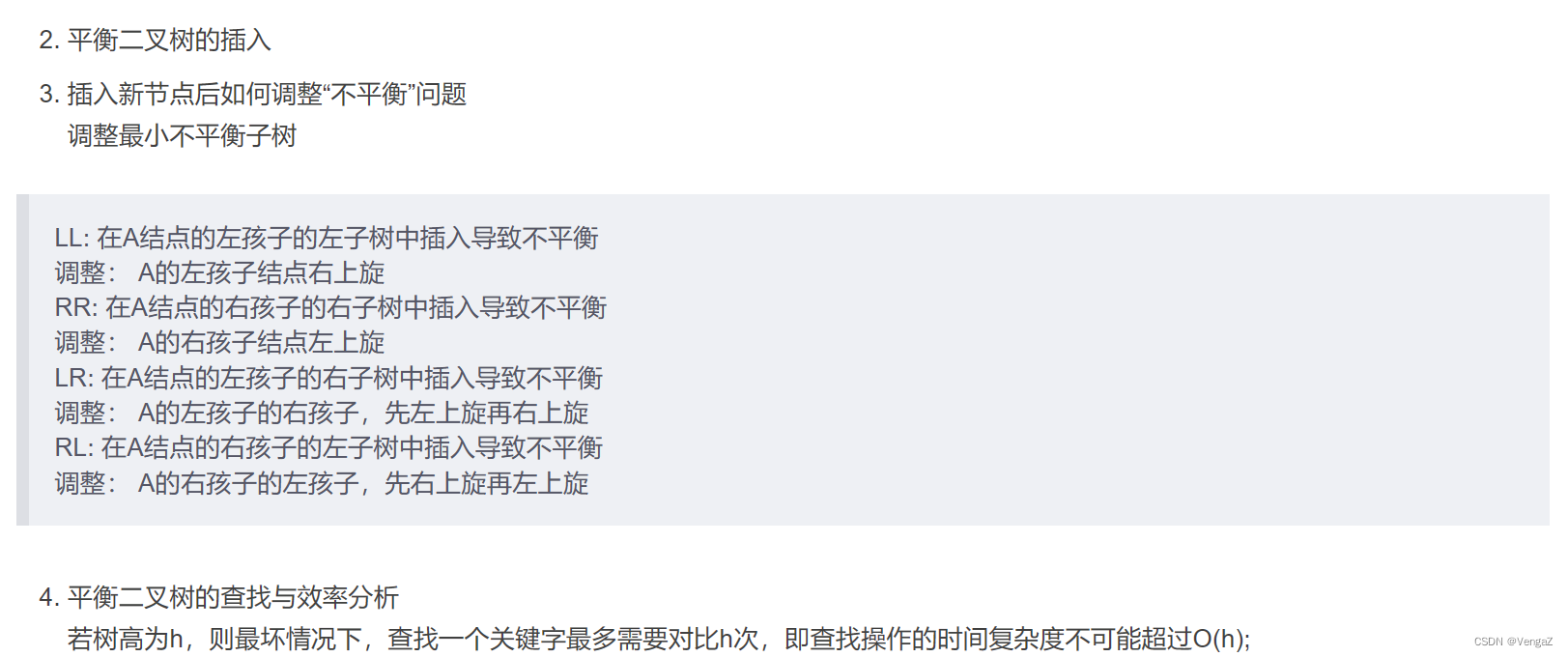
24考研数据结构-第五章:树与二叉树
目录 第五章:树5.1树的基本概念5.1.1树的定义5.1.2 基本术语5.1.3 树的性质 5.2二叉树的概念5.2.1 二叉树的定义与特性5.2.2 几种特殊的二叉树5.2.3 二叉树的性质5.2.4 完全二叉树的性质5.2.5 二叉树的存储结构1. 顺序存储重要的基本操作非完全二叉树2. 链式存储逆向…...

构建稳健的微服务架构:关键的微服务设计原则和最佳实践
在现代软件开发中,微服务架构正逐渐成为构建复杂应用程序的首选方法之一。微服务架构的核心理念是将应用程序划分为一系列小型、自治的服务,每个服务专注于一个特定的业务功能。然而,要实现一个稳健的微服务架构并不仅仅是将功能拆分成微服务…...
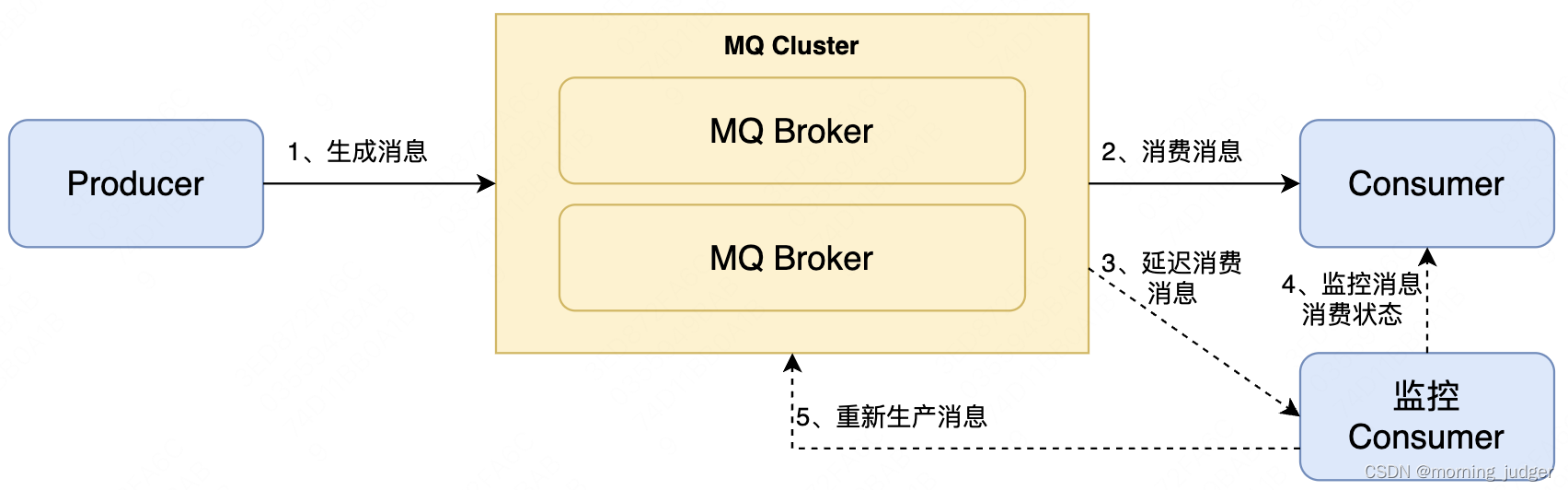
消息队列常见问题(1)-如何保障不丢消息
目录 1. 为什么消息队列会丢消息? 2. 怎么保障消息可靠传递? 2.1 生产者不丢消息 2.2 服务端不丢消息 2.3 消费者不丢消息 3. 消息丢失如何快速止损? 3.1 完善监控 3.2 完善止损工具 1. 为什么消息队列会丢消息? 现在主流…...

Circle of Mistery 2023牛客暑期多校训练营5 B
登录—专业IT笔试面试备考平台_牛客网 题目大意:给出一个n个数的数组a,求一个排列,使其形成的其中一个置换环上的数的和>k,并使产生的逆序对数量最少 1<n<1e3;-1e6<k<1e6;-1e6<ai<1e6 tips:关于置换环是什…...

VC9、VC10、VC11等等各对应什么版本的Visual Studio,以及含义
文章目录 1、_MSC_VER 定义编译器的版本2、示例 1、_MSC_VER 定义编译器的版本 MS VC 15.0 _MSC_VER 1910 (Visual Studio 2017) MS VC 14.0 _MSC_VER 1900 (Visual Studio 2015) MS VC 12.0 _MSC_VER 1800 (VisualStudio 2013) MS VC 11.0 _MSC_VER 1700 (VisualStudio…...

两数相加 LeetCode热题100
题目 给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。 请你将两个数相加,并以相同形式返回一个表示和的链表。 你可以假设除了数字 0 之外,这两个数都不会…...

Python基础 P2数字类型与优先级进阶练习
文章目录 Python基础 P2数字类型与优先级进阶练习1.闰年判断器2.进制转换及求和3.单位转换 Python基础 P2数字类型与优先级进阶练习 1.闰年判断器 简介 对于闰年的判断就是判断输入的内容类型是否符合要求,然后通过逻辑判断和运算得出该年份是否为闰年 举个栗子 …...

CAPL通过继电器实现CAN容错性自动化测试
系列文章目录 文章目录 系列文章目录前言一、环境搭建1.硬件环境2.软件环境3.继电器线路连接图:二、容错性测试方法1.CAN_H与CAN_L短路2.CAN_H与GND短路3.CAN_L与GND短路4.CAN_H与电源短路5.CAN_L与电源短路6.CAN_H断路7.CAN_L断路三、CAPL自动化测试1.测试用例目录2.测试报告…...
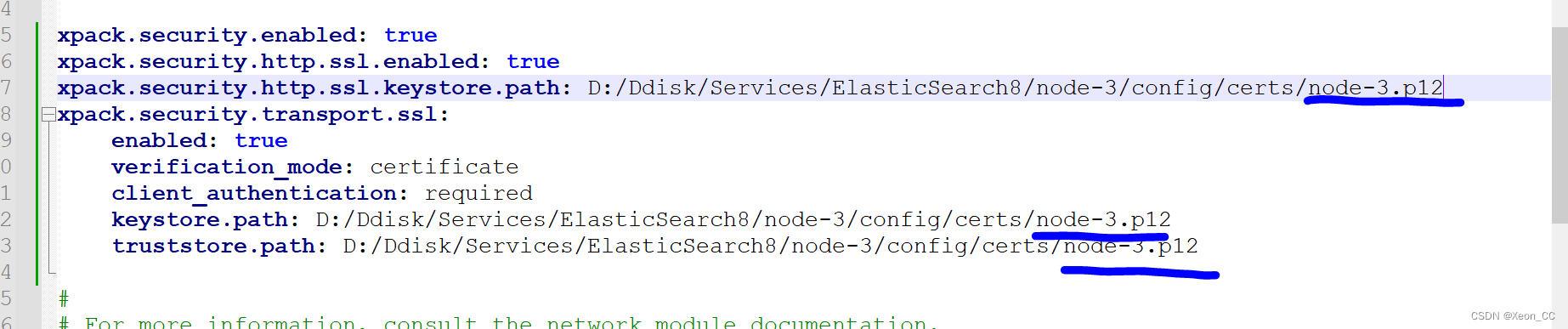
elasticsearch 配置用户名和密码
无密码的其他配置项在:https://blog.csdn.net/Xeon_CC/article/details/132064295 elasticsearch.yml配置文件: xpack.security.enabled: true xpack.security.http.ssl.enabled: true xpack.security.http.ssl.keystore.path: /path/to/elastic-certi…...
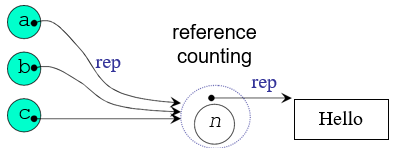
侯捷 C++面向对象编程笔记——9 复合 委托
9 复合 委托 9.1 Composition 复合 类似于c中结构里有结构——class里有class deque 是一个已经存在的功能很多的类(两头进出的队列);利用deque的功能来实现queue的多种操作 该例只是复合的一种情况——设计模式 Adapter 9.1.1 复合下的构造…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
