深度学习:Pytorch常见损失函数Loss简介
深度学习:Pytorch常见损失函数Loss简介
- L1 Loss
- MSE Loss
- SmoothL1 Loss
- CrossEntropy Loss
- Focal Loss
此篇博客主要对深度学习中常用的损失函数进行介绍,并结合Pytorch的函数进行分析,讲解其用法。
L1 Loss
L1 Loss计算预测值和真值的平均绝对误差。
L o s s ( y , y ^ ) = ∣ y − y ^ ∣ Loss(y,\hat{y}) = |y-\hat{y}| Loss(y,y^)=∣y−y^∣
Pytorch函数:
torch.nn.L1Loss(size_average=None, reduce=None, reduction='mean')
参数:
- size_average (bool, optional) – 此参数已弃用;
- reduce (bool, optional) – 此参数已弃用;
- reduction (str, optional) – 由以下三个参数选其一:‘none’ | ‘mean’ | ‘sum’. ‘none’:不对各个元素的误差处理, ‘mean’:输出是各个元素误差的平均值,‘sum’:输出是将各个元素的误差求和。 默认:‘mean’。
MSE Loss
MSE Loss计算预测值和真值的均方误差。
L o s s ( y , y ^ ) = ( y − y ^ ) 2 Loss(y,\hat{y}) = (y-\hat{y})^2 Loss(y,y^)=(y−y^)2
Pytorch函数:
torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')
参数:
- size_average (bool, optional) – 此参数已弃用。
- reduce (bool, optional) – 此参数已弃用。
- reduction (str, optional) – 由以下三个参数选其一:‘none’ | ‘mean’ | ‘sum’. ‘none’:不对各个元素的误差处理, ‘mean’:输出是各个元素误差的平均值,‘sum’:输出是将各个元素的误差求和。 默认:‘mean’。
SmoothL1 Loss
在训练初期,当预测值和真值相差较大时,损失函数的值较大,容易导致训练不稳定,为了防止梯度爆炸(梯度值是指损失函数对输入的导数,梯度爆炸是指梯度值很大),同时当预测值和真值相差较小时,梯度值足够小,可以使用SmoothL1 Loss,它可以视作L1 Loss和L2 Loss(MSE Loss)的结合,计算公式如下:
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ Loss(y,\hat{y}…
Pytorch函数:
torch.nn.SmoothL1Loss(size_average=None, reduce=None, reduction='mean', beta=1.0)
参数:
- size_average (bool, optional) – 此参数已弃用。
- reduce (bool, optional) – 此参数已弃用。
- reduction (str, optional) – 由以下三个参数选其一:‘none’ | ‘mean’ | ‘sum’. ‘none’:不对各个元素的误差处理, ‘mean’:输出是各个元素误差的平均值,‘sum’:输出是将各个元素的误差求和。 默认:‘mean’。
- beta ( float ,optional) – 指定 L1 Loss和 L2 Loss之间变化的阈值。该值必须是非负数。默认值:1.0
CrossEntropy Loss
CrossEntropy Loss是在处理分类问题中常用的一种损失函数,如二分类和多分类。此函数来源于信息论中的交叉熵概念,用于衡量两个预估概率分布和真实概率分布之间的差异。交叉熵损失函数公式如下:
(1)对于二分类问题:
L o s s ( y , y ^ ) = − ∑ i = 1 n ( y i l o g ( y i ^ ) + ( 1 − y i ) l o g ( 1 − y i ^ ) ) Loss(y,\hat{y}) = -\sum_{i=1}^{n}(y_ilog(\hat{y_i})+(1-y_i)log(1-\hat{y_i})) Loss(y,y^)=−i=1∑n(yilog(yi^)+(1−yi)log(1−yi^))
其中, y y y是真值, y ^ \hat{y} y^是预测值,n是样本的数量,每个样本都会计算一个损失,如果reduction是‘mean’,那么会对所有样本的损失求平均;如果reduction是‘sum’,那么会对所有样本的损失求和。
(2)对于多分类问题:
L o s s ( y , y ^ ) = − ∑ i = 1 n ∑ j = 1 m y i j l o g ( y i j ^ ) Loss(y,\hat{y}) = - \sum_{i=1}^{n}\sum_{j=1}^{m}y_{ij}log(\hat{y_{ij}}) Loss(y,y^)=−i=1∑nj=1∑myijlog(yij^)
其中, y i j y_{ij} yij是第i个样本的真实标签在第j类的概率, y i j ^ \hat{y_{ij}} yij^是第i个样本预测为第j类的概率,n是样本数量,m是类别的数量,每个样本都会计算一个损失,如果reduction是‘mean’,那么会对所有样本的损失求平均;如果reduction是‘sum’,那么会对所有样本的损失求和。
Pytorch函数:
torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=- 100, reduce=None, reduction='mean', label_smoothing=0.0)
参数:
- weight (Tensor, optional) – 为每个类指定的手动缩放权重。如果给定,则必须是大小为C的张量。
- size_average (bool, optional) – 此参数已弃用。
- ignore_index (int, optional) – 指定被忽略且不会对输入梯度产生影响的目标值。
- reduce (bool, optional) – 此参数已弃用。
- reduction (str, optional) – 由以下三个参数选其一:‘none’ | ‘mean’ | ‘sum’. ‘none’:不对各个元素的误差处理, ‘mean’:输出是各个元素误差的平均值,‘sum’:输出是将各个元素的误差求和。 默认:‘mean’。
- label_smoothing (float, optional) – [0.0, 1.0] 中的浮点数。指定计算损失时的平滑量,其中 0.0 表示不平滑。默认值: 0.0.
Focal Loss
Focal Loss主要用来处理正负样本(特别是前景和背景样本的分类)不均衡的问题。样本不均衡会导致训练效率低,甚至可能会导致模型退化。Focal Loss可以视为对CrossENtropy Loss增加权重加以平衡(增加预测概率小的样本权重,其对应的损失函数值变大;反而降低预测概率大的样本权重,其对应的损失函数值变小)。参考公式如下:
L o s s ( y , y ^ ) = − ∑ i = 1 n ∑ j = 1 m ( 1 − y i j ^ ) γ y i j l o g ( y i j ^ ) Loss(y,\hat{y}) = - \sum_{i=1}^{n}\sum_{j=1}^{m}(1-\hat{y_{ij}})^{\gamma}y_{ij}log(\hat{y_{ij}}) Loss(y,y^)=−i=1∑nj=1∑m(1−yij^)γyijlog(yij^)
其中, γ \gamma γ常取2.
相关文章:

深度学习:Pytorch常见损失函数Loss简介
深度学习:Pytorch常见损失函数Loss简介 L1 LossMSE LossSmoothL1 LossCrossEntropy LossFocal Loss 此篇博客主要对深度学习中常用的损失函数进行介绍,并结合Pytorch的函数进行分析,讲解其用法。 L1 Loss L1 Loss计算预测值和真值的平均绝对…...

【Android-java】Parcelable 是什么?
Parcelable 是 Android 中的一个接口,用于实现将对象序列化为字节流的功能,以便在不同组件之间传递。与 Java 的 Serializable 接口不同,Parcelable 的性能更高,适用于 Android 平台。 要实现 Parcelable 接口,我们需…...
)
Spring整合MyBatis小实例(转账功能)
实现步骤 一,引入依赖 <!--仓库--><repositories><!--spring里程碑版本的仓库--><repository><id>repository.spring.milestone</id><name>Spring Milestone Repository</name><url>https://repo.spring.i…...

List集合的对象传输的两种方式
说明:在一些特定的情况,我们需要把对象中的List集合属性存入到数据库中,之后把该字段取出来转为List集合的对象使用(如下图) 自定义对象 public class User implements Serializable {/*** ID*/private Integer id;/*…...

海外媒体发稿:软文写作方法方式?一篇好的软文理应合理规划?
不同种类的软文会有不同的方式,下面小编就来来给大家分析一下: 方法一、要选定文章的突破点: 所说突破点就是这篇文章文章软文理应以什么样的视角、什么样的见解、什么样的语言设计理念、如何文章文章的标题来写。不同种类的传播效果&#…...
【秋招】算法岗的八股文之机器学习
目录 机器学习特征工程常见的计算模型总览线性回归模型与逻辑回归模型线性回归模型逻辑回归模型区别 朴素贝叶斯分类器模型 (Naive Bayes)决策树模型随机森林模型支持向量机模型 (Support Vector Machine)K近邻模型神经网络模型卷积神经网络(CNN)循环神经…...
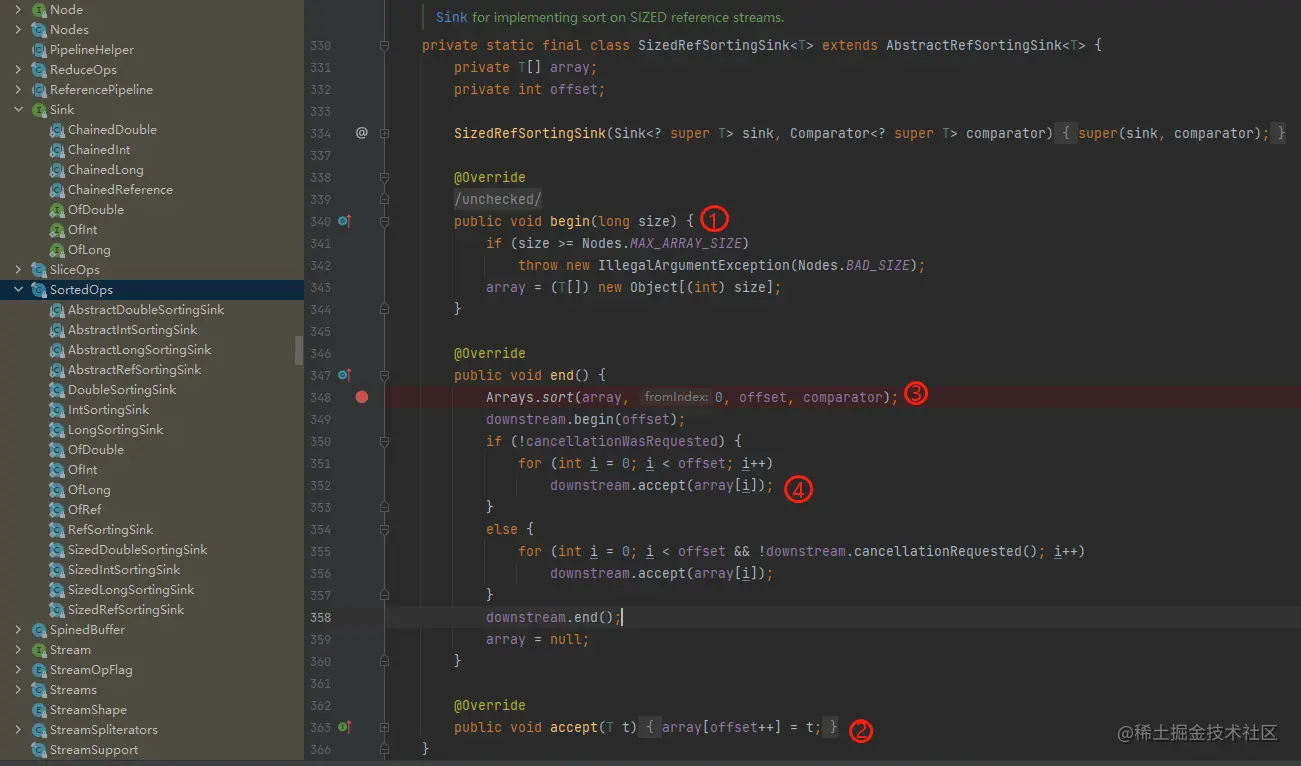
为什么list.sort()比Stream().sorted()更快?
真的更好吗? 先简单写个demo List<Integer> userList new ArrayList<>();Random rand new Random();for (int i 0; i < 10000 ; i) {userList.add(rand.nextInt(1000));}List<Integer> userList2 new ArrayList<>();userList2.add…...

SQL账户SA登录失败,提示错误:18456
错误代码 18456 表示 SQL Server 登录失败。这个错误通常表示提供的凭据(用户名和密码)无法成功验证或者没有权限访问所请求的数据库。以下是一些常见的可能原因和解决方法: 1.错误的凭据:请确认提供的SA账户的用户名和密码是否正…...
Linux 终端操作命令(1)
Linux 命令 终端命令格式 command [-options] [parameter] 说明: command:命令名,相应功能的英文单词或单词的缩写[-options]:选项,可用来对命令进行控制,也可以省略parameter:传给命令的参…...

java与javaw运行jar程序
运行jar程序 一、java.exe启动jar程序 (会显示console黑窗口) 1、一般用法: java -jar myJar.jar2、重命名进程名称启动: echo off copy "%JAVA_HOME%\bin\java.exe" "%JAVA_HOME%\bin\myProcess.exe" myProcess -jar myJar.jar e…...

安装和配置 Home Assistant 教程 HACS Homkit 米家等智能设备接入
安装和配置 Home Assistant 教程 简介 Home Assistant 是一款开源的智能家居自动化平台,可以帮助你集成和控制各种智能设备,从灯光到温度调节器,从摄像头到媒体播放器。本教程将引导你如何在 Docker 环境中安装和配置 Home Assistant&#…...

解决 Android Studio 的 Gradle 面板上只有关于测试的 task 的问题
文章目录 问题描述解决办法 笔者出问题时的运行环境: Android Studio Flamingo | 2022.2.1 Android SDK 33 Gradle 8.0.1 JDK 17 问题描述 笔者最近发现一个奇怪的事情。笔者的 Android Studio 的 Gradle 面板上居然除了用于测试的 task 之外,其它什…...
安全杂记 - 复现nodejs沙箱绕过
目录 一. 配置环境1.下载nodejs2.nodejs配置3.报错解决方法 二. nodej沙箱绕过1. vm模块2.使用this或引用类型来进行沙箱绕过 一. 配置环境 1.下载nodejs 官网:https://nodejs.org/en2.nodejs配置 安装nodejs的msi文件,默认配置一直下一步即可&#x…...

信息安全事件分类分级指南
范围 本指导性技术文件为信息安全事件的分类分级提供指导,用于信息安全事件的防范与处置,为事前准备、事中应对、事后处理 提供一个基础指南,可供信息系统和基础信息传输网络的运营和使用单位以及信息安全主管部门参考使用。 术语和定义 下…...

Vue系列第八篇:echarts绘制柱状图和折线图
本篇将使用echarts框架进行柱状图和折线图绘制。 目录 1.绘制效果 2.安装echarts 3.前端代码 4.后端代码 1.绘制效果 2.安装echarts // 安装echarts版本4 npm i -D echarts4 3.前端代码 src/api/api.js //业务服务调用接口封装import service from ../service.js //npm …...
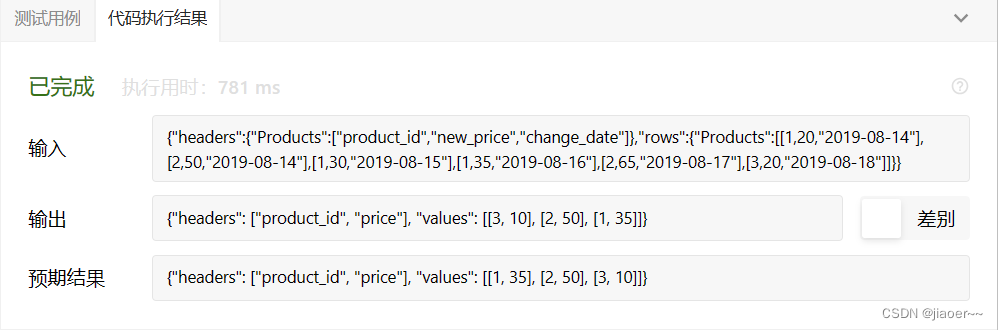
SQL-每日一题【1164. 指定日期的产品价格】
题目 产品数据表: Products 写一段 SQL来查找在 2019-08-16 时全部产品的价格,假设所有产品在修改前的价格都是 10 。 以 任意顺序 返回结果表。 查询结果格式如下例所示。 示例 1: 解题思路 1.题目要求我们查找在 2019-08-16 时全部产品的价格,假设所…...

memcpy、memmove、memcmp、memset函数的作用与区别
一、memcpy与memmove 1、memcpy 作用:从source的位置开始向后复制num个字节的数据到destination的内存位置。 注意: memcpy() 函数在遇到 ’\0’ 的时候不会停下来(strcpy字符串拷贝函数在遇到’\0’的时候会停下来);destination和source…...

socket 到底是个啥
我相信大家在面试过程中或多或少都会被问到这样一个问题:你能解释一下什么是 socket 吗 我记得我当初的回答很是浅显:socket 也叫套接字,用来负责不同主机程序之间的网络通信连接,socket 的表现方式由四元组(ip地址&am…...

奥威BI—数字化转型首选,以数据驱动企业发展
奥威BI系统BI方案可以迅速构建企业级大数据分析平台,可以将大量数据转化为直观、易于理解的图表和图形,推动和促进数字化转型的进程,帮助企业更好地了解自身的运营状况,及时发现问题并采取相应的措施,提高运营效率和质…...

vue中swiper使用
1.引包 说明:导入相应js引css import "Swiper" from "swiper" import "swiper/css/swiper.css"; import "swiper/js/swiper"; 2.结构 说明:必要的结构使用;直接封装成一个组件 <template>…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
