泊松损坏图像的快速尺度间小波去噪研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码及文章
💥1 概述
文献来源:

摘要:
我们提出了一种在泊松噪声存在下图像恢复的快速算法。我们的方法基于(1)最小化泊松噪声MSE的无偏估计,(2)去噪过程的线性参数化,以及(3)在Haar DWT内跨尺度保存泊松统计。MSE估计的最小化在每个小波子带中独立执行,但由于Haar小波的正交性,这相当于全局图像域MSE最小化。这是与标准泊松噪声消除方法的重要区别,特别是那些依赖于数据的非线性预处理来稳定方差的方法。我们的非冗余尺度间小波阈值优于标准方差稳定方案,即使后者应用于平移不变设置(周期旋转)。它还实现了类似于专门为泊松数据开发的最先进的多尺度方法的质量。考虑到我们方法的计算复杂度要低几个数量级,它是一种非常有竞争力的替代方案。所提出的方法在低信号强度和/或大型数据集的背景下特别有前途。这通过生物样品的低计数荧光显微照片的去噪实验来说明。
关键词:
鱼 鳞间 降噪 小波 风险评估 阈值的线性扩展 荧光显微镜
原文摘要:
We present a fast algorithm for image restoration in the presence of Poisson noise. Our approach is based on (1) the minimization of an unbiased estimate of the MSE for Poisson noise, (2) a linear parametrization of the denoising process and (3) the preservation of Poisson statistics across scales within the Haar DWT. The minimization of the MSE estimate is performed independently in each wavelet subband, but this is equivalent to a global image-domain MSE minimization, thanks to the orthogonality of Haar wavelets. This is an important difference with standard Poisson noise-removal methods, in particular those that rely on a non-linear preprocessing of the data to stabilize the variance.Our non-redundant interscale wavelet thresholding outperforms standard variance-stabilizing schemes, even when the latter are applied in a translation-invariant setting (cycle-spinning). It also achieves a quality similar to a state-of-the-art multiscale method that was specially developed for Poisson data. Considering that the computational complexity of our method is orders of magnitude lower, it is a very competitive alternative.The proposed approach is particularly promising in the context of low signal intensities and/or large data sets. This is illustrated experimentally with the denoising of low-count fluorescence micrographs of a biological sample.
关键词:
poisson interscale denoising wavelets risk estimation linear expansion of thresholds fluorescence microscopy
📚2 运行结果

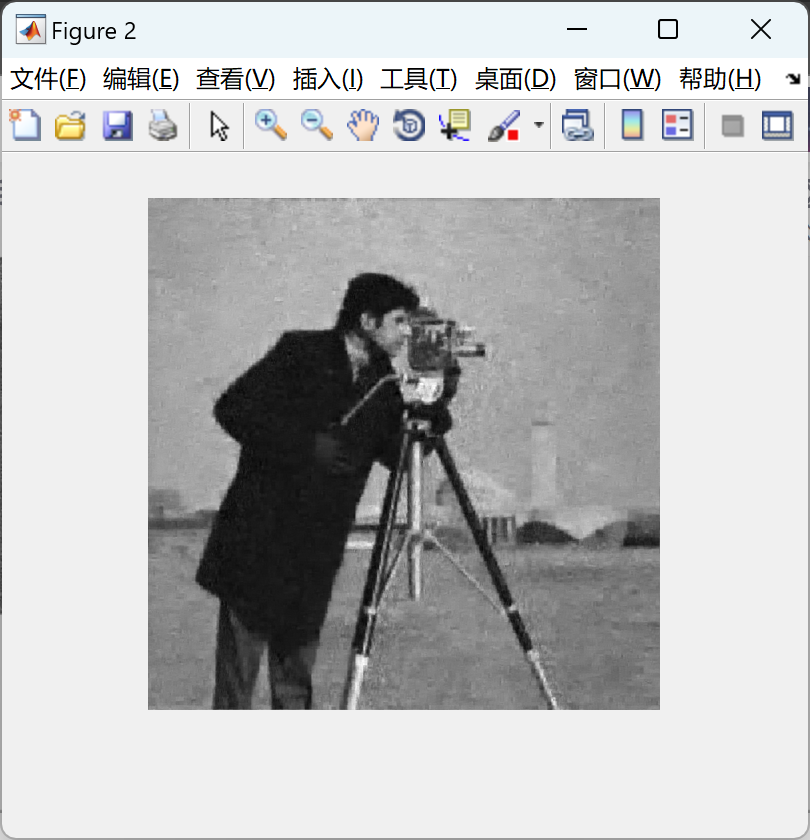
部分代码:
% Y = FAST_CCONV2(X,H,OPT)
% Performs 2D circular convolution. This implementation is fast since it
% uses FFT2 and IFFT2.
%
% Input Parameters:
% X = Input Image.
% H = 2D filter.
% OPT = 'null': No effect, (default option)
% 'nc_shift': treats H as a noncausal filter with origin at
% floor(size(H)/2); the output is shifted by the above
% amount in up-and-left direction to correct the origin.
%
% Output Parameters:
% Y = Circular convolution of X and H. No. of rows of Y is the maximum of
% the number of rows of X and that of H. Simlilarly the no. of columns
% of Y.
function y = fast_cconv2(x,h,opt)
if(~exist('opt','var'))
opt = 'null';
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] F. Luisier, C. Vonesch, T. Blu, M. Unser, "Fast Interscale Wavelet Denoising of Poisson-corrupted Images", Signal Processing, vol. 90, no. 2, pp. 415-427, February 2010.
🌈4 Matlab代码及文章
相关文章:

泊松损坏图像的快速尺度间小波去噪研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

服务器端开发-golang dlv 远程调试
1。需要root权限的服务器代码调试 sudo ./appps to get piddlv attach pid --headless --listen:40000 --api-version2 --accept-multiclientattach the golang IDE or other IDE 2。不需要root权限的服务器代码调试,另一种选择 dlv --listen:40000 --headlesstr…...

STM32F103——时钟配置
目录 1、认识时钟树 1.1 什么是时钟树 1.2 时钟系统解析 1.2.1 时钟源 1.2.2 锁相环PLL 1.2.3 系统时钟SYSCLK 1.2.4 时钟信号输出MCO 2、如何修改主频 2.1 STM32F1时钟系统配置 2.2 STM32F1 时钟使能和配置 下列进行举例的开发板是原子哥的战舰开发板STM32F103ZET…...

【Linux】信号捕捉
目录 信号捕捉1.用户态与内核态1.1关于内核空间与内核态:1.2关于用户态与内核态的表征: 2.信号捕捉过程 信号捕捉 1.用户态与内核态 用户态:执行用户代码时,进程的状态 内核态:执行OS代码时,进程的状态 …...

超详情的开源知识库管理系统- mm-wiki的安装和使用
背景:最近公司需要一款可以记录公司内部文档信息,一些只是累计等,通过之前的经验积累,立马想到了 mm-wiki,然后就给公司搭建了一套,分享一下安装和使用说明: 当前市场上众多的优秀的文档系统百…...

安卓:UDP通信
目录 一、介绍 网络通信的三要素: (1)、IP地址: IPv4: IPv6: IP地址形式: IP常用命令: IP地址操作类: (2)、端口: (3)、协议: UDP协…...

clickhouse安装
clickhouse安装 在线安装和离线安装 一、环境准备: 1.检查系统是否支持clickhouse安装 (向量化支持) grep -q sse4_2 /proc/cpuinfo && echo “SSE 4.2 supported” || echo “SSE 4.2 not supported.” 2.下载对应的clickhouse包 复制运行之后,就会将对应的包加入…...

Cpp学习——string(2)
目录 编辑 容器string中的一些函数 1.capacity() 2.reserve() 3.resize() 4.push_back()与append() 5.find系列函数 容器string中的一些函数 1.capacity() capacity是string当中表示容量大小的函数。但是string开空间时是如何开的呢?现在就来看一下。先写…...

python进阶编程
lambda匿名函数 python使用lambda表达式来创建匿名函数 语法 // lambda 参数们:对参数的处理 lambda x : 2 * x // x 是参数, 2*x 是返回值 //使用lambda实现求和 sum lambda arg1, arg2 : agr1 arg2 print(sum(10,20)) // 将匿名函数封装在一…...

算法练习--leetcode 链表
文章目录 合并两个有序链表删除排序链表中的重复元素 1删除排序链表中的重复元素 2环形链表1环形链表2相交链表反转链表 合并两个有序链表 将两个升序链表合并为一个新的 升序 链表并返回。 新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1: 输入&…...

Android性能优化—Apk瘦身优化
随着业务迭代,apk体积逐渐变大。项目中积累的无用资源,未压缩的图片资源等,都为apk带来了不必要的体积 增加。而APK 的大小会影响应用加载速度、使用的内存量以及消耗的电量。在讨论如何缩减应用的大小之前,有必要了解下应用 APK …...

前端主题切换方案——CSS变量
前言 主题切换是前端开发中老生常谈的问题,本文将介绍主流的前端主题切换实现方案——CSS变量 CSS变量 简介 编写CSS样式时,为了避免代码冗余,降低维护成本,一些CSS预编译工具(Sass/Less/Stylus)等都支…...

Java8 list多属性去重
大家好,我是三叔,很高兴这期又和大家见面了,一个奋斗在互联网的打工人。 在 Java 开发中,我们经常会面临对 List 中的对象属性去重的需求。然而,当需要根据多个属性来进行去重时,情况会稍微复杂一些。本篇…...
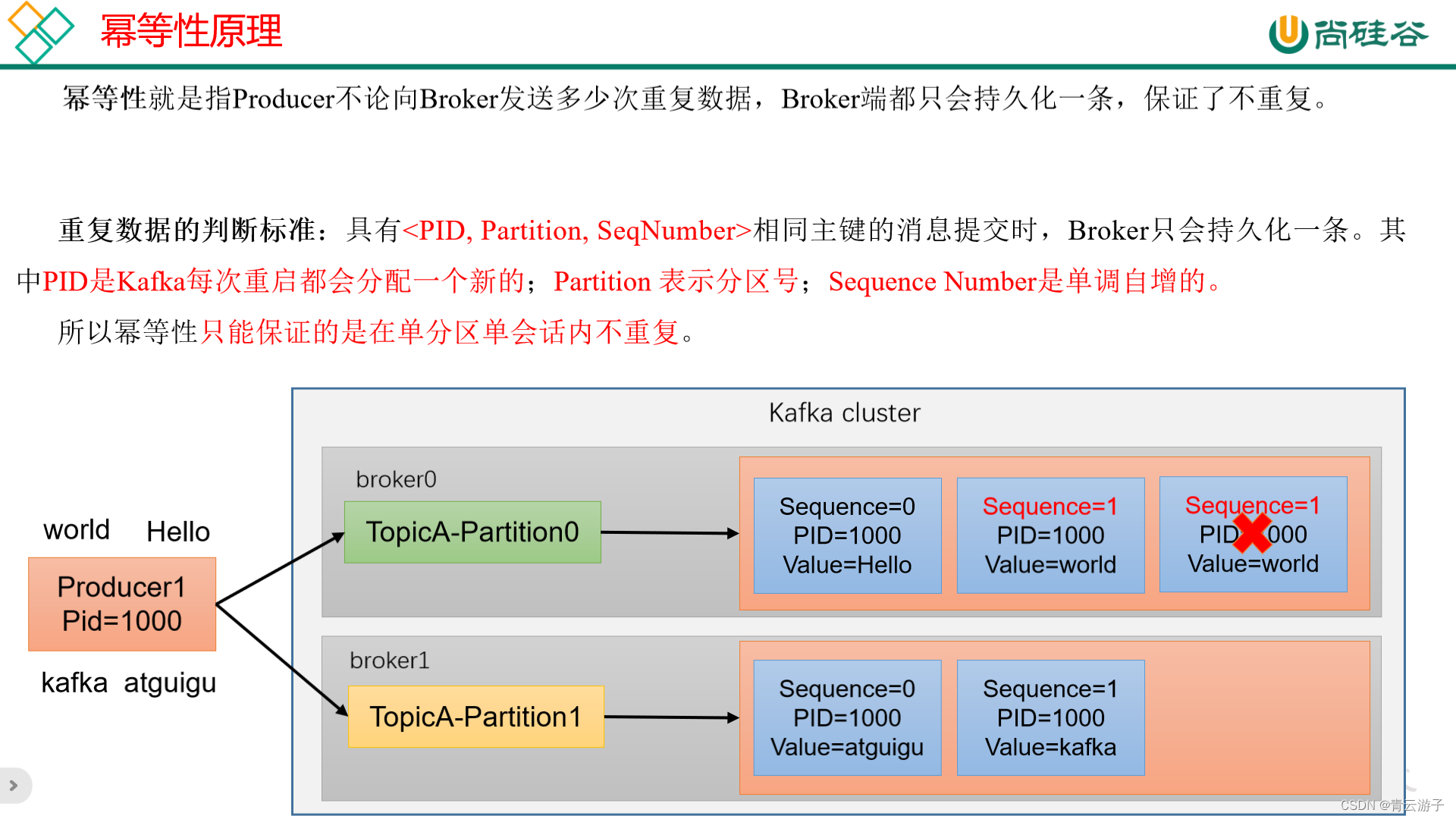
kafka-保证数据不重复-生产者开启幂等性和事务的作用?
1. 生产者开启幂等性为什么能去重? 1.1 场景 适用于消息在写入到服务器日志后,由于网络故障,生产者没有及时收到服务端的ACK消息,生产者误以为消息没有持久化到服务端,导致生产者重复发送该消息,造成了消…...

[AI in security]-214 网络安全威胁情报的建设
文章目录 1.什么是威胁情报2. 威胁情报3. 智能威胁情报3.1 智能威胁情报的组成3.2 整合威胁情报3.3 最佳实践4. 威胁情报的作用5.威胁情报模型6.反杀链模型7.基于TI的局部优势模型参考文献相关的研究1.什么是威胁情报 威胁情报是循证知识,包括环境、机制、指标、意义和可行性…...

Javaweb学习(2)
Javaweb学习 一、Maven1.1 Maven概述1.2 Maven简介1.3、Maven基本使用1.4、IDEA配置Maven1.6、依赖管理&依赖范围 二、MyBatis2.1 MyBatis简介2.2 Mybatis快速入门2.3、解决SQL映射文件的警告提示2.4、Mapper代理开发 三、MyBaits核心配置文件四、 配置文件的增删改查4.1 M…...

leetcode410. 分割数组的最大值 动态规划
hard:https://leetcode.cn/problems/split-array-largest-sum/ 给定一个非负整数数组 nums 和一个整数 m ,你需要将这个数组分成 m 个非空的连续子数组。 设计一个算法使得这 m 个子数组各自和的最大值最小。 示例 1:输入:nums [7,2,5,1…...

C函数指针与类型定义
#include <stdio.h> #define PI 3.14 typedef int uint32_t; /* pfun is a pointer and its type is void (*)(void) */ void (*pfun)(void); /* afer typedef like this we can use “pfun1” as a data type to a function that has form like: / -------…...

最新2024届【海康威视】内推码【GTK3B6】
最新2024届【海康威视】内推码【GTK3B6】 【内推码使用方法】 1.请学弟学妹们登录校招官网,选择岗位投递简历; 2.投递过程中填写内推码完成内推步骤,即可获得内推特权。 内推码:GTK3B6 内推码:GTK3B6 内推码&…...

边写代码边学习之LSTM
1. 什么是LSTM 长短期记忆网络 LSTM(long short-term memory)是 RNN 的一种变体,其核心概念在于细胞状态以及“门”结构。细胞状态相当于信息传输的路径,让信息能在序列连中传递下去。你可以将其看作网络的“记忆”。理论上讲&a…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

