第三章 图论 No.1单源最短路及其综合应用
文章目录
- 1129. 热浪
- 1128. 信使
- 1127. 香甜的黄油
- 1126. 最小花费
- 920. 最优乘车
- 903. 昂贵的聘礼
- 1135. 新年好
- 340. 通信线路
- 342. 道路与航线
- 341. 最优贸易
做乘法的最短路时,若权值>=0,只能用spfa来做,相等于加法中的负权边
1129. 热浪
1129. 热浪 - AcWing题库

单源最短路,稀疏图,用堆优化Dijkstra即可,就是板子套了个背景
// 稀疏图,用堆优化Dijkstra存储
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;const int N = 2510, M = 2 * 6210;
typedef pair<int, int> PII;
priority_queue<PII, vector<PII>, greater<PII>> q;
int h[N], e[M], ne[M], w[M], idx = 1;
int n, m, start, ed;
int dis[N];
bool st[N];void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void dijkstra()
{memset(dis, 0x3f, sizeof(dis));dis[start] = 0;q.push({0, start});while (q.size()){auto t = q.top(); q.pop();int x = t.second, d = t.first;if (st[x]) continue;st[x] = true;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (dis[y] > d + w[i]){dis[y] = d + w[i];q.push({dis[y], y});}}}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d%d%d", &n, &m, &start, &ed);int x, y, d;for (int i = 1; i <= m; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, d), add(y, x, d);}dijkstra();printf("%d\n", dis[ed]);return 0;
}
debug:由于是无向图,边的数量要开两倍。但是w[N]没改,debug了很久
所以e[M], ne[M], w[M],只有h[N],其他的数组存储的都是边
1128. 信使
1128. 信使 - AcWing题库
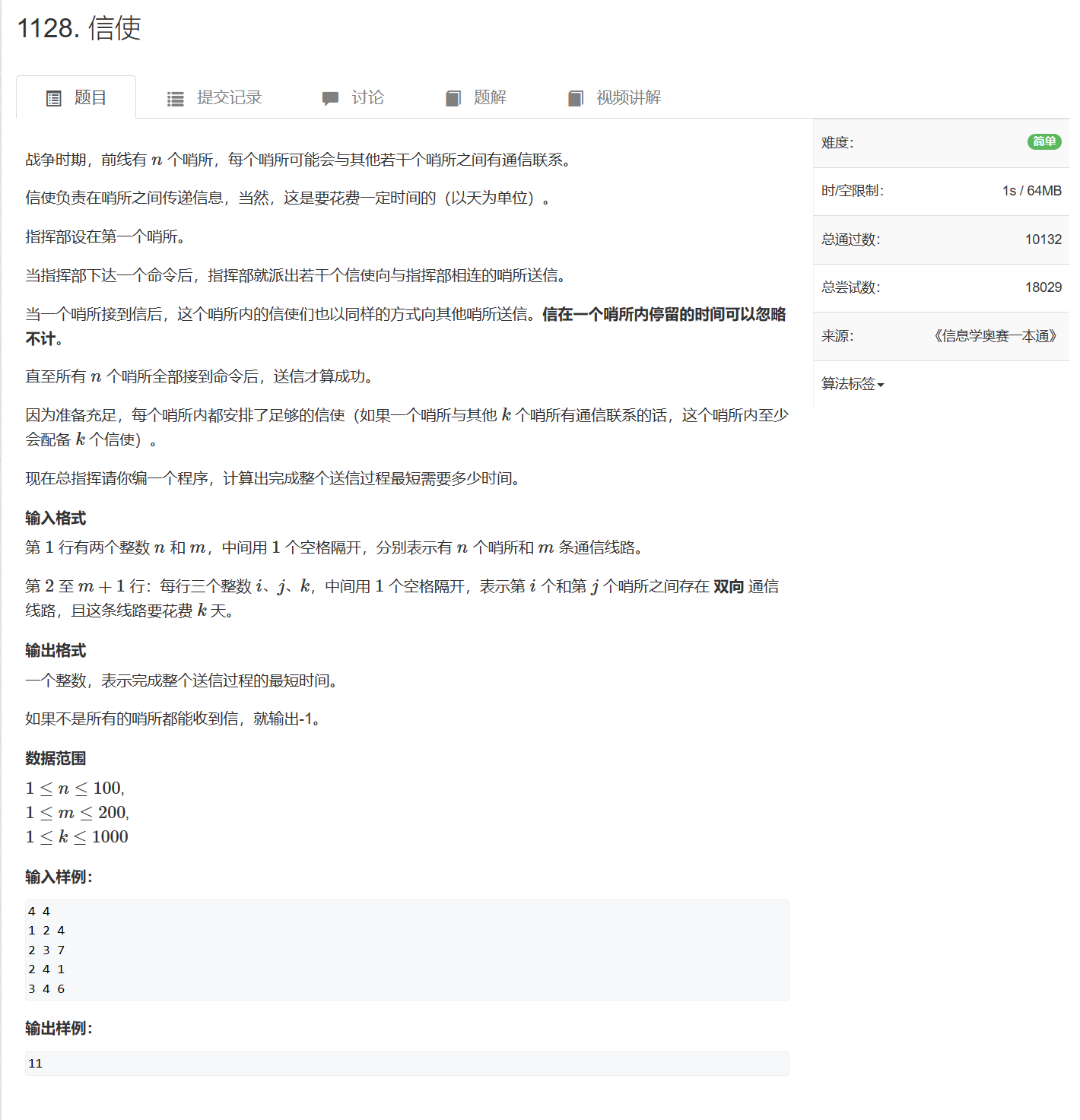
单源最短路,稀疏图,用堆优化Dijkstra即可,最后统计所有dis的最大值并返回即可
// 单源最短路,最后将第1个点到其他点的距离累加即可
// 稀疏图,依然是堆优化的dijkstra
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;typedef pair<int, int> PII;
const int N = 110, M = 410;
int h[N], e[M], ne[M], w[M], idx = 1;
priority_queue<PII, vector<PII>, greater<PII>> q;
int n, m;
bool st[N]; int dis[N];void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void dijkstra()
{memset(dis, 0x3f, sizeof(dis));dis[1] = 0;q.push({0, 1});while (q.size()){auto t = q.top(); q.pop();int x = t.second, d = t.first;if (st[x]) continue;st[x] = true;for (int i = h[x]; i != -1; i = ne[i]) {int y = e[i];if (dis[y] > d + w[i]){dis[y] = d + w[i];q.push({dis[y], y});}}}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);int x, y, d;for (int i = 1; i <= m; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, d), add(y, x, d);}dijkstra();int res = 0;bool flag = true;for (int i = 2; i <= n; ++ i ){if (dis[i] == 0x3f3f3f3f) {flag = false;break;}res = max(res, dis[i]);}if (flag) printf("%d\n", res);else puts("-1");return 0;
}
debug:%d打成了5d,乐,竟然能编译通过
判断某个点的最短距离是否已经确定,打成了if(dis[x]); dis[x] = true,这也debug了半天
1127. 香甜的黄油
1127. 香甜的黄油 - AcWing题库
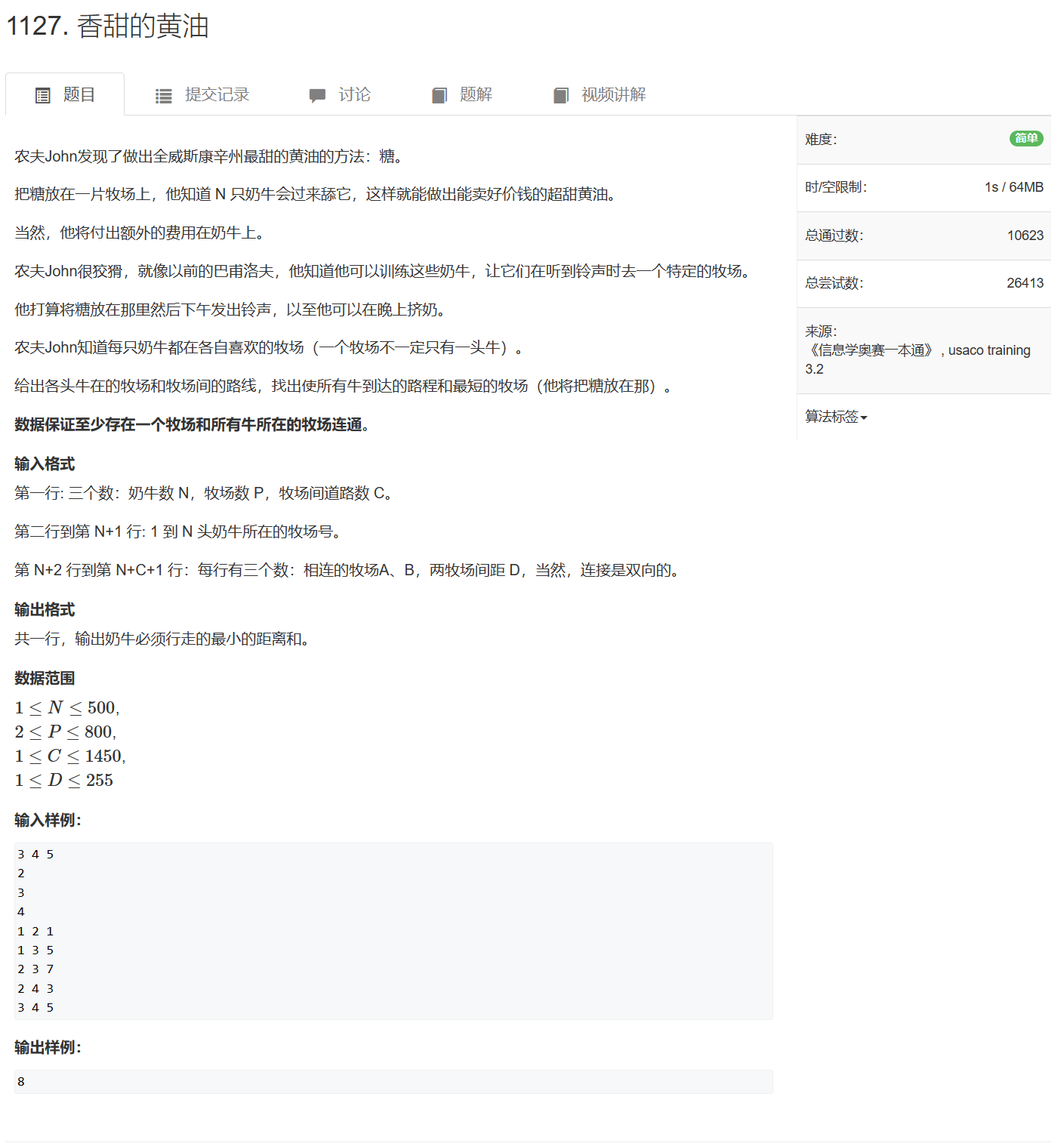
// 多源汇最短路,由于flody可能超时,所以用单源最短路求解
// 这里用spfa
#include <iostream>
#include <cstring>
using namespace std;const int N = 810, M = 3000;
int h[N], e[M], ne[M], w[M], idx = 1;
int dis[N]; bool st[N];
int s, n, m;
int q[N];
int id[N];void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void spfa(int k)
{memset(dis, 0x3f, sizeof(dis));int hh = 0, tt = 1;dis[k] = 0;q[tt ++ ] = k, st[k] = true;while (tt != hh){int x = q[hh ++ ];if (hh == N) hh = 0;st[x] = false;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (dis[y] > dis[x] + w[i]){dis[y] = dis[x] + w[i];if (!st[y]) {q[tt ++ ] = y, st[y] = true;if (tt == N) tt = 0;}}}}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d%d", &s, &n, &m);for (int i = 1; i <= s; ++ i ) scanf("%d", &id[i]);int x, y, d;for (int i = 1; i <= m; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, d), add(y, x, d);}int res = 0x3f3f3f3f;for (int i = 1; i <= n; ++ i ){spfa(i);int sum = 0; bool flag = true;for (int j = 1; j <= s; ++ j ) {if (dis[id[j]] == 0x3f3f3f3f){flag = false;break;}sum += dis[id[j]];}if (flag) res = min(res, sum);}printf("%d\n", res);return 0;
}
用自己写的循环队列代替queue,时间大概快了一倍
需要注意的是,循环队列的hh和tt从0开始使用,并且都是后置++,++后还要维护循环性质
以下是用queue实现的版本
// 多源汇最短路,由于flody可能超时,所以用单源最短路求解
// 这里用spfa
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;typedef long long LL;
const int N = 810, M = 1500 * 2;
int h[N], e[M], ne[M], w[M], idx = 1;
int dis[N]; bool st[N];
int s, n, m;
queue<int> q;
int id[N];void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void spfa(int k)
{memset(dis, 0x3f, sizeof(dis));dis[k] = 0;q.push(k), st[k] = true;while (q.size()){int x = q.front(); q.pop();st[x] = false;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (dis[y] > dis[x] + w[i]){dis[y] = dis[x] + w[i];if (!st[y]) q.push(y), st[y] = true;}}}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d%d", &s, &n, &m);int t;for (int i = 1; i <= s; ++ i ) scanf("%d", &id[i]);int x, y, d;for (int i = 1; i <= m; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, d), add(y, x, d);}LL res = 1e18;for (int i = 1; i <= n; ++ i ){spfa(i);LL sum = 0; bool flag = true;for (int i = 1; i <= s; ++ i ){if (dis[id[i]] == 0x3f3f3f3f) {flag = false;break;}sum += dis[id[i]];}if (flag) res = min(res, sum);}printf("%lld\n", res);return 0;
}
1126. 最小花费
1126. 最小花费 - AcWing题库
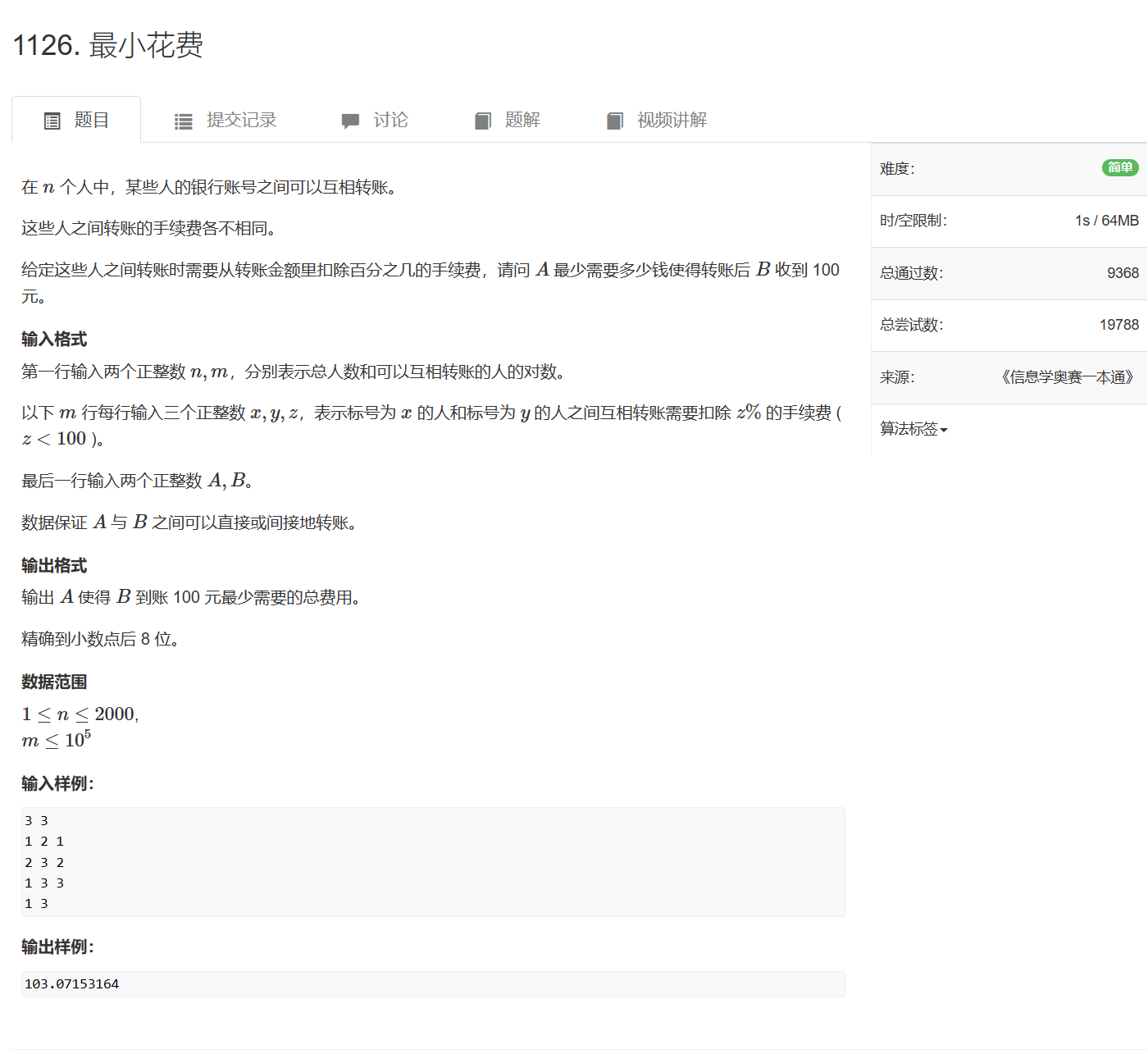
转账金额A,当手续费的比例为z时,只能转账A(1 - z)
若每条边的权值为实际转账的金额比例,那么从起点到终点,这个比例越大,花费的初始金额就越少,所以这题需要找一条从起点到终点比例最大的路径
即从起点到终点经过的所有边的比例相乘最大,由于比例的大小为 0 < z < = 1 0 < z <= 1 0<z<=1,所以这里初始化dis数组以及邻接矩阵为全0
接着用spfa或者dijkstra求“最短路”即可
// 同样的单源最短路,spfa解决#include <iostream>
using namespace std;const int N = 2010;
double g[N][N];
int n, m, start, ed;
double dis[N]; bool st[N];
int q[N], tt, hh;void spfa()
{dis[start] = 1.0;q[tt ++ ] = start, st[start] = true;while (tt != hh){int x = q[hh ++ ];if (hh == N) hh = 0;st[x] = false;for (int j = 1; j <= n; ++ j ){if (dis[j] < dis[x] * g[x][j]){dis[j] = dis[x] * g[x][j];if (!st[j]) {q[tt ++ ] = j, st[j] = true;if (tt == N) tt = 0;}}}}
}int main()
{scanf("%d%d", &n, &m);int x, y, z;for (int i = 1; i <= m; ++ i ){scanf("%d%d%d", &x, &y, &z);g[x][y] = g[y][x] = 1 - (z / 100.0);}scanf("%d%d", &start, &ed);spfa();printf("%.8lf\n", 100 / dis[ed]);return 0;
}
920. 最优乘车
920. 最优乘车 - AcWing题库
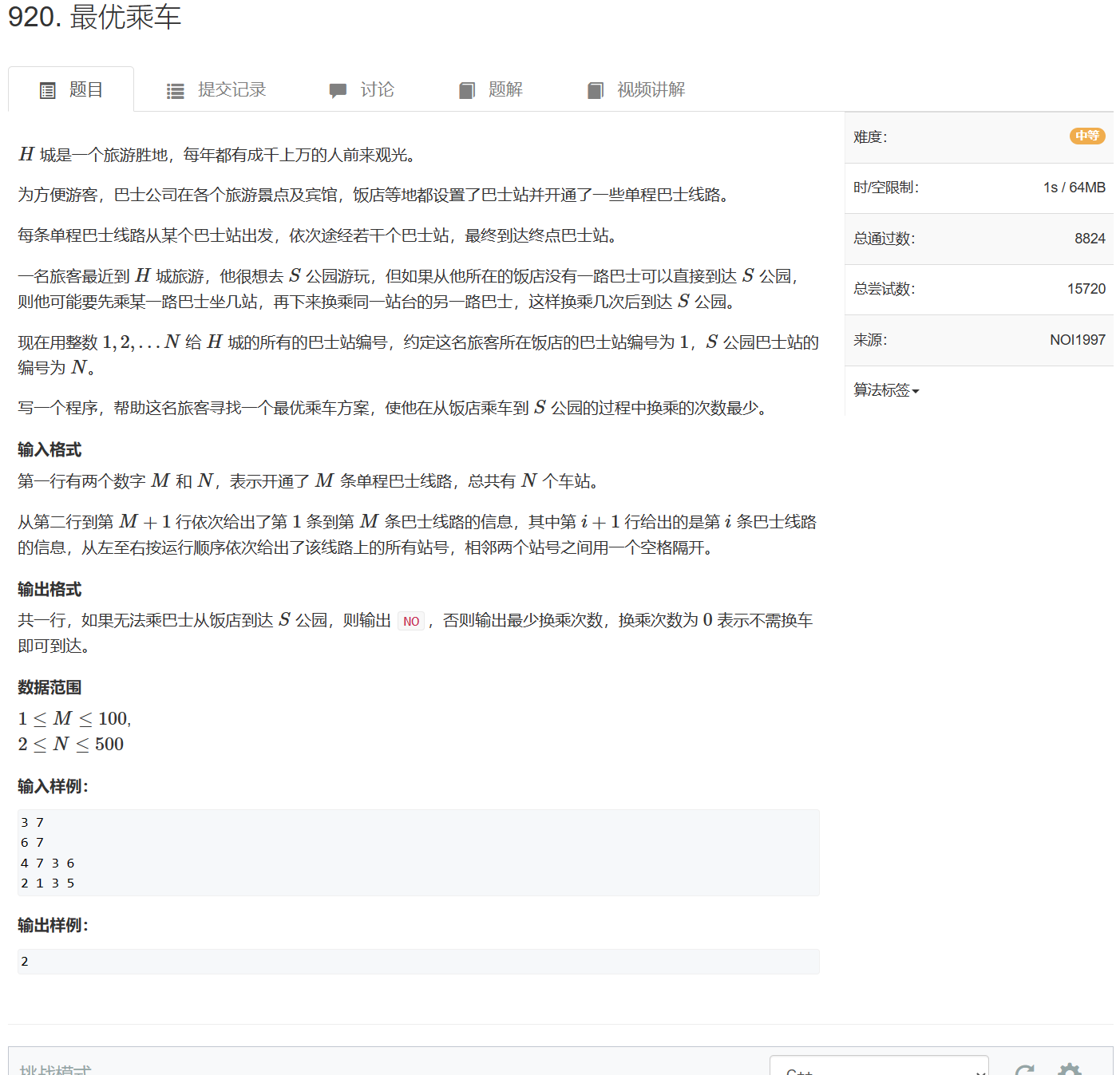
没之前的题目裸,需要一些思考
虽然题目没有给定边的权重,但是给定了公交路线,可知公交路线 a a a中, a i a_i ai到 a j a_j aj的权重为1,表示从i地到j地需要的乘车次数,当如 a i a_i ai在 a a a中的下标要出现在 a j a_j aj之前,这是一张有向图
所以,根据题目给定的公交路线,找出图中所有的有向边,最后用单源最短路就行了
由于边的权值为1,甚至用bfs也行
// 一条路线之间的点可达,存在有向边,线路中有n个点,存在Cn2条边
// 边的权值为1,表示需要乘车的次数,由于权值为1,所以可以用bfs
#include <iostream>
#include <sstream>
#include <string>
#include <cstring>
using namespace std;const int N = 510, M = 11;;
int a[N], g[N][N], q[N];
int dis[N];
int n, m, tt, hh;int bfs()
{dis[1] = 0;q[tt ++ ] = 1;while (tt != hh){int x = q[hh ++ ];if (hh == N) hh = 0;for (int y = 1; y <= n; ++ y ){if (y != x && !dis[y] && g[x][y]) {dis[y] = dis[x] + 1;if (y == n) return dis[y];q[tt ++ ] = y;}}}return 0;
}int main()
{scanf("%d%d", &m, &n);string line;getline(cin, line);for (int i = 0; i < m; ++ i ){getline(cin, line);stringstream s(line);int idx = 0, p;while (s >> p) a[idx ++ ] = p;for (int j = 0; j < idx; ++ j )for (int k = j + 1; k < idx; ++ k )g[a[j]][a[k]] = 1;}int t = bfs();if (t == 0) puts("NO");else printf("%d\n", t - 1);return 0;
}
903. 昂贵的聘礼
903. 昂贵的聘礼 - AcWing题库

以下是我的思路,我只是记录一下不建议看
要获得某个物品,有两种方式:1. 直接购买 2. 在拥有替代品的前提下,以优惠价格购买
此外无法找出其他方法,需要考虑的是:以优惠价格购买时,拥有替代品的代价是什么?
若从正面考虑,假设酋长的10000金币是一个物品,现可以直接购买或者使用替代品。若使用替代品以更低的价格购买,那么购买替代品的价格是多少?同样,购买替代品也有两种方式,是直接购买省钱还是用替代品的替代品购买省钱。这是一个无止尽的过程,什么时候会停止?物品没有替代品时停止,这就意味着我们要递归到最底部后,在向上回溯的过程中,才能计算两种方式中哪种最省钱
这是直接的思路,可能能做出来吧,没试过
正解:
将酋长的10000金币看成物品,并且是有向图的终点。物品之间有什么关系?从一个点走到另一个点,前提是当前点是下一点的替代品,那么从当前点到下一点的代价就是用当前物品购买下一物品的优惠价格
所以边的权重为优惠价格,当前除了以优惠价格购买,还能直接购买。直接购买时,当前点的含义不再是一个物品,所以这里的点是一个虚拟点,到其他点的权重为直接购买的价格
若当前已经购买了物品,走向下一物品时,直接购买的价格肯定比使用替代品高,所以不用设置已经购买物品时,再直接购买其他物品的边。这样的边没有意义
由于存在一些物品无法使用替代品购买,所以只要设置手上没有物品时,直接购买物品的边
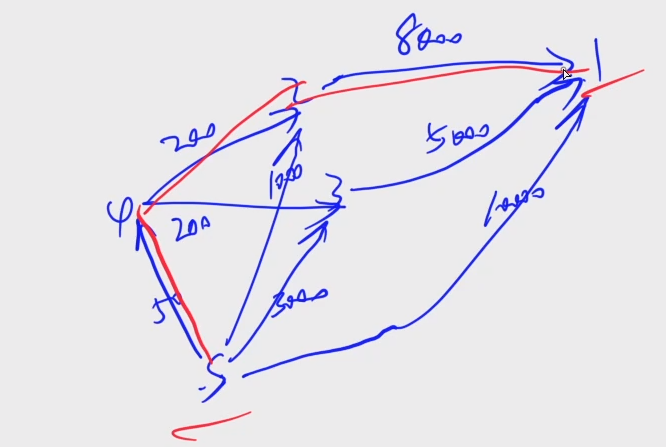
虚拟点为上图的s
起点为s,终点为1号物品(酋长的10000金币),跑一个最短路即可
为什么起点是s?存在一些只能直接购买的物品
最后考虑等级限制,等级差距不超过m的人可以交换物品,由于题目数据量小,可以直接暴力枚举。假设酋长的等级为a,那么需要枚举的区间为 [ a − m , a + m ] [a-m, a+m] [a−m,a+m],枚举这个区间中长度为m的区间,每次枚举跑一次最短路即可
#include <iostream>
#include <cstring>
using namespace std;const int N = 110;
int dis[N], g[N][N];
int level[N];
bool st[N];
int n, m;int dijkstra(int l, int r)
{memset(dis, 0x3f, sizeof(dis));memset(st, false, sizeof(st));dis[0] = 0;for (int i = 0; i <= n; ++ i ){int t = -1;for (int j = 0; j <= n; ++ j)if (!st[j] && (t == -1 || dis[j] < dis[t])) t = j;st[t] = true;for (int j = 1; j <= n; ++ j )if (l <= level[j] && level[j] <= r)dis[j] = min(dis[j], dis[t] + g[t][j]);}return dis[1];
}int main()
{memset(g, 0x3f, sizeof(g));scanf("%d%d", &m, &n);int p, x, t, v;for (int i = 1; i <= n; ++ i ) g[i][i] = 0;for (int i = 1; i <= n; ++ i ){scanf("%d%d%d", &p, &level[i] , &x);g[0][i] = min(g[0][i], p);while ( x -- ){scanf("%d%d", &t, &v);g[t][i] = min(g[t][i], v);}}int res = 0x3f3f3f3f;for (int i = level[1] - m; i <= level[1]; ++ i ){int t = dijkstra(i, i + m);res = min(t, res);}printf("%d\n", res);return 0;
}
1135. 新年好
1135. 新年好 - AcWing题库
先用堆优dijkstra跑单源最短路,一共是6个源点,分别是家所在的点以及亲戚所在的点,保存最短距离
然后dfs爆搜,以1号点为起点,剩下五个点的全排列为搜索顺序,记录全排列中路径的最短距离
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;const int N = 5e5 + 10, M = 2e5 + 10;
const int INF = 1e9;
int h[N], e[M], ne[M], w[M], idx = 1;
int dis[6][N]; bool st[N];
int tar[10];
int n, m;
typedef pair<int, int> PII;
priority_queue<PII, vector<PII>, greater<PII>> q;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void dijkstra(int start, int si) // si为start在dis数组中的一维下标
{memset(st, false, sizeof(st));dis[si][start] = 0;q.push({ 0, start });while (q.size()){auto t = q.top(); q.pop();int x = t.second, d = t.first;if (st[x]) continue;st[x] = true;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (dis[si][y] > d + w[i]){dis[si][y] = d + w[i];q.push({ dis[si][y], y});}}}
}int dfs(int cnt, int si, int d) // cnt为已经拜访的亲戚数量,si为当前所在点在dis数组中的一维下标,d为递达当前点的“距离”
{if (cnt == 5) return d;int res = INF;for (int i = 1; i <= 5; ++ i ){if (!st[i]){int y = tar[i]; // 要访问的下一个点在图中的编号st[i] = true;res = min(res, dfs(cnt + 1, i, d + dis[si][y]));st[i] = false;}}return res;
}int main()
{memset(h, -1, sizeof(h));memset(dis, 0x3f, sizeof(dis));scanf("%d%d", &n, &m);for ( int i = 1; i <= 5; ++ i ) scanf("%d", &tar[i]);int x, y, t;while ( m -- ){scanf("%d%d%d", &x, &y, &t);add(x, y, t), add(y, x, t);}dijkstra(1, 0);for (int i = 1; i <= 5; ++ i ) dijkstra(tar[i], i);memset(st, false, sizeof(st));printf("%d\n", dfs(0, 0, 0));return 0;
}
debug:双向边,M又少开一倍,但是TLE,以后M都开两倍吧,这太难调试了
dfs最后要返回res,因为min要使用dfs的返回值
340. 通信线路
340. 通信线路 - AcWing题库
分析题意:对于每条1~n的路径,我们只要支付第k+1大的边的金额即可。若边的数量少于k+1,那么支付金额为0
所以本题的最短路,短在第k+1大的边权中,最小的那个。所有最大中找最小,自然地想到二分。二分边权,得到ans,使得ans是所有1~n路径中,第k+1大的权值中最小的那个
二分的范围: [ 0 , 1 e 6 + 1 ] [0, 1e6+1] [0,1e6+1],权值最小值-1~权值最大值+1
check:分析ans的性质,所有1~n的路径中,第k+1大的边权中最小值为ans
说明至少存在一条路径,经过了k条边权大于ans的边,即and是这条路径中第k+1大的边
那么其他路径就一定经过了多于k条权值大于ans的边
由此得到check的检查逻辑:根据参数x,判断1~n的所有路径中,是否存在一条路径,经过了小于等于k条的权值大于x的边。若存在返回true,否则返回false
试想一下,x越大,check的性质越容易满足,x越小,性质越难满足
两种特殊情况:ans为0,说明1~n的所有路径中,至少存在一条路径,经过了k条权值大于0的边,那么第k+1条边的权值为0,需要支付金额为0
ans为 1 e 6 + 1 1e6+1 1e6+1,说明1n的所有路径中,至少存在一条路径,经过了k条权值大于$1e6+1$的边,由于边权最大为$1e6$,所以这样的路径是不存在的,即1n之间不连通
如何得知1~n的所有路径中,经过了几条权值大于x的边?
对于权值大于x的边,将其权值设置为1,否则设置为0,跑一遍最短路,就能知道1~n的最短路径经过了几条权值大于x的边
对于权值只有0和1的最短路问题,可以用双端队列bfs
#include <iostream>
#include <cstring>
#include <deque>
using namespace std;const int N = 1010, M = 20010;
int n, p, k;
int h[N], e[M], ne[M], w[M], idx = 1;
int dis[N]; bool st[N];
deque<int> q;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}bool check(int bound)
{memset(dis, 0x3f, sizeof(dis));memset(st, false, sizeof(st));dis[1] = 0;q.push_back(1);while (q.size()){int x = q.front(); q.pop_front();if (st[x]) continue;st[x] = true;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i], d = w[i] > bound;if (dis[y] > dis[x] + d){dis[y] = dis[x] + d;if (d) q.push_back(y);else q.push_front(y);}}}return dis[n] <= k;
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d%d", &n, &p, &k);int x, y, d;while ( p -- ){scanf("%d%d%d", &x, &y, &d);add(x, y, d), add(y, x, d);}int l = 0, r = 1e6 + 1;while ( l < r ){int mid = l + r >> 1;if (check(mid)) r = mid;else l = mid + 1;}if (l == 1e6 + 1) puts("-1");else printf("%d\n", l);return 0;
}
342. 道路与航线
342. 道路与航线 - AcWing题库
直接用spfa会被卡两个数据
根据题意:道路,双向边,存在环,正权;航线:单向边,无环,负权
其中关于是否有环以及权值的正负是选择算法的关键
若图中没有负权边,直接用堆d
若图中无环,直接按照拓扑序遍历所有点就能确定最短路
结合以上两者,可以得到以下算法:
将所有点根据道路的连通性分成多个连通块,每个连通块之间不连通
连通每个连通块的是航线,单向边。读取所有的航线后,按照拓扑序遍历每个连通块,对于每个连通块,跑堆d求最短路
用id数组表示每个点所属的连通块编号,用二维数组blocks存储每个连通块中点的编号
读入所有道路后,dfs可以遍历连通块中的所有点,维护出id和blocks数组信息
读入所有航线,维护出in数组,计算所有点的入度后按照拓扑序跑堆d
// 道路是双向的,航线单向,可能是负数也可能是正数
// 并且图中保证不会存在环路
// 直接spfa?
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;typedef pair<int, int> PII;
const int N = 3e4, M = 2e5;
int h[N], e[M], ne[M], w[M], idx = 1;
int n, p, r, s;
int dis[N]; bool st[N];
int id[N], cnt, in[N];
vector<int> blocks[N];
queue<int> q;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void dfs(int x)
{id[x] = cnt;blocks[cnt].push_back(x);for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!id[y]) dfs(y);}
}void dijkstra(int k)
{priority_queue<PII, vector<PII>, greater<PII>> hp;for (auto x : blocks[k]) hp.push({ dis[x], x });while (hp.size()){auto t = hp.top(); hp.pop();int x = t.second, d = t.first;if (st[x]) continue;st[x] = true;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (id[x] != id[y] && -- in[id[y]] == 0) q.push(id[y]);if (dis[y] > d + w[i]){dis[y] = d + w[i];if (id[x] == id[y]) hp.push( {dis[y], y });}}}
}void topsort()
{memset(dis, 0x3f, sizeof(dis));dis[s] = 0;for (int i = 1; i <= cnt; ++ i )if (!in[i]) q.push(i);while (q.size()){int x = q.front(); q.pop(); // 连通块iddijkstra(x);}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d%d%d", &n, &r, &p, &s);int x, y, d;for (int i = 0; i < r; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, d), add(y, x, d);}for (int i = 1; i <= n; ++ i ){if (!id[i]) {cnt ++ ;dfs(i); // 维护出i所在的连通块}}for (int i = 0; i < p; ++ i ){scanf("%d%d%d", &x, &y, &d);add(x, y, d);in[id[y]] ++ ;}topsort();for (int i = 1; i <= n; ++ i ) {if (dis[i] >= 0x3f3f3f3f / 2) puts("NO PATH");else printf("%d\n", dis[i]);}return 0;
}
341. 最优贸易
341. 最优贸易 - AcWing题库

状态表示:
集合:所有从1~n的路径,用分界点将这些路径一分为二
属性:在分界点之前(包括分界点)买入 - 在分界点(包括分界点)之后能卖出的最大价值,即最大卖出价值 - 最小买入价值
f ( i ) f(i) f(i)表示以i号点为分界点的1~n路径中,可以赚取的最大价值
状态划分:分界点从1~n,此时划分的子集不遗漏地组成了整个集合(虽然有重复,但是题目要求最优解,重复的情况不影响最优解)
如何求路径中的前半段最小值 d m i n ( k ) dmin(k) dmin(k)?
若与k直接相连的点有t个,那么 d m i n ( k ) = m i n ( d m i n ( s 1 ) , d m i n ( s 2 ) , . . . d m i n ( s t ) , w k ) dmin(k) = min(dmin(s_1), dmin(s_2), ... dmin(s_t), w_k) dmin(k)=min(dmin(s1),dmin(s2),...dmin(st),wk)
走到k的最小值就等于从所有走到与k直接相连的点的最小值以及自己的权值中的最小值
由于这些状态依赖可能存在环,即当dp推导出的状态不是最优解,所以这里用最短路求这些状态
最短路用dijkstra或者spfa,是否能用dijkstra?由于在最短路问题中,当前点的最短路径由与之相连的所有点的最短路径累加上自己的权值确定,并且权值只能是正的
根据这个性质,已经确定最短路的点在之后的更新中不可能出现更短的路径
虽然这题的边权为正,但是这题的状态不是由之前的状态累加,而是从之前的状态中取min或者max,这就导致dijkstra每次的更新无法求得最优解,需要后续的再次更新,此时的时间复杂度无法保证,这是最关键的,所以不使用dijkstra
那spfa呢?spfa是bellman-ford的优化,bellman根据边的数量进行更新,每次更新所有边
所以bellman能够保证最短路的边数,即时间复杂度是确定的,所以可以使用sfpa
用sfpa跑出dmin和dmax数组的信息,分别存储了从1到k的最小值,以及从k到n的最大值
由于从k到n的起点是变化的,但是终点不变,所以这里可以建一张反向图,以n为起点,更新dmax
#include <iostream>
#include <cstring>
using namespace std;const int N = 1e5 + 10, M = 2e6;
int w[N];
int hs[N], ht[N], e[M], ne[M], idx;
int dmin[N], dmax[N]; bool st[N];
int n, m;
int q[N];void spfa(int h[], int dis[], int t)
{int tt = 0, hh = 0;if (t == 1){memset(dis, 0x3f, sizeof(dmin));q[tt ++ ] = 1; st[1] = true;dis[1] = w[1];}else{memset(dis, -0x3f, sizeof(dmax));q[tt ++ ] = n; st[n] = true;dis[n] = w[n];}while (tt != hh){int x = q[hh ++ ];if (hh == N) hh = 0;st[x] = false;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if ((t == 1 && dis[y] > min(dis[x], w[y])) || (t == 2 && dis[y] < max(dis[x], w[y]))){if (t == 1) dis[y] = min(dis[x], w[y]);else dis[y] = max(dis[x], w[y]);if (!st[y]) {st[y] = true, q[tt ++ ] = y;if (tt == N) tt = 0;}}}}
}void add(int h[], int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}int main()
{memset(hs, -1, sizeof(hs));memset(ht, -1, sizeof(ht));scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++ i ) scanf("%d", &w[i]);int x, y, t;while ( m -- ){scanf("%d%d%d", &x, &y, &t);add(hs, x, y), add(ht, y, x);if (t == 2) add(hs, y, x), add(ht, x, y);}spfa(hs, dmin, 1);spfa(ht, dmax, 2);int res = 0;for (int i = 1; i <= n; ++ i ){res = max(res, dmax[i] - dmin[i]);}printf("%d\n", res);return 0;
}
相关文章:

第三章 图论 No.1单源最短路及其综合应用
文章目录 1129. 热浪1128. 信使1127. 香甜的黄油1126. 最小花费920. 最优乘车903. 昂贵的聘礼1135. 新年好340. 通信线路342. 道路与航线341. 最优贸易 做乘法的最短路时,若权值>0,只能用spfa来做,相等于加法中的负权边 1129. 热浪 1129.…...
❤ npm不是内部或外部命令,也不是可运行的程序 或批处理文件
❤ npm不是内部或外部命令,也不是可运行的程序 或批处理文件 cmd或者终端用nvm 安装提示: npm不是内部或外部命令,也不是可运行的程序或批处理文件 原因(一) 提示这个问题,有可能是Node没有安装,也有可能是没有配置…...

关于Godot游戏引擎制作流水灯
先上核心代码 游戏节点 流水灯的通途可以是 1. 装饰 2. 音乐类多媒体程序(如FL中TB-303的步进灯) FL Studio Transistor Bass...

C语言 函数指针详解
一、函数指针 1.1、概念 函数指针:首先它是一个指针,一个指向函数的指针,在内存空间中存放的是函数的地址; 示例: int Add(int x,int y) {return xy;} int main() {printf("%p\n",&Add);…...
LNMP及论坛搭建
安装 Nginx 服务 systemctl stop firewalld systemctl disable firewalld setenforce 0 1.安装依赖包 #nginx的配置及运行需要pcre、zlib等软件包的支持,因此需要安装这些软件的开发包,以便提供相应的库和头文件。 yum -y install pcre-devel zlib-devel…...
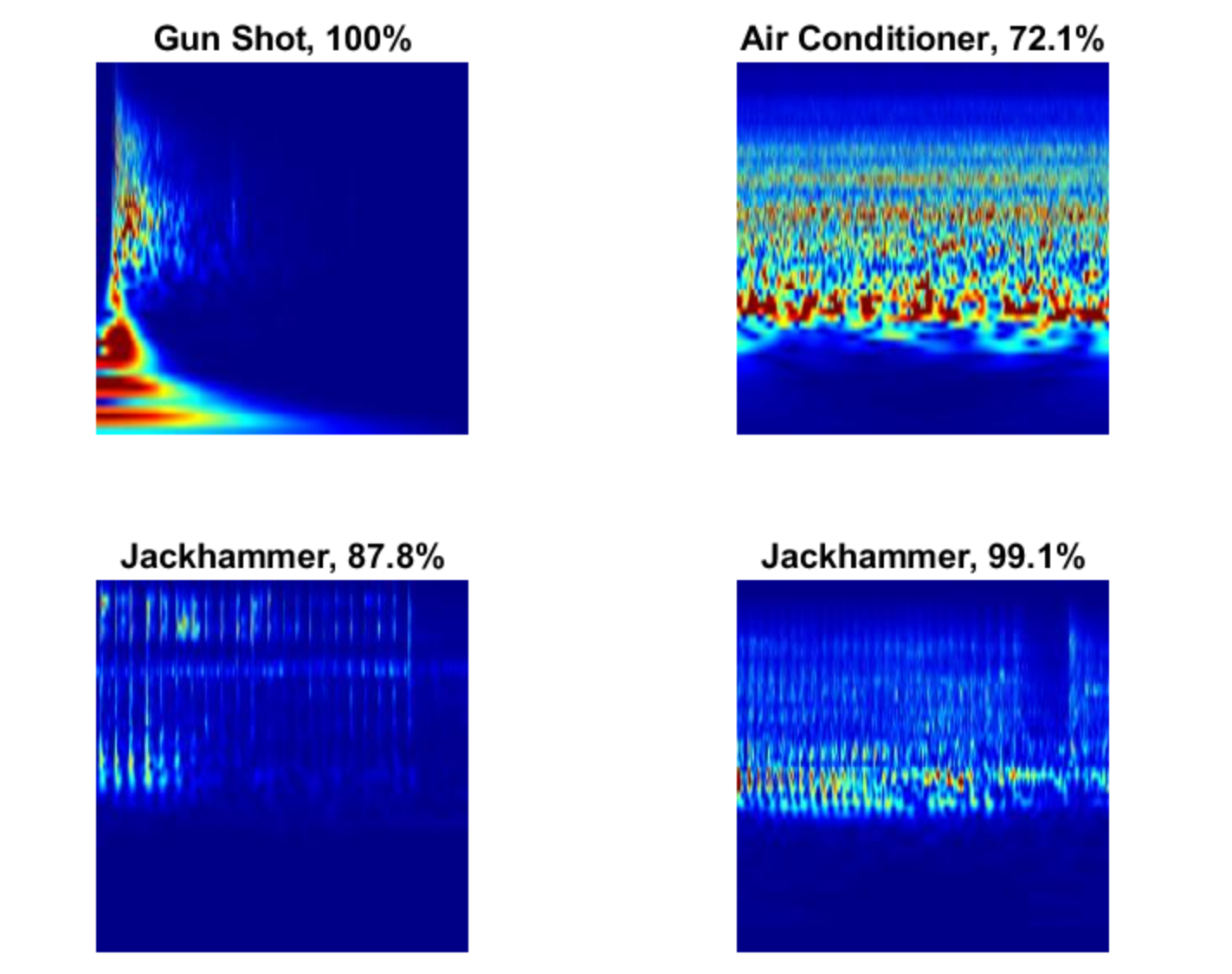
【使用机器学习和深度学习对城市声音进行分类】基于两种技术(ML和DL)对音频数据(城市声音)进行分类(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
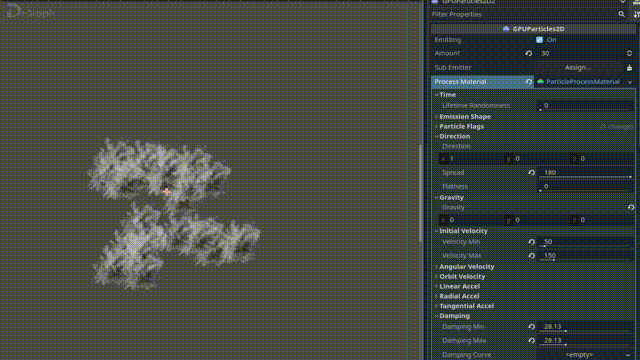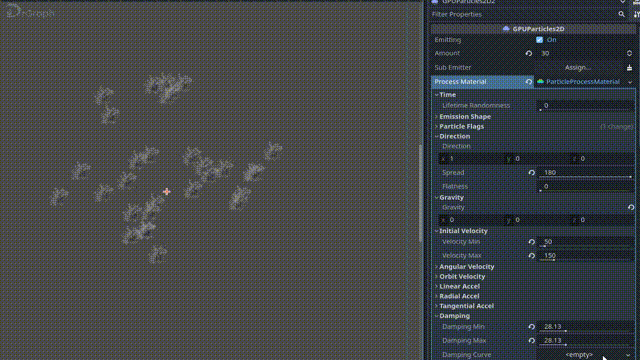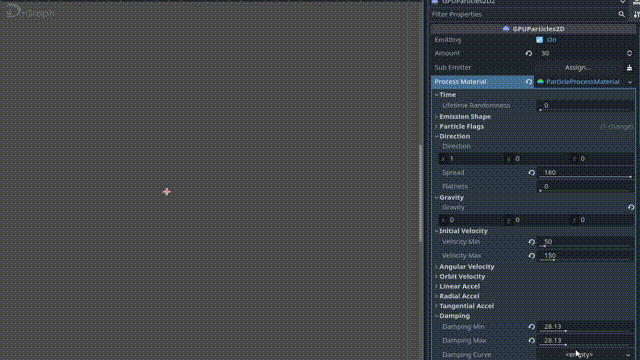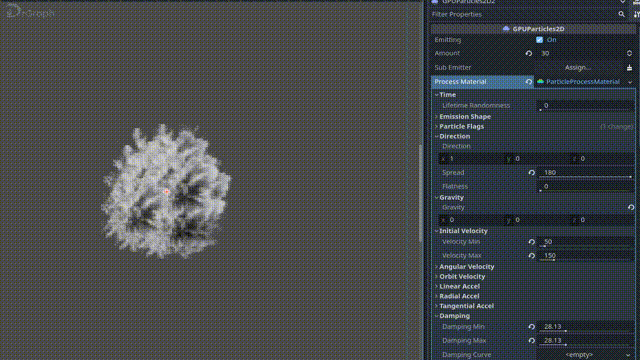
Godot 4 练习 - 制作粒子
演示项目dodge_the_creeps中,有一个Trail,具体运行效果 想要看看咋实现的,看完也不清晰,感觉是要设置某些关键的属性 ChatGPT说:以下是一些重要的属性: texture:用于渲染粒子的纹理。您可以使用…...

Java基础继承详解
Java基础继承详解 在Java中,继承是面向对象编程中的一个重要概念。通过继承,一个类可以从另一个类继承属性和方法,使代码重用和扩展更加方便。下面是关于Java基础继承的一些详解: 关键字: 使用extends关键字可以在一个…...

如何维护你的电脑:打造IT人的重要武器
文章目录 方向一:介绍我的电脑方向二:介绍我的日常维护措施1. 定期清理和优化2. 保持良好的上网习惯和安全防护3. 合理安排软件和硬件的使用4. 数据备份和系统还原 方向三:推荐的维护技巧1. 数据分区和多系统安装2. 内部清洁和散热优化3. 安全…...

【雕爷学编程】MicroPython动手做(31)——物联网之Easy IoT 3
1、物联网的诞生 美国计算机巨头微软(Microsoft)创办人、世界首富比尔盖茨,在1995年出版的《未来之路》一书中,提及“物物互联”。1998年麻省理工学院提出,当时被称作EPC系统的物联网构想。2005年11月,国际电信联盟发布《ITU互联网…...

Elasticsearch 快照和恢复
文章目录 简介快照存储库说明创建或更新存储库接口说明路径参数查询参数请求正文 使用 fs 方式创建存储库验证储存库获取存储库信息删除存储库清理储存库 快照创建快照路径参数查询参数请求正文示例 获取快照查询参数示例 克隆快照查询参数示例 获取快照状态示例 恢复快照查询参…...
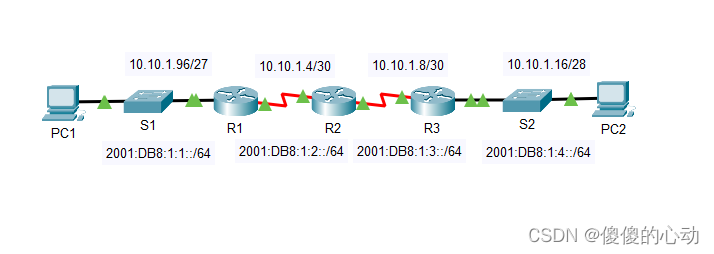
Packet Tracer - 检验 IPv4 和 IPv6 编址
Packet Tracer - 检验 IPv4 和 IPv6 编址 地址分配表 设备 接口 IPv4 地址 子网掩码 默认网关 IPv6 地址/前缀 R1 G0/0 10.10.1.97 255.255.255.224 N/A 2001:DB8:1:1::1/64 N/A S0/0/1 10.10.1.6 255.255.255.252 N/A 2001:DB8:1:2::2/64 N/A 本地链路 F…...

PHP8的表达式-PHP8知识详解
表达式是 PHP 最重要的基石。在 PHP8中,几乎所写的任何东西都是一个表达式。简单但却最精确的定义一个表达式的方式就是"任何有值的东西"。 最基本的表达式形式是常量和变量。当键入"$a 5",即将值"5"分配给变量 $a。&quo…...

亚马逊云科技七项生成式AI新产品生成式AI,为用户解决数据滞后等难题
7月27日,亚马逊云科技在纽约峰会上一连发布了七项生成式AI创新,涵盖了从底层硬件到工具、软件、再到生态的全方位更新,成为它在该领域迄今最全面的一次升级展示,同时也进一步降低了生成式AI的使用门槛。 亚马逊云科技凭借自身端到…...

图片等比例显示全部,兼容不同宽高比例图片
功能描述:预览瀑布流图片 点击预览不同的尺寸图片 <!-- 预览页面 --><div class"sea"><img :src"seaobj.url" alt""></div> .sea {z-index: 100;position: fixed;top: 0;text-align: center;background-colo…...
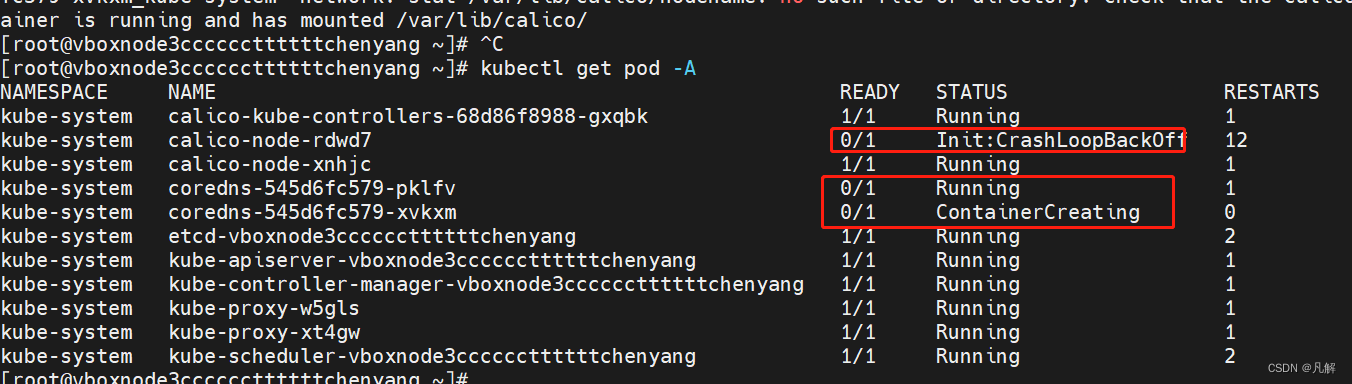
·[K8S:使用calico网络插件]:解决集群节点NotReady问题
文章目录 一:安装calico:1.1:weget安装Colico网络通信插件:1.2:修改calico.yaml网卡相关配置:1.2.1:查看本机ip 网卡相关信息:1.2.2:修改calico.yaml网卡interface相关信…...
泊松损坏图像的快速尺度间小波去噪研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

服务器端开发-golang dlv 远程调试
1。需要root权限的服务器代码调试 sudo ./appps to get piddlv attach pid --headless --listen:40000 --api-version2 --accept-multiclientattach the golang IDE or other IDE 2。不需要root权限的服务器代码调试,另一种选择 dlv --listen:40000 --headlesstr…...

STM32F103——时钟配置
目录 1、认识时钟树 1.1 什么是时钟树 1.2 时钟系统解析 1.2.1 时钟源 1.2.2 锁相环PLL 1.2.3 系统时钟SYSCLK 1.2.4 时钟信号输出MCO 2、如何修改主频 2.1 STM32F1时钟系统配置 2.2 STM32F1 时钟使能和配置 下列进行举例的开发板是原子哥的战舰开发板STM32F103ZET…...

【Linux】信号捕捉
目录 信号捕捉1.用户态与内核态1.1关于内核空间与内核态:1.2关于用户态与内核态的表征: 2.信号捕捉过程 信号捕捉 1.用户态与内核态 用户态:执行用户代码时,进程的状态 内核态:执行OS代码时,进程的状态 …...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
