【C++从0到王者】第十六站:stack和queue的使用
文章目录
- 一、stack的使用
- 1.stack的介绍
- 2.stack的使用
- 二、queue的使用
- 1.queue的护额晒
- 2.queue的使用
- 三、stack和queue相关算法题
- 1.最小栈
- 2.栈的压入、弹出序列
- 3.逆波兰表达式
- 4.两个栈实现一个队列
- 5.用两个队列实现栈
- 6.二叉树的层序遍历
- 1.双队列
- 2.用一个变量levelSize去控制
- 7.二叉树的层序遍历Ⅱ
一、stack的使用
1.stack的介绍

栈是一种容器适配器,专门设计用于在 LIFO 上下文中操作(后进先出),其中元素只从容器的一端插入和提取。
栈被实现为容器适配器,这些类使用特定容器类的封装对象作为其底层容器,提供一组特定的成员函数来访问其元素。 元素从特定容器的“后端”被推入/弹出,这被称为栈的顶部。
底层容器可以是任何标准的容器类模板,也可以是其他一些专门设计的容器类。容器应该支持以下操作:empty、size、back、push_back、pop_front
标准容器类 vector、deque 和 list 满足这些要求。默认情况下,如果没有为特定的堆栈类实例化指定容器类,则使用标准容器 deque。
这里我们需要知道的是,Container适配器就是一个现有的容器进行的一个转换
也就是说,适配器的本质就是一种复用
2.stack的使用
我们先看stack的接口有哪些
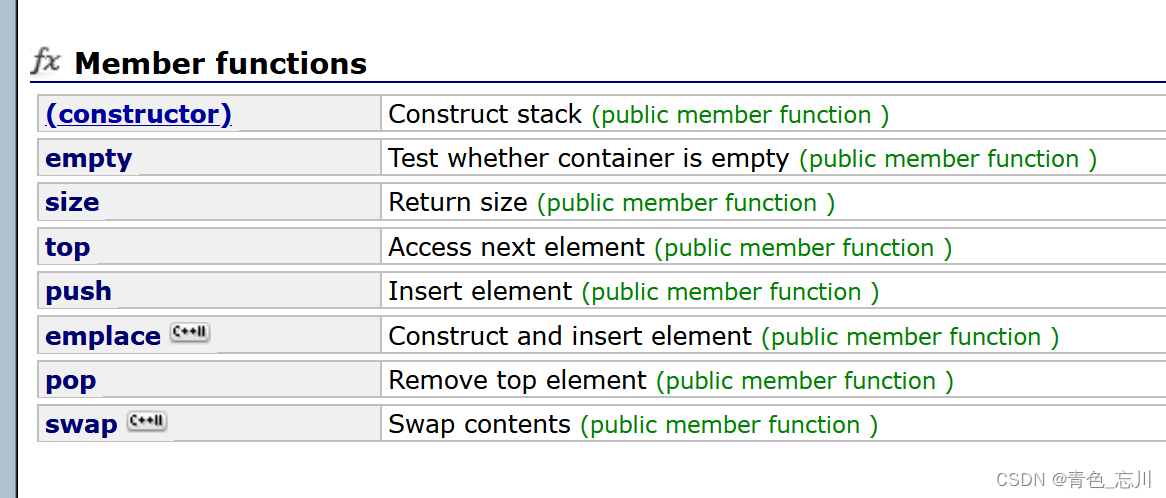
如上所示,这里其实我们一看就已经猜出了七七八八了。因为与前面是string、vector、list是十分相似的。只要结合它的先进先出的特性,我们就知道每个函数都是什么意思了。
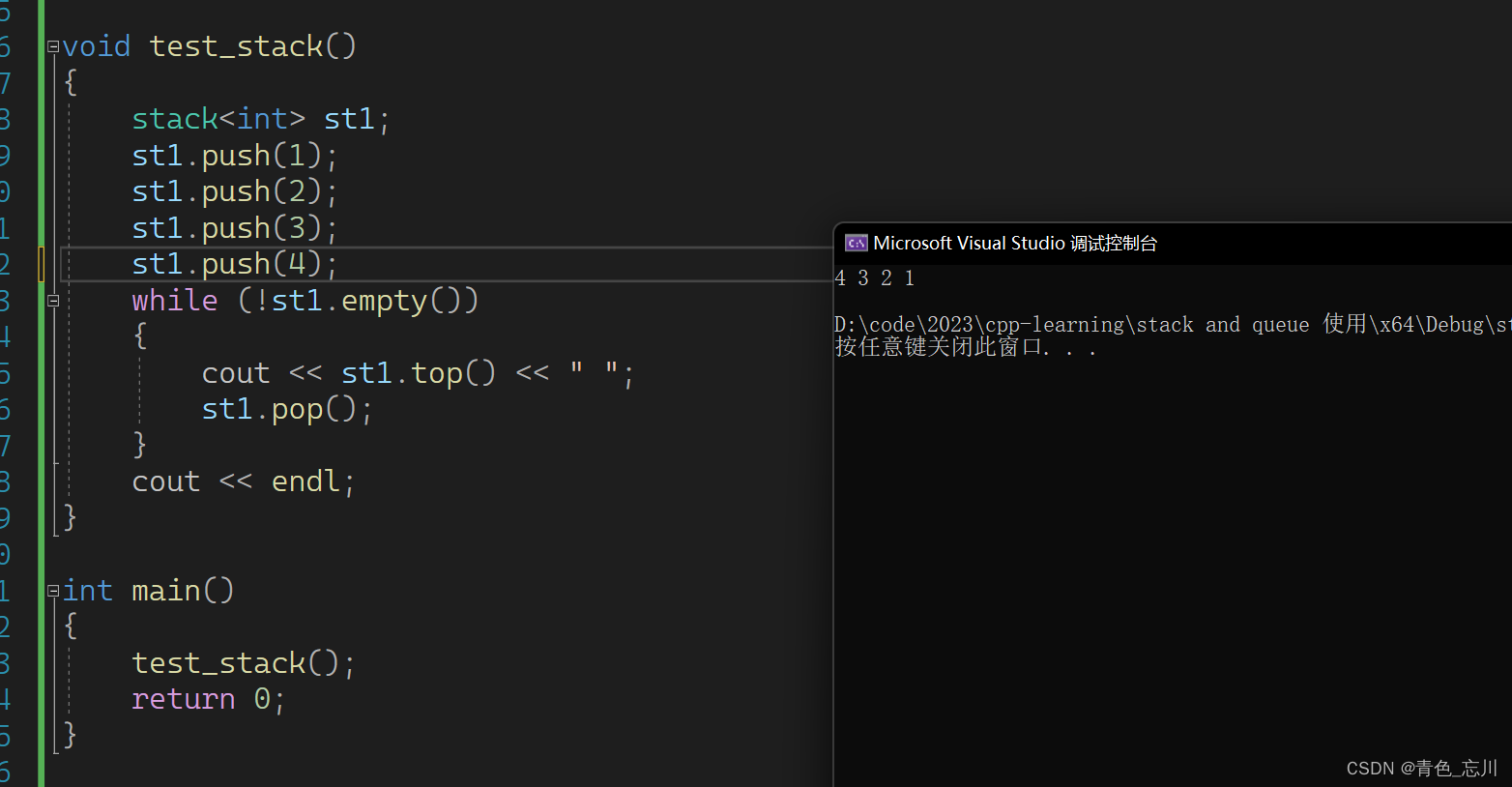
对于stack的使用是非常简单的
void test_stack()
{stack<int> st1;st1.push(1);st1.push(2);st1.push(3);st1.push(4);while (!st1.empty()){cout << st1.top() << " ";st1.pop();}cout << endl;
}
二、queue的使用
1.queue的护额晒

队列是一种容器适配器,专门设计用于在FIFO上下文中操作(先进先出),其中将元素插入容器的一端并从另一端提取。
队列是作为容器适配器实现的,容器适配器是使用特定容器类的封装对象作为其底层容器的类,提供一组特定的成员函数来访问其元素。元素被推入特定容器的“后面”,并从其“前面”弹出。
底层容器可以是标准容器类模板之一,也可以是其他专门设计的容器类。该底层容器应至少支持以下操作:empty、size、front、back、push_back、pop_back。
标准容器类deque和list满足这些要求。默认情况下,如果没有为特定队列类实例化指定容器类,则使用标准容器队列。
2.queue的使用
同样的,我们先来看queue的接口有哪些

在这些接口中,和stack是类似的,只要我们知道了queue的特性是先进先出。我们就能很轻松的推测出每个接口的意思
对于queue的使用是很简单的
void test_queue()
{queue<int> q;q.push(1);q.push(2);q.push(3);q.push(4);while (!q.empty()){cout << q.front() << " ";q.pop();}cout << endl;
}

三、stack和queue相关算法题
1.最小栈
题目链接:最小栈
题目解析:在这道题中,我们为了模拟这种情况,我们可以在成员变量中定义两个栈,一个栈作为正常的出入数据使用,一个栈用来存储最小值。
首先是构造函数,由于我们的成员变量都是自定义类型,所以会自动调用他们的默认构造函数,即他们也会走初始化列表,所以默认构造函数我们是可以直接不用管的。甚至于我们可以直接删掉题目给的构造函数,因为我们不写,编译器自己生成一个。
其次我们的大逻辑是这样的,当我们最小栈为空的时候,我们的最小栈是需要入一个数据的,当我们将要插入的元素是小于等于最小栈要插入的元素的时候,我们会将这个元素给入最小栈
当我们pop的时候,我们也是同理的,如果我们要删除的数据等于最小栈的栈顶元素,那么就也要删除最小栈的栈顶元素。
class MinStack {
public:MinStack(){}void push(int val) {st.push(val);if(min.empty()||(val<=min.top())){min.push(val);}}void pop() {int val=st.top();st.pop();if(val==min.top()){min.pop();}}int top() {return st.top();}int getMin() {return min.top();}
private:stack<int> st;stack<int> min;
};/*** Your MinStack object will be instantiated and called as such:* MinStack* obj = new MinStack();* obj->push(val);* obj->pop();* int param_3 = obj->top();* int param_4 = obj->getMin();*/
2.栈的压入、弹出序列
题目链接:栈的压入弹出序列
题目解析:我们可以使用一个栈来模拟它的入栈出栈逻辑,只要顺着它的思路最终我们的这个栈是空栈的话,那么就说明是匹配的,否则不匹配
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param pushV int整型vector * @param popV int整型vector * @return bool布尔型*/bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {// write code herestack<int> st;int n=pushV.size();int j=0;for(int i=0;i<n;i++){st.push(pushV[i]);while(!st.empty() && st.top()==popV[j]){st.pop();j++;} }return st.empty();}
};
3.逆波兰表达式
题目链接:逆波兰表达式
再谈这道题之前,我们应该先知道什么是逆波兰表达式,我们正常的都是中缀表达式,即3+2*5这种的,都被称之为中缀表达式。
而中缀表达式在计算机中是很难进行运算的。我们需要先将其转换为后缀表达式,前文所说的中缀表达式转化为后缀表达式后应该为3 2 5 * +。后缀表达式的特点就是操作数的顺序不变,而操作符的顺序按照优先级进行了重排。
我们先来看一下后缀运算符是如何进行运算的:
- 操作数入栈
- 如果是操作符,取出栈顶的两个元素进行计算,计算结果放入栈中
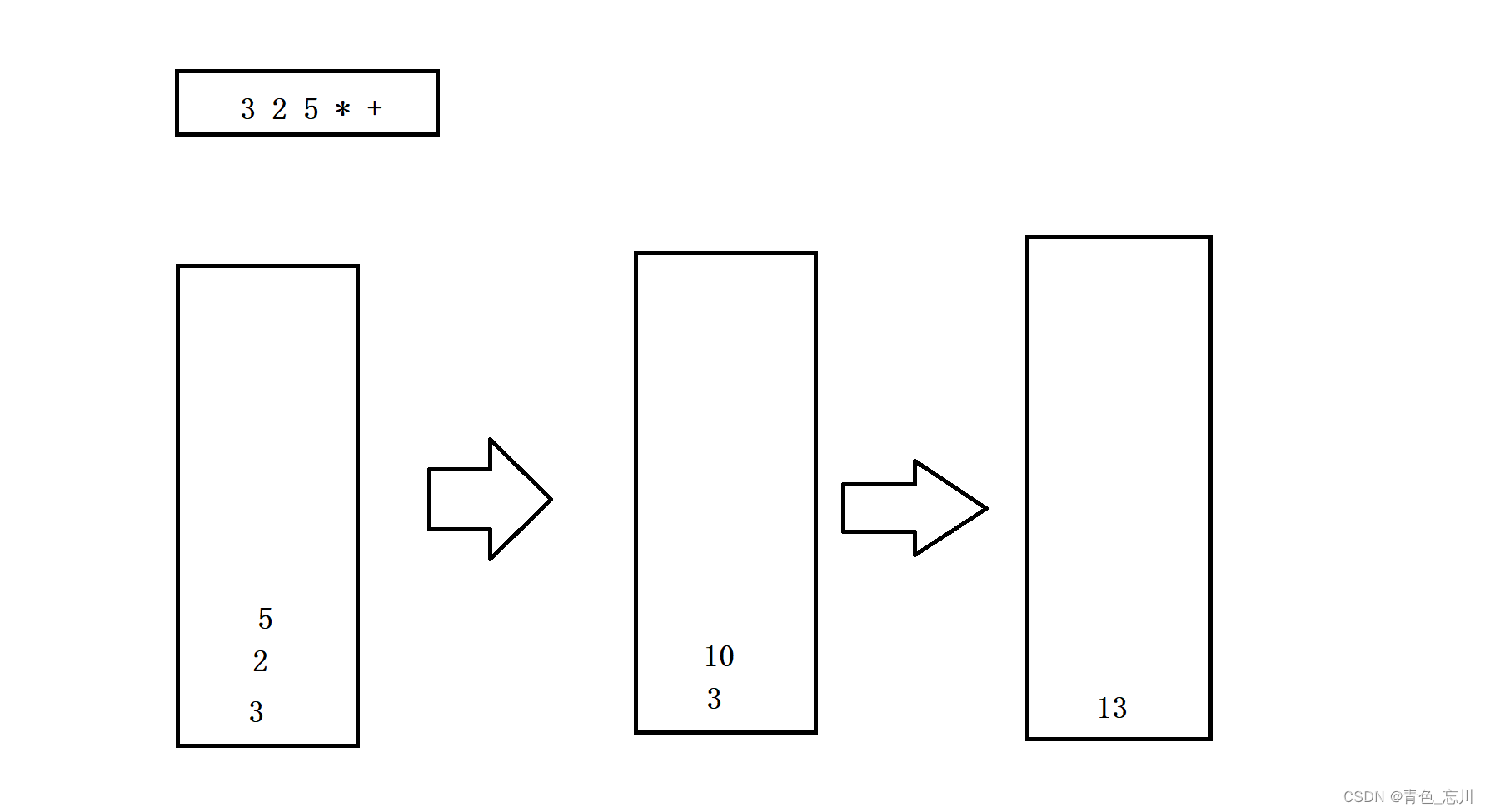
那么如何使得中缀转为后缀呢?
- 操作数输出(即将操作数放到一个容器中)
- 操作符入栈 : ①栈为空,当前操作符比栈顶的优先级高,继续入栈 ②栈不为空,且当前操作符比栈顶的优先级低或者相等,则输出栈顶操作符(因为运算符的优先级只与它相邻的操作符有关,是相对的,如果后面出现了一个更高的操作符,我们无法确定后面是否还有更高的操作符,反而是如果有一个相对较低的操作符,那么前两个肯定是可以进行运算的)
- 表达式结束后,依次出栈顶的操作符
- 注意,有可能会在转换的中间出现连续出操作符的情况,即栈里面已经存储了好几个运算符了,下面的一个运算符要比好几个都要低,就要连续出好几个运算符
比如说2+4-1*3,这个中缀表达式,按照上面的规则可以化为
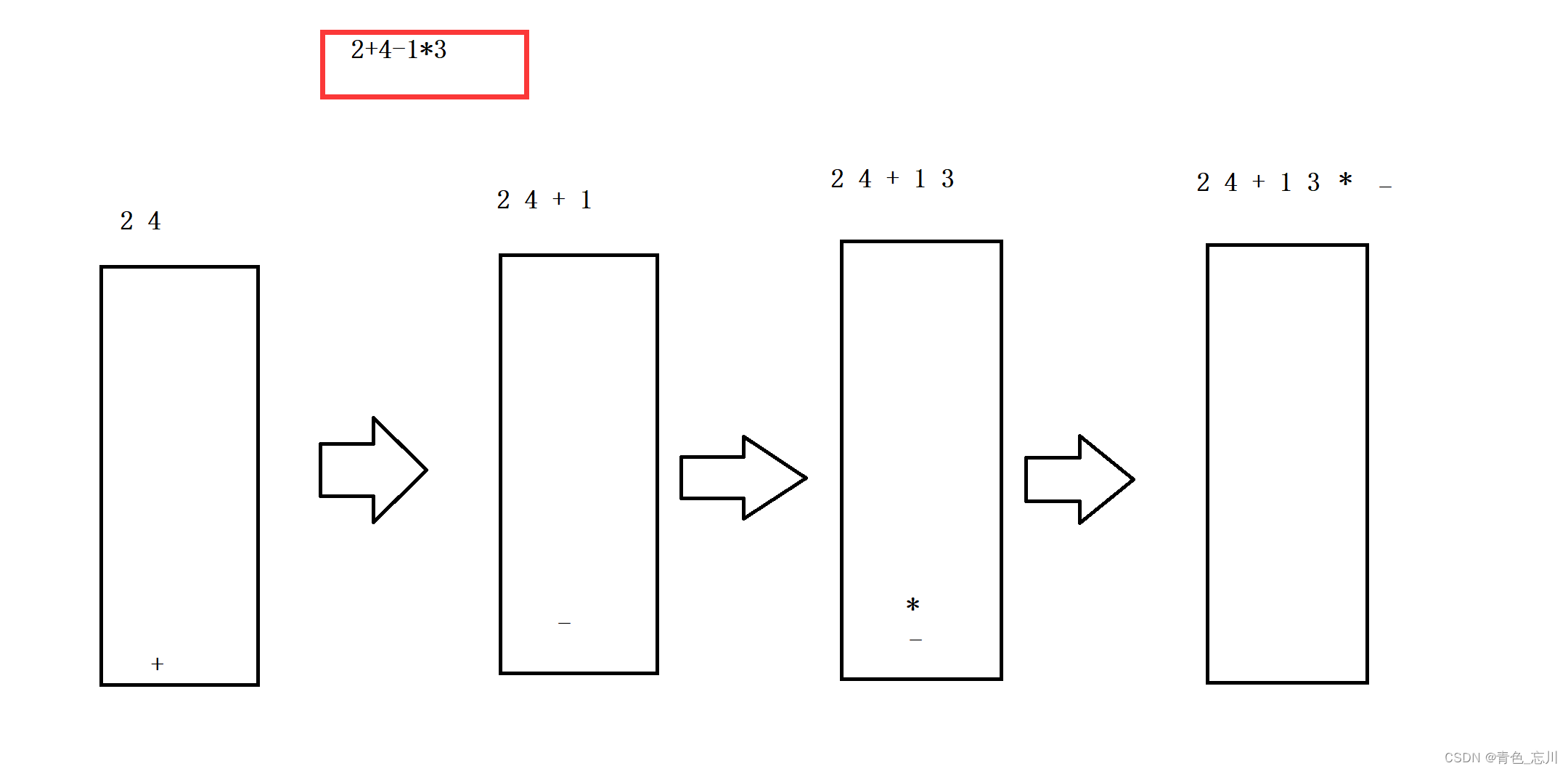
上面都是正常情况的下的处理,但是还有时候会出现括号的影响。
这里可以考虑加上一个特殊标记,当我们这个标记生效时,就代表进入括号内了。或者在这里走一个递归也是可以的。递归的方法就是在遇到括号的时候,我们将括号里面的运算符就需要放入一个新的栈中了。相当于我们只需要让括号返回一个结果就可以了。但是数据还是输出在原来的顺序表中的
我们在回过头来看这道题,我们有了上面的分析,就很容易写出下面代码了。
class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> st;for(auto& str : tokens){if(str=="+"||str=="-"||str=="*"||str=="/"){int right=st.top();st.pop();int left=st.top();st.pop();switch(str[0]){case '+':st.push(left+right);break;case '-':st.push(left-right);break;case '*':st.push(left*right);break;case '/':st.push(left/right);break;}}else{st.push(stoi(str));}}return st.top();}
};
4.两个栈实现一个队列
题目链接:两个栈实现一个队列
对于这个题,我们在之前也已经做过一次分析了,只不过上一次是用C语言手撕了一个栈来实现了。而现在呢,我们有C++的库了,因此我们就可以直接使用C++的库来完成这件事。
class MyQueue {
public:MyQueue() {}void push(int x) {_push.push(x);}int pop() {if(_pop.empty()){while(!_push.empty()){int val=_push.top();_push.pop();_pop.push(val);}}int val=_pop.top();_pop.pop();return val;}int peek() {if(_pop.empty()){while(!_push.empty()){int val=_push.top();_push.pop();_pop.push(val);}}return _pop.top();}bool empty() {return (_push.empty()&&_pop.empty());}
private:stack<int> _push;stack<int> _pop;
};/*** Your MyQueue object will be instantiated and called as such:* MyQueue* obj = new MyQueue();* obj->push(x);* int param_2 = obj->pop();* int param_3 = obj->peek();* bool param_4 = obj->empty();*/
5.用两个队列实现栈
题目链接:用两个队列实现栈
这道题与上面的题类似,我们也是曾经使用C语言做过,不过由于C语言没有轮子,就需要我们自己造轮子,有了很多的麻烦。
class MyStack {
public:MyStack() {}void push(int x) {if(q1.empty()){q2.push(x);}else{q1.push(x);}}int pop() {if(q1.empty()){while(q2.size()>1){int val=q2.front();q2.pop();q1.push(val);}int val=q2.front();q2.pop();return val;}else{while(q1.size()>1){int val=q1.front();q1.pop();q2.push(val);}int val=q1.front();q1.pop();return val;}}int top() {if(q1.empty()){return q2.back();}else{return q1.back();}}bool empty() {return (q1.empty()&&q2.empty());}
private:queue<int> q1;queue<int> q2;
};/*** Your MyStack object will be instantiated and called as such:* MyStack* obj = new MyStack();* obj->push(x);* int param_2 = obj->pop();* int param_3 = obj->top();* bool param_4 = obj->empty();*/
6.二叉树的层序遍历
题目链接:二叉树的层序遍历
对于这道题,如果不是用C++来完成的话,用C去完成的话是非常难的。不仅我们要确保我们造的轮子是正确的,而且还有很多细节需要进行处理,但我们如果使用C++的话可以极大的简化很多操作
1.双队列
我们可以使用两个队列去完成这件事,一个队列用来存储结点指针,一个队列用来存储该节点处于哪个层。这样我们就可以知道哪个结点是那个层的了,自然我们就很容易的得知层序遍历了。
2.用一个变量levelSize去控制
这种思路是比较奇妙的,我们使用一个变量来确定当前该层有多少个结点,用一个队列来存储结点,然后就是层序遍历的基本套路,每出一个结点,带来两个孩子。将每一层的数据存储在一个vector中,然后一层结束后将这一层的vector插入到vector<vector<int>>中。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> q;int levelSize=0;if(root){q.push(root);levelSize=1;}vector<vector<int>> vv;while(!q.empty()){vector<int> v;for(int i=0;i<levelSize;i++){TreeNode* front=q.front();q.pop();v.push_back(front->val);if(front->left){q.push(front->left);}if(front->right){q.push(front->right);}}vv.push_back(v);levelSize=q.size();}return vv;}
};
7.二叉树的层序遍历Ⅱ
题目链接:二叉树的层序遍历Ⅱ
对于这道题目,我们可以注意到他是让倒着遍历的。和前一道题基本是一样的,只是改变了vv的顺序。即相当于将vv给逆序。那么这道题就太简单了,直接将前面这道题给拷贝过来,然后调用库里面的reverse即可
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {queue<TreeNode*> q;int levelSize=0;if(root){q.push(root);levelSize=1;}vector<vector<int>> vv;while(!q.empty()){vector<int> v;for(int i=0;i<levelSize;i++){TreeNode* front=q.front();q.pop();v.push_back(front->val);if(front->left){q.push(front->left);}if(front->right){q.push(front->right);}}vv.push_back(v);levelSize=q.size();}reverse(vv.begin(),vv.end());return vv;}
};
好了,本期内容就到这里了
如果对你有帮助的话,不要忘记点赞加收藏哦!!!
相关文章:

【C++从0到王者】第十六站:stack和queue的使用
文章目录 一、stack的使用1.stack的介绍2.stack的使用 二、queue的使用1.queue的护额晒2.queue的使用 三、stack和queue相关算法题1.最小栈2.栈的压入、弹出序列3.逆波兰表达式4.两个栈实现一个队列5.用两个队列实现栈6.二叉树的层序遍历1.双队列2.用一个变量levelSize去控制 7…...

centos7 部署Tomcat和jpress应用
目录 一、静态、动态、伪静态 二、Web 1.0 和 Web 2.0 三、centos7 部署Tomcat 3.1 安装、配置jdk 3.2 安装 Tomcat 3.3 配置服务启动脚本 3.3.1 创建用户和组 3.3.2 创建tomcat.conf文件 3.3.3 创建服务脚本(tomcat.service) 3.3.4 重新加载守护进程并且测试 四、部…...

Unity Shader:常用的C#与shader交互的方法
俗话说久病成医,虽然不是专业技术美术,但代码写久了自然会积累一些常用的shader交互方法。零零散散的,总结如下: 1,改变UGUI的材质球属性 有时候我们需要改变ui的一些属性,从而实现想要的效果。通常UGUI上…...

luajit 使用 clang编译的坑
为了尝试将LuaJIT接入虚幻Lua插件之中,需要预编译LuaJIT链接库,在桌面平台问题不大, 主要是移动平台,涉及跨平台编译,因为对跨平台编译具体细节没有系统研究,这里先记录一下跨平台编译LuaJIT的主要过程 由于官方提供的…...

[SWPUCTF 2021 新生赛]Do_you_know_http
打开环境,根据题目提示,应该是考察http相关的东西 打开环境提示说请使用wLLm浏览器访问 那我们更改浏览器信息,在burp重发器中发包后发现是302重定向,但是提示说success成功,说明 我们修改是成功的,既然是…...

web前端之CSS
文章目录 一、CSS简介1.1 CSS语法规则 二、CSS的引用方法2.1 定义行内样式表2.2定义内部样式表2.3链入外部样式表2.4导入外部样式表 三、CSS选择符3.1 基本选择符3.1.1 标签选择符3.1.2 class类选择符3.1.3 id选择符 3.2 复合选择符3.2.1 交集选择符(合并选择器&…...

HarmonyOS元服务开发实践:桌面卡片字典
一、项目说明 1.DEMO创意为卡片字典。 2.不同卡片显示不同内容:微卡、小卡、中卡、大卡,根据不同卡片特征显示同一个字的不同内容,基于用户习惯可选择喜欢的卡片。 3.万能卡片刷新:用户点击卡片刷新按钮查看新内容,同时…...
xLua学习
xLua教程:https://github.com/Tencent/xLua/blob/master/Assets/XLua/Doc/XLua%E6%95%99%E7%A8%8B.md xLua配置:https://github.com/Tencent/xLua/blob/master/Assets/XLua/Doc/configure.md FAQ:https://github.com/Tencent/xLua/blob/maste…...

Web3到底是个啥?
Web3到底是个啥? Web3是近两年来科技领域最火热的概念之一,但是目前对于Web3的定义却仍然没有形成标准答案,相当多对于Web3的理解,都是建立在虚拟货币行业(即俗称的“币圈”)的逻辑基础之上的。 区块链服务…...
pycharm、idea、golang等JetBrains其他IDE修改行分隔符(换行符)
文章目录 pycharm、idea、golang系列修改行分隔符我应该选择什么换行符JetBrains IDE,默认行分隔符 是跟随系统修改JetBrains IDE,默认行分隔符 pycharm、idea、golang系列修改行分隔符 一般来说,不同的开发环境和项目对换行格式的使用偏好不同: Windo…...

ThinkPHP函数深度解析
ThinkPHP是一个具有丰富功能和强大灵活性的PHP开发框架。在这篇文章中,我们将详细介绍ThinkPHP的一些关键函数,以帮助开发人员更好地理解和使用这个框架。 1. 入门:ThinkPHP的核心函数 1.1 C()函数 C()函数用于读取和设置配置参数。它是Thin…...
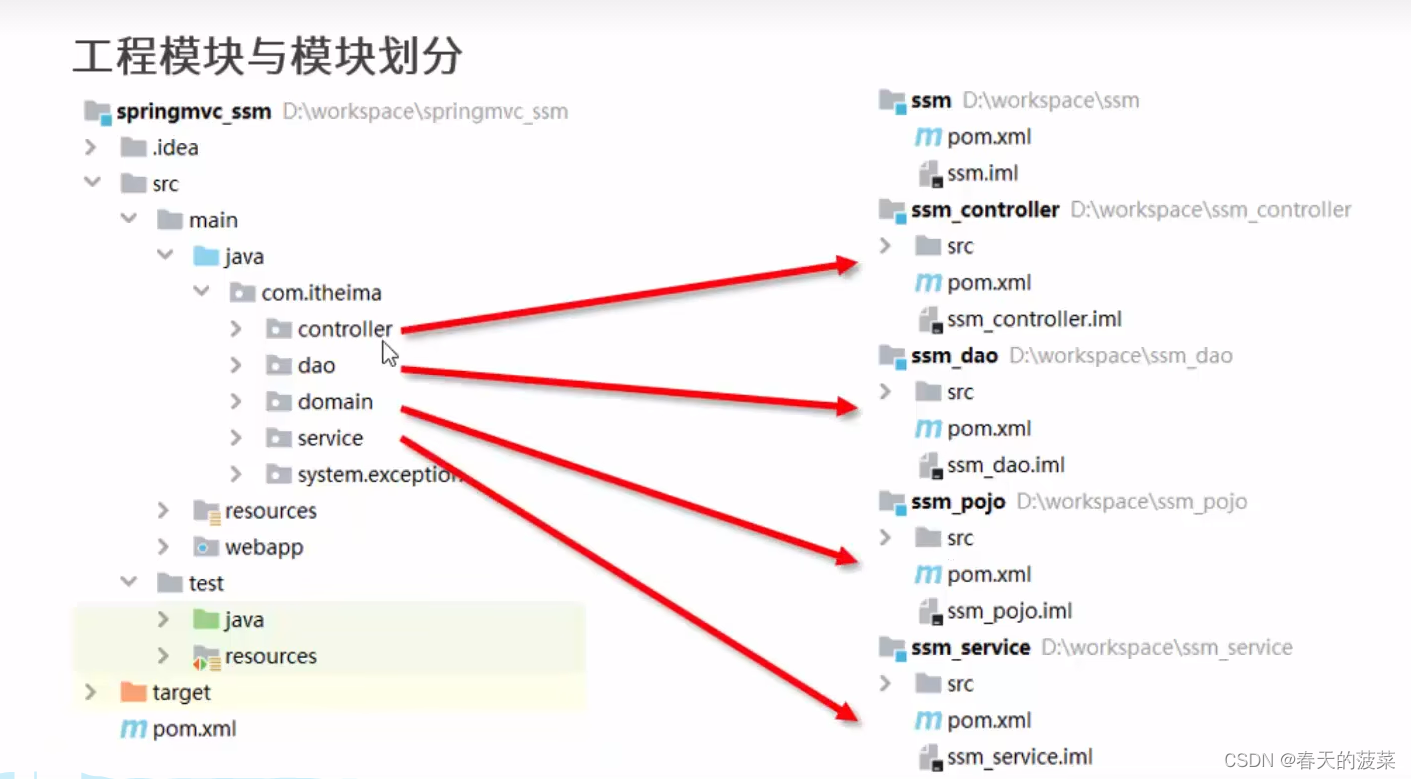
【java】【maven】【高级】MAVEN聚合继承属性等
目录 1、模块开发与设计 2、聚合 2、继承 3、属性 4、版本管理 5、资源配置 6、多环境配置 7、多环境开发配置 8、跳过测试 9、私服 前言:maven的高级使用包含分模块开发与设计、聚合、继承、属性、版本管理、资源配置、多环境配置、多环境开发配置、跳过…...
LeetCode150道面试经典题-合并两个有序数组(简单)
合并两个有序数组 题目: 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意&a…...

记录 运维三剑客一件部署的的docker-compose,yml文件
CAdvisor: 收集 InfluxDB: 存储 Grafana: 展示 version: 3.1volumes:grafana_data: {}services:influxdb:image: tutum/influxdb:0.9restart: alwaysenvironment:- PRE_CREATE_DBcadvisorports:- "8083:8083"- "8086:8086"volumes:- ./data/inf…...
Xposed框架开发
文章目录 xpose插件开发步骤清单文件新建一个类(插件入口点)设置入口点 Hook第一个实例zhuceji.apk一些常用的HOOKHookH5PluginHookProxyPluginHookSystem 资料Xposed原理初探 xpose插件开发步骤 magisk安装与配置 Xpose Framework API LSPosed magisk …...
)
2.13 Android ebpf非网络相关帮助函数API汇总(十二 本章完)
1.long bpf_user_ringbuf_drain(struct bpf_map *map, void *callback_fn, void *ctx, u64 flags) 描述:从指定的用户环形缓冲区中排出样本,并为每个此类样本调用提供的回调: long (*callback_fn)(struct bpf_dynptr *dynptr, void *ctx); 如果callback_fn返回0,帮助函数…...
关于游戏的笔记
关于搭建秦时明月2一键端,并且开启秘境神秘商人东海寻仙幻化 1.该游戏下主要的目录 gm端 服务框架 服务端 2.修改对应的文件 C:\qs\Q2Server\server\conf_common\ManagerAddress.xmlC:\qs\Q2Server\server\conf_manager\GateServer.xml修改ip 3.启动gm startup…...
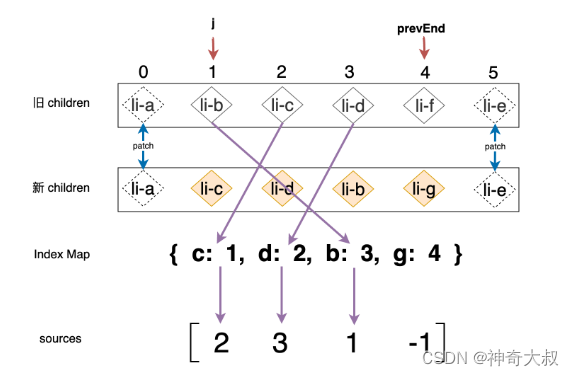
vue diff 前后缀+最长递增子序列算法
文章目录 查找相同前后缀通过前后缀位置信息新增节点通过前后缀位置信息删除节点 中间部份 diff判断节点是否需要移动删除节点删除未查找到的节点删除多余节点 移动和新增节点最长递增子序列 求解最长递增子序列位置信息 查找相同前后缀 如上图所示,新旧 children 拥…...

【Python】Locust持续优化:InfluxDB与Grafana实现数据持久化与可视化分析
目录 前言 influxDB 安装运行InfluxDB 用Python 上报数据到influxdb ocust 数据写入到 influx Locust的生命周期 上报数据 优化升级 配置Grafana 总结 资料获取方法 前言 在进行性能测试时,我们需要对测试结果进行监控和分析,以便于及时发现问…...

数组模拟循环链表
5073. 空闲块 - AcWing题库 数组模拟循环链表 /*从当前位置开始遍历空闲块链表(初始是从地址最小的第一个空闲块开始),寻找满足条件的最小块 (即:大于等于请求空间的最小空闲块,如果有多个大小相同的最小空…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
