机器学习基础算法及其实现
线性回归
知识点:
1. 线性回归模型可以使用不同的目标函数,最常用的是最小二乘法、最小绝对值法和最大似然法。
2. 在最小二乘法中,目标是最小化实际值与预测值之间的误差平方和,这可以通过求导数等方法来求解。
3. 在最小绝对值法中,目标是最小化实际值与预测值之间的误差绝对值和,这可以使用线性规划等方法来求解。
4. 在最大似然法中,目标是估计模型参数,使得在给定自变量的条件下,因变量的概率最大化。
5. 线性回归模型的参数估计可以使用基于梯度下降的算法,如批量梯度下降、随机梯度下降、小批量梯度下降等。
6. 在应用线性回归模型时,需要注意多重共线性、异方差性、自相关等问题,并采取相应的处理措施。
7. 除了传统的线性回归模型,还有多项式回归、岭回归、lasso回归、弹性网络回归等变种模型。
逻辑回归
import numpy as npclass LogisticRegression:def __init__(self, learning_rate=0.01, num_iterations=10):self.learning_rate = learning_rateself.num_iterations = num_iterationsself.weights = Noneself.bias = Nonedef fit(self, X, y):num_samples, num_features = X.shapeprint(num_samples,num_features)self.weights = np.zeros(num_features)print(X)print(self.weights)self.bias = 0# 梯度下降算法for i in range(self.num_iterations):linear_model = np.dot(X, self.weights) + self.biasprint(linear_model)y_pred = self._sigmoid(linear_model)print("sigmoid")print(y_pred)print("end")# 计算损失函数的梯度dw = (1 / num_samples) * np.dot(X.T, (y_pred - y))db = (1 / num_samples) * np.sum(y_pred - y)# 更新权重和偏移量self.weights -= self.learning_rate * dwself.bias -= self.learning_rate * dbdef predict(self, X):print("pre")print(X)linear_model = np.dot(X, self.weights) + self.biasy_pred = self._sigmoid(linear_model)y_pred_class = [1 if i > 0.5 else 0 for i in y_pred]return np.array(y_pred_class)def _sigmoid(self, x):return 1 / (1 + np.exp(-x))# 创建训练数据
X_train = np.array([[1,2,3],[2,3,4],[3,4,5],[4,5,6], [5,6,7]])
y_train = np.array([0, 0, 1, 1, 1])# 创建逻辑回归模型
lr_model = LogisticRegression()# 训练模型
lr_model.fit(X_train, y_train)# 预测新数据
X_new = np.array([[2,4,6], [3,5,7]])
y_pred = lr_model.predict(X_new)print(y_pred)
SVM
基于sklearn库实现SVM:
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score# 加载数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建 SVM 模型对象
svm_model = SVC(kernel='linear', C=1)# 训练 SVM 模型
svm_model.fit(X_train, y_train)# 预测测试集数据
y_pred = svm_model.predict(X_test)# 计算准确率
acc = accuracy_score(y_test, y_pred)
print('Accuracy:', acc)
具体代码实现:(复习后再过来研究)
import numpy as np# 定义 SVM 模型类
class SVM:def __init__(self, C=1.0, kernel='linear', gamma=1.0):self.C = C # 惩罚系数self.kernel = kernel # 核函数类型self.gamma = gamma # 核函数参数self.alpha = None # 拉格朗日乘子self.b = 0 # 阈值self.X = None # 训练数据self.y = None # 训练标签# 核函数def _kernel_function(self, x1, x2):if self.kernel == 'linear':return np.dot(x1, x2)elif self.kernel == 'rbf':return np.exp(-self.gamma * np.linalg.norm(x1 - x2) ** 2)else:raise ValueError('Unsupported kernel function type')# 训练模型def fit(self, X, y):n_samples, n_features = X.shape # 5 3 self.alpha = np.zeros(n_samples)self.X = Xself.y = y# 计算 Gram 矩阵K = np.zeros((n_samples, n_samples)) # 5 5for i in range(n_samples):for j in range(n_samples):K[i, j] = self._kernel_function(X[i], X[j]) # np.dot# 定义优化目标函数def objective_function(alpha):return 0.5 * np.dot(alpha, np.dot(alpha, K)) - np.sum(alpha)# 定义约束条件def zero_sum_constraint(alpha):return np.dot(alpha, y)# 定义不等式约束条件bounds = [(0, self.C) for i in range(n_samples)]cons = [{'type': 'eq', 'fun': zero_sum_constraint}]# 使用优化算法求解拉格朗日乘子from scipy.optimize import minimizeres = minimize(objective_function, self.alpha, bounds=bounds, constraints=cons)self.alpha = res.x# 计算阈值support_vectors = self.alpha > 1e-5support_vectors_idx = np.where(support_vectors)[0]self.b = np.mean(y[support_vectors] - np.dot(K[support_vectors_idx, :], self.alpha * y))# 预测新数据def predict(self, X):n_samples = X.shape[0]y_pred = np.zeros(n_samples)for i in range(n_samples):s = 0for alpha, x, y in zip(self.alpha, self.X, self.y):s += alpha * y * self._kernel_function(X[i], x)y_pred[i] = s + self.breturn np.sign(y_pred)# 创建训练数据
X_train = np.array([[1,2,3],[2,3,4],[3,4,5],[4,5,6], [5,6,7]])
y_train = np.array([0, 0, 1, 1, 1])# 创建逻辑回归模型
model = SVM()# 训练模型
model.fit(X_train, y_train)# 预测新数据
X_new = np.array([[2,4,6], [3,5,7]])
y_pred = model.predict(X_new)print(y_pred)
相关文章:

机器学习基础算法及其实现
线性回归 知识点: 1. 线性回归模型可以使用不同的目标函数,最常用的是最小二乘法、最小绝对值法和最大似然法。 2. 在最小二乘法中,目标是最小化实际值与预测值之间的误差平方和,这可以通过求导数等方法来求解。 3. 在最小绝对值…...

docker安装MinIO
简介 Minio 是一个面向对象的简单高性能存储服务。使用 Go 语言编写,性能高、具有跨平台性。 Minio 官网为:https://min.io ,有一个中文站点,单内容更新不是很及时,建议从原始官网学习。 本文采用 Docker 安装&…...
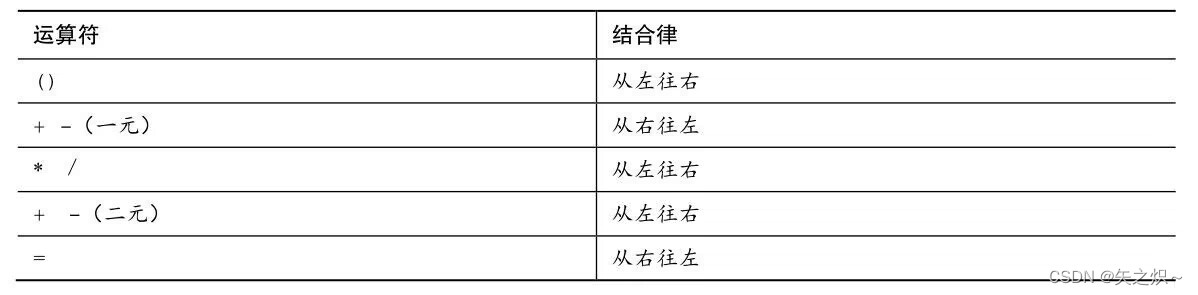
第5章 运算符、表达式和语句
本章介绍以下内容: 关键字:while、typedef 运算符:、-、*、/、%、、--、(类型名) C语言的各种运算符,包括用于普通数学运算的运算符 运算符优先级以及语句、表达式的含义 while循环 复合语句、自动类型转换和强制类型转换 如何编写…...

24考研数据结构-图的存储结构邻接矩阵
目录 6.3 储存结构(邻接表表示法)1. 储存方式2. 结构3. 图的邻接表存储表示(算法)4. 结论5. 邻接矩阵和邻接表的对比邻接矩阵优点:缺点: 邻接表优点:缺点: 邻接矩阵与邻接表的关系 6…...
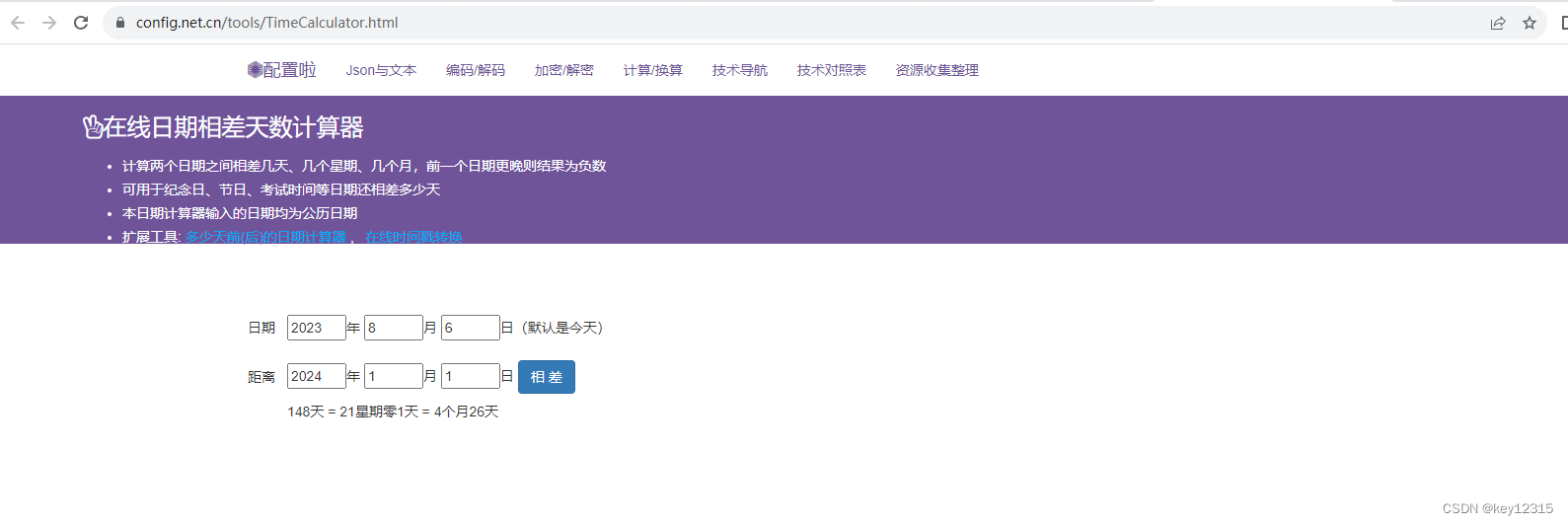
在线推算两个日期相差天数的计算器
具体请前往:在线推算两个日期相差天数的计算器...
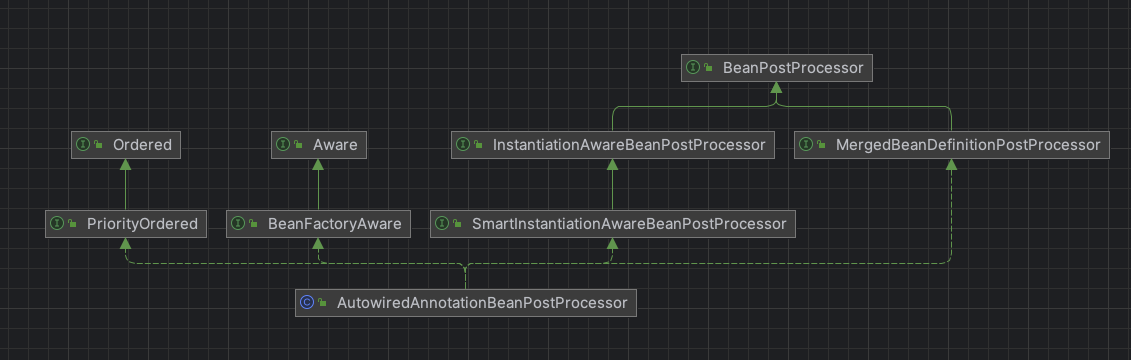
Spring源码解析(七):bean后置处理器AutowiredAnnotationBeanPostProcessor
Spring源码系列文章 Spring源码解析(一):环境搭建 Spring源码解析(二):bean容器的创建、默认后置处理器、扫描包路径bean Spring源码解析(三):bean容器的刷新 Spring源码解析(四):单例bean的创建流程 Spring源码解析(五)&…...

【C#学习笔记】引用类型(1)
文章目录 引用类型class匿名类 记录引用相等和值相等record声明 接口delegate 委托合并委托/多路广播委托 引用类型 引用类型的变量存储对其数据(对象)的引用,而值类型的变量直接包含其数据。 对于引用类型,两种变量可引用同一对…...
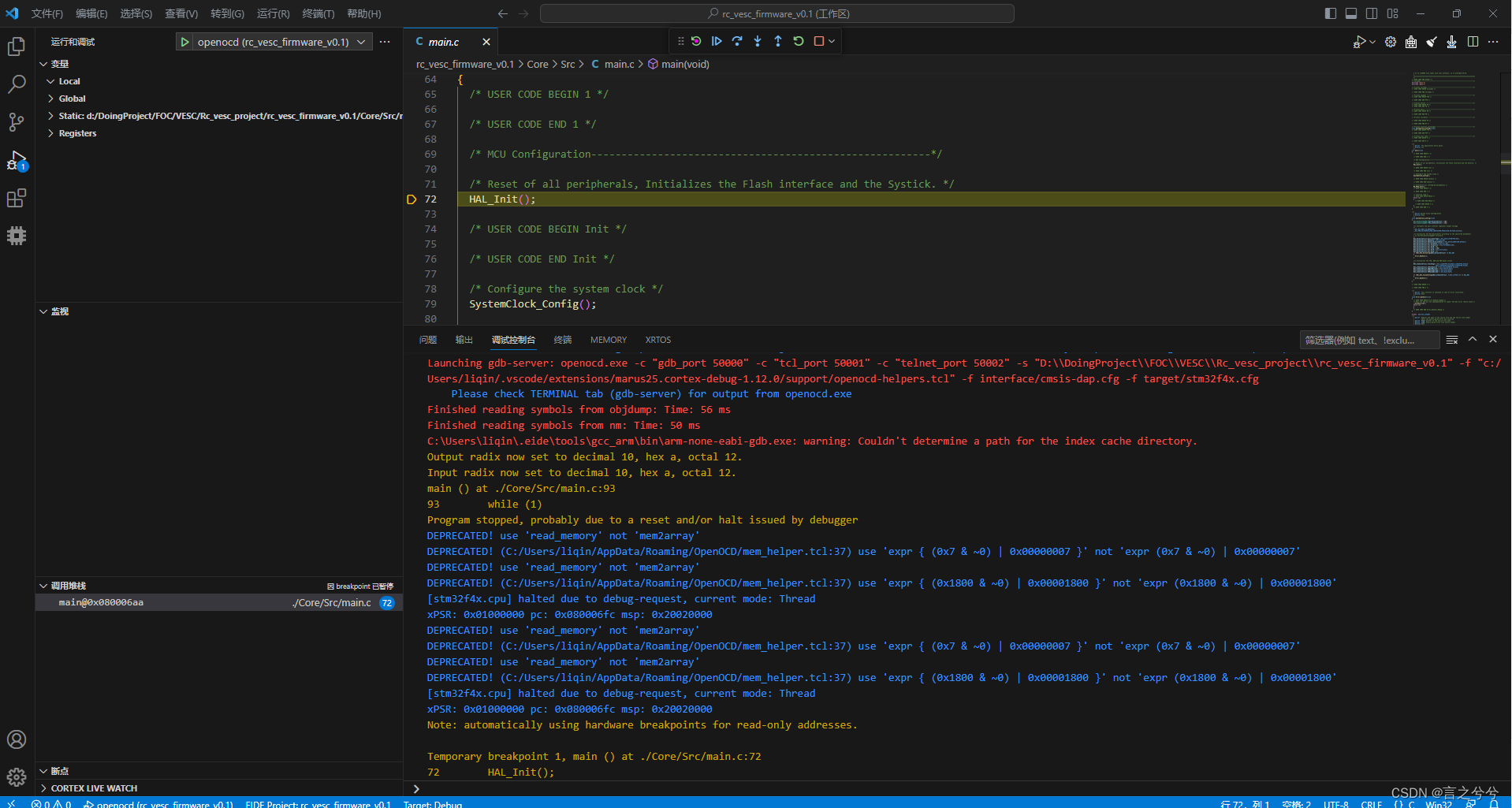
STM32CubeMX+VSCODE+EIDE+RT-THREAD 工程创建
Eide环境搭建暂且不表,后续补充。主要记录下Vscode环境下 创建Rt-thread工程的过程。分别介绍STM32CubeMX添加rtt支持包的方式和手动添加rtt kernel方式。STM32CubeMX生成工程的时候有"坑",防止下次忘记,方便渡一下有缘人ÿ…...

java中javamail发送带附件的邮件实现方法
java中javamail发送带附件的邮件实现方法 本文实例讲述了java中javamail发送带附件的邮件实现方法。分享给大家供大家参考。具体分析如下: JavaMail,顾名思义,提供给开发者处理电子邮件相关的编程接口。它是Sun发布的用来处理email的API。它…...
-稳定扩散百态:解密AI绘画工具「SD WebUI」的提示词高级使用策略)
Stable Diffusion高阶技能(2)-稳定扩散百态:解密AI绘画工具「SD WebUI」的提示词高级使用策略
简介 在我们的生活中,艺术元素可谓无处不在,而处于中心地位的绘画,无疑是携带着强烈的艺术魅力。现如今随着AI技术的日新月异,AI绘画对我们的生活世界的改造影响越来越深远。那么,如何让我们在AI绘画工具中更好的指导AI完成我们心中的作品呢? 这需要我们玩转这个工具的…...

【果树农药喷洒机器人】Part2:机器人变量喷药系统硬件选型
本专栏介绍:付费专栏,持续更新机器人实战项目,欢迎各位订阅关注。 关注我,带你了解更多关于机器人、嵌入式、人工智能等方面的优质文章! 文章目录 一、引言二、变量喷药系统总体要求2.1系统功能要求2.2系统技术要求三、机器人关键硬件选型3.1深度相机概述与选型3.2单片机选…...
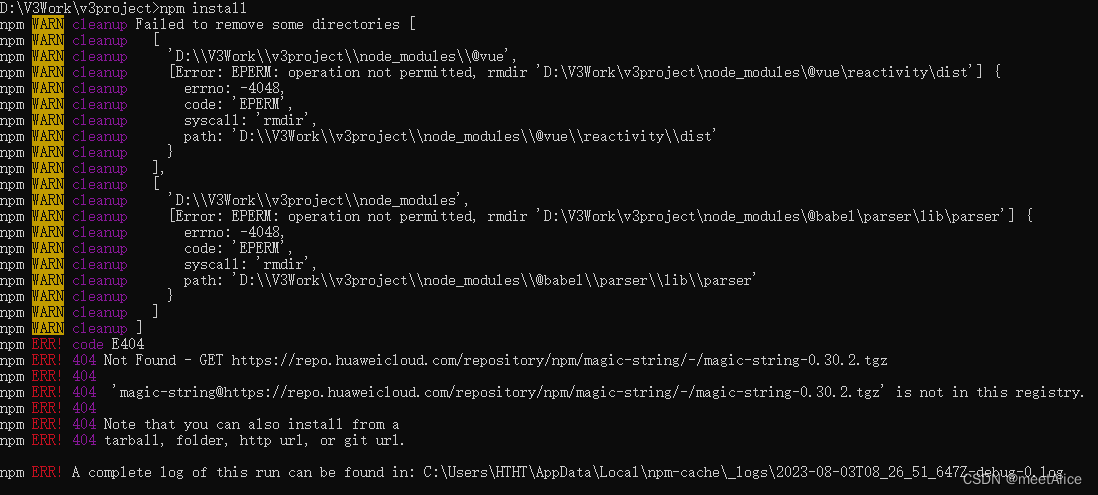
解决vite+vue3项目npm装包失败
报错如下: Failed to remove some directories [ npm WARN cleanup [ npm WARN cleanup D:\\V3Work\\v3project\\node_modules\\vue, npm WARN cleanup [Error: EPERM: operation not permitted, rmdir D:\V3Work\v3project\node_modules\vue\reactivity\…...

Rust之错误处理
在Rust中,将错误分为两种,可恢复错误和不可恢复错误。所谓可恢复错误就是指类似于文件未找到这类错误,一般需要将它们报告给用户并再次尝试进行操作,而不可恢复错误往往就是Bug,需要停止程序的运行。 1、不可恢复错误…...

docker compose快速编排
Docker-compose概述 Docker-Compose项目是Docker官方的开源项目,负责实现对Docker容集群的快速编排 Docker-Compose将所管理的容器分为三层,分别是工程(project),服务(service)以及容器&#x…...

java.io.File类的使用
文章目录 概述构造器常用方法1、获取文件和目录基本信息2、列出目录的下一级3.File类的重命名功能4、判断功能的方法5、创建、删除功能 练习 概述 File类及本章下的各种流,都定义在java.io包下。一个File对象代表硬盘或网络中可能存在的一个文件或者文件目录&#…...
)
TypeScript技能总结(三)
typescript是js的超集,目前很多前端框架都开始使用它来作为项目的维护管理的工具,还在不断地更新,添加新功能中,我们学习它,才能更好的在的项目中运用它,发挥它的最大功效 //泛型 > 参数和返回值类型相…...
python绿色版运行程序,python 绿色版免安装
大家好,小编来为大家解答以下问题,python绿色版运行程序,python 绿色版免安装,今天让我们一起来看看吧! 软件简介 Python3.7.0 是一种被广大从业者广泛使用的通用型设计语言。该软件提供了丰富全面的模块,并…...

Python 向Excel写数据
1.项目终端导入 xlwt 库 pip install xlwt2.导入依赖包 import xlwt3.创建Excel表格类型文件 调用xlwt模块中的Workbook方法来创建一个excel表格类型文件,其中的第一个参数是设置数据的编码格式,这里是’utf-8’的形式,style_compression设…...
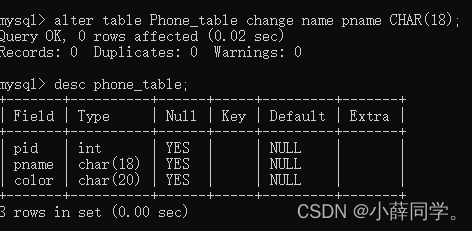
MySQL(1)
MySQL创建数据库和创建数据表 创建数据库 1. 连接 MySQL mysql -u root -p 2. 查看当前的数据库 show databases; 3. 创建数据库 create database 数据库名; 创建数据库 4. 创建数据库时设置字符编码 create database 数据库名 character set utf8; 5. 查看和显示…...
增加OTG升级功能)
Android10 Recovery系列(二)增加OTG升级功能
一 、背景 起因是遇到了客户有这个需求,本着了解的原则,去看了一下之前Android版本的代码,想看看之前有没有现成的实现,移植过来。结果很不幸,没有找到。于是自己开始了功能实现的过程。下面分享一下该功能的实现 二 、准备工作 首先简单了解一下Recovery 模块的系统升…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...
