数据结构 | 搜索和排序——排序
目录
一、冒泡排序
二、选择排序
三、插入排序
四、希尔排序
五、归并排序
六、快速排序
排序是指将集合中的元素按照某种顺序排序的过程。
一、冒泡排序
冒泡排序多次遍历列表。它比较相邻的元素,将不合顺序的交换。每一轮遍历都将下一个最大值放到正确的位置上。本质上,每个元素通过“冒泡”找到自己所属的位置。
冒泡排序需要遍历的轮数是n-1,完成n-1轮后,最小的元素必然在正确的位置上,因此不必再做处理。
冒泡排序函数bubbleSort:
def bubbleSort(alist):for passnum in range(len(alist)-1,0,-1):for i in range(passnum):if alist[i]>alist[i+1]:temp=alist[i]alist[i]=alist[i+1]alist[i+1]=tempPython允许同时赋值,执行语句a,b=b,a,相当于同时执行两条赋值语句。
冒泡排序算法中,给含有n个元素的列表排序总需要遍历n-1轮,总的比较次数是前n-1个整数之和,因此前n-1个整数之和就是。这表明,该算法的时间复杂度是
。在最好的情况下,列表是已经有序的,不需要执行交换操作。在最坏情况下,每一次比较都将导致一次交换。
冒泡排序通常被认为是效率最低的排序算法,因为在确定最终的位置前必须交换元素。“多余”的交换操作代价很大。不过,由于冒泡排序要遍历列表中未排序的部分,因此它具有其他排序算法没有的用途。特别是,如果在一轮遍历中没有发生元素交换,就可以确定列表已经有序。可以修改冒泡排序函数,使其在遇到这种情况时提前终止。对于只需要遍历几次的列表,冒泡排序可能有优势,因此它能判断出有序列表并终止排序过程。这种排序通常被称为短冒泡。
修改后的冒泡排序函数:
def shortBubbleSort(alist):exchanges=Truepassnum=len(alist)-1while passnum>0 and exchanges:exchanges=Falsefor i in range(passnum):if alist[i]>alist[i+1]:exchanges=Truetemp=alist[i]alist[i]=alist[i+1]alist[i+1]=temppassnum=passnum-1二、选择排序
选择排序在冒泡排序的基础上做了改进,每次遍历列表时只做一次交换。要实现这一点,选择排序在每次遍历时寻找最大值,并在遍历完之后将它放到正确位置上。和冒泡排序一样,第一次遍历后,最大的元素就位;第二次遍历后,第二大的元素就位,依此类推。若给n个元素排序,需要遍历n-1轮。
选择排序函数selectionSort:
def selectionSort(alist):for fillslot in range(len(alist)-1,0,-1):positionOfMax=0for location in range(1,fillslot+1):if alist[location]>alist[positionOfMax]:positionOfMax=locationtemp=alist[fillslot]alist[fillslot]=alist[positionOfMax]alist[positionOfMax]=temp可以看出,选择排序算法和冒泡排序算法的比较次数相同,所以时间复杂度也是。但是,由于减少了交换次数,因此选择排序算法通常更快。
三、插入排序
插入排序的时间复杂度也是,但原理稍有不同。它在列表较低的一端维护一个有序的子列表,并逐个将每个新元素“插入”这个子列表。
首先假设位置0处的元素是只含单个元素的有序子列表。从元素1到元素n-1,每一轮都将当前元素与有序子列表中的元素进行比较。在有序子列表中,将比它大的元素右移;当遇到一个比他小的元素或抵达子列表终点时,就可以插入当前元素。
在给n个元素排序时,插入排序算法需要遍历n-1轮。循环从位置1开始,直到位置n-1结束,这些元素都需要被插入到有序子列表中。
插入排序函数insertionSort:
def insertionSort(alist):for index in range(1,len(alist)):currentvalue=alist[index]position=indexwhile position>0 and alist[position-1]>currentvalue:alist[position]=alist[position-1]position=position-1alist[position]=currentvalue 在最坏的情况下,插入排序算法的比较次数是前n-1个整数之和,对应的时间复杂度是。在最好的情况下(列表已经是有序的),每一轮只需比较一次。
移动操作和交换操作有一个重要的不同点。总体来说,交换操作的处理时间大约是移动操作的3倍,因为后者只需进行一次赋值。在基准测试中,插入排序算法的性能很不错。
四、希尔排序
希尔排序也称“递减增量排序”,它对插入排序做了改进,将列表分成数个子列表,并对每一个列表应用插入排序。如何切分列表是希尔排序的关键——并不是连续切分,而是使用增量i(有时称作步长)选取所有间隔为i的元素组成子列表。
希尔排序函数shellSort:
def shellSort(alist):sublistcount=len(alist)//2while sublistcount>0:for startposition in range(sublistcount):gapInsertionSort(alist,startposition,sublistcount)print("After increments of size",sublistcount,"The list is",alist)sublistcount=sublistcount//2def gapInsertionSort(alist,start,gap):for i in range(start+gap,len(alist),gap):currentvalue=alist[i]position=iwhile position>=gap and alist[position-gap]>currentvalue:alist[position]=alist[position-gap]position=position-gapalist[position]=currentvalueif __name__=="__main__":alist=[54,26,93,17,77,31,44,55,20]print(shellSort(alist))
希尔排序的时间复杂度大概介于和
之间。希尔排序的时间复杂度可以达到
。
五、归并排序
归并排序是递归算法,使用了分治策略,每次将一个列表一分为二,如果列表为空或只有一个元素,那么从定义上来说它就是有序的(基本情况)。如果列表不止一个元素,就将列表一分为二,并对两部分都递归调用并归并排序。当两部分都有序后,就进行归并这一基本操作。归并是指将两个较小的有序列表归并为一个有序列表的过程。
归并排序函数mergeSort:
def mergeSort(alist):print("Spiltting ",alist)if len(alist)>1:mid=len(alist)//2lefthalf=alist[:mid]rightleft=alist[mid:]mergeSort(lefthalf)mergeSort(rightleft)i=0j=0k=0while i<len(lefthalf) and j<len(rightleft):if lefthalf[i]<rightleft[j]:alist[k]=lefthalf[i]i=i+1else:alist[k]=rightleft[j]j=j+1k=k+1while i<len(lefthalf):alist[k]=lefthalf[i]i=i+1k=k+1while j<len(rightleft):alist[k]=rightleft[j]j=j+1k=k+1print("Merging ",alist)if __name__=="__main__":b=[54,26,93,17,77,31,44,55,20]print(mergeSort(b))运行结果如下:
Spiltting [54, 26, 93, 17, 77, 31, 44, 55, 20]
Spiltting [54, 26, 93, 17]
Spiltting [54, 26]
Spiltting [54]
Merging [54]
Spiltting [26]
Merging [26]
Merging [26, 54]
Spiltting [93, 17]
Spiltting [93]
Merging [93]
Spiltting [17]
Merging [17]
Merging [17, 93]
Merging [17, 26, 54, 93]
Spiltting [77, 31, 44, 55, 20]
Spiltting [77, 31]
Spiltting [77]
Merging [77]
Spiltting [31]
Merging [31]
Merging [31, 77]
Spiltting [44, 55, 20]
Spiltting [44]
Merging [44]
Spiltting [55, 20]
Spiltting [55]
Merging [55]
Spiltting [20]
Merging [20]
Merging [20, 55]
Merging [20, 44, 55]
Merging [20, 31, 44, 55, 77]
Merging [17, 20, 26, 31, 44, 54, 55, 77, 93]
None
归并操作每次从有序列表中取出最小值,放回初始列表。
归并排序算法的时间复杂度是。
六、快速排序
和归并排序一样,快速排序也采用分治策略,但不使用额外的存储空间。不过,代价是列表可能不会被一分为二。出现这种情况,算法的效率会有所下降。
快速排序算法首先选出一个基准值。基准值的作用是帮助切分列表。在最终的有序列表中,基准值的位置通常被称作分割点,算法在分割点切分列表,以继续对快速排序的子调用。
找到基准值后,下一步是分区操作。它会找到分割点,同时将其他元素放到正确的一边——要么大于基准值,要么小于基准值。
分区操作首先找到两个坐标——leftmark和rightmark——它们分别位于列表剩余元素的开头和结尾。分区的目的是根据排序元素与基准值的相对大小将它们放到正确的一边,同时逐渐逼近分割点。
首先加大leftmark,直到遇到一个大于基准值的元素。然后减小rightmark,直到遇到一个小于基准值的元素。这样一来,就找到两个与最终的分割点错序的元素。互换这两个元素,然后重复上述过程。
当rightmark小于leftmark时,过程终止。此时,rightmark的位置就是分割点。将基准值与当前位于分割点的元素互换,即可使基准值位于正确的位置。分割点左边的所有元素都小于基准值,右边的所有元素都大于基准值。因此,可以在分割点处将列表一分为二,并针对左右两部分递归调用快速排序函数。
快速排序函数quickSort:
def quickSort(alist):quickSortHelper(alist,0,len(alist)-1)def quickSortHelper(alist,first,last):if first<last:splitpoint=partition(alist,first,last)quickSortHelper(alist,first,splitpoint-1)quickSortHelper(alist,splitpoint+1,last)def partition(alist,first,last):pivotvalue=alist[first]leftmark=first+1rightmark=lastdone=Falsewhile not done:while leftmark<=rightmark and alist[leftmark]<=pivotvalue:leftmark=leftmark+1while alist[rightmark]>=pivotvalue and rightmark>=leftmark:rightmark=rightmark-1if rightmark<leftmark:done=Trueelse:temp=alist[leftmark]alist[leftmark]=alist[rightmark]alist[rightmark]=temptemp=alist[first]alist[first]=alist[rightmark]alist[rightmark]=tempreturn rightmark快速排序的时间复杂度是。另外,快速排序算法不需要像归并排序算法那样使用额外的存储空间。
相关文章:
数据结构 | 搜索和排序——排序
目录 一、冒泡排序 二、选择排序 三、插入排序 四、希尔排序 五、归并排序 六、快速排序 排序是指将集合中的元素按照某种顺序排序的过程。 一、冒泡排序 冒泡排序多次遍历列表。它比较相邻的元素,将不合顺序的交换。每一轮遍历都将下一个最大值放到正确的位…...

【嵌入式环境下linux内核及驱动学习笔记-(18)LCD驱动框架1-LCD控制原理】
目录 1、LCD显示系统介绍1.1 LCD显示基本原理1.1.1 颜色的显示原理:1.1.2 图像的构成 1.2 LCD接口介绍1.2.1 驱动接口 - MCU接口1.2.2 驱动接口 - RGB接口1.2.3 驱动接口 - LVDS接口1.2.4 驱动接口 - MIPI接口1.2.5 RGB / MIPI / LVDS三种接口方式的区别:…...
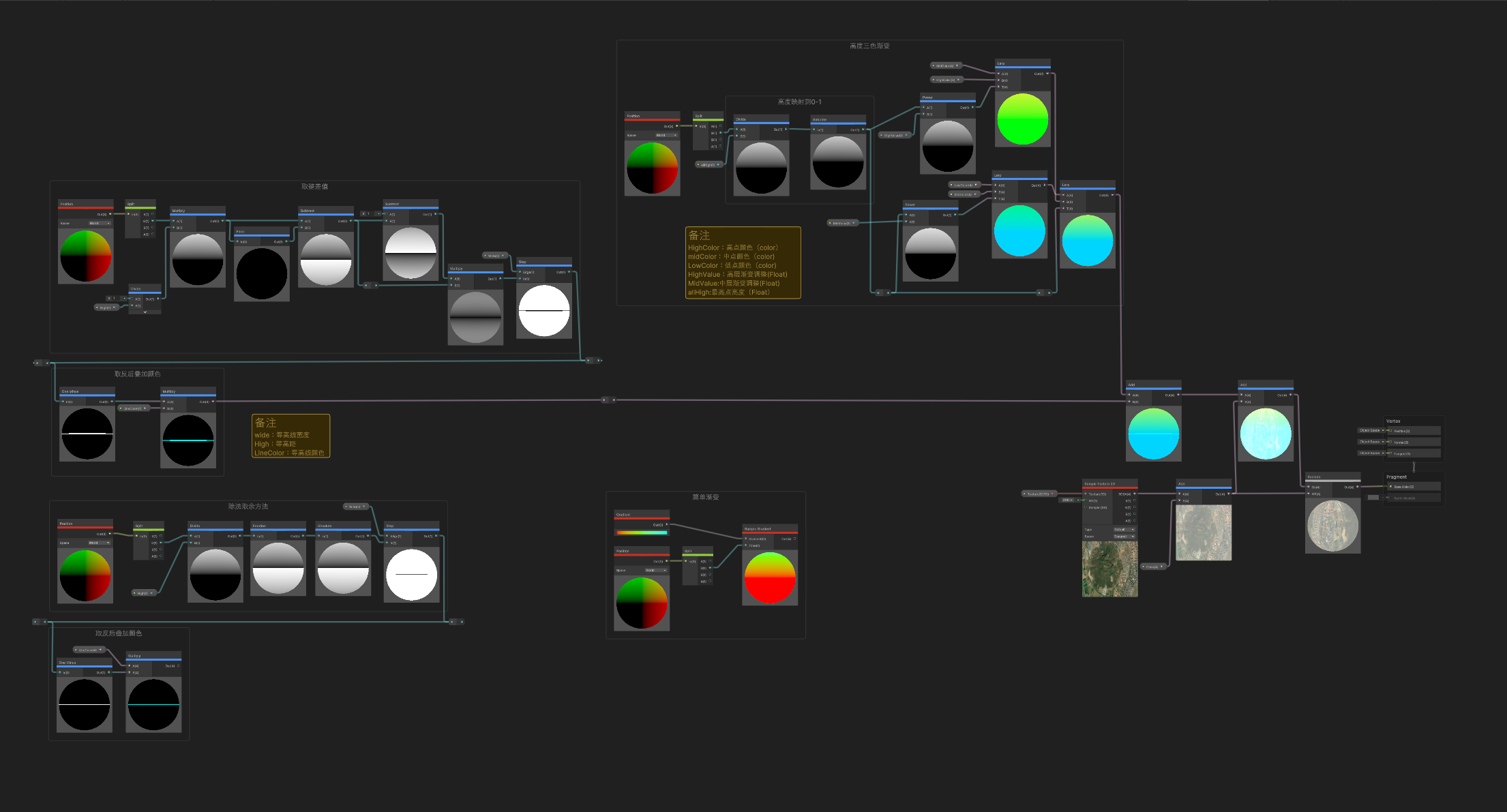
【unity】ShaderGraph实现等高线和高程渐变设色
【unity】ShaderGraph实现等高线和高程渐变设色 等高线的实现思路 方法一: 通过Position节点得到顶点的高度(y)值,将高度值除去等高距离取余,设定余数的输出边界(step) 方法二: 将…...
快速修复应用程序中的问题的利器—— Android热修复
热修复技术在Android开发中扮演着重要的角色,它可以帮助开发者在不需要重新发布应用程序的情况下修复已经上线的应用程序中的bug或者添加新的功能。 一、热修复是什么? 热修复(HotFix)是一种在运行时修复应用程序中的问题的技术…...

什么是全局代理,手机怎么设置全局代理
目录 什么是全局代理 全局代理的优缺点 优点 缺点 手机怎么设置全局代理 注意事项 总结 在计算机网络和信息安全中,全局代理是一种常用的技术手段,用于将网络流量通过代理服务器进行转发和处理。本文将介绍什么是全局代理,探讨全局代理…...

技术领先产品ASSAR300一一基于SAR成像的角雷达产品,助力自动泊车
作为自动驾驶应用场景中最先被推广和商业化落地的自动泊车功能,目前是在一些限定环境下实现了功能跑通。面对多种多样的复杂停车场场景,系统需要不断增强感知算法能力或寻求新的传感器技术,来提升对周围环境感知和对障碍物探测的精准度。 传…...

单元测试之 - Spring框架提供的单元/集成测试注解
Spring框架提供了很多注解来辅助完成单元测试和集成测试(备注:这里的集成测试指容器内部的集成测试,非系统间的集成测试),先看看Spring框架提供了哪些注解以及对应的作用。RunWith(SpringRunner.class) / ExtendWith(SpringExtension.class)&…...
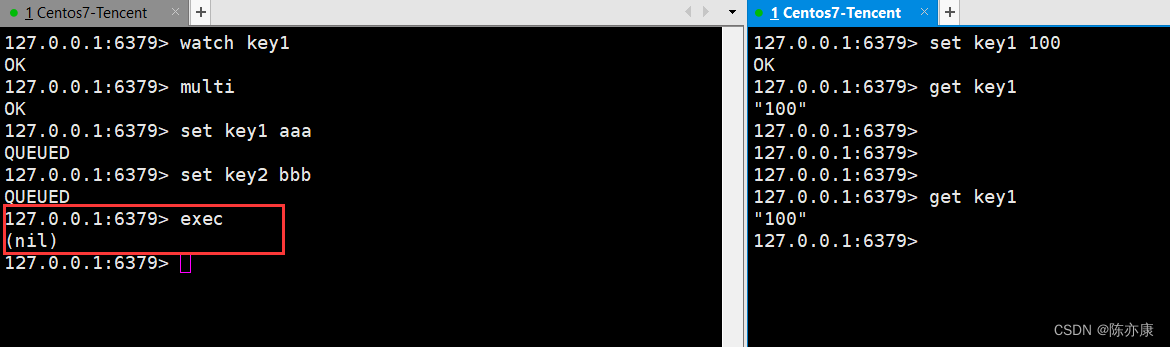
深入学习 Redis - 事务、实现原理、指令使用及场景
目录 一、Redis 事务 vs MySQL事务 二、Redis 事务的执行原理 2.1、执行原理 2.2、Redis 事务设计这么简单,为什么不涉及成 MySQL 那样强大呢? 三、Redis 事务的使用 3.1、使用场景 3.2、具体演示 开启/执行/放弃事务 watch 监控 watch 实现原理…...

异步javaScript
在本文中,我们将解释什么是异步编程,为什么我们需要它,并简要讨论 JavaScript 历史上异步函数是怎样被实现的。 预备知识:基本的计算机素养,以及对 JavaScript 基础知识的一定了解,包括函数和事件处理程序…...

看跨境电商世界区域分布,Live Market教你深入参与跨境创业
随着全球化发展带来互联网技术的进步和平台经济的触角伸向全球,跨境电商越来越成为全球贸易的重要组成部分。根据国际数据公司(IDC)的最新数据显示,全球前五大跨境电商平台分别是亚马逊、阿里巴巴、eBay、Wish和京东全球购。这五家…...
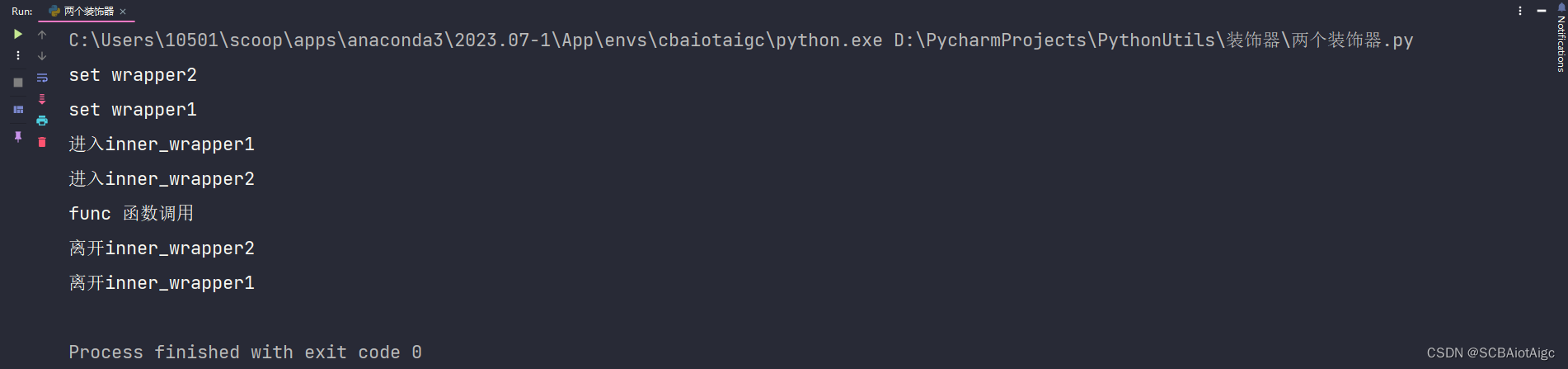
python中的装饰器的真正含义和用法
闭包: 闭包是python中的一个很实用的写法,可以使得用户在函数中调用该函数外的函数的变量,使得该变量常驻于内存中。 闭包函数: 输入是函数,输出也是一个函数。 装饰器的写法是python闭包的语法糖。 面试中经常面…...
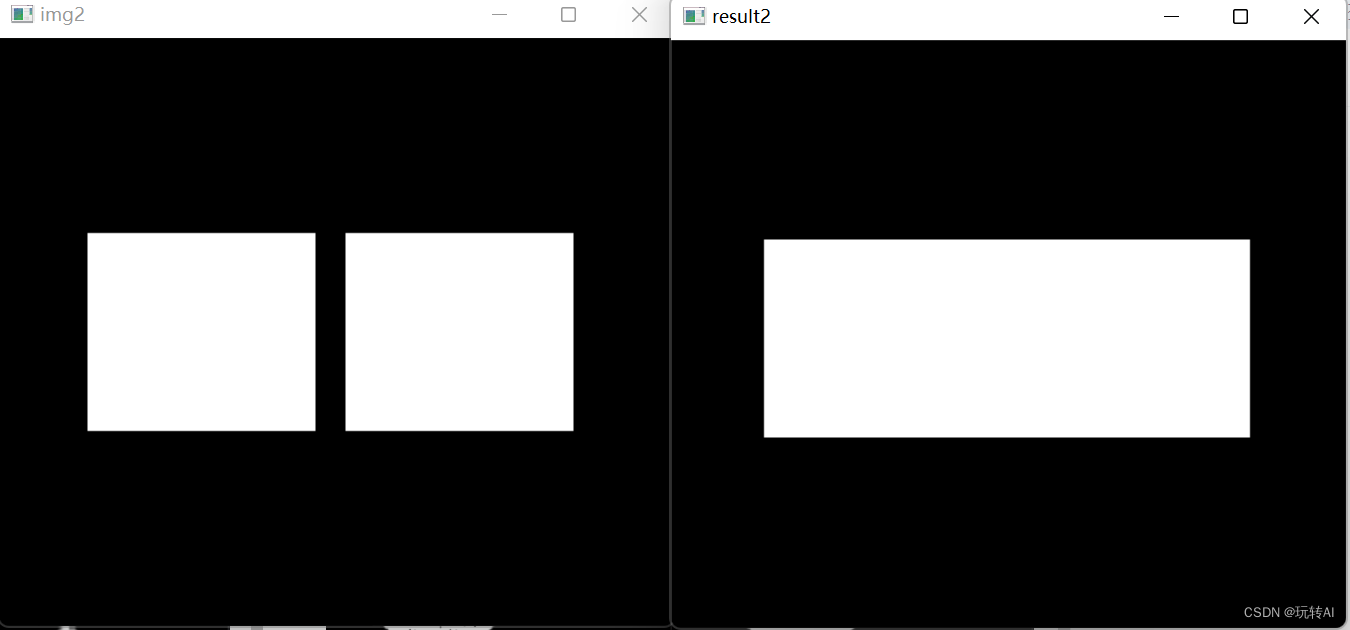
opencv基础-38 形态学操作-闭运算(先膨胀,后腐蚀)cv2.morphologyEx(img, cv2.MORPH_CLOSE, kernel)
闭运算是先膨胀、后腐蚀的运算,它有助于关闭前景物体内部的小孔,或去除物体上的小黑点,还可以将不同的前景图像进行连接。 例如,在图 8-17 中,通过先膨胀后腐蚀的闭运算去除了原始图像内部的小孔(内部闭合的…...
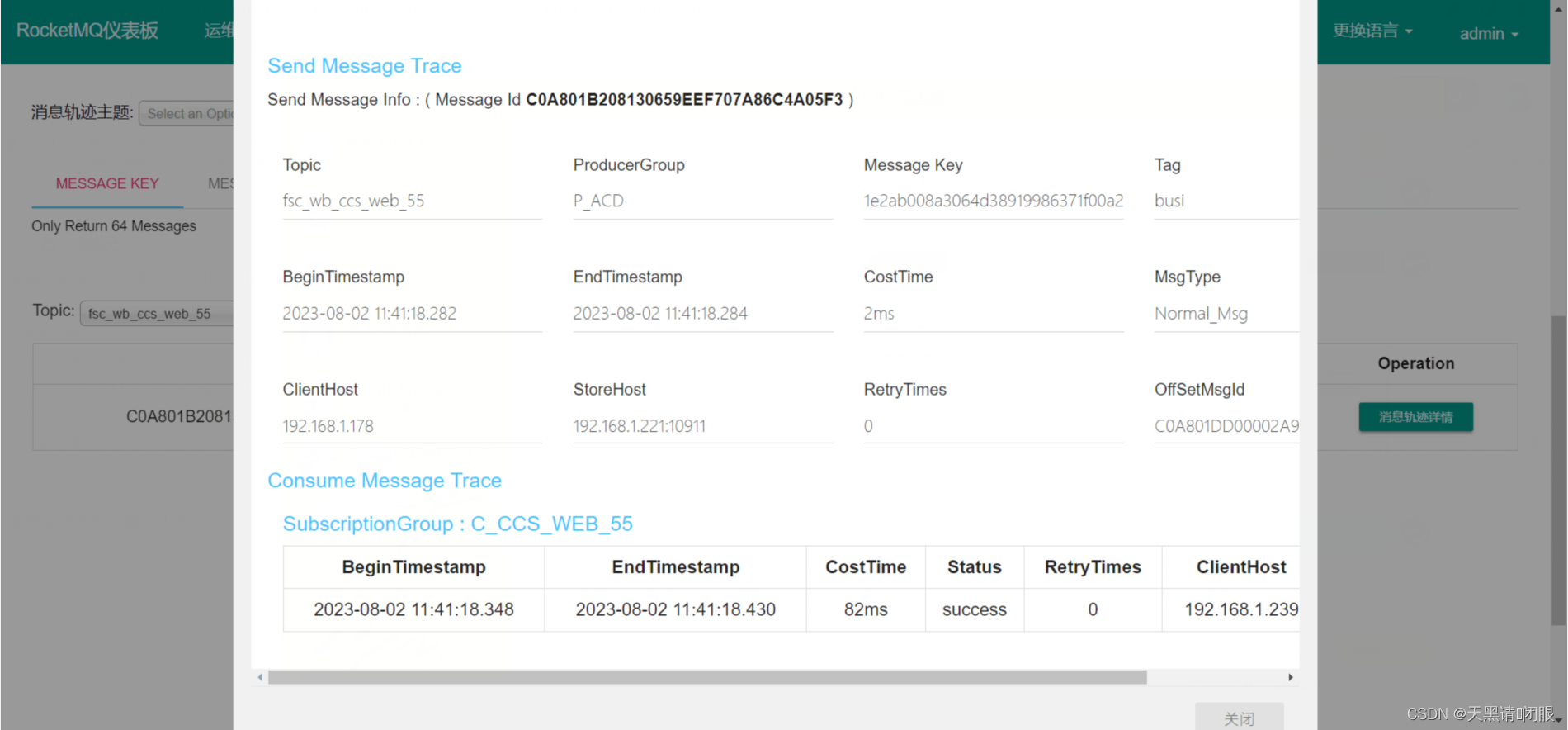
RocketMQ生产者和消费者都开启Message Trace后,Consume Message Trace没有消费轨迹
一、依赖 <dependency><groupId>org.apache.rocketmq</groupId><artifactId>rocketmq-spring-boot-starter</artifactId><version>2.0.3</version> </dependency>二、场景 1、生产者和消费者所属同一个程序 2、生产者开启消…...

JDV背后的技术-助力618 | 京东云技术团队
一、项目介绍 JDV(可视化大屏)是京东内部搭建可视化大屏的数据工具平台,内置10种模版特效,40种风格各异的图表、导航等组件。与集团其他数据工具打通,支持一站式、自助化、拖拽式搭建大屏,实现数据切换、联…...
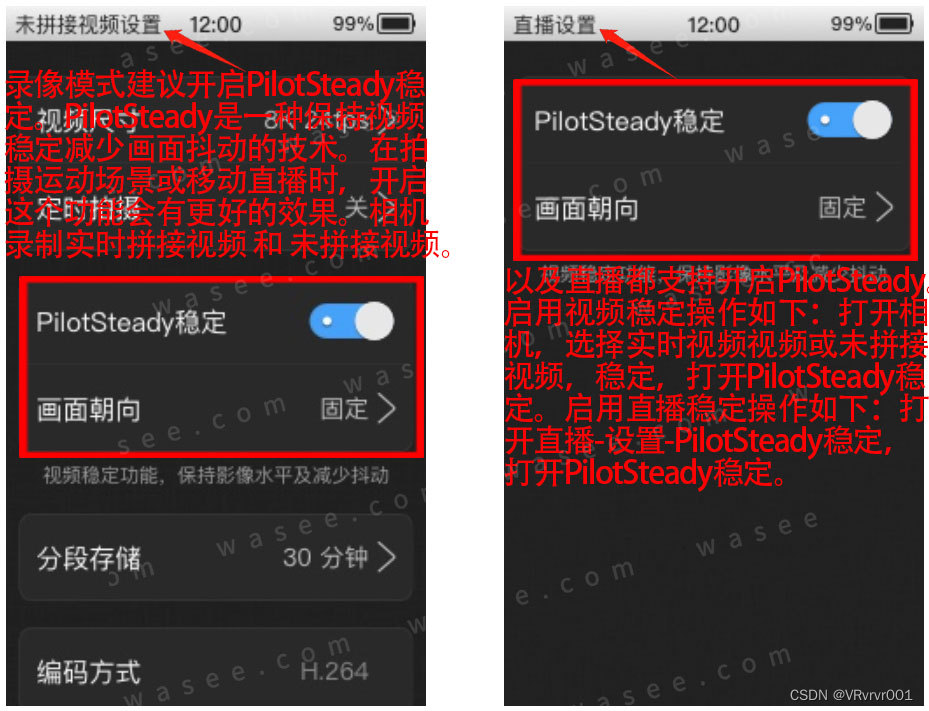
0基础学习VR全景平台篇 第78篇:全景相机-拍摄VR全景
新手入门圆周率科技,成立于2012年,是中国最早投身嵌入式全景算法研发的团队之一,亦是全球市场占有率最大的全景算法供应商。相继推出一体化智能屏、支持一键高清全景直播的智慧全景相机--Pilot Era和Pilot One,为用户带来实时畅享…...

Spring MVC简介与概述
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
)
java基础复习(第六日)
java基础复习(五) 1.是否了解类似 RabbitMQ.kalka 之类的队列服务? 请简述队列取务中的常见要素和使用场景? 了解,队列服务是一种应用间的通信方式,可以实现异步处理、应用解耦、流量削峰和消息通信等功能 队列服务的常见要素:…...
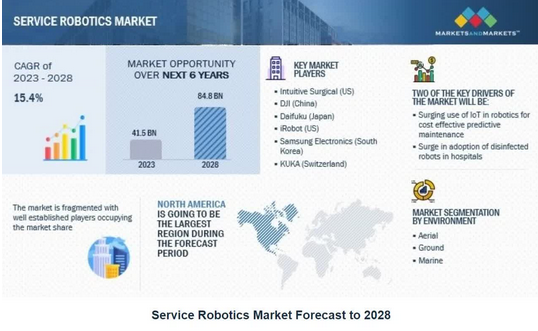
商用服务机器人公司【Richtech Robotics】申请纳斯达克IPO上市
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,总部位于美国内华达州拉斯维加斯由华人领导的商用服务机器人公司【Richtech Robotics】近期已向美国证券交易委员会(SEC)提交招股书,申请在纳斯达克IPO上市&am…...

关于nn.Embedding如何使用预定义词表
直接使用,则是没有pretrained的词表。 若要使用预定义词表,则可以用 pretrained_weight np.array(pretrained_weight) embeds.weight.data.copy_(torch.from_numpy(pretrained_weight))参考: https://wmathor.com/index.php/archives/1435/…...
怎么设置文件夹密码?文件夹密码设置方法合集
为文件夹设置密码可以有效地保护文件夹的数据安全,那么该怎么设置文件夹密码呢?下面我们来一起了解一下。 文件夹保护3000 想要简单快捷的为文件夹设置密码,那么,文件夹保护3000就是最佳的选择。它提供了3种文件夹保护方式&#…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
