跟我学C++中级篇——三五法则
一、三五法则
三五法则,这个叫着有点上头,说实话,这个三五法则,未来会不会变成三六或者四七法则,没人知道,反正现在是三五法则。在《c++Primer》第四版中,叫三法则,在第五版第13.1.4章节则叫做了三五法则。
什么是三五法则?分开来讲,三法则是指c++编译器会默认生成类的三个基本拷贝操作函数即:拷贝构造函数、拷贝赋值运算符和析构函数。五法则则是在前面的基础上,c++11后提供的移动构造函数和移动赋值运算符。这几个类一般情况下是一个整体,如果需要其中一个,其它也需要。
一般写c++程序的人员经常是写个构造函数就OK了,比如在Qt提供的自定义类中,就没有析构函数,就这意思。但你只定义了其中一个比如析构函数或者拷贝构造函数,程序也运行的很好。是的,这没有问题,因为基本上也遇不到故意去用这种意外情况的情况。(正如书所提到的只定义了析构函数,但未定义拷贝和赋值操作,浅拷贝造成的二次析构同一指针的问题)。
二、说明
1、需要显示定义的析构函数也需要定义拷贝构造函数和赋值构造函数(或者说定义其中一个,其它五个一般都要定义)
正如前面分析,对于合成的拷贝系列函数,会产生浅拷贝的问题,这时析构函数会产生多次释放同一内存指针的问题,也就UB问题产生了。但事实上基本上这种行为就是崩溃。
class A
{
public:char * s_ = nullptr;A(){s_ = new char[10];}~A(){delete s_;}
};int main(void)
{A a;A b(a);return 0;
}
这个问题并不罕见,在几乎所有的c++入门书籍中,都会提到类似问题,因为它更是用来说明拷贝构造函数的,但是基本上没有人会把其和析构函数联系起来。
2、需要拷贝操作的类也需要赋值操作,反之亦然
这个就很好理解了,朋友一生一起走(逻辑行为一致)。特别是在面试时,经常问这个行为到底调用拷贝构造还是赋值操作。这里重温一个小问题,为什么拷贝构造函数参数必须是一个引用,const有没有必要?前者是因为非引用会产生递归循环,编译错误;后才则不一定是必须的,但一直是这么做。
3、析构函数不可删除
因为删除析构函数会导致在栈上的对象无法释放,所以,它会产生一种奇妙的行为,如果不想让开发者在栈上使用这个对象就可以private它。换句话说,可以动态分配这个对象,并手动释放相关的资源。
4、如果类成员有删除或不可访问的析构函数(或拷贝、赋值),则类本身合成析构函数(拷贝、赋值)自动定义为删除的
这个法则的意思是严格限制定义规则,防止因为自动合成的拷贝系列函数产生漏洞。
class A
{
private:~A();
};
class B
{A a;
};
5、如果类对象有const或者引用成员则不能使用合成的拷贝赋值操作
这个好理解,就是对cv限定符的一种安全处理。
三、总结
正如人们经常讲的,有人在替你负重前行。这句话用在c++这不太恰当,但是大概意思相当。有的时候儿开发者可能什么都没有做,但为了保障基本的编译实现,c++标准还是要求编译器在后台要完成一些基础的动作。而且随着标准的发展,这些东西可能还会增加。看看c++11中推出的移动构造就明白了,没有什么一成不变的东西,要想更好的活在当下,就必须变革,这才是王道。
上周把大佬的名字搞错了,结果出了乌龙笑话。亏得众位兄弟及时指出,特此感谢。这些兄弟是:
多喝水多运动,孤蓬,Emma,捉虫少年小鹏向您发起挑战。
再次感谢上面的朋友,并对乌龙事件表示歉意。
相关文章:

跟我学C++中级篇——三五法则
一、三五法则 三五法则,这个叫着有点上头,说实话,这个三五法则,未来会不会变成三六或者四七法则,没人知道,反正现在是三五法则。在《cPrimer》第四版中,叫三法则,在第五版第13.1.4章…...
aardio:用 WebView 模仿 mdict 界面
aardio:用 WebView 模仿 mdict 界面 import win.ui; /*DSG{{*/ mainForm win.form(text"aardio2";right889;bottom467) mainForm.add( button{cls"button";text"go";left335;top22;right399;bottom41;z2}; button2{cls"button…...

linq中的操作符
LINQ(Language Integrated Query)是一种用于.NET平台的查询语言,用于查询和操作各种数据源,如集合、数据库和XML。LINQ提供了一组标准查询操作符,用于执行各种查询操作。 LINQ(Language Integrated Query&…...
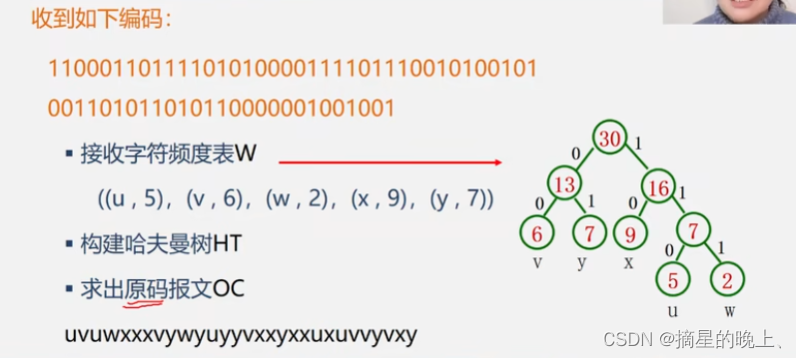
数据结构【哈夫曼树】
哈夫曼树 哈夫曼树的概念哈夫曼树的构造构造算法的实现哈夫曼树应用哈夫曼编码哈夫曼编码的算法实现 哈夫曼树的概念 最优二叉树也称哈夫曼 (Huffman) 树,是指对于一组带有确定权值的叶子结点,构造的具有最小带权路径长度的二叉树。权值是指一个与特定结…...
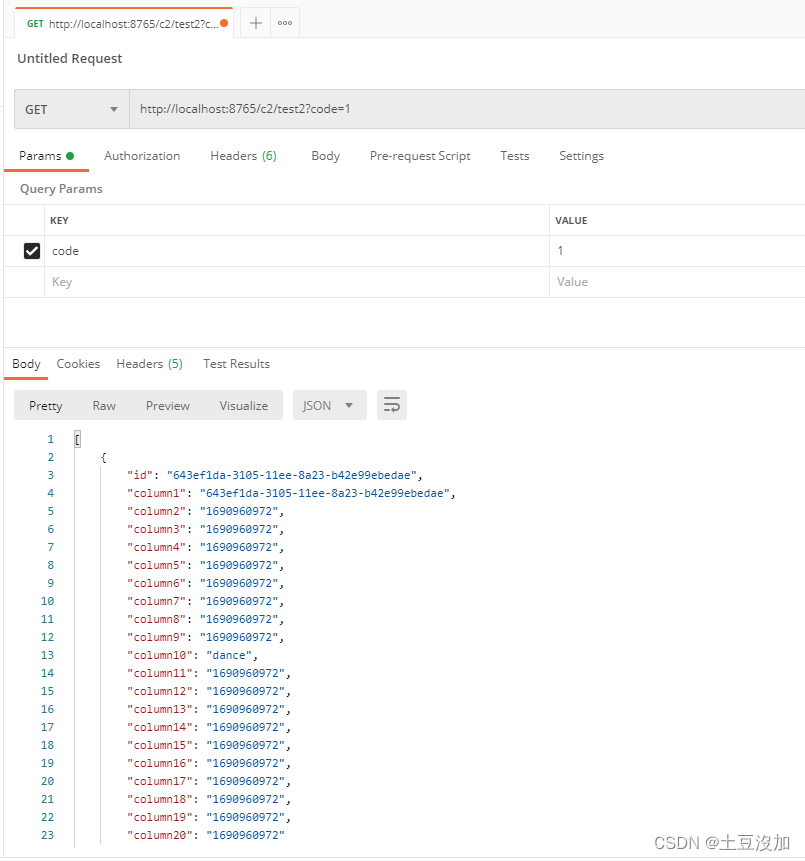
SpringMVC基于SpringBoot的最基础框架搭建——包含数据库连接
SpringMVC基于SpringBoot的最基础框架搭建——包含数据库连接 背景目标依赖配置文件如下项目结构如下相关配置如下启动代码如下Controller如下启动成功接口调用成功 背景 工作做了一段时间,回忆起之前有个公司有线下笔试,要求考生做一个什么功能&#x…...

deepspeed zero3
zero3。它是纵向切分权重(intra-layer,每一层的权重切成n块)。但是这样会增加通讯时间。你可以根据自己的模型,估算下切分后的通讯量和通讯时间。其次,pipeline并行一般指横向切分权重(inter-layer…...
代驾小程序怎么做
代驾小程序是一款专门为用户提供代驾服务的手机应用程序。它具有以下功能: 1. 预约代驾:代驾小程序允许用户在需要代驾服务时提前进行预约。用户可以选择出发地点、目的地以及预计用车时间,系统会自动匹配最合适的代驾司机,并确保…...

探索 AJAX 技术:实现动态数据交互的前端利器
简介: AJAX(Asynchronous JavaScript and XML)技术在 Web 前端开发中扮演着重要的角色,它通过异步通信和动态内容更新,为用户带来更好的交互体验。本篇笔记将详细探索 AJAX 技术,并通过生动的代码演示来展示…...
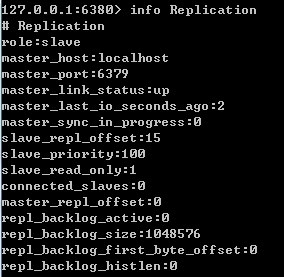
深度学习Redis(3):主从复制
前言 在前面的两篇文章中,分别介绍Redis内存模型和Redis持久化 在Redis的持久化中曾提到,Redis高可用的方案包括持久化、主从复制(及读写分离)、哨兵和集群。其中持久化侧重解决的是Redis数据的单机备份问题(从内存到…...

php笔记1
php环境 PHP作为一种服务器端脚本语言,可以在各种操作系统上运行。搭建PHP网站的环境,你需要以下几个要素: Web服务器:常见的选择有Apache、Nginx和IIS。你需要安装和配置其中一个服务器软件。PHP解释器:PHP是一种解…...

2023 ChinaJoy 圆满闭幕,FairGuard游戏加固亮相 BTOB 展区
提振行业 产业复苏 2023年7月28日至7月31日,第二十届中国国际数码互动娱乐展览会( ChinaJoy)于上海新国际博览中心圆满举办。本届ChinaJoy作为疫情结束后的第一个国际性数字娱乐领域的重要产业盛会,对于提振行业信心、加快产业复苏、增进国际间的交流与…...
数据规约策略
有很多概念平时一直在说,但是具体的应用场景却一直不明确,这会导致我们在实际应用过程中对应该使用的方法不够明确,在此对常用的几种数据挖掘方法使用场景进行分类和整合。 数据降维 为什么要降维 数据稀疏,维度高高维数据采用…...

服务器带宽独享跟共享有什么区别103.36.166.x
独享带宽 独享带宽针对对带宽有较高的要求,其业务的内容和性质决定只有使用独立的带宽资源才能满足品质的需求,而这种只给单独客户使用的带宽资源称为独享带宽. 使用独享带宽,整个带宽资源归属于一个客户 独享带宽的优点是可自由使用带宽量…...

【cluster_block_exception】写操作elasticsearch索引报错
【cluster_block_exception】操作elasticsearch索引b报错 背景导致原因:解决方法: 背景 今天线上elk的数据太多,服务器的空间不足了。所以打算删除一些没用用的数据。我是用下面的request: POST /{index_name}/_delete_by_query…...
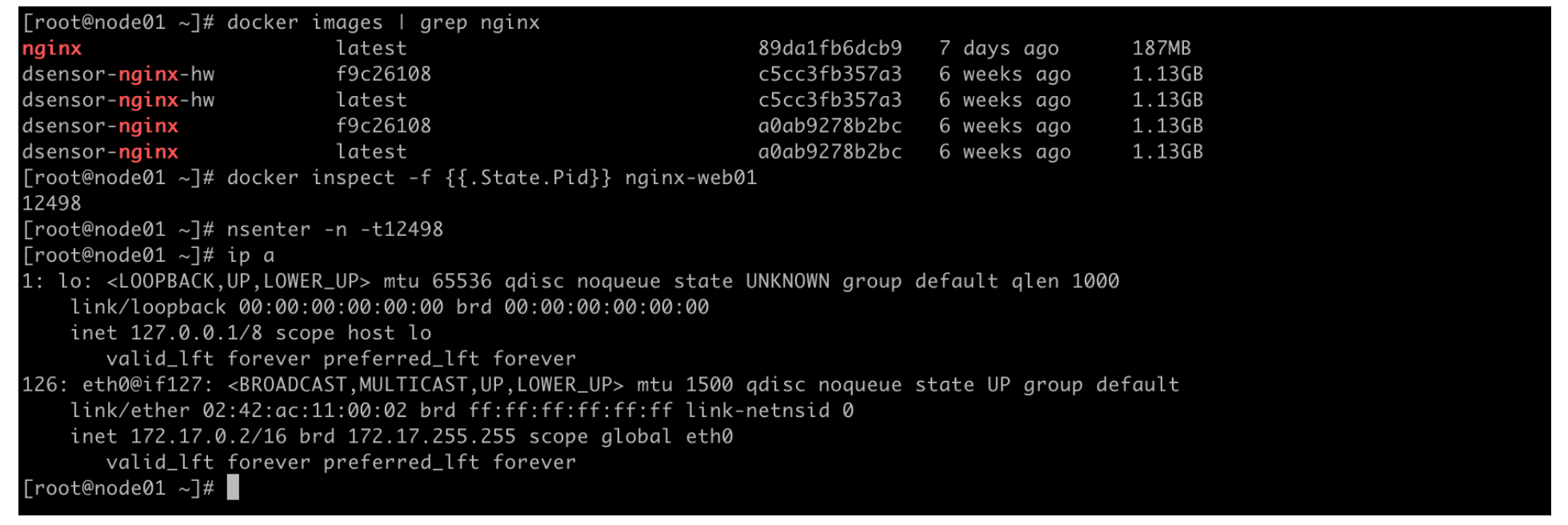
chaitin-Nginx+Docker
Nginx实战 任务一 1、源码包安装NGINX A,搭建Web Server,任意HTML页面,其8080端口提供Web访问服务,截图成功访问http(s)😕/[Server1]:8080并且回显Web页面 官网地址:http://nginx.org/en/download.html 步骤…...

具体面试题
具体面试题 Java 基础 JDK 和 JRE 有什么区别? 和 equals 的区别是什么? 两个对象的 hashCode() 相同,则 equals() 也一定为 true,对吗? final 在 java 中有什么作用? java 中的 Math.round(-1.5) 等…...

Logback ThresholdFilter LevelFilter
当我们需要对日志的打印要做一些范围的控制的时候,通常都是通过为各个Appender设置不同的Filter配置来实现。在Logback中自带了两个过滤器实现: ch.qos.logback.classic.filter.LevelFilter和 ch.qos.logback.classic.filter.ThresholdFilter,…...
python+django+mysql项目实践二(前端及数据库)
python项目实践 环境说明: Pycharm 开发环境 Django 前端 MySQL 数据库 Navicat 数据库管理 前端模板 添加模板 在templates下创建 views文件中添加 创建数据库 连接数据库 在setting文件中进行配置 创建表...
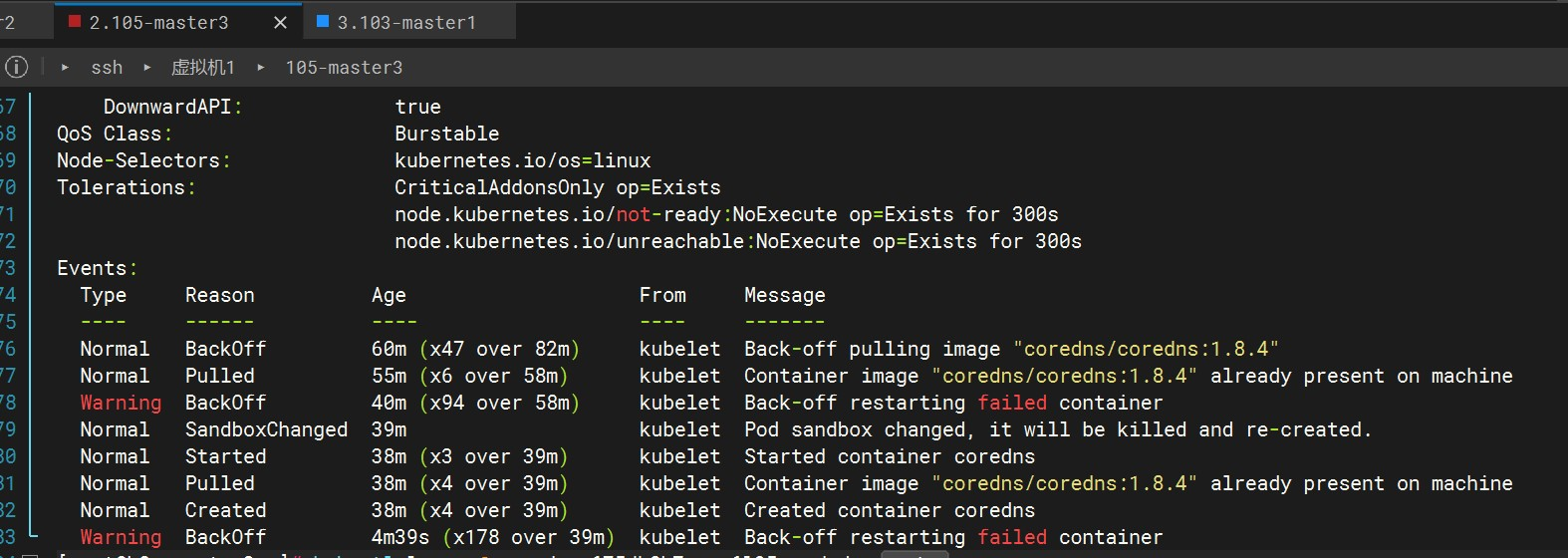
Kubernetes高可用集群二进制部署(五)kubelet、kube-proxy、Calico、CoreDNS
Kubernetes概述 使用kubeadm快速部署一个k8s集群 Kubernetes高可用集群二进制部署(一)主机准备和负载均衡器安装 Kubernetes高可用集群二进制部署(二)ETCD集群部署 Kubernetes高可用集群二进制部署(三)部署…...
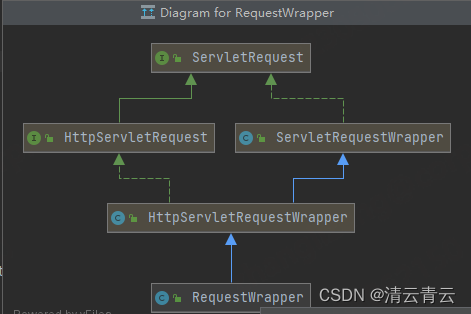
拦截器对接口细粒度权限校验
文章目录 一、逻辑分析二、校验规则1.规则类型2.规则划分3.规则配置信息4.规则案例说明5.规则加载 三、拦截器定义1.自定义拦截器2.注册拦截器 四、获取请求参数1.获取get提交方式参数2.获取post提交方式参数(1)定义RequestWrapper类(2&#…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
