C++数据结构之平衡二叉搜索树(一)——AVL的实现(zig与zag/左右双旋/3+4重构)
本文目录
- 00.BBST——平衡二叉搜索树
- 01.AVL树
- 02.AVL的插入
- 2.1单旋——zig 与 zag
- 2.2插入节点后的单旋实例
- 2.3手玩小样例
- 2.4双旋实例
- 2.5小结
- 03.AVL的删除
- 3.1单旋删除
- 3.2双旋删除
- 3.3小结
- 04.3+4重构
- 05.综合评价AVL
- 5.1优点
- 5.2缺点
- 06.代码
- 注意
- 插入算法
- 删除算法
- 完整代码:AVL.h
00.BBST——平衡二叉搜索树
本文是介绍众多平衡二叉搜索树(BBST)的第一篇——介绍AVL树。故先来引入BBST的概念。由于上一篇介绍的二叉搜索树(BST)在极度退化的情况下,十分不平衡,不平衡到只朝一侧偏,成为一条链表,复杂度可达 O ( n ) O(n) O(n),所以我们要在“平衡”方面做一些约束,以防我们的树结构退化得那么严重。
具体来说,含 n n n个节点,高度为 h h h的BST,若满足 h = O ( l o g 2 n ) h=O(log_2 n) h=O(log2n),则称为称为平衡二叉搜索树。
01.AVL树
AVL树是一种BBST(稍后会证明)。它约束自己是否平衡,主要靠一个指标——平衡因子。定义:平衡因子=左子树高度-右子树高度。如果满足 − 2 < 全部平衡因子 < 2 -2<全部平衡因子<2 −2<全部平衡因子<2,则该AVL树处于平衡状态;否则,需要靠一系列措施,将其恢复平衡。
首先先证明AVL树满足BBST的要求,即 h = O ( l o g 2 n ) h=O(log_2 n) h=O(log2n)(下式)。我们可转而证明n=Ω(Φh)(即,AVL的节点数不会太少)

[结论] 高度为 h h h的AVL Tree 至少有 f i b ( ( h + 3 ) − 1 fib((h+3)-1 fib((h+3)−1 个节点
[证明]



02.AVL的插入
插入一个节点会导致一串祖先的失衡,删除一个节点至多导致一个祖先失衡。但是,通过后续代码就可发现,删除节点比插入节点复杂的多。原因是,插入节点只要调整好了一处,这条路径上的所有祖先都可平衡,复杂度是
O(1)。而删除节点是,调整好了一处平衡,另一处就会不平衡,自下而上层层调整,复杂度是O(n)。
2.1单旋——zig 与 zag
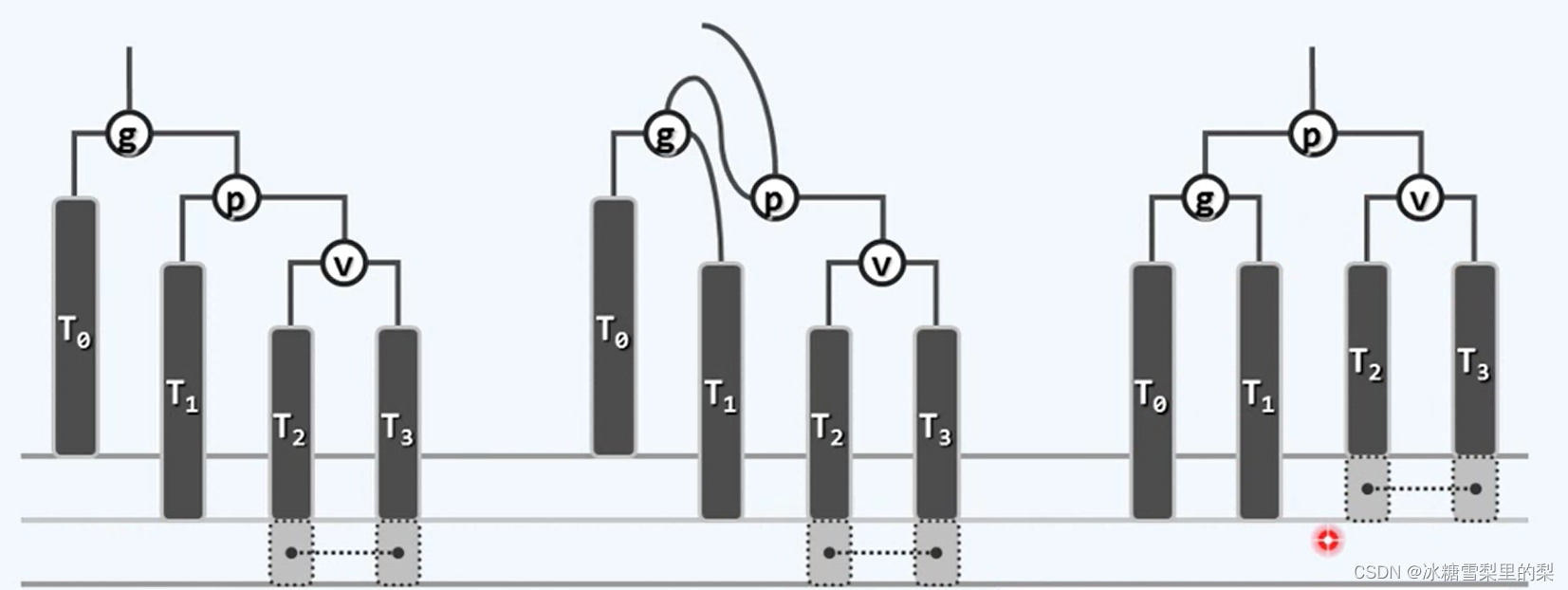
zig 与 zag 分别对应右单旋和左单旋。单旋的操作改变的是两个节点的相对位置。改变的是三条线:一上一下一子树。新树根上行指向原根,新树根原子树给到原根。如下图,V到Y那去,Y到C那去。

2.2插入节点后的单旋实例
在下图 处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈一条线,而非“之”字,所以用单旋调整(之字形对应双旋)。具体来说,对g左单旋。
处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈一条线,而非“之”字,所以用单旋调整(之字形对应双旋)。具体来说,对g左单旋。
2.3手玩小样例
例题:将1,2,3,4,5,6依次插入空的AVL Tree,最终AVL Tree长成什么样?
[过程]首先正常插入1,2;插入3时,1是第一个发现不平衡的节点,zag(1),即对1进行左单旋,成功解决;正常插入4

插入5时,3是第一个发现不平衡的节点,zag(3),即对3进行左单旋,成功解决

插入6时,2是第一个发现不平衡的节点,zag(2),即对2进行左单旋,成功解决

2.4双旋实例
双旋的操作改变的是三个节点的相对位置。分为两种情况——zig-zag与zag-zig。
在下图 处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈“之”字,所以用双旋。具体来说,先zig§,再zag(g).
处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈“之”字,所以用双旋。具体来说,先zig§,再zag(g).

2.5小结
AVL树中插入节点引发失衡,经旋转调整后重新平衡,此时包含节点g,p,v的子树高度是不变的,子树高度复原,更高祖先也必平衡,全树复衡。故在AVL树中修正插入节点引发的失衡不会出现失衡传播。
03.AVL的删除
删除一个节点至多导致一个祖先失衡。
3.1单旋删除

3.2双旋删除

3.3小结
AVL树中删除节点引发失衡,经旋转调整后重新平衡,此时包含节点g,p,v的子树高度有可能不变也有可能减小1,故在AVL树中修正删除节点引发的失衡有可能出现失衡传播。
04.3+4重构
通过观察以上插入和删除的结果示意图,发现结构是一样的——三个节点按顺序呈三角形,四个子树按原来的顺序分别挂在两个孩子节点的下边。(如下图)

那我们就不必关注具体的技巧了,而是将三个节点和四个子树拆开,像暴力组装魔方那样(先拆散)拼上。
template <typename T>
BinNode<T> * BST<T>::connect34(BinNode<T> * a, BinNode<T> * b, BinNode<T> * c, BinNode<T> * T1, BinNode<T> * T2, BinNode<T> *T3, BinNode<T> * T4)
{b->left = a; b->right = c;a->left = T1; a->right = T2;c->left = T3; c->right = T4;a->parent = b; c->parent = b;if (T1) T1->parent = a;if (T2) T2->parent = a;if (T3) T3->parent = c;if (T4) T4->parent = c;a->updateHigh(); b->updateHigh(); c->updateHigh();return b;
}template <typename T>
BinNode<T> * BST<T>::rotateAt(BinNode<T> * v)
{BinNode<T> * p = v->parent;BinNode<T> * g = p->parent;BinNode<T> * T1, *T2, *T3, *T4, *a, *b, *c;if (p == g->left && v == p->left){a = v; b = p; c = g;T1 = v->left; T2 = v->right; T3 = p->right; T4 = g->right;}else if (p == g->left && v == p->right){a = p; b = v; c = g;T1 = p->left; T2 = v->left; T3 = v->right; T4 = g->right;} else if (p == g->right && v == p->left){a = g; b = v; c = p;T1 = g->left; T2 = v->left; T3 = v->right; T4 = p->right;}else{a = g; b = p; c = v;T1 = g->left; T2 = p->left; T3 = v->left; T4 = v->right;}b->parent = g->parent; //向上链接return connect34(a, b, c, T1, T2, T3, T4);}
05.综合评价AVL
5.1优点
- 查找、插入、删除,最坏时间复杂度为 O ( l o g n ) O(logn) O(logn)
- O ( n ) O(n) O(n)的存储空间
5.2缺点
- 需要额外维护高度或平衡因子这一指标(后续Splay Tree可改善这一问题)
- 删除操作后,最多需旋转 Ω ( l o g n ) \Omega(logn) Ω(logn)次
- 单次动态调整后,全树拓扑结构的变化量可能高达 Ω ( l o g n ) \Omega(logn) Ω(logn) (RedBlack Tree可缩到 O ( 1 ) O(1) O(1))
谢谢观看~
06.代码
注意
fromParentTo()是根节点的情况connect34()向上链接别忘
插入算法
为什么不用现成的BST::insert(val)? BST::insert自带更新一串高度,旋转调整之后还得把这一串更新回来。
BinNode<T> * insert(T const & val){BinNode<T> * & X = BST<T>::search(val);if (!X){X = new BinNode<T>(val, BST<T>::hot); BinTree<T>::size++;BinNode<T> * X_copy = X;while (X_copy && AvlBalanced(X_copy)){X_copy->updateHigh();X_copy = X_copy->parent;}if (X_copy) //说明是因为遇到了不平衡节点才退出了while,现在解决不平衡问题{BinNode<T> * & tmp = BinTree<T>::fromParentTo(X_copy);tmp = BST<T>::rotateAt(tallerChild(tallerChild(X_copy))); // 内部自带单个节点更新高度}return X;}}
删除算法
受限于BST::remove的返回值仅仅是bool,所以用底层的removeAt. removeAt的返回值是接替者,但有时,接替者是NULL。还好有BST::hot,存放被删节点的父亲。实际上,BST::remove的更新高度也是从hot开始的
bool remove(T const & val) {BinNode<T> * & X = BST<T>::search(val);if (!X) return false;else{BST<T>::removeAt(X, BST<T>::hot);BinTree<T>::size--;// 与insert不同的是,remove可能要调整很多次for (BinNode<T> * g = BST<T>::hot; g; g = g->parent){int i = BF(g);if (!AvlBalanced(g)){BinNode<T> * & tmp = BinTree<T>::fromParentTo(g);tmp = BST<T>::rotateAt(tallerChild(tallerChild(g))); }else g->updateHigh();}return true;}}
完整代码:AVL.h
# pragma once
# include "BST.h"# define BF(x) (int)(getHigh(x->left) - getHigh(x->right))
# define AvlBalanced(x) ( -2 < BF(x) && BF(x) < 2 )template <typename T>
BinNode<T> * tallerChild(BinNode<T> * x)
{return (getHigh(x->left) > getHigh(x->right)) ? x->left : x->right;
}template <typename T>
class AVL :public BST<T>
{public:bool remove(T const & val) {BinNode<T> * & X = BST<T>::search(val);if (!X) return false;else{BST<T>::removeAt(X, BST<T>::hot);BinTree<T>::size--;// (可优化:直到到某祖先,高度不变,停止上行。那就要在刚刚更新高度时记录中途退出的位置,以便在此处判断)for (BinNode<T> * g = BST<T>::hot; g; g = g->parent){int i = BF(g);if (!AvlBalanced(g)){BinNode<T> * & tmp = BinTree<T>::fromParentTo(g);tmp = BST<T>::rotateAt(tallerChild(tallerChild(g))); // 内部自带单个节点更新高度}else g->updateHigh();}return true;}}BinNode<T> * insert(T const & val){BinNode<T> * & X = BST<T>::search(val);if (!X){X = new BinNode<T>(val, BST<T>::hot); //这一句话将两个关系连接BinTree<T>::size++;BinNode<T> * X_copy = X;while (X_copy && AvlBalanced(X_copy)){X_copy->updateHigh();X_copy = X_copy->parent;}if (X_copy) //说明是因为遇到了不平衡节点才退出了while,现在解决不平衡问题{BinNode<T> * & tmp = BinTree<T>::fromParentTo(X_copy);tmp = BST<T>::rotateAt(tallerChild(tallerChild(X_copy))); // 内部自带单个节点更新高度}return X;}}
};感谢观看~
附上前传:
C++数据结构之BinaryTree(二叉树)的实现
C++数据结构之BST(二叉搜索树)的实现
相关文章:

C++数据结构之平衡二叉搜索树(一)——AVL的实现(zig与zag/左右双旋/3+4重构)
本文目录 00.BBST——平衡二叉搜索树01.AVL树02.AVL的插入2.1单旋——zig 与 zag2.2插入节点后的单旋实例2.3手玩小样例2.4双旋实例2.5小结 03.AVL的删除3.1单旋删除3.2双旋删除3.3小结 04.34重构05.综合评价AVL5.1优点5.2缺点 06.代码注意插入算法删除算法完整代码:…...
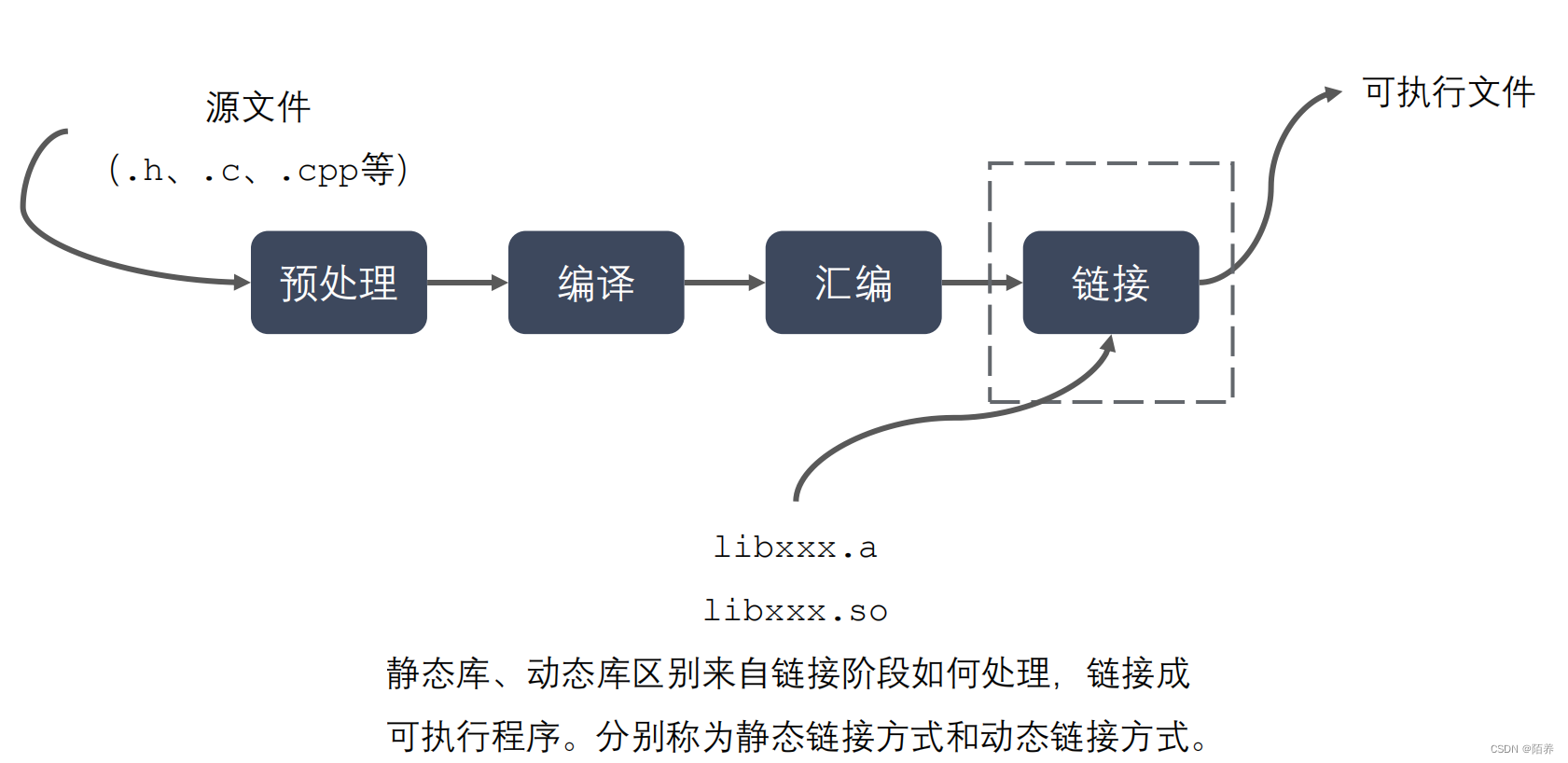
静态库和动态库
库文件 库文件是计算机上的一类文件,可以简单的把库文件看成一种代码仓库,它提供给使用者一些可以直接拿来用的变量、函数或类。 库是特殊的一种程序,编写库的程序和编写一般的程序区别不大,只是库不能单独运行。库文件有两种&a…...

用于Voronoi图构建的Fortune算法的C++实现
Voronoi图是一种在计算几何中广泛使用的数据结构,它可以用于解决最近邻搜索、路径规划等问题。在这篇文章中,我们将探讨一种用于构建Voronoi图的高效算法——Fortune算法,并提供其C实现。 一、Voronoi图简介 Voronoi图是由一组点在平面上生…...

笔记汇总 | 斯坦福 CS229 机器学习
文章目录 前言课程参考文章推荐阅读 前言 本文为斯坦福大学 CS229 机器学习课程学习笔记 本文主体部分转载自黄海广博士,文末已给出链接,大家有兴趣可以直接访问笔记首页,下载对应课程资料及作业代码 课程官网:CS229: Machine …...

git 版本管理工具 学习笔记
git 学习笔记 目录 一、git是什么 二、创建仓库 三、工作区域和文件状态 四、添加和提交文件 五、回退版本 (了解) 六、查看差异 七、删除文件 八、.gitignore文件(了解) 九、github ssh-key配置 十、本地仓库和远程仓库内…...
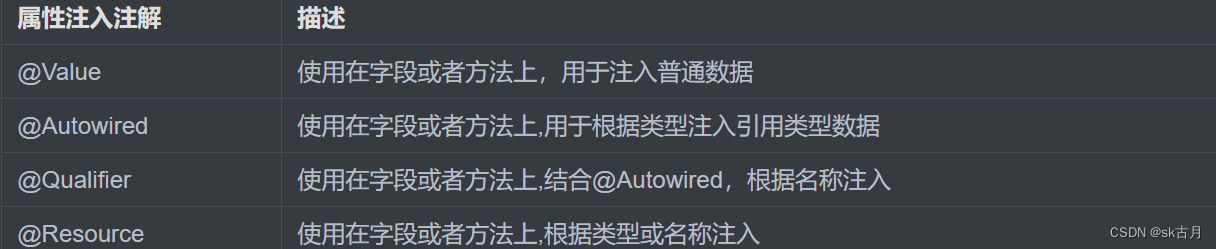
Bean基本注解开发和Bean依赖注入注解开发
目录 1.Bean基本注解开发 Component Scorelazy PostConstruct和PreDestroy RepositoryServiceController 2.Bean依赖注入注解开发 Value Autowired Qualifier Resource 扩展AutoWired 1.Bean基本注解开发 基本Bean注解,主要是使用注释的方式替代原有xml的…...
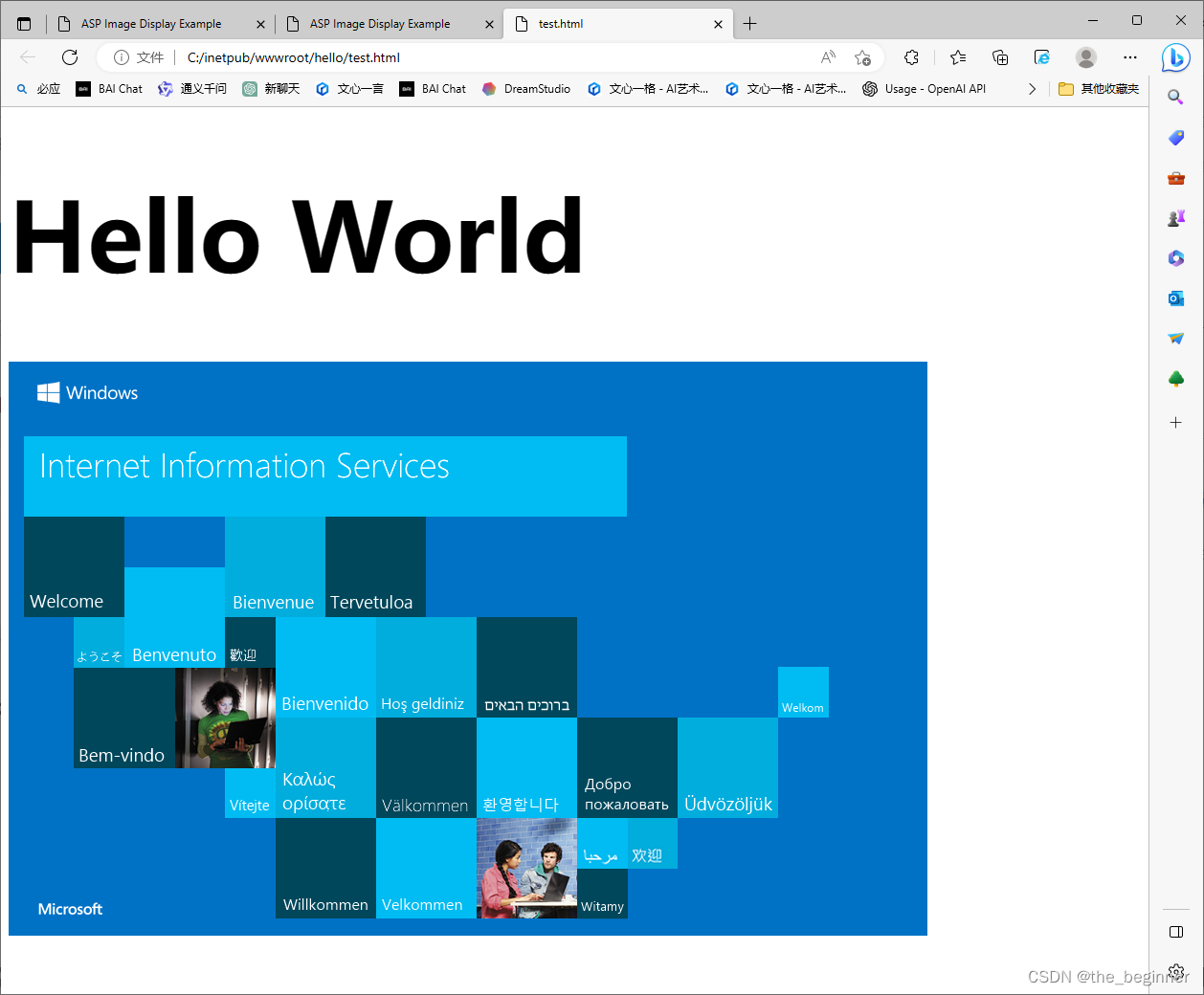
使用IIS服务器搭建一个网站
参考文章 使用IIS(Internet Information Services)服务器搭建一个网站相对来说是比较简单的。以下是基本的步骤: 安装IIS: 首先,确保你的操作系统已经安装了IIS。在大多数Windows版本中,IIS都是可选安装项…...
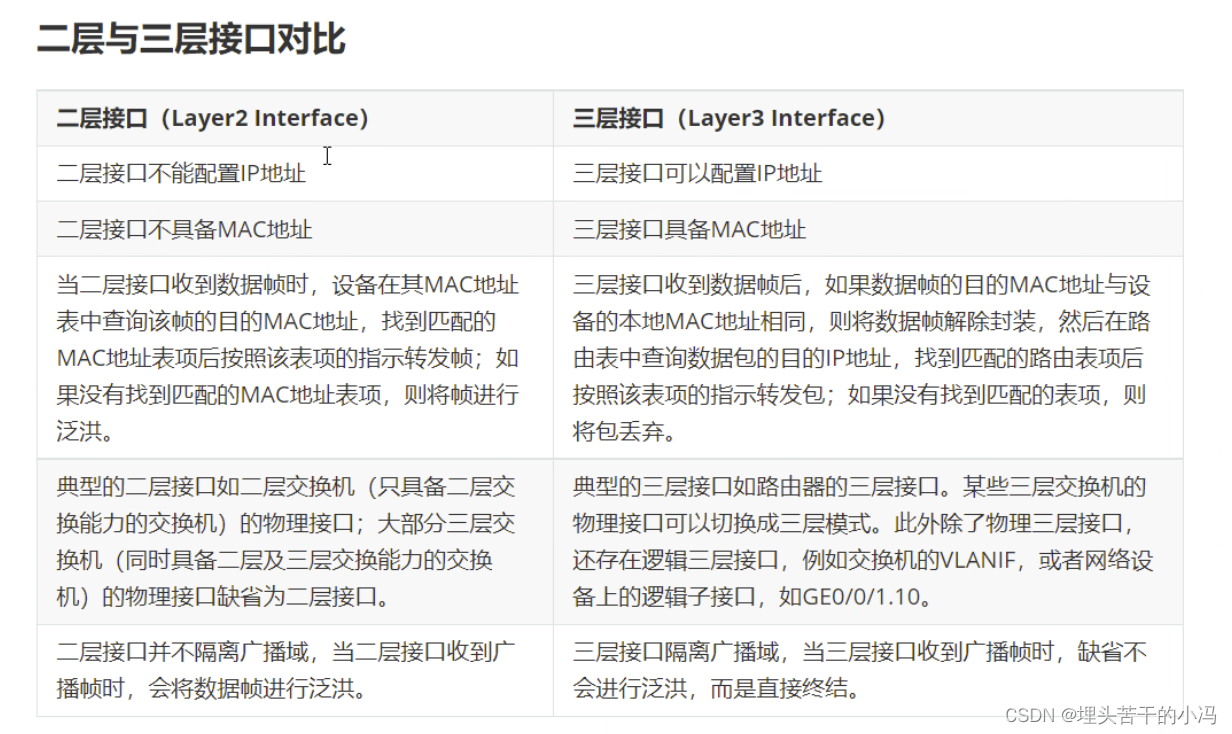
HCIP 三层交换机
一、实现VLAN间通信 在传统的交换机组网中,默认所有网络都处于同一个广播域,带来了许多问题,VLAN技术的提出,满足了二层组网隔离广播域需求,使得属于不同的VLAN间网络无法通信,但不同VLAN之间又存在着互相…...
第二章小结)
利用python 进行数据分析(第三版)第二章小结
利用python 进行数据分析(第三版)第二章小结 由于是闲暇时间看的,且为读书笔记,所以只会写一些心得和容易混淆的知识,简单知识将不在重复 在变量或者函数后使用?可以查看详细信息。?还有最后一个用途,即…...

【ASP.NET MVC】使用动软(四)(12)
一、筛选器类和Cookie实现路由 需解决的问题: 网站登录往往需要用户名密码验证,为避免重复验证,一般采用Cookie 、Session等技术来保持用户的登录状态: Session是在服务端保存的一个数据结构,用来跟踪用户的状态&…...
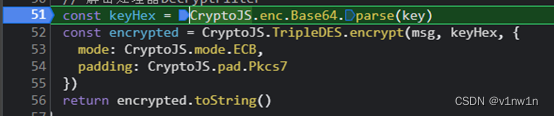
【web逆向】全报文加密及其登录流程的分析案例
aHR0cHM6Ly9oZWFsdGguZWxkZXIuY2NiLmNvbS9zaWduX2luLw 涉及加密库jsencrypt 定位加密点 先看加密的请求和响应: 全局搜索加密字段jsondata,这种非特定参数的一般一搜一个准,搜到就是断点。起初下的断点没停住,转而从调用栈单步…...

MyBatis枚举映射类讨论
前言 本篇需要对于MyBatis有一定的认识,而且只是针对于TypeHandler接口来讨论,暂不讨论其他方面的问题 TypeHandler概叙 TypeHandler是MyBatis设计的一个用于参数的接口,你们会不会很好奇MyBatis是如何把整形,时间,字符…...
微信开发之朋友圈自动点赞的技术实现
简要描述: 朋友圈点赞 请求URL: http://域名地址/snsPraise 请求方式: POST 请求头Headers: Content-Type:application/jsonAuthorization:login接口返回 参数: 参数名必选类型说明wId…...

Linux命令200例:sed对文本进行修改、替换和删除等操作的强大工具(常用)
🏆作者简介,黑夜开发者,全栈领域新星创作者✌。CSDN专家博主,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师,项目技术负责人。 &…...

python 合并多个excel文件
使用 openpyxl 思路: 读取n个excel的文件,存储在一个二维数组中,注意需要转置。将二维数组的数据写入excel。 安装软件: pip install openpyxl源代码: import os import openpyxl # 将n个excel文件数据合并到一个…...

【Docker】性能测试监控平台搭建:InfluxDB+Grafana+Jmeter+cAdvisor
前言 在做性能测试时,如果有一个性能测试结果实时展示的页面,可以极大的提高我们对系统性能表现的掌握程度,进而提高我们的测试效率。但是我们每次打开Jmeter都会有几个硕大的字提示别用GUI模式进行负载测试,而且它自带的监视器效…...
wordpress日主题Ripro9.0最新二开修正源码下载+美化包和插件
日主题Ripro9.0最新二开升级修正源码美化包和插件,RiPro9.0的二开版本新模板,包含2个美化包和全屏水印以及防复制插件。 模板和美化包路径:\wp-content\themes 插件路径:\wp-content\plugins,有兴趣的自行去体验吧...

fib Model Code史海拾贝
文章目录 0. 背景1. 强度等级不一致(20230807)1.1 问题描述(20230807)1.2 问题探索 0. 背景 本文主要记录在学习了解ModelCode的过程中产生的问题。当然,主要是我个人认为有意思的地方。欢迎有共同兴趣的网友留言一起…...
6.7.tensorRT高级(1)-使用onnxruntime进行onnx模型推理过程
目录 前言1. python-ort2. C-ort总结 前言 杜老师推出的 tensorRT从零起步高性能部署 课程,之前有看过一遍,但是没有做笔记,很多东西也忘了。这次重新撸一遍,顺便记记笔记。 本次课程学习 tensorRT 高级-使用 onnxruntime 进行 on…...

360未来安全研究院笔试题
笔试时间:2020.04.16,15:00-17:30。 岗位:Linux 安全开发工程师(实习生) 题型: 能力测试——逻辑题(20个5分=100分) 专业测试——客观题(40个2分=80分) 专业测试——在线编程题(2个25分=50分) 逻辑题 一共40道题目,很多逻辑推断题,包含数字找规律和图片找…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
