当前位置： 首页 > news >正文

opencv读取MP4文件和摄像头数据

news 2026/2/10 2:55:44

文章目录

  • 前言
  • 一、waitKey函数
  • 二、VideoCapture类
  • 总结

前言

本篇文章来讲解opencv读取MP4文件和摄像头数据，opencv主要用于处理图像数据那么本篇文章就来讲解opencv读取MP4文件和摄像头数据。

一、waitKey函数

waitKey()函数是OpenCV中常用的一个函数，它用于等待用户按键输入，并返回用户按下的键值。下面我将为您详细解释waitKey()函数的功能和使用。

waitKey()函数的基本语法如下：

int waitKey(int delay = 0);

参数说明：

delay：表示等待按键的时间（以毫秒为单位）。默认值为0，

相关文章：

opencv读取MP4文件和摄像头数据

文章目录 前言一、waitKey函数二、VideoCapture类总结前言 本篇文章来讲解opencv读取MP4文件和摄像头数据，opencv主要用于处理图像数据那么本篇文章就来讲解opencv读取MP4文件和摄像头数据。 一、waitKey函数 waitKey()函数是OpenCV中常用的一个函数，它用于等待用户按键输…...

编程日记 2023/8/8 6:53:52

Qt实现自定义QDoubleSpinBox软键盘

在Qt应用程序开发中，经常会遇到需要自定义输入控件的需求。其中，对于QDoubleSpinBox控件，如果希望在点击时弹出一个自定义的软键盘，以便用户输入数值，并将输入的值设置给QDoubleSpinBox，该如何实现呢&#…...

编程日记 2023/8/8 6:52:49

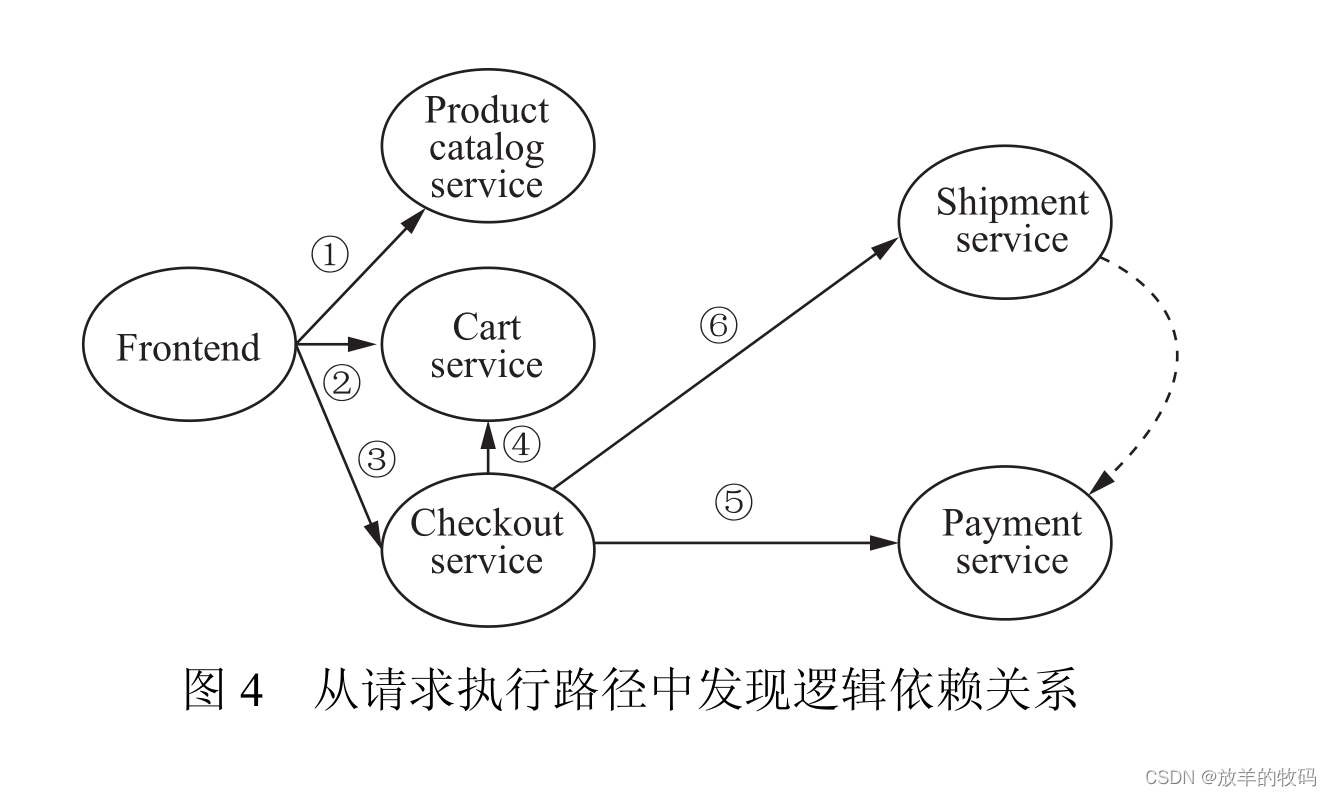
小研究 - 微服务系统服务依赖发现技术综述（一）

微服务架构得到了广泛的部署与应用, 提升了软件系统开发的效率, 降低了系统更新与维护的成本, 提高了系统的可扩展性. 但微服务变更频繁、异构融合等特点使得微服务故障频发、其故障传播快且影响大, 同时微服务间复杂的调用依赖关系或逻辑依赖关系又使得其故障难以被及时、准确…...

编程日记 2023/8/8 6:51:47

2023-08-07力扣今日八题

链接&#xff1a; 剑指 Offer 50. 第一个只出现一次的字符 题意&#xff1a; 如题 解&#xff1a; map存下标&#xff0c;由于存在下标0&#xff0c;所以用find&#xff0c;或者记录下标1也可以 实际代码&#xff1a; #include<bits/stdc.h> using namespace std;…...

编程日记 2023/8/8 6:50:45

Segment Anything【论文翻译】

文章目录 论文基础信息如下Abstract1. Introduction2. Segment Anything Task3. Segment Anything Model4. Segment Anything Data Engine5. Segment Anything Dataset6. Segment Anything RAI Analysis7. Zero-Shot Transfer Experiments7.1. Zero-Shot Single Point Valid Ma…...

编程日记 2023/8/8 6:49:44

银河麒麟QT连接DM8数据库

1. 安装达梦8 官网下载, 按照官方文档进行安装即可. 2. 安装unixodbc 1> 下载odbc安装包 unixODBC-2.3.7pre.tar.gz 2> 解压 tar -xvf unixODBC-2.3.7pre.tar.gz3> 编译 ./configure -prefix /usr/local make && make install4> 查找配置 odbcinst -j5…...

编程日记 2023/8/8 6:48:42

并发编程1：线程安全性概述

目录 1、什么是线程安全性&#xff1f; 2、操作的原子性&#xff1a;避免竞态条件 3、锁机制&#xff1a;内置锁和可重入 4、如何用锁来保护状态&#xff1f; 5、同步机制中的活跃性与性能问题 编写线程安全的代码&#xff0c;其核心在于对状态访问操作进行管理&#xff0…...

编程日记 2023/8/8 6:47:41

（论文复现）DeepAnt模型复现及应用

DeepAnt论文如下&#xff0c;其主要是用于时间序列的无监督粗差探测。 其提出的模型架构如下&#xff1a; 该文提出了一个无监督的时间序列粗差探测模型&#xff0c;其主要有预测模块和探测模块组成&#xff0c;其中预测模块的网络结构如下。 预测结构是将时间序列数据组…...

编程日记 2023/8/8 6:46:38

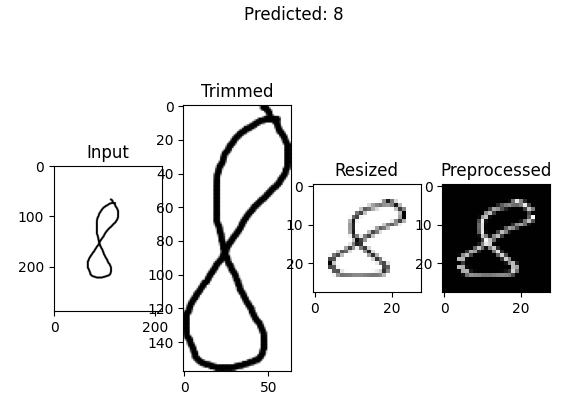
【机器学习】在 MLOps构建项目 （ MLOps2）

My MLOps tutorials: Tutorial 1: A Beginner-Friendly Introduction to MLOps教程 2&#xff1a;使用 MLOps 构建机器学习项目 一、说明 如果你希望将机器学习项目提升到一个新的水平&#xff0c;MLOps 是该过程的重要组成部分。在本文中&#xff0c;我们将以经典手写数字分类…...

编程日记 2023/8/8 6:45:37

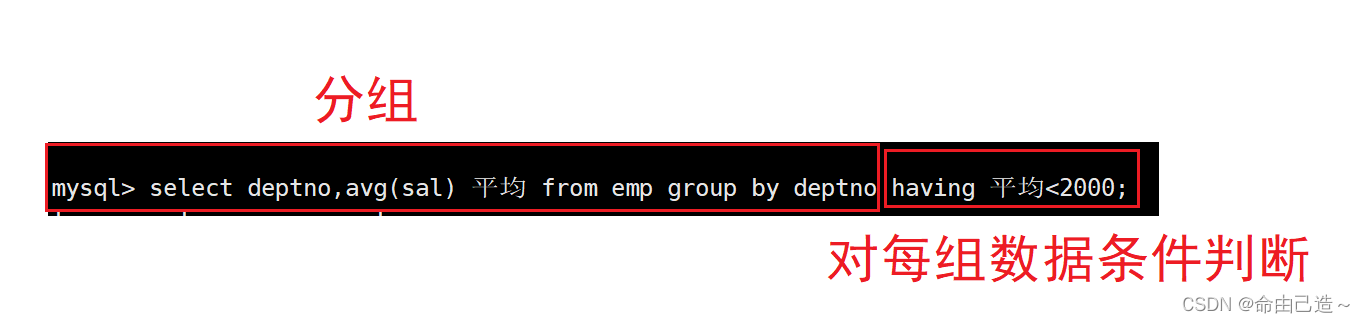
【MySQL】聚合函数与分组查询

文章目录 一、聚合函数1.1 count 返回查询到的数据的数量1.2 sum 返回查询到的数据的总和1.3 avg 返回查询到的数据的平均值1.4 max 返回查询到的数据的最大值1.5 min 返回查询到的数据的最小值 二、分组查询group by2.1 导入雇员信息表2.2 找到最高薪资和员工平均薪资2.3 显示…...

编程日记 2023/8/8 6:44:36

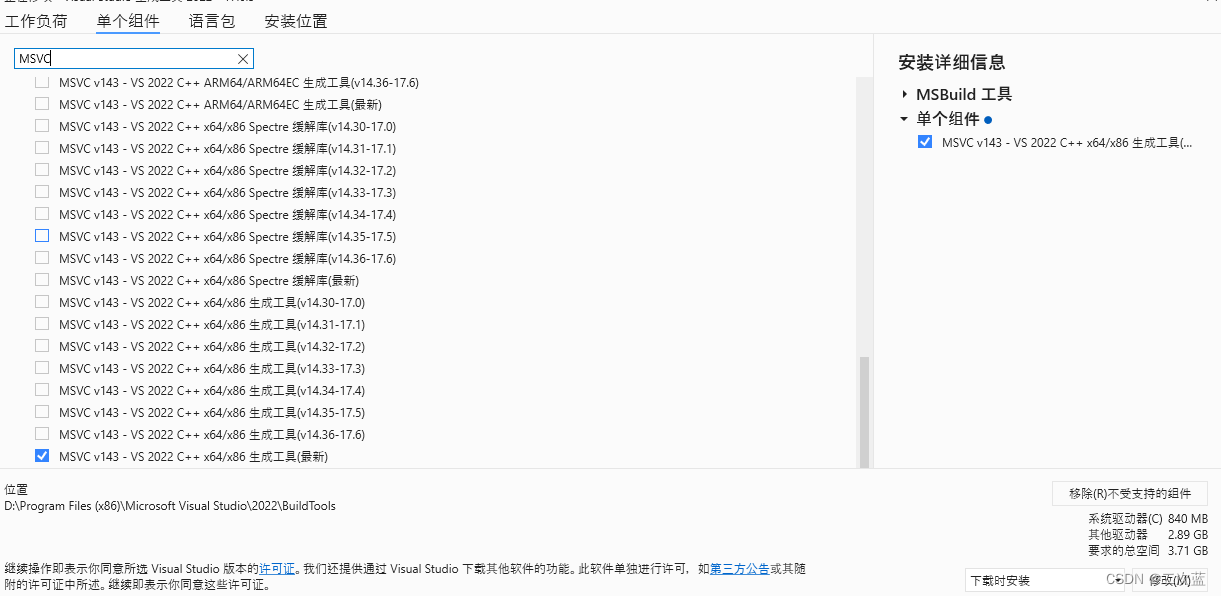
conda 环境 numpy 安装报错需要 Microsoft Visual C++ 14.0

到公司装深度学校环境。项目较旧&#xff0c;安装依赖&#xff0c;一堆报错&#xff08;基于 conda 环境&#xff09;&#xff1a; numpy 安装报需要 C 14.0 No module named numpy.distutils._msvccompiler in numpy.distutils; trying from distutilserror: Microsoft Visu…...

编程日记 2023/8/8 6:43:35

算法工程师-机器学习面试题总结(5)

什么是信息熵&#xff1f; 信息熵是信息理论中用来衡量一个随机变量的不确定度或者信息量的概念。它是在给定一组可能的事件中&#xff0c;对每个事件发生的概率进行加权平均得到的值。 在信息熵的计算中&#xff0c;概率越大的事件所带来的信息量越小&#xff0c;概率越小的事…...

编程日记 2023/8/8 6:42:32

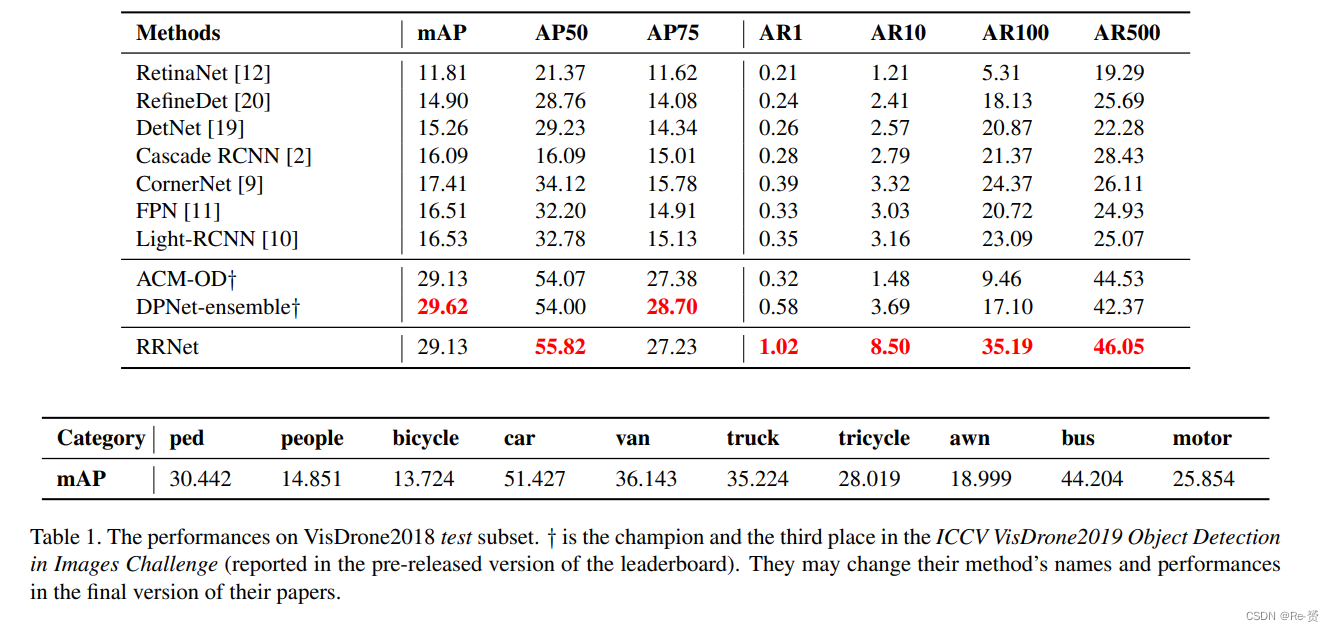
论文阅读 RRNet: A Hybrid Detector for Object Detection in Drone-captured Images

文章目录 RRNet: A Hybrid Detector for Object Detection in Drone-captured ImagesAbstract1. Introduction2. Related work3. AdaResampling4. Re-Regression Net4.1. Coarse detector4.2. Re-Regression 5. Experiments5.1. Data augmentation5.2. Network details5.3. Tra…...

编程日记 2023/8/8 6:41:31

js执行机制

JavaScript 的执行机制是基于单线程的事件循环模型。这意味着 JavaScript 代码会按照顺序一行一行地执行&#xff0c;同时只能执行一个任务。让我们更详细地了解 JavaScript 的执行机制&#xff1a; 调用栈&#xff08;Call Stack&#xff09;&#xff1a; JavaScript 使用调用…...

编程日记 2023/8/8 6:40:28

关于策略模式的注入问题

上面抄别人的 当在实现策略方法时&#xff0c;报null&#xff0c;排查后发现是接口实现有多个&#xff0c;需要添加别名 注入时添加Qeualifier&#xff0c;指定名称&#xff0c;如下图&#xff1b;如图上修改&#xff0c; 测试类中不用new具体行为策略了&#xff0c;注入别名即…...

编程日记 2023/8/8 6:39:27

通用Mapper的四个常见注解

四个常见注解 1、Table 作用&#xff1a;建立实体类和数据库表之间的对应关系。 默认规则&#xff1a;实体类类名首字母小写作为表名&#xff0c;如 Employee -> employee 表 用法&#xff1a;在 Table 注解的 name 属性中指定目标数据库的表名&#xff1b; 案例&#…...

编程日记 2023/8/8 6:38:26

二进制安装K8S(单Master集群架构)

目录 一&#xff1a;操作系统初始化配置 1、项目拓扑图 2、服务器 3、初始化操作 二&#xff1a; 部署 etcd 集群 1、etcd 介绍 2、准备签发证书环境 3、master01 节点上操作 &#xff08;1&#xff09;生成Etcd证书 &#xff08;2&#xff09;创建用于存放 etcd 配置文…...

编程日记 2023/8/8 6:37:25

基于java汽车销售分析与管理系统设计与实现

摘 要 计算机现在已成为人们办公和生活不可或缺的组成部分&#xff0c;在工作范畴计算机成熟运用大大提升了工作人员的工作效率&#xff0c;化繁为简&#xff0c;加速社会经济发展。在生活上&#xff0c;人们可以通过计算机互联网更快的了解到全球时事要闻、听到最新潮流音乐、…...

编程日记 2023/8/8 6:36:24

Glass指纹识别工具，多线程Web指纹识别工具-Chunsou

Glass指纹识别工具&#xff0c;多线程Web指纹识别工具-Chunsou。 Glass指纹识别工具 Glass一款针对资产列表的快速指纹识别工具&#xff0c;通过调用Fofa/ZoomEye/Shodan/360等api接口快速查询资产信息并识别重点资产的指纹&#xff0c;也可针对IP/IP段或资产列表进行快速的指…...

编程日记 2023/8/8 6:35:22

BIO,NIO,AIO总结

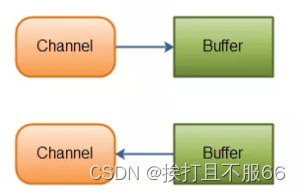
文章目录 1. BIO (Blocking I/O)1.1 传统 BIO1.2 伪异步 IO1.3 代码示例 1.4 总结2. NIO (New I/O)2.1 NIO 简介2.2 NIO的特性/NIO与IO区别1)Non-blocking IO&#xff08;非阻塞IO&#xff09;2)Buffer(缓冲区)3)Channel (通道)4)Selector (选择器) 2.3 NIO 读数据和写数据方式…...

编程日记 2023/8/8 6:34:21

synchronized 学习

学习源&#xff1a; https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖&#xff0c;也要考虑性能问题&#xff08;场景&#xff09; 2.常见面试问题&#xff1a; sync出…...

编程新知 2025/12/14 17:38:17

【位运算】消失的两个数字（hard）

消失的两个数字&#xff08;hard&#xff09; 题⽬描述&#xff1a;解法&#xff08;位运算&#xff09;&#xff1a;Java 算法代码&#xff1a;更简便代码 题⽬链接&#xff1a;⾯试题 17.19. 消失的两个数字 题⽬描述&#xff1a; 给定⼀个数组&#xff0c;包含从 1 到 N 所有…...

编程新知 2025/11/15 16:18:24

CentOS下的分布式内存计算Spark环境部署

一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架&#xff0c;相比 MapReduce 具有以下核心优势&#xff1a; 内存计算&#xff1a;数据可常驻内存&#xff0c;迭代计算性能提升 10-100 倍&#xff08;文档段落&#xff1a;3-79…...

编程新知 2026/2/5 1:30:05

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践

一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架&#xff0c;支持"一次开发&#xff0c;多端部署"&#xff0c;可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务&#xff0c;为旅游应用带来&#xf…...

编程新知 2026/2/5 20:33:43

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现，论文初版实现

摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序&#xff0c;以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务&#xff0c;提供稳定高效的数据处理与业务逻辑支持&#xff1b;利用 uniapp 实现跨平台前…...

编程新知 2026/1/31 10:55:22

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错

出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上&#xff0c;所以报错&#xff0c;到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本&#xff0c;cu、torch、cp 的版本一定要对…...

编程新知 2025/11/3 2:11:24

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战

“&#x1f916;手搓TuyaAI语音指令 &#x1f60d;秒变表情包大师&#xff0c;让萌系Otto机器人&#x1f525;玩出智能新花样&#xff01;开整&#xff01;” &#x1f916; Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制&#xff08;TuyaAI…...

编程新知 2026/1/30 16:09:53

vue3+vite项目中使用.env文件环境变量方法

vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量&#xff0c;这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

编程新知 2026/1/26 19:12:01

云原生玩法三问：构建自定义开发环境

云原生玩法三问&#xff1a;构建自定义开发环境 引言 临时运维一个古董项目&#xff0c;无文档&#xff0c;无环境&#xff0c;无交接人&#xff0c;俗称三无。 运行设备的环境老&#xff0c;本地环境版本高&#xff0c;ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

编程新知 2026/2/2 9:25:26

springboot整合VUE之在线教育管理系统简介

可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生&#xff0c;小白用户&#xff0c;想学习知识的 有点基础&#xff0c;想要通过项…...

编程新知 2026/1/26 9:30:45