全面讲解最小二乘法
常见的最小二乘法我们就不多说了,下面主要介绍一下最小二乘法的一些先进方法。
-
正则化的最小二乘法
在使用常见的最小二乘法进行回归分析时,常常会遇到过拟合的问题,也就是在训练数据集上表现的很好,但是在测试数据集上表现的很差。这时候就需要将最小二乘法中引入一个正则化项。常见的正则化有两种。
L2正则化(Ridge回归):
L1正则化(Lasso回归):
从概率的角度解释正则化:正则化相当于参数W的先验分布。如果该分布是
的高斯分布,就是L2正则化;如果该分布是
的拉普拉斯分布,则是L1正则化。通过加入正则化来限制参数空间,控制模型的复杂度,从而防止过拟合。
-
阻尼最小二乘法(Levenberg–Marquardt algorithm,LMA)
我们常用的最小二乘法是拟合线性方程组,但是对于非线性的函数,我们就要用阻尼最小二乘法,本质上是一个迭代求解的过程,基本思想是利用泰勒展开把非线性函数线性化。
设方程,其中x是变量,c是要拟合的参数。我们要找到一组c使得:
将函数泰勒展开,只保留一阶项,可以得到:
其中是雅克比矩阵:
从而有,从而可以解出
,不断迭代更新
,直到
。
相关文章:
全面讲解最小二乘法
常见的最小二乘法我们就不多说了,下面主要介绍一下最小二乘法的一些先进方法。 正则化的最小二乘法 在使用常见的最小二乘法进行回归分析时,常常会遇到过拟合的问题,也就是在训练数据集上表现的很好,但是在测试数据集上表现的很…...
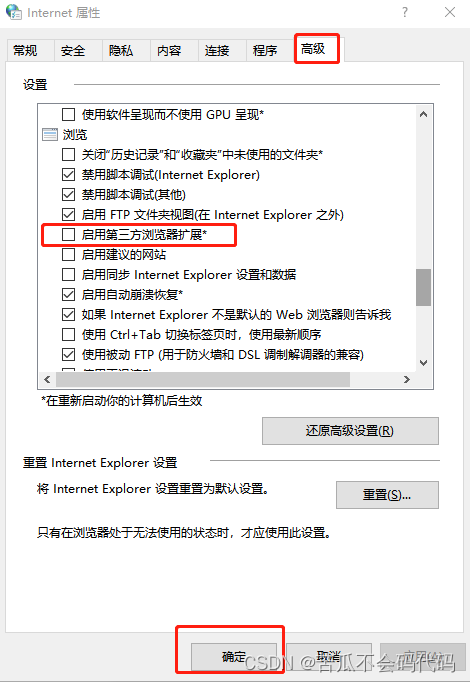
【阻止IE强制跳转到Edge浏览器】
由于微软开始限制用户使用Internet Explorer浏览网站,IE浏览器打开一些网页时会自动跳转到新版Edge浏览器,那应该怎么禁止跳转呢? 1、点击电脑左下角的“搜索框”或者按一下windows键。 2、输入“internet”,点击【Internet选项…...
)
C++/Linux项目——日志系统(简介)
一,日志系统的目的 1.⽣产环境的产品为了保证其稳定性及安全性是不允许开发⼈员附加调试器去排查问题, 可以借助⽇志系统来打印⼀些⽇志帮助开发⼈员解决问题 2.上线客⼾端的产品出现bug⽆法复现并解决, 可以借助⽇志系统打印⽇志并上传到服…...

【Redis面试题整理一】
一、Redis定义 Redis 是一种基于内存的数据库,对数据的读写操作都是在内存中完成,读写速度非常快,被广泛应用于缓存方向。并且,Redis 存储的是 KV 键值对数据。 二、Redis为什么不存在并发竞争 对数据类型的操作都是原子性的&a…...

前端权限验证之自定义指令v-permission
自定义指令 在前端处理按钮权限详细代码 在前端处理按钮权限 使用vue自定义指令来v-permission 来控制按钮 详细代码 //index.js文件 import permission from ./permissionconst install function(Vue) {Vue.directive(permission, permission) }if (window.Vue) {window[p…...
)
c++使用条件变量实现生产消费问题(跨平台)
1. 生产者线程 思路:队列满了的情况下, 触发条件变量wait, 等待消费线程消费后唤醒继续生产. void ProducerThreadFunc() {while(1) { while(/* 容器已满 */) { /* 线程等待, 直到消费者消费后唤醒继续执行 */ }/* 生产动作 */ } }2. 消…...
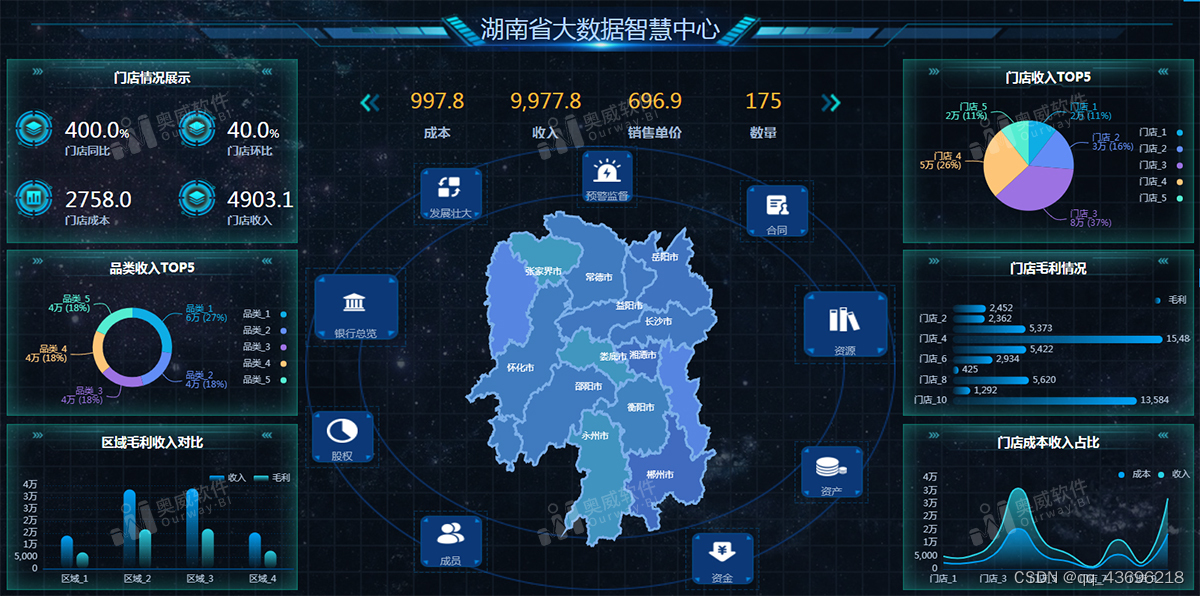
怎么快速搭建BI?奥威BI系统做出了表率
搭建BI系统有两大关键,分别是环境搭建和数仓建设。这两点不管是哪一个都相当地费时费力,那要怎么才能快速搭建BI平台,顺利实现全企业数字化运营决策?奥威BI系统方案,你值得拥有! 奥威BI系统方案࿰…...
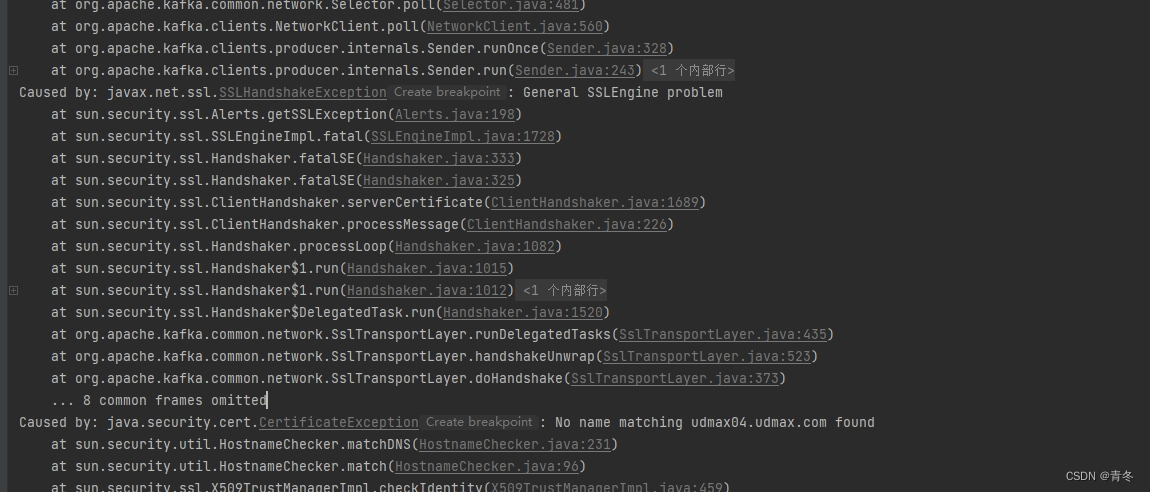
Kafka3.4 SASL/kerberos/ACL 证以及 SSL 加密连接
Kafka3.4 SASL/kerberos ACL 证以及 SSL 加密连接 序 前面我们使用 kafka3.3.1 on zookeeper 的模式进行多网段监听的 kafka 集群,顺便搭建起 kafkaui 后发现一些问题,我们 kafka 集群没有连接认证,万一谁知道了我们的 kafka 连接地址&…...
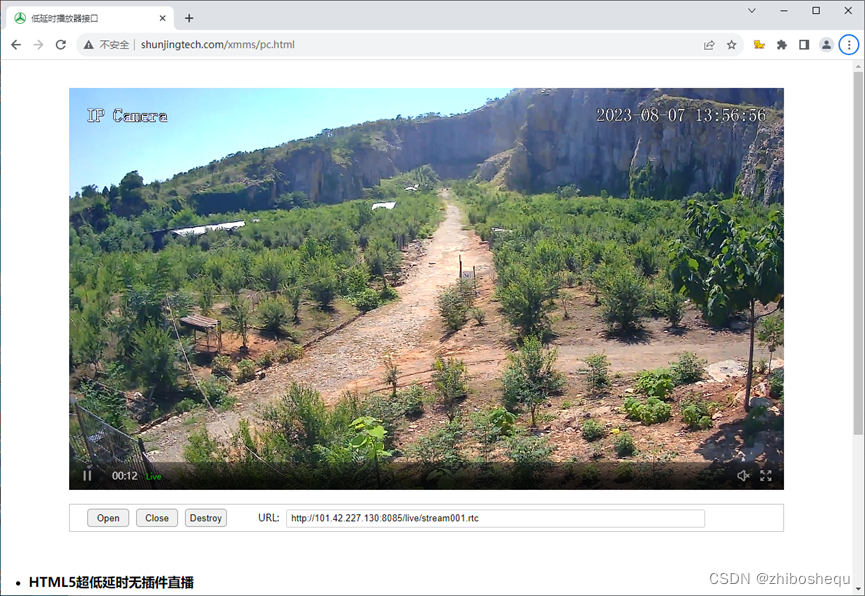
UE中低延时播放RTSP监控视频解决方案
第1章 方案简介 1.1 行业痛点 在各种智慧城市、智慧社区、智慧水利、智慧矿山等数字孪生项目中,经常使用通UE来开发三维可视化场景。在这些场景中通常都需要把现场的各种监控视频在UE的可视化场景中接入,主要包含海康威视、大华、宇视、华为等众多监控…...
iOS - 开发者账号续订会员资格更换订阅的账号
文章目录 前言开发环境续订会员资格转让账户持有人验证身份1. 实名认证2. 联系信息 更换订阅的账号最后 前言 公司有一个开发者账号快到期了需要续订会员资格,刚注册时是用我自己的个人账号完成的订阅购买。现在想来有点不妥,于是尝试更换用于订阅的账号…...

大数据课程F3——HIve的基本操作
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握HIve的基本SQL语句和注意问题; ⚪ 掌握HIve的表结构; ⚪ 掌握HIve的数据类型; ⚪ 掌握HIve的基础函数和窗口函数; 一、基本SQL 1. SQL的执行方式 1. 通过hive -e的方式来执行指…...

top解析
top - 13:52:26 up 26 days, 20:56, 2 users, load average: 0.00, 0.01, 0.05 当前时间 系统运行时间,格式为时:分 当前登陆用户数2 系统负载,即任务队列的平均长度。三个数值分别为1分钟,5分钟,15分钟前到现在的平均…...

如何让子组件,router-view,呈现左右分布格局
1.用浮动进行浮动布局,定义一个大盒子,把浮动的样式写在公共样式里(这里在main.js里定义一下全局布局)。 2、能够在右边显示了...
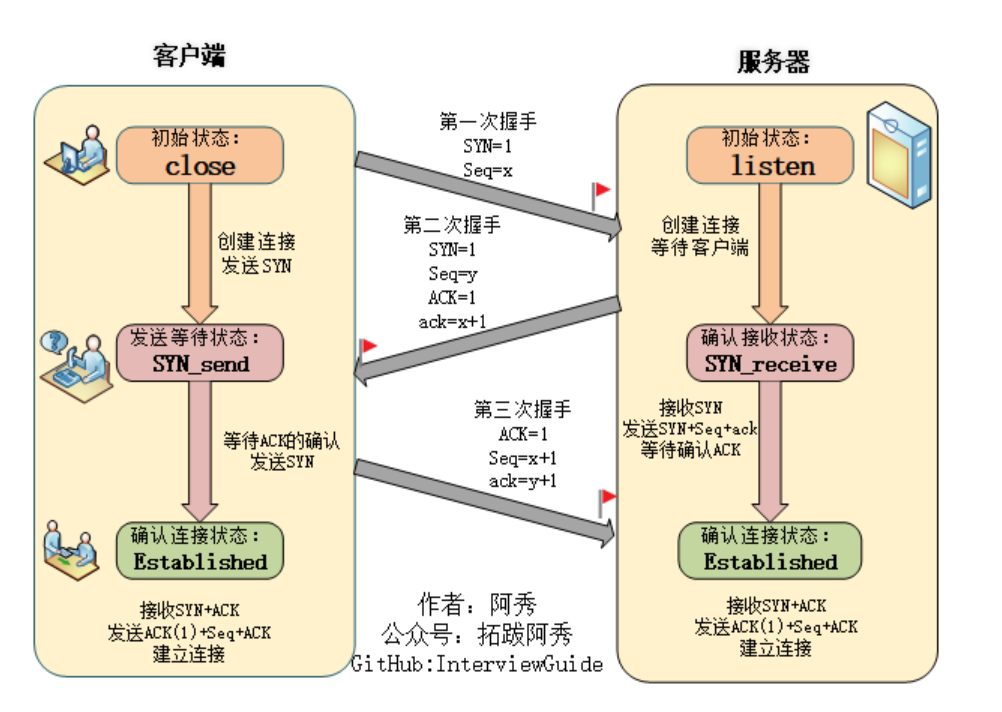
计算机网络—TCP和UDP、输入url之后显示主页过程、TCP三次握手和四次挥手
TCP基本认识 TCP是面向连接的、可靠的,基于字节流的传输层通信协议。 图片来源小林coding 序号:传输方向上字节流的字节编号。初始时序号会被设置一个随机的初始值(ISN),之后每次发送数据时,序号值 ISN…...
使用反汇编工具IDA查看发生异常的汇编代码的上下文去辅助分析C++软件异常
目录 1、概述 2、如何使用IDA打开并查看二进制文件的汇编代码 3、在IDA中找到发生崩溃的那条汇编指令的位置 3.1、如何在IDA中找到发生异常的那条汇编指令 3.2、示例 4、阅读汇编代码上下文需要掌握一定的基础汇编知识 5、最后 VC常用功能开发汇总(专栏文章列…...
怎么合并多个视频?简单视频合并方法分享
合并多个视频可以将它们组合成一个更长的视频,这对于需要播放多个短视频的情况非常有用。此外,合并视频还可以使视频编辑过程更加高效,因为不必将多个独立的视频文件分别处理。最后,合并视频可以减少文件数量,从而使整…...
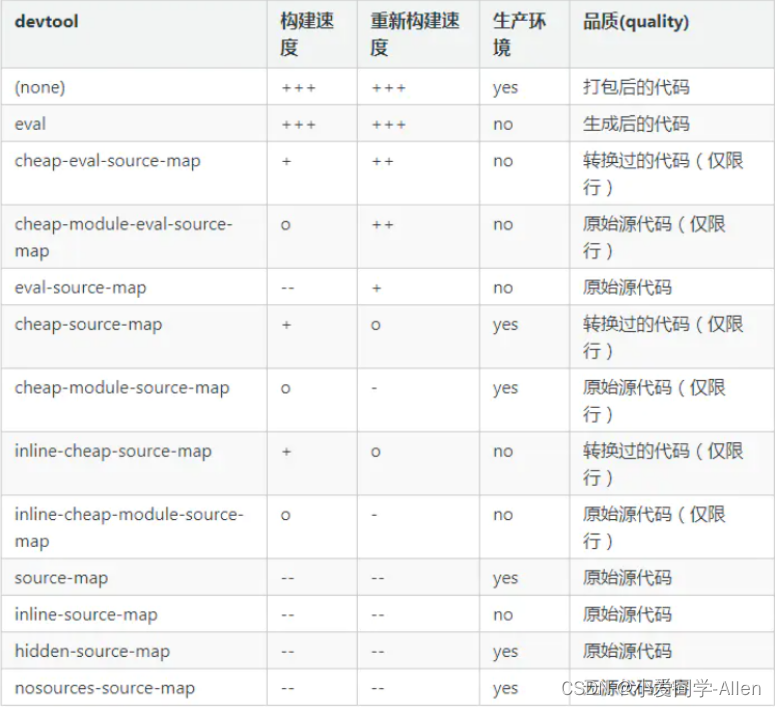
webpack基础知识九:如何提高webpack的构建速度?
一、背景 随着我们的项目涉及到页面越来越多,功能和业务代码也会随着越多,相应的 webpack 的构建时间也会越来越久 构建时间与我们日常开发效率密切相关,当我们本地开发启动 devServer 或者 build 的时候,如果时间过长ÿ…...

批量改名字序号和前缀
echo off setlocal enabledelayedexpansion set count10 for /f %%i in (dir /b *.jpg,*.png,*.bmp,*.jpeg,*.gif) do ( set /a count1 echo %%i 前缀_!count! rename %%i 前缀_!count!.png ) REM …...
基于Spring Boot的医院预约挂号网站设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于Spring Boot的医院预约挂号网站设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:Java spring…...

Linux命令200例:join将两个文件按照指定的键连接起来分析
🏆作者简介,黑夜开发者,全栈领域新星创作者✌。CSDN专家博主,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师,项目技术负责人。 &…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

02-性能方案设计
需求分析与测试设计 根据具体的性能测试需求,确定测试类型,以及压测的模块(web/mysql/redis/系统整体)前期要与相关人员充分沟通,初步确定压测方案及具体的性能指标QA完成性能测试设计后,需产出测试方案文档发送邮件到项目组&…...
无头浏览器技术:Python爬虫如何精准模拟搜索点击
1. 无头浏览器技术概述 1.1 什么是无头浏览器? 无头浏览器是一种没有图形用户界面(GUI)的浏览器,它通过程序控制浏览器内核(如Chromium、Firefox)执行页面加载、JavaScript渲染、表单提交等操作。由于不渲…...
