数据结构中一些零碎且易忘的知识点
树
- 并查集:
- 并查集的应用:
- 判断连通性、判环
- Kruskal算法=排序+并查集
- 并查集的存储方式
- 逻辑:双亲表示法的树
- 存储:数组
- 并查集的时间复杂度(m为并查集长度)
- find:优化前为 O ( m ) O(m) O(m);优化后为 O ( l o g 2 n ) O(log_{2}n) O(log2n)
- union: O ( 1 ) O(1) O(1)
- 总复杂度:优化前 O ( m 2 ) O(m^2) O(m2);优化后 O ( m ) O(m) O(m)
- 并查集的应用:
- 树、森林、二叉树遍历序列的关系
树 森林 二叉树 先根遍历 先序遍历 先序遍历 后根遍历 中序遍历 中序遍历 关于森林的中序遍历/后序遍历叫法问题:二者指森林的同一种遍历方法,都是先遍历第一棵树的子节点,然后是第一棵树的根节点,然后是第二棵树… 之所以称为中序遍历,是因为要先处理完一棵树再处理另一棵树。
图
- DFS与BFS算法的应用:
- DFS:
- 判断图的(强)连通性
- 无向图的连通性:若从任意一个节点出发,仅需一次DFS就可以访问图中所有节点,则该无向图就是连通的
- 有向图的强连通性:从任意一个节点v出发DFS,若可以遍历该有向图的所有节点,则此时将该有向图的所有边反向,再次从节点v出发进行DFS,若能够再次遍历该有向图的所有节点,则表示该有向图是强连通图
- 判断图中是否有环(回路)
- 欧拉回路求解:若一条路径能不重复的包含图中所有边,则称该路径为欧拉路径。若一条回路(从一个节点出发又能回到该节点的路径)是欧拉路径,则称为欧拉回路。DFS可以判断图中是否存在欧拉回路
- 迷宫
- 判断二分图
- 判断图的(强)连通性
- BFS:
- 求解单源最短路径问题(只适用于无权图)
- 迷宫
- 判断二分图
- DFS:
- 最短路径
- 有无环(回路)对Dijkstra算法并无影响,但Dijkstra算法不能求解存在负权值边的图;Floyd算法可以求带有负权值边的图,但图中不能存在负权回路(因为带有负权回路的图没有最短路径)
- Dijkstra算法是解决单源最短路径类问题,floyd算法是解决多源最短路径(指图中任意两个顶点之间的最短路径)类问题
- Dijkstra算法属于贪心算法,floyd算法属于动态规划算法
- 判断有向图是否有环(回路)的几种方法:
- 深度优先遍历:若在遍历过程中遇到要访问的节点已在栈中就是有环
- 拓扑排序:找不到拓扑序列必定有环
- 拓扑排序
- 在拓扑排序算法中,为暂存入度为零的顶点可以使用栈,也可以使用队列。(因为只要入了栈/队列,就都是入度为零的,从哪个入度为零的先开始都无所谓)
- 采用深度优先遍历也可实现拓扑排序
相关文章:

数据结构中一些零碎且易忘的知识点
树 并查集: 并查集的应用: 判断连通性、判环Kruskal算法排序并查集 并查集的存储方式 逻辑:双亲表示法的树存储:数组 并查集的时间复杂度(m为并查集长度) find:优化前为 O ( m ) O(m) O(m)&…...
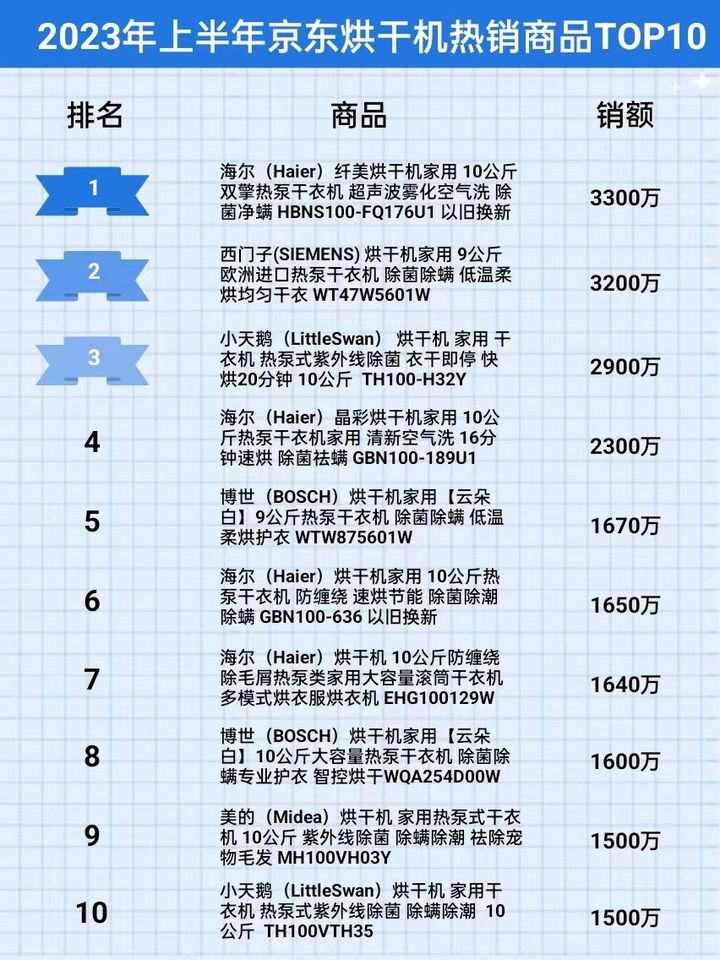
2023上半年京东烘干机行业品牌销售排行榜(京东商品数据)
随着人们消费水平的提高,追求健康品质消费的用户越来越多,这样的消费升级为市场的发展带来很大的动力。同时,随着洗衣机市场趋向饱和,增长趋于平缓,更新换代和结构升级成为行业的主旋律。 在这一市场背景下࿰…...

ADS版图画封装学习笔记
ADS版图画封装 因为晶体管ATF54143在ADS中是没有封装的,所以要在ADS中画ATF54143的封装,操作步骤如下: 在ADS中新建layout,命名为ATF54143_layout, 根据datasheet知道封装的大小,进行绘制 在layout的con…...
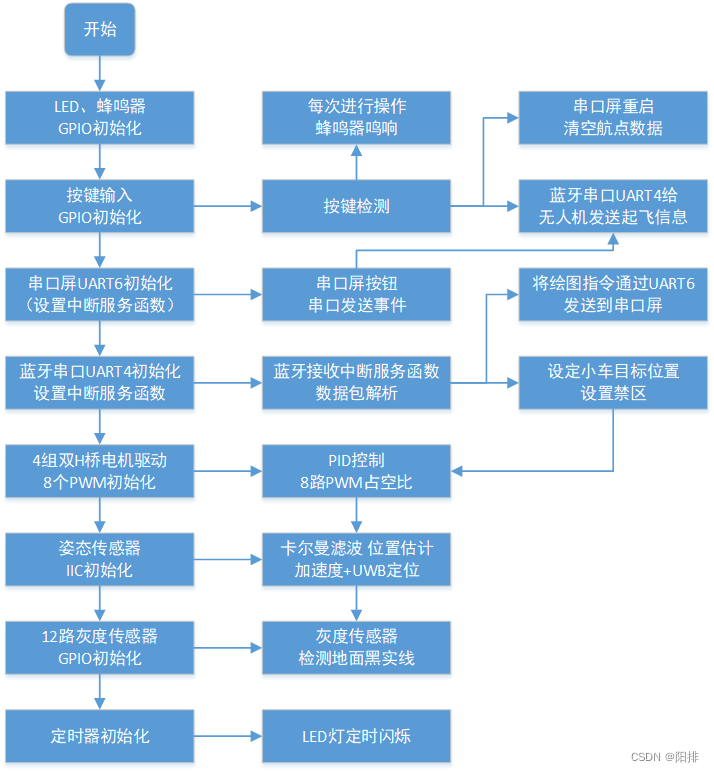
空地协同智能消防系统——无人机、小车协同
1 题目 1.1 任务 设计一个由四旋翼无人机及消防车构成的空地协同智能消防系统。无人机上安装垂直向下的激光笔,用于指示巡逻航迹。巡防区域为40dm48dm。无人机巡逻时可覆盖地面8dm宽度区域。以缩短完成全覆盖巡逻时间为原则,无人机按照规划航线巡逻。发…...

篇二十二:解释器模式:处理语言语法
篇二十二:"解释器模式:处理语言语法" 开始本篇文章之前先推荐一个好用的学习工具,AIRIght,借助于AI助手工具,学习事半功倍。欢迎访问:http://airight.fun/。 另外有2本不错的关于设计模式的资料…...
【LeetCode 75】第二十一题(1207)独一无二的出现次数
目录 题目: 示例: 分析: 代码运行结果: 题目: 示例: 分析: 用两个unordered_map来分别存放每个数字的出现次数和出现的次数这个数,有点绕,比如说有给的数组有两个1,那么第一个map存放的是(1,2),表示1这个数子出现了两次,而第二个map存放的是(2,true),表示有出现次数为2的数…...

node中使用express+mongodb实现分页查询
文章目录 引言一、分页案例二、查询方法扩展介绍1. find()2. limit()3. skip()4. populate() 总结 引言 在Web应用程序开发中,分页查询是必不可少的功能之一。Node.js提供了许多优秀的工具和框架来实现分页查询,其中最流行的框架之一就是Express。同时&…...

信创优选,国产开源。Solon v2.4.2 发布
Solon 是什么开源项目? 一个,Java 新的生态型应用开发框架。它从零开始构建,有自己的标准规范与开放生态(历时五年,已有全球第二级别的生态规模)。与其他框架相比,它解决了两个重要的痛点&…...

Java HTTP client常见库
前言 每种编程语言里最常用的库恐怕是Http请求库了,如python里的requests包,nodejs里的request模块。 在Java世界里,也是百花齐放,山头林立。常用的有: HttpURLConnection: 最早的JDK提供的类Java 11提供的HttpClien…...

【Java基础教程】(四十四)IO篇 · 上:File类、字节流与字符流,分析字节输出流、字节输入流、字符输出流和字符输入流的区别~
Java基础教程之IO操作 上 🔹本节学习目标1️⃣ 文件操作类:File2️⃣ 字节流与字符流2.1 字节输出流:OutputStream2.2 字节输入流:InputStream2.3 字符输出流:Writer2.4 字符输入流:Reader2.5 字节流与字符…...

电商数据获取:网络爬虫还是付费数据接口?
随着电商行业的迅速发展,对电商数据的需求也越来越大。在获取电商数据时,常常面临一个选择:是自己编写网络爬虫进行数据爬取,还是使用现有的付费数据接口呢?本文将从成本、可靠性、数据质量等多个角度进行分析…...

树形结构——二叉树类型
本文主要介绍树形结构中的二叉树类型,包括二叉树、平衡二叉树、二叉查找树和完全二叉树; 1.二叉树 二叉树是一种树形结构,其中每个节点最多有两个子节点,通常称为左子节点和右子节点。二叉树具有以下特点: 每个节点…...

JavaScript对象的方法与原型链
在JavaScript中,对象是一种非常重要的数据类型,它允许我们将多个属性和方法组织在一起。对象的方法和原型链是理解JavaScript中面向对象编程的关键概念。本文将详细讲解对象的方法和原型链,用通俗易懂的方式帮助你深入理解这些概念。 1. 对象…...

Oracle入门初探---第一章 批量创建表、索引并插入测试数据
Oracle系列文章目录 第一章 批量创建表并插入测试数据 文章目录 Oracle系列文章目录前言一、创建表和索引二、向表中加入数据总结 前言 使用数据库,首先要向数据库中加入大量数据,本篇文章提供了一些测试数据 一、创建表和索引 -- 创建数据库和索引 -…...
全面讲解最小二乘法
常见的最小二乘法我们就不多说了,下面主要介绍一下最小二乘法的一些先进方法。 正则化的最小二乘法 在使用常见的最小二乘法进行回归分析时,常常会遇到过拟合的问题,也就是在训练数据集上表现的很好,但是在测试数据集上表现的很…...
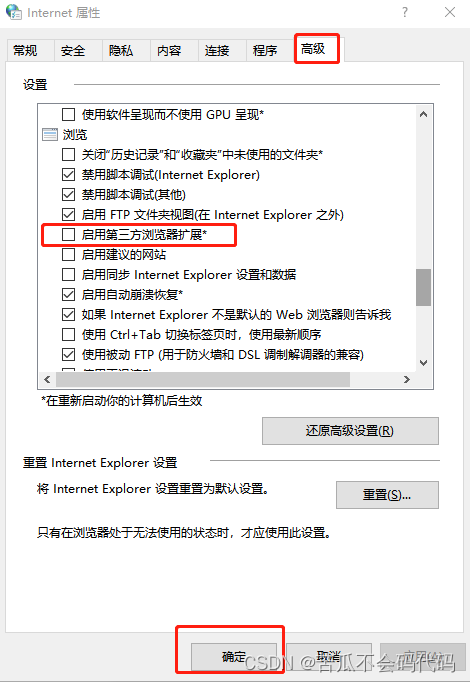
【阻止IE强制跳转到Edge浏览器】
由于微软开始限制用户使用Internet Explorer浏览网站,IE浏览器打开一些网页时会自动跳转到新版Edge浏览器,那应该怎么禁止跳转呢? 1、点击电脑左下角的“搜索框”或者按一下windows键。 2、输入“internet”,点击【Internet选项…...
)
C++/Linux项目——日志系统(简介)
一,日志系统的目的 1.⽣产环境的产品为了保证其稳定性及安全性是不允许开发⼈员附加调试器去排查问题, 可以借助⽇志系统来打印⼀些⽇志帮助开发⼈员解决问题 2.上线客⼾端的产品出现bug⽆法复现并解决, 可以借助⽇志系统打印⽇志并上传到服…...

【Redis面试题整理一】
一、Redis定义 Redis 是一种基于内存的数据库,对数据的读写操作都是在内存中完成,读写速度非常快,被广泛应用于缓存方向。并且,Redis 存储的是 KV 键值对数据。 二、Redis为什么不存在并发竞争 对数据类型的操作都是原子性的&a…...

前端权限验证之自定义指令v-permission
自定义指令 在前端处理按钮权限详细代码 在前端处理按钮权限 使用vue自定义指令来v-permission 来控制按钮 详细代码 //index.js文件 import permission from ./permissionconst install function(Vue) {Vue.directive(permission, permission) }if (window.Vue) {window[p…...
)
c++使用条件变量实现生产消费问题(跨平台)
1. 生产者线程 思路:队列满了的情况下, 触发条件变量wait, 等待消费线程消费后唤醒继续生产. void ProducerThreadFunc() {while(1) { while(/* 容器已满 */) { /* 线程等待, 直到消费者消费后唤醒继续执行 */ }/* 生产动作 */ } }2. 消…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
