树形结构——二叉树类型
本文主要介绍树形结构中的二叉树类型,包括二叉树、平衡二叉树、二叉查找树和完全二叉树;
1.二叉树
二叉树是一种树形结构,其中每个节点最多有两个子节点,通常称为左子节点和右子节点。二叉树具有以下特点:
- 每个节点最多有两个子节点,分别为左子节点和右子节点。
- 左子节点的值小于或等于当前节点的值,而右子节点的值大于当前节点的值。这个特性使得二叉树在查找和排序方面有很大的应用价值。
- 二叉树可以为空树,此时没有节点。
二叉树可以用递归或迭代方式来遍历。常见的二叉树遍历方法包括:
- 前序遍历(Preorder Traversal):先访问根节点,再依次访问左子树和右子树。
- 中序遍历(Inorder Traversal):先访问左子树,再访问根节点,最后访问右子树。中序遍历的结果是有序的。
- 后序遍历(Postorder Traversal):先访问左子树,再访问右子树,最后访问根节点。
- 层序遍历(Level Order Traversal):按层级顺序从上到下逐层遍历,即先访问根节点,然后访问第二层的所有节点,接着访问第三层的所有节点,以此类推。
1.1 二叉树的创建
创建一个二叉树的类型
class TreeNode
{
public:int data;TreeNode* left;TreeNode* right;TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};class BinaryTree
{
public:BinaryTree() : root(nullptr) {}~BinaryTree(){}// 创建二叉树void createTree(int val) { root = createNode(val); }// 创建新节点TreeNode* createNode(int val) {if (val == -1) {return nullptr;} else {return new TreeNode(val);}}
private:TreeNode* root;
};
1.2 二叉树元素的插入
通过递归插入新的元素,这里需要区分根节点是否空;
// 插入节点void insert(int val) {if (root == nullptr) {root = new TreeNode(val);return;}insertNode(root, val);}// 递归插入节点void insertNode(TreeNode* node, int val) {if (val <= node->data) {if (node->left == nullptr) {node->left = new TreeNode(val);} else {insertNode(node->left, val);}} else {if (node->right == nullptr) {node->right = new TreeNode(val);} else {insertNode(node->right, val);}}}
1.3 二叉树的删除
二叉树的删除使用递归的思想
// 删除二叉树void deleteTree(TreeNode* node) {if (node == nullptr) {return;}deleteTree(node->left);deleteTree(node->right);delete node;}
1.4 二叉树的遍历
二叉树的遍历分为前序遍历,中序遍历和后序遍历
//二叉树的遍历——先序(先访问根节点)void preorderTraversal(TreeNode* root) {if (root == nullptr) {return;}// 访问根节点std::cout << root->data << " ";// 先序遍历左子树preorderTraversal(root->left);// 先序遍历右子树preorderTraversal(root->right);}//二叉树的遍历——中序(先访问左子树)void inorderTraversal(TreeNode* root) {if (root == nullptr) {return;}// 中序遍历左子树inorderTraversal(root->left);// 访问根节点std::cout << root->data << " ";// 中序遍历右子树inorderTraversal(root->right);}//二叉树的遍历——后序(先访问右子树)void postorderTraversal(TreeNode* root) {if (root == nullptr) {return;}// 后序遍历左子树postorderTraversal(root->left);// 后序遍历右子树postorderTraversal(root->right);// 访问根节点std::cout << root->data << " ";}
1.5 二叉树的判空
// 判断二叉树是否为空bool isEmpty() {return root == nullptr;}
1.6 二叉树的大小计算和深度计算
二叉树的大小计算指的是树形结构中有多少个元素;
二叉树的深度计算指的是树形结构中有多少层;
// 获取二叉树的深度int getTreeDepth(TreeNode* root) {if (root == nullptr) {return 0;}int leftDepth = getTreeDepth(root->left);int rightDepth = getTreeDepth(root->right);return std::max(leftDepth, rightDepth) + 1;}int getTreeSize(TreeNode* root){int re= 0;//tree为空的时候if(root == nullptr){return re;}int left_size = getTreeSize(root->left);int right_size = getTreeSize(root->right);re = left_size + right_size + 1;return re;}
1.7 二叉树的查找
查找某一个元素是否在二叉树中,如果存在则返回true,不存在则返回false
// 查询节点值是否存在于二叉树中bool search(int val) {return searchNode(root, val);}// 递归查询节点值是否存在于二叉树中bool searchNode(TreeNode* node, int val) {if (node == nullptr) {return false;}if (node->data == val) {return true;}return searchNode(node->left, val) || searchNode(node->right, val);}TreeNode* getRootValue(){return root;}
二叉树的使用
2.平衡二叉树(AVL树)
平衡二叉树是一种特殊的二叉树,它的左子树和右子树的高度差不超过1,并且左子树和右子树也都是平衡二叉树。平衡二叉树的设计目的是为了保持树的平衡,提高查找、插入和删除操作的效率,避免出现退化成链表的情况。实现一个平衡二叉树可以使用各种方法,最常用的是AVL树和红黑树。这些方法都通过旋转、重新平衡等操作来保持树的平衡性。在插入或删除节点时,需要根据树的平衡性进行相应调整,以保证树仍然是平衡的。平衡二叉树的平衡性可以确保树上的操作的时间复杂度为O(log n),提供了高效的数据访问和操作能力。
平衡二叉树与二叉树相比,在元素插入的时候需要根据平衡因子,进行左旋操作或者右旋操作;
2.1 平衡二叉树的结构
class TreeNode
{
public:int val;int height;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), height(1), left(nullptr), right(nullptr) {}
};
2.3 获取平衡因子
这里的平衡因子指的是左子树和右子树的高度差值
// 获取节点的平衡因子int getBalanceFactor(TreeNode* node) {if (node == nullptr) {return 0;}return getHeight(node->left) - getHeight(node->right);}// 获取节点的高度int getHeight(TreeNode* node) {if (node == nullptr) {return 0;}return node->height;}// 更新节点的高度void updateHeight(TreeNode* node) {node->height = std::max(getHeight(node->left), getHeight(node->right)) + 1;}
2.2 左旋操作和右旋操作
左旋操作和右旋操作是为了调整树形结构的高度;
// 右旋操作,根节点TreeNode* rotateRight(TreeNode* y) {TreeNode* x = y->left;TreeNode* T2 = x->right;x->right = y;y->left = T2;updateHeight(y);updateHeight(x);return x;}// 左旋操作,根节点TreeNode* rotateLeft(TreeNode* x) {TreeNode* y = x->right;TreeNode* T2 = y->left;y->left = x;x->right = T2;updateHeight(x);updateHeight(y);return y;}
2.3 元素的插入
在每一个元素插入的时候,都需要根据平衡因子来判断是否需要进行左旋和右旋的操作;
void insert(int val){if (root == nullptr) {root = new TreeNode(val);return;}root = insertNode(root, val); }// 插入节点TreeNode* insertNode(TreeNode* node, int val) { if (val < node->val) {if(node->left == nullptr ) {node->left = new TreeNode(val);}else{node->left = insertNode(node->left, val);} } else if (val > node->val) {if(node->right == nullptr){node->right = new TreeNode(val);}else{node->right = insertNode(node->right, val);}} else {std::cout<<"same data!"<<std::endl; return node;}updateHeight(node);int balanceFactor = getBalanceFactor(node); if(node->left != nullptr){// Left-Left caseif (balanceFactor > 1 && val < node->left->val) {return rotateRight(node);}// Left-Right caseif (balanceFactor > 1 && val > node->left->val) {node->left = rotateLeft(node->left);return rotateRight(node);} }if(node->right != nullptr){ // Right-Right caseif (balanceFactor < -1 && val > node->right->val) {return rotateLeft(node);}// Right-Left caseif (balanceFactor < -1 && val < node->right->val) {node->right = rotateRight(node->right);return rotateLeft(node);} }return node;}
3.二叉查找树(BST)
二叉查找树(Binary Search Tree,BST)是一种特殊的二叉树,它满足以下条件:
- 对于树中的每个节点,其左子树中的所有节点的值都小于该节点的值。
- 对于树中的每个节点,其右子树中的所有节点的值都大于该节点的值。
- 对于树中的每个节点,其左子树和右子树都是二叉查找树。
因此,二叉查找树具有以下特点:
- 左子节点的值小于父节点的值,右子节点的值大于父节点的值。
- 中序遍历二叉查找树得到的值序列是递增有序的。
- 可以快速插入、删除和查找节点。
4.完全二叉树
完全二叉树(Complete Binary Tree)是一种特殊类型的二叉树,在完全二叉树中,除了最后一层,其他层的节点都是满的,且最后一层的节点尽可能地靠左排列。
具体来说,完全二叉树的定义如下:
- 如果一个二叉树的高度为h(h >= 0),并且它的节点从第 1 层到第 h-1 层都是满的,第 h 层的节点都连续地排列在最左边若干位置上,那么这棵二叉树就是完全二叉树。
- 如果一个完全二叉树的最后一层有缺失节点,则缺失节点只能集中在层末尾的若干位置上,并且缺失的节点都是从左到右依次缺失的(即不会出现在中间位置缺失)。
完全二叉树主要涉及到元素的插入
void insert(int value) {Node* newNode = new Node(value);// root是根节点if (root == nullptr) {root = newNode;return;}std::queue<Node*> q;q.push(root);while (!q.empty()) {Node* front = q.front();q.pop(); //删除队首元素if (front->left == nullptr) {front->left = newNode;return;} else if (front->right == nullptr) {front->right = newNode;return;}q.push(front->left); q.push(front->right);}
}
相关文章:

树形结构——二叉树类型
本文主要介绍树形结构中的二叉树类型,包括二叉树、平衡二叉树、二叉查找树和完全二叉树; 1.二叉树 二叉树是一种树形结构,其中每个节点最多有两个子节点,通常称为左子节点和右子节点。二叉树具有以下特点: 每个节点…...

JavaScript对象的方法与原型链
在JavaScript中,对象是一种非常重要的数据类型,它允许我们将多个属性和方法组织在一起。对象的方法和原型链是理解JavaScript中面向对象编程的关键概念。本文将详细讲解对象的方法和原型链,用通俗易懂的方式帮助你深入理解这些概念。 1. 对象…...

Oracle入门初探---第一章 批量创建表、索引并插入测试数据
Oracle系列文章目录 第一章 批量创建表并插入测试数据 文章目录 Oracle系列文章目录前言一、创建表和索引二、向表中加入数据总结 前言 使用数据库,首先要向数据库中加入大量数据,本篇文章提供了一些测试数据 一、创建表和索引 -- 创建数据库和索引 -…...
全面讲解最小二乘法
常见的最小二乘法我们就不多说了,下面主要介绍一下最小二乘法的一些先进方法。 正则化的最小二乘法 在使用常见的最小二乘法进行回归分析时,常常会遇到过拟合的问题,也就是在训练数据集上表现的很好,但是在测试数据集上表现的很…...
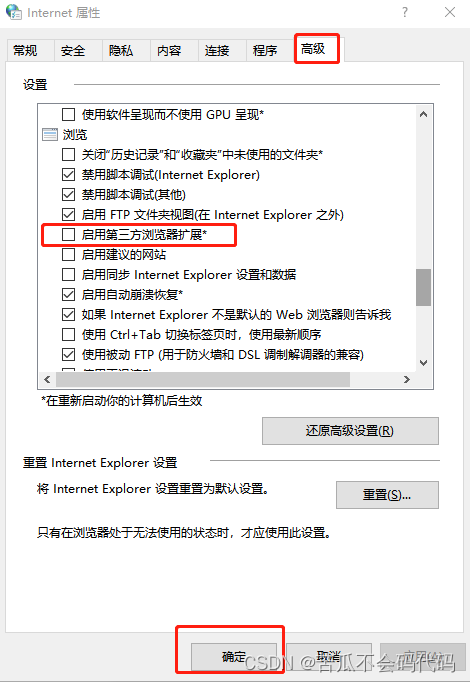
【阻止IE强制跳转到Edge浏览器】
由于微软开始限制用户使用Internet Explorer浏览网站,IE浏览器打开一些网页时会自动跳转到新版Edge浏览器,那应该怎么禁止跳转呢? 1、点击电脑左下角的“搜索框”或者按一下windows键。 2、输入“internet”,点击【Internet选项…...
)
C++/Linux项目——日志系统(简介)
一,日志系统的目的 1.⽣产环境的产品为了保证其稳定性及安全性是不允许开发⼈员附加调试器去排查问题, 可以借助⽇志系统来打印⼀些⽇志帮助开发⼈员解决问题 2.上线客⼾端的产品出现bug⽆法复现并解决, 可以借助⽇志系统打印⽇志并上传到服…...

【Redis面试题整理一】
一、Redis定义 Redis 是一种基于内存的数据库,对数据的读写操作都是在内存中完成,读写速度非常快,被广泛应用于缓存方向。并且,Redis 存储的是 KV 键值对数据。 二、Redis为什么不存在并发竞争 对数据类型的操作都是原子性的&a…...

前端权限验证之自定义指令v-permission
自定义指令 在前端处理按钮权限详细代码 在前端处理按钮权限 使用vue自定义指令来v-permission 来控制按钮 详细代码 //index.js文件 import permission from ./permissionconst install function(Vue) {Vue.directive(permission, permission) }if (window.Vue) {window[p…...
)
c++使用条件变量实现生产消费问题(跨平台)
1. 生产者线程 思路:队列满了的情况下, 触发条件变量wait, 等待消费线程消费后唤醒继续生产. void ProducerThreadFunc() {while(1) { while(/* 容器已满 */) { /* 线程等待, 直到消费者消费后唤醒继续执行 */ }/* 生产动作 */ } }2. 消…...
怎么快速搭建BI?奥威BI系统做出了表率
搭建BI系统有两大关键,分别是环境搭建和数仓建设。这两点不管是哪一个都相当地费时费力,那要怎么才能快速搭建BI平台,顺利实现全企业数字化运营决策?奥威BI系统方案,你值得拥有! 奥威BI系统方案࿰…...
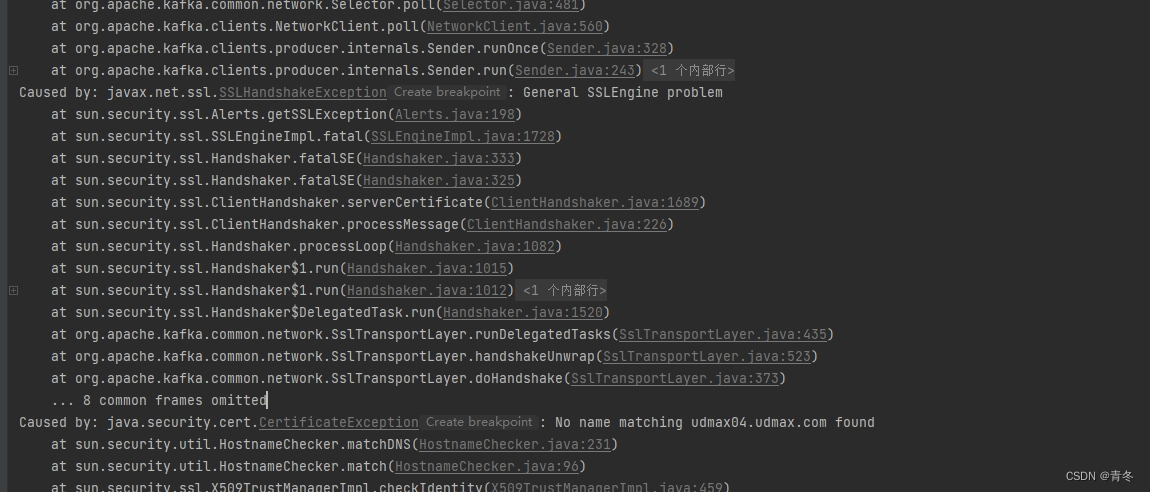
Kafka3.4 SASL/kerberos/ACL 证以及 SSL 加密连接
Kafka3.4 SASL/kerberos ACL 证以及 SSL 加密连接 序 前面我们使用 kafka3.3.1 on zookeeper 的模式进行多网段监听的 kafka 集群,顺便搭建起 kafkaui 后发现一些问题,我们 kafka 集群没有连接认证,万一谁知道了我们的 kafka 连接地址&…...
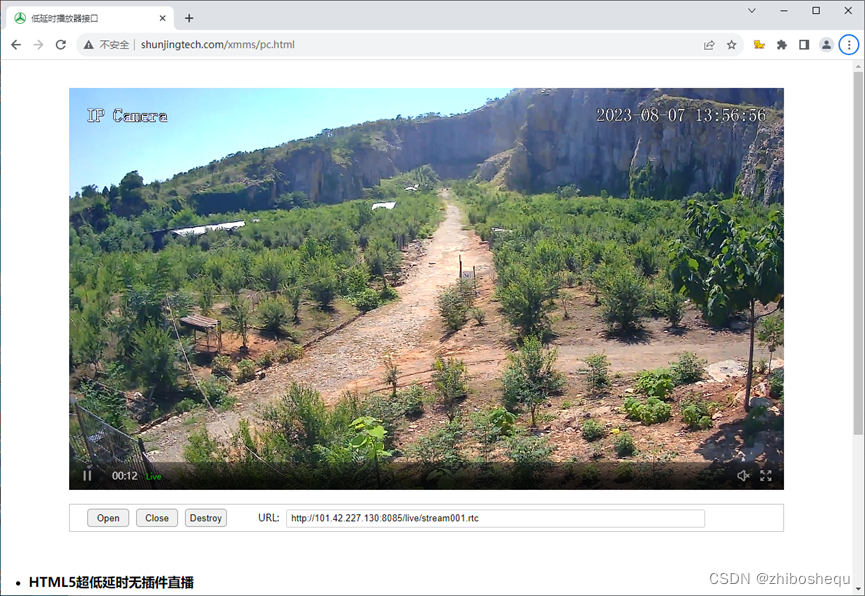
UE中低延时播放RTSP监控视频解决方案
第1章 方案简介 1.1 行业痛点 在各种智慧城市、智慧社区、智慧水利、智慧矿山等数字孪生项目中,经常使用通UE来开发三维可视化场景。在这些场景中通常都需要把现场的各种监控视频在UE的可视化场景中接入,主要包含海康威视、大华、宇视、华为等众多监控…...
iOS - 开发者账号续订会员资格更换订阅的账号
文章目录 前言开发环境续订会员资格转让账户持有人验证身份1. 实名认证2. 联系信息 更换订阅的账号最后 前言 公司有一个开发者账号快到期了需要续订会员资格,刚注册时是用我自己的个人账号完成的订阅购买。现在想来有点不妥,于是尝试更换用于订阅的账号…...

大数据课程F3——HIve的基本操作
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握HIve的基本SQL语句和注意问题; ⚪ 掌握HIve的表结构; ⚪ 掌握HIve的数据类型; ⚪ 掌握HIve的基础函数和窗口函数; 一、基本SQL 1. SQL的执行方式 1. 通过hive -e的方式来执行指…...

top解析
top - 13:52:26 up 26 days, 20:56, 2 users, load average: 0.00, 0.01, 0.05 当前时间 系统运行时间,格式为时:分 当前登陆用户数2 系统负载,即任务队列的平均长度。三个数值分别为1分钟,5分钟,15分钟前到现在的平均…...

如何让子组件,router-view,呈现左右分布格局
1.用浮动进行浮动布局,定义一个大盒子,把浮动的样式写在公共样式里(这里在main.js里定义一下全局布局)。 2、能够在右边显示了...
计算机网络—TCP和UDP、输入url之后显示主页过程、TCP三次握手和四次挥手
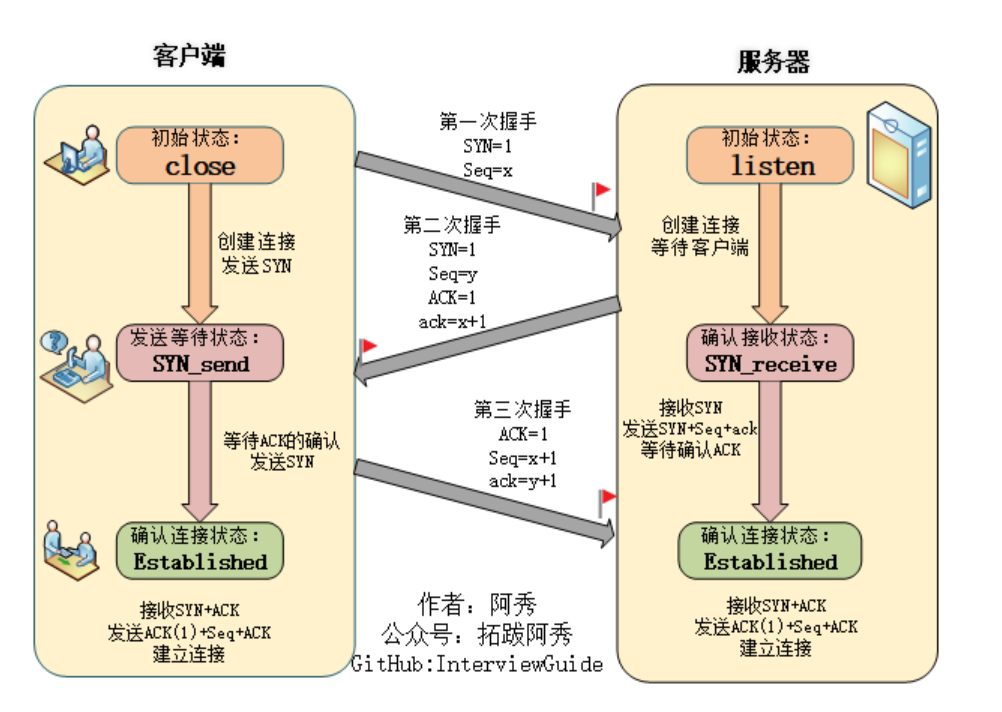
TCP基本认识 TCP是面向连接的、可靠的,基于字节流的传输层通信协议。 图片来源小林coding 序号:传输方向上字节流的字节编号。初始时序号会被设置一个随机的初始值(ISN),之后每次发送数据时,序号值 ISN…...
使用反汇编工具IDA查看发生异常的汇编代码的上下文去辅助分析C++软件异常
目录 1、概述 2、如何使用IDA打开并查看二进制文件的汇编代码 3、在IDA中找到发生崩溃的那条汇编指令的位置 3.1、如何在IDA中找到发生异常的那条汇编指令 3.2、示例 4、阅读汇编代码上下文需要掌握一定的基础汇编知识 5、最后 VC常用功能开发汇总(专栏文章列…...
怎么合并多个视频?简单视频合并方法分享
合并多个视频可以将它们组合成一个更长的视频,这对于需要播放多个短视频的情况非常有用。此外,合并视频还可以使视频编辑过程更加高效,因为不必将多个独立的视频文件分别处理。最后,合并视频可以减少文件数量,从而使整…...
webpack基础知识九:如何提高webpack的构建速度?
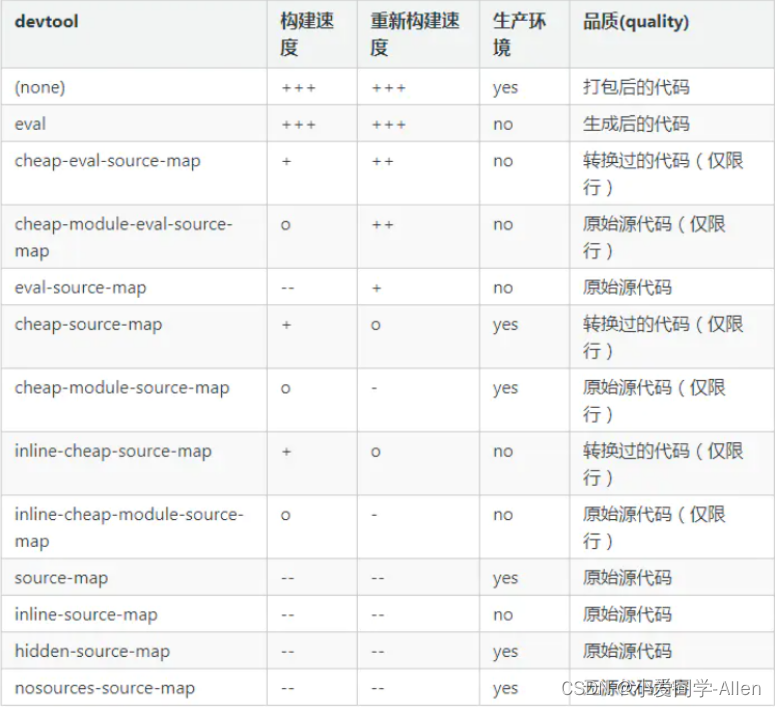
一、背景 随着我们的项目涉及到页面越来越多,功能和业务代码也会随着越多,相应的 webpack 的构建时间也会越来越久 构建时间与我们日常开发效率密切相关,当我们本地开发启动 devServer 或者 build 的时候,如果时间过长ÿ…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
