动态规划(用空间换时间的算法)原理逻辑代码超详细!参考自《算法导论》
动态规划(用空间换时间的算法)-实例说明和用法详解
- 动态规划(DP)思想
- 实例说明
- 钢条切割问题
- 矩阵链乘法问题
- 应用满足的条件和场景
本篇博客以《算法导论》第15章动态规划算法为本背景,大量引用书中内容和实例,并根据书中伪代码给出python代码复现,详解算法的核心逻辑和实现过程。
动态规划(DP)思想
动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为重叠的子问题进行解决,从而一步步获取最优解的处理算法。
动态规划与分治方法相似,都是通过组合子问题的解来求解原问题(在这里“programming”指的是一种表格法,并非编写计算机序)。但是分治方法将问题划分为互不相交的子问题,递归地求解子问题,再将它们的解组合起来,求出原问题的解。与之相反,动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子问题(子问题的求解是递归进行的,将其划分为更小的子子问题)。
在这种情况下,分治算法会做许多不必要的工作,它会反复地求解那些公共子子问题。而动态规划算法对每个子子问题只求解一次,将其解保存在一个表格中,从而无需每次求解一个子子问题时都重新计算,避免了这种不必要的计算工作。
实例说明
动态规划方法常用来求解最优化问题,下面分别给出二个例子来说明:第一个是将钢条割成短钢条,使得总价值最高;第二个是解决如何用最少的标量乘法操作完成一个矩阵链相乘的运算
钢条切割问题
下面是钢条切割问题的背景:

比如,下图给出长度为4英寸钢条所有可能的切割方案:
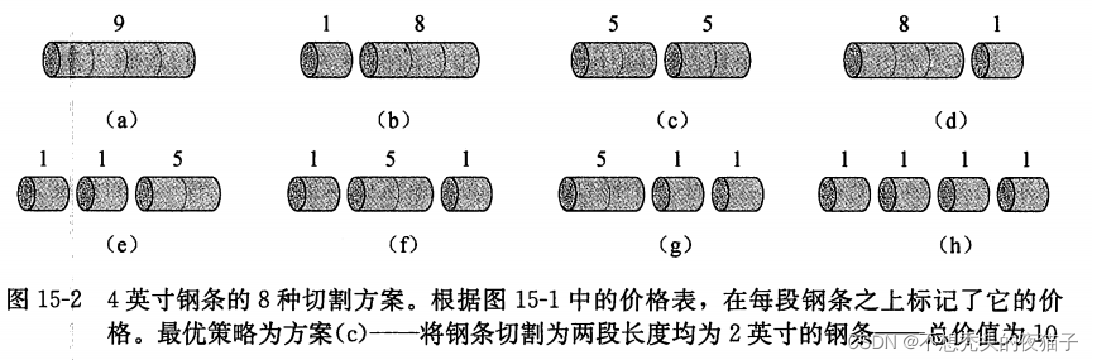
其中,钢条上方的数字为每段钢条对应的价格。不同的切割方案对应不同的价格,我们发现,将一段长度为4英寸的钢条切为两段各长2英寸的钢条,将产生 P 2 P_2 P2+ P 2 P_2 P2=5+5=10的收益,为最优解,即对应上图中的方案C。
下面我们逐步分析出钢条切割问题的最优收益的递推公式:

更为一般的收益公式,长度为n的钢条切割后的最大收益 r n r_n rn表示如下:

一种更简单的递归方法:

其中,(15.2)式中的 p i p_i pi指长度为i的钢条对应的价格,直接查表得到,不用再进行切割。
如果用传统的递归方法求解,一旦n的规模稍微变大,程序运行的时间会变得相当长,因为这种方法反复用相同的参数值对自身进行递归调用,即它反复求解相同的子问题。时间呈指数级增长。下图给出n=4时,递归树的调用过程:
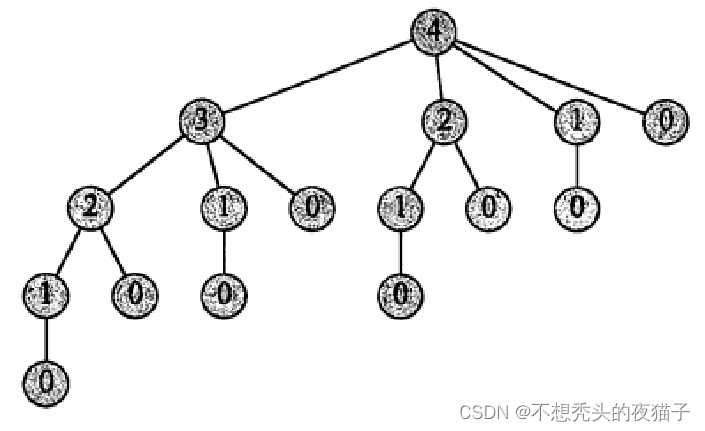
动态规划方法的运行时间是多项式阶的。

动态规划有两种等价的实现方法:

下面给出自底向上法的代码实现过程:

在上面的伪代码中,输入为两个变量,价格表数组和长度n;输出长度为n的钢条得到的最优收益。
下面计算长度为9时,钢条切割的最大收益:
import numpy as npdef Bottom_Up_Cut_Rod(p, n):r = []r.insert(0, 0)for j in range(1, n + 1):q = float('-inf')for i in range(1, j + 1):q = max(q, p[i - 1] + r[j - i])r.insert(j, q)return r[n]if __name__ == '__main__':# 出售长度为i(i=1,2,3,,,10)的钢条所对应的价格样表p = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]n = 9result = Bottom_Up_Cut_Rod(p, n)print("长度为{}时,".format(n))print("对应的最优收益值为{}。".format(result))
下图是长度为1、2、3…,对应的最优切割方案和收益。

思想:为了求解规模为 n 的原问题,我们先求解形式完全一样,但规模更小的子问题。即当完成首次切割后,我们将两段钢条看成两个独立的钢条切割问题实例。我们通过组合两个相关子问题的最优解,并在所有可能的两段切割方案中选取组合收益最大者,构成原问题的最优解。
我们称钢条切割问题满足最优子结构性质:问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解。
矩阵链乘法问题
矩阵链乘法问题即是多个矩阵相乘,找出最快计算次序的问题。

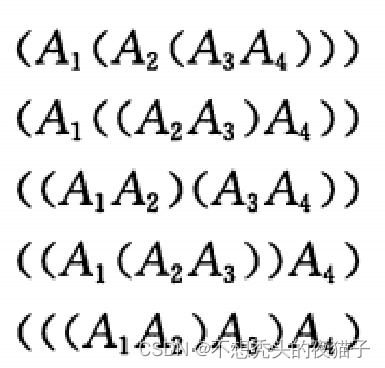
对矩阵链加括号的方式会对乘积运算的代价产生巨大影响,下面举例来说明:

因此,如果A是pXq的矩阵,B是qXr的矩阵,那么乘积 C是pXr的矩阵。计算 C所需时间由标量乘法的次数决定,即 pqr。下面我们将用标量乘法的次数来表示计算代价。

传统方法:穷举所有可能的括号化方案不会是一个高效的算法,因为它的运行时间仍然是指数级增长的。
下面定义矩阵链问题的计算代价公式,令m[i,j]表示计算矩阵 A i , . . . , j A_{i,...,j} Ai,...,j所需标量乘法次数的最小值。


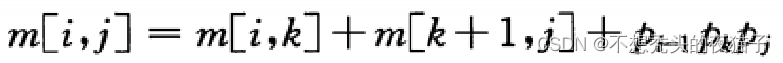
假设最优分割点k是未知的,则递归求解公式变为:
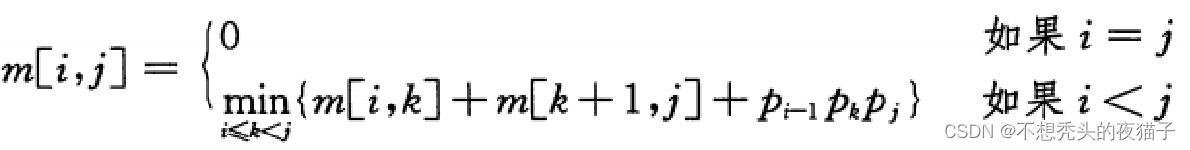
下面用一个例子来说明:

上图是我手写的一个例子,为了帮助理解。其中, A 1 A_1 A1:2 × \times × 3 ,表示 A 1 A_1 A1的维度为2行3列,P列表存放的是四个矩阵的维度,其中前一个矩阵的列数等于后一个矩阵的行数。要求出 A 1 A_1 A1 A 2 A_2 A2 A 3 A_3 A3 A 4 A_4 A4的计算代价,假设分割点k=2,则计算顺序为 ( ( A 1 A 2 ) ( A 3 A 4 ) ) ((A_1A_2)(A_3A_4)) ((A1A2)(A3A4))。其中, ( A 1 A 2 ) (A_1A_2) (A1A2)的计算代价对应上图中的矩阵C, ( A 3 A 4 ) (A_3A_4) (A3A4)的计算代价对应上图中的矩阵D,最后再令C与D相乘,算的最后的计算代价(总次数)为48。
下面给出的过程 MATRIX-CHAIN-ORDER实现了自底向上表格法:
各输入变量的含义如下:


输出变量为最优代价矩阵m和最优分割点矩阵k。
下面给出代码的计算过程帮助理解。假设n=4, p = [ p 0 , p 1 , p 2 , p 3 , p 4 ] p = [p_0,p_1,p_2,p_3,p_4] p=[p0,p1,p2,p3,p4],求 A 1 A 2 A 3 A 4 A_1A_2A_3A_4 A1A2A3A4的最优代价,即求m[1,4]。计算过程如下:


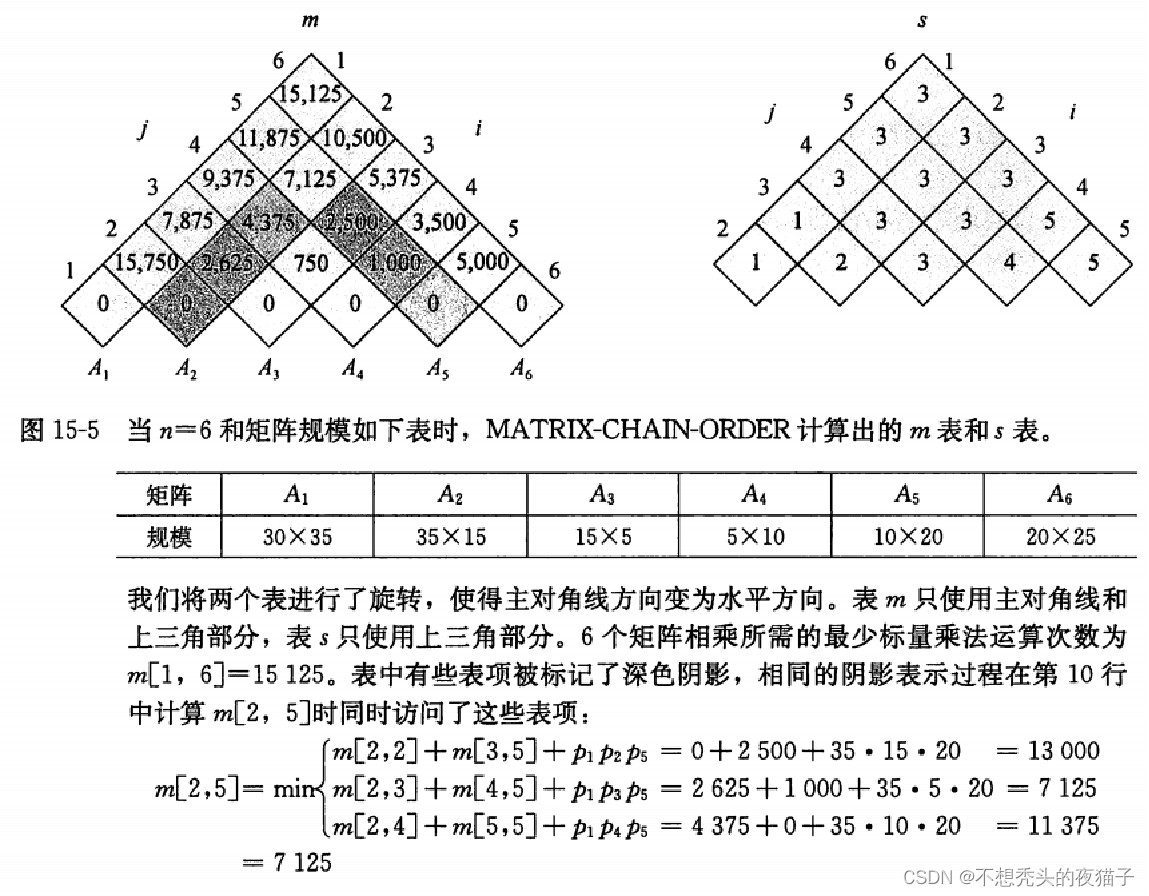
左边是最优代价矩阵,右边是最优分割点矩阵。
以图15-5的数据为例,python代码如下:
import numpy as npdef MATRIX_CHAIN_ORDER(p):n = len(p) - 1# 定义计算代价矩阵mm = np.zeros((n, n))# 定义最优分割点矩阵ss = np.zeros((n, n))for l in range(2, n + 1):for i in range(1, n - l + 2):j = i + l - 1m[i - 1, j - 1] = float('inf')for k in range(i, j):q = m[i - 1, k - 1] + m[k, j - 1] + p[i - 1] * p[k] * p[j]if q < m[i - 1, j - 1]:m[i - 1, j - 1] = qs[i - 1, j - 1] = kprint(m) # 每个元素对应长度为j-i+1的矩阵所需要最小计算代价print(s) # 对应长度为j-i+1的矩阵最优分割点return m, sif __name__ == '__main__':p = [30, 35, 15, 5, 10, 20, 25]MATRIX_CHAIN_ORDER(p)运行结果如下:
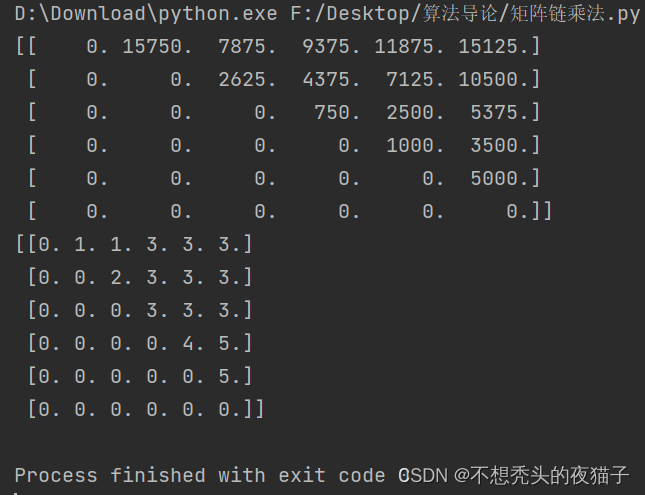
能够看出,跑出的结果与书上的两个矩阵完全相同。(只不过书中对矩阵沿主对角线方向进行了旋转)
思路:一个非平凡的矩阵链乘法问题实例的任何解都需要划分链,而任何最优解都是由子问题实例的最优解构成的。因此,为了构造一个矩阵链乘法问题实例的最优解,我们可以将问题划分为两个子问题( A i A i + 1 ⋅ ⋅ ⋅ A k A_iA_{i+1}···A_k AiAi+1⋅⋅⋅Ak和 A k + 1 ⋅ ⋅ ⋅ A j A_{k+1}···A_j Ak+1⋅⋅⋅Aj)子题实例的最优解,然后将子问题的最优解组合起来。我们必须保证在确定分割点时,已经考察了所有可能的划分点,这样就可以保证不会遗漏最优解。
应用满足的条件和场景
应用动态规划方法求解的最优化问题应该具备的两个要素:最优子结构和子问题重叠。


动态规划算法可以用来求解最优化问题,除了本文给出的两个例子外,常用的场景包括求解斐波那契数列,求解最长公共子序列、01背包问题和最优二叉搜索树等。想要深入了解该算法的原理和应用场景,具体可以阅读《算法导论》,我有电子版的,需要的兄弟姐妹可以私信我取。
综上所述,满足最优子结构和子问题重叠性质的问题可以利用动态规划思想建模,这种方法会开辟内存,存储以往的运算结果,再下次遇到时直接调用而不再重复计算,因此大大节省了时间,是一种经典的用空间换时间的算法,而大多数情况下,项目对时间的要求往往更严格,相比对内存的占用情况就宽松很多了。
相关文章:

动态规划(用空间换时间的算法)原理逻辑代码超详细!参考自《算法导论》
动态规划(用空间换时间的算法)-实例说明和用法详解 动态规划(DP)思想实例说明钢条切割问题矩阵链乘法问题 应用满足的条件和场景 本篇博客以《算法导论》第15章动态规划算法为本背景,大量引用书中内容和实例࿰…...

Jmeter添加cookie的两种方式
jmeter中添加cookie可以通过配置HTTP Cookie Manager,也可以通过HTTP Header Manager,因为cookie是放在头文件里发送的。 实例:博客园点击添加新随笔 https://i.cnblogs.com/EditPosts.aspx?opt1 如果未登录,跳转登录页…...
【ArcGIS Pro二次开发】(58):数据的本地化存储
在做村规工具的过程中,需要设置一些参数,比如说导图的DPI,需要导出的图名等等。 每次导图前都需要设置参数,虽然有默认值,但还是需要不时的修改。 在使用的过程中,可能会有一些常用的参数,希望…...

React配置代理服务器的5种方法
五种方法的介绍 以下是五种在React项目中配置代理服务器的方法的使用场景和优缺点: 1. 使用 http-proxy-middleware 中间件: 使用场景:适用于大多数React项目,简单易用。优点:配置简单,易于理解和维护。…...

树莓派:5.jar程序自启运行
搞了好长时间才搞定,普通的jar文件好启动。神奇的在于在ssh里启动GPIO可以操作,但是自启动GPIO不能控制。第二天才想明白估计是GPIO的操作权限比较高,一试果然如此,特此记录。 1、copy程序文件和sh文件在Public下 piraspberrypi…...

Vivado中SmartConnect和InterConnect的区别
前言:本文章为FPGA问答系列,我们会定期整理FPGA交流群(包括其他FPGA博主的群)里面有价值的问题,并汇总成文章,如果问题多的话就每周整理一期,如果问题少就每两周整理一期,一方面是希…...

了解HTTP代理日志:解读请求流量和响应信息
嗨,爬虫程序员们!你们是否在了解爬虫发送的请求流量和接收的响应信息上有过困扰?今天,我们一起来了解一下。 首先,我们需要理解HTTP代理日志的基本结构和内容。HTTP代理日志是对爬虫发送的请求和接收的响应进行记录的文…...

排序-堆排序
给你一个整数数组 nums,请你将该数组升序排列。 输入:nums [5,2,3,1] 输出:[1,2,3,5] 输入:nums [5,1,1,2,0,0] 输出:[0,0,1,1,2,5] 思路直接看我录制的视频吧 算法-堆排序_哔哩哔哩_bilibili 实现代码如下所示&…...

挑战Open AI!!!马斯克宣布成立xAI.
北京时间7月13日凌晨,马斯克在Twitter上宣布:“xAI正式成立,去了解现实。”马斯克表示,推出xAI的原因是想要“了解宇宙的真实本质”。Ghat GPT横空出世已有半年,国内外“百模大战”愈演愈烈,AI大模型的现状…...
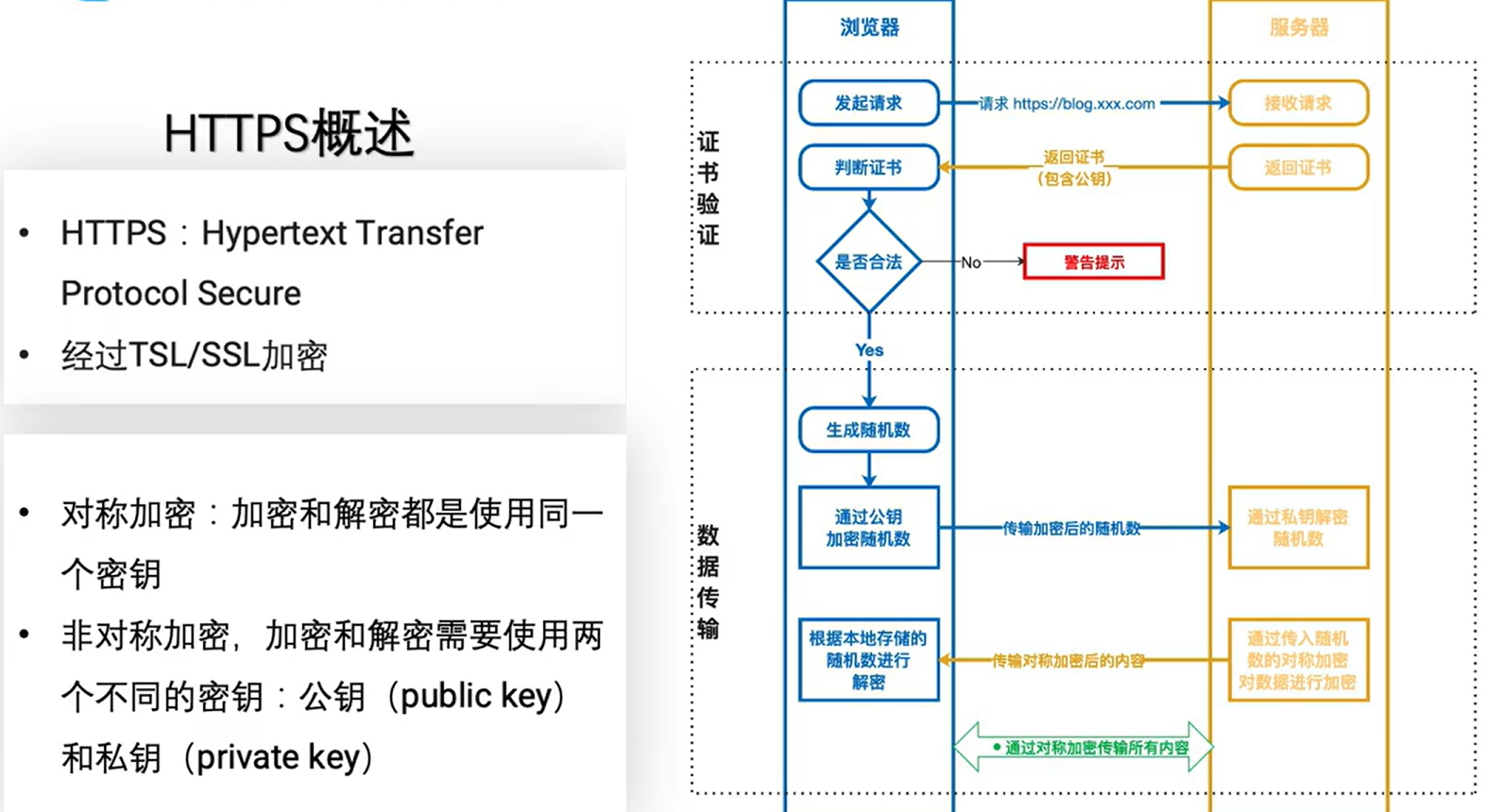
HTTP协议学习笔记1
初识HTTP 输入网址进入网页过程发生了什么? DNS解析:浏览器会向本地DNS服务器发出域名解析请求,如果本地DNS服务器中没有对应的IP地址,则会向上级DNS服务器继续发出请求,直到找到正确的IP地址为止。 建立TCP连接&…...
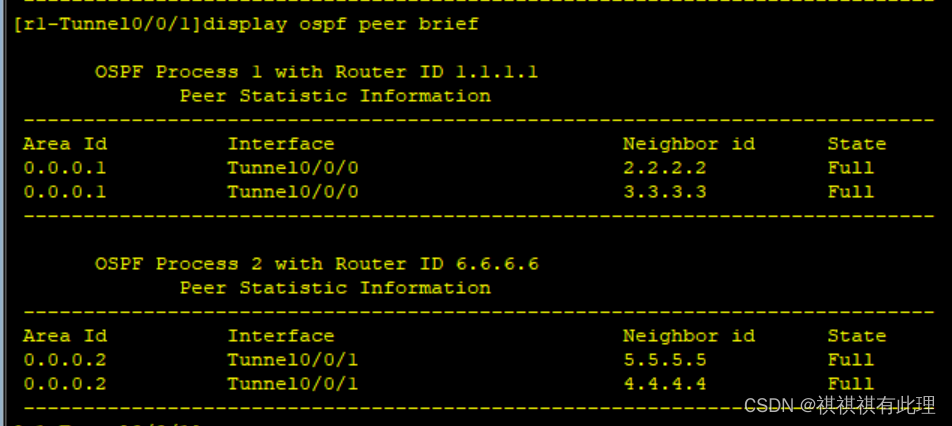
【网络基础实战之路】基于OSPF协议建立两个MGRE网络的实验详解
系列文章传送门: 【网络基础实战之路】设计网络划分的实战详解 【网络基础实战之路】一文弄懂TCP的三次握手与四次断开 【网络基础实战之路】基于MGRE多点协议的实战详解 【网络基础实战之路】基于OSPF协议建立两个MGRE网络的实验详解 PS:本要求基于…...

【学习日志】2023.Aug.6,支持向量机的实现
2023.Aug.6,支持向量机的实现 参考了大佬的代码,但有些地方似乎还有改进的空间,我加了注释 #codingutf-8 #Author:Dodo #Date:2018-12-03 #Email:lvtengchaopku.edu.cn #Blog:www.pkudodo.com数据集:Mnist 训练集数量࿱…...

LeetCode_动态规划_中等_1749.任意子数组和的绝对值的最大值
目录 1.题目2.思路3.代码实现(Java) 1.题目 给你一个整数数组 nums 。一个子数组 [numsl, numsl1, …, numsr-1, numsr] 的 和的绝对值 为 abs(numsl numsl1 … numsr-1 numsr) 。请你找出 nums 中和的绝对值 最大的任意子数组(可能为空…...

无涯教程-Perl - 环境配置
在开始编写Perl程序之前,让我们了解如何设置我们的Perl环境。 您的系统更有可能安装了perl。只需尝试在$提示符下给出以下命令- $perl -v 如果您的计算机上安装了perl,那么您将收到以下消息: This is perl 5, version 16, subversion 2 (v5.16.2) b…...

QT显示加载动画
文章目录 一、前言二、使用1.FormLoading.h2.FormLoading.cpp 一、前言 项目中在下发指令时,结果异步返回,可能需要一段时间,因此需要用到加载动画。 用的比较简单,就是新建Widget子窗口,放一个Label,使用…...
原型模式(C++)
定义 使用原型实例指定创建对象的种类,然后通过拷贝这些原型来创建新的对象。 应用场景 在软件系统中,经常面临着“某些结构复杂的对象”的创建工作;由于需求的变化,这些对象经常面临着剧烈的变化,但是它们却拥有比较稳定一致的…...

web浏览器打开本地exe应用
一、如何使web浏览器打开本地exe应用? 浏览器打开本地exe程序我们可以使用ActiveXObject方法,但是只支持IE,谷歌、火狐等浏览器并不支持此操作。 那问题来了,我们又该如何操作? 经过本博主的不断学习探索终于找到了一…...
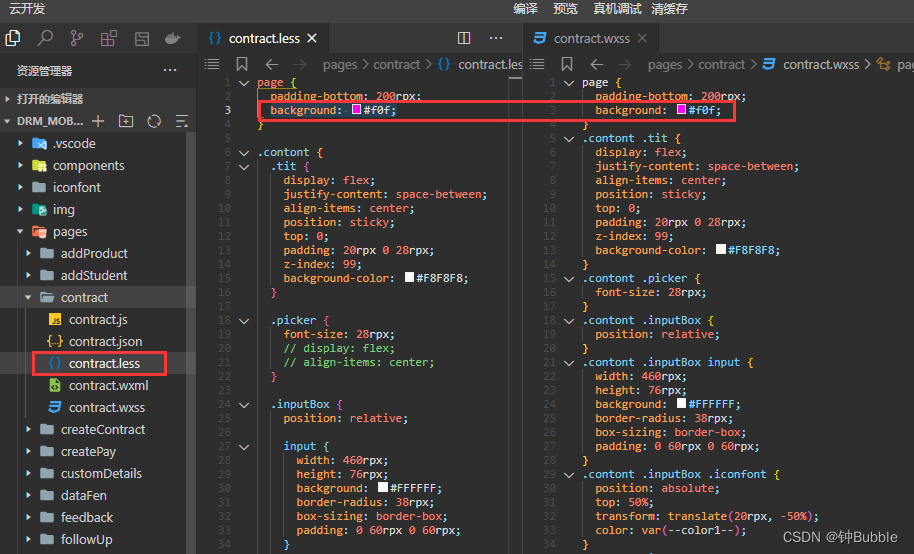
微信小程序如何配置并使用less?
1,检查微信开发者工具(工具版本1.03)————这步很重要不然后面按步骤实行后会发现急死你也还是不管用,我之前死在过这一步,所以大家不要再次踩坑了 ~ ~ 。。。 2,在VScode中下载Less插件 3,…...

【Spring】反射动态修改Bean实例的私有属性值
Cannot cast org.springframework.http.client.InterceptingClientHttpRequestFactory to org.springframework.http.client.OkHttp3ClientHttpRequestFactory 由于RestTemplate在自定义初始化时顺序比较早,想在启动后跟进yum或者注解配置修改初始化的值时ÿ…...

MySQL DDL 数据定义
文章目录 1.创建数据库2.删除数据库3.查看所有数据库4.查看当前数据库5.选择数据库6.创建数据表7.查看 MySQL 支持的存储引擎和默认的存储引擎8.删除数据表9.查看数据库的数据表10.查看表结构11.查看建表语句12.重命名数据表13.增加、删除和修改字段自增长14.增加、删除和修改数…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
