Matlab 最小二乘法拟合平面(SVD)
相关文章:
Matlab 最小二乘法拟合平面(SVD)
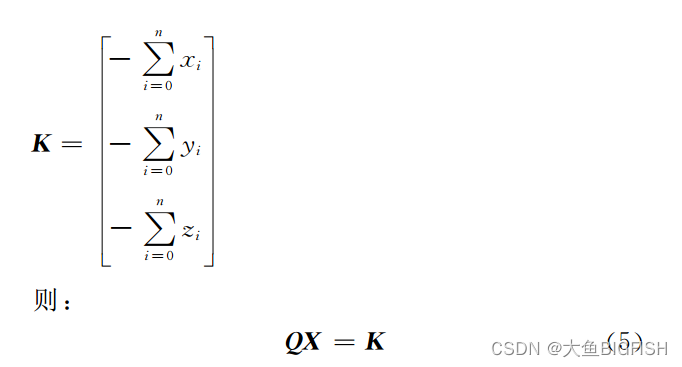
文章目录 一、简介1.1最小二乘法拟合平面1.2 SVD角度二、实现代码三、实现效果参考资料一、简介 1.1最小二乘法拟合平面 之前我们使用过最为经典的方式对平面进行了最小二乘拟合(点云最小二乘法拟合平面),其推导过程如下所示: 仔细观察一下可以发现...

AtCoder Regular Contest 126 D题题解
思路 首先我们看看假设选中 mmm 个数后的答案。 我们首先现将 mmm 个数移动到一起,在将他们重新排序。 我们知道,mmm 个数移在一起时,当位于中间的那个数不动时交换次数最少,于是可以列出式子(cic_ici 是点 iii 的…...

Android R WiFi热点流程浅析
Android R WiFi热点流程浅析 Android上的WiFi SoftAp功能是用户常用的功能之一,它能让我们分享手机的网络给其他设备使用。 那Android系统是如何实现SoftAp的呢,这里在FWK层面做一个简要的流程分析,供自己记录和大家参考。 以Android R版本为…...
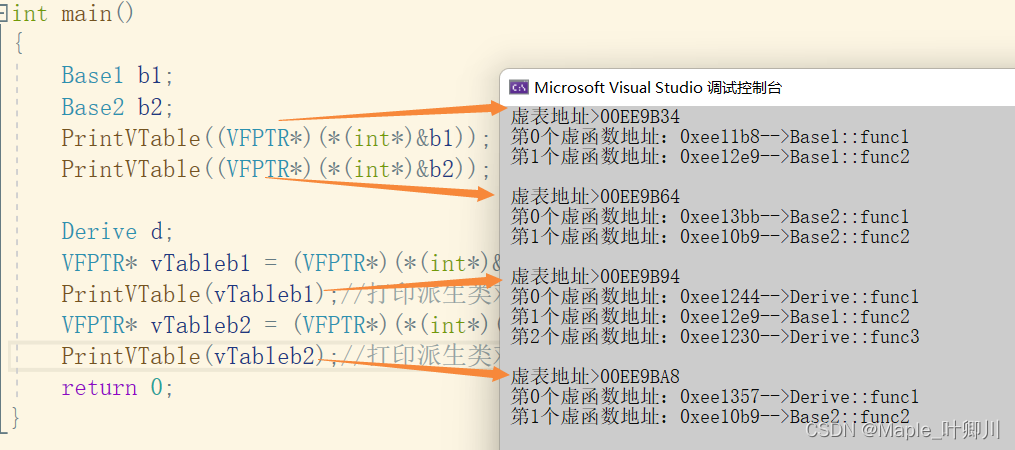
【C++进阶】二、多态详解(总)
目录 一、多态的概念 二、多态的定义及实现 2.1 多态的构成条件 2.2 虚函数 2.3 虚函数的重写 2.4 虚函数重写的两个例外 2.4.1 协变 2.4.2 析构函数的重写 2.5 C11 override 和 final 2.5.1 final 2.5.2 override 2.6 重载、覆盖(重写)、隐藏(重定义)的对比 三、…...
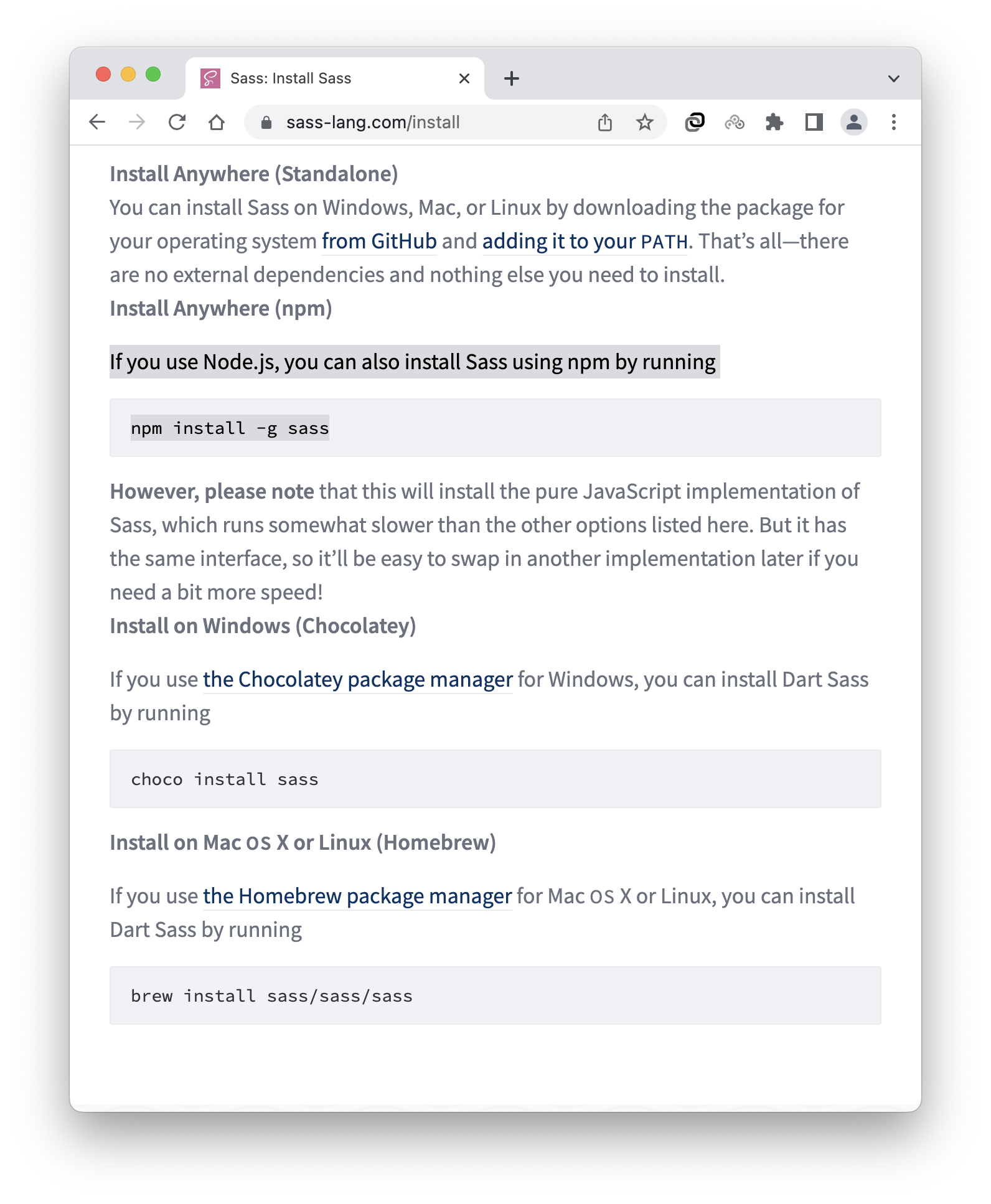
node-sass@4.14.1 包含风险, 如何升级依赖至 dart-sass
文章目录需求我上网都查到了哪些信息在 github 看到了 node-sass 依赖的最新版本的列表:关于方案2的失败不同版本的 nodejs 和 node-sass依赖的**适配关系**从何得知替代方案——dart-sass如何安装 dart sass?需求 在做一个基于Node、React的前端项目&a…...
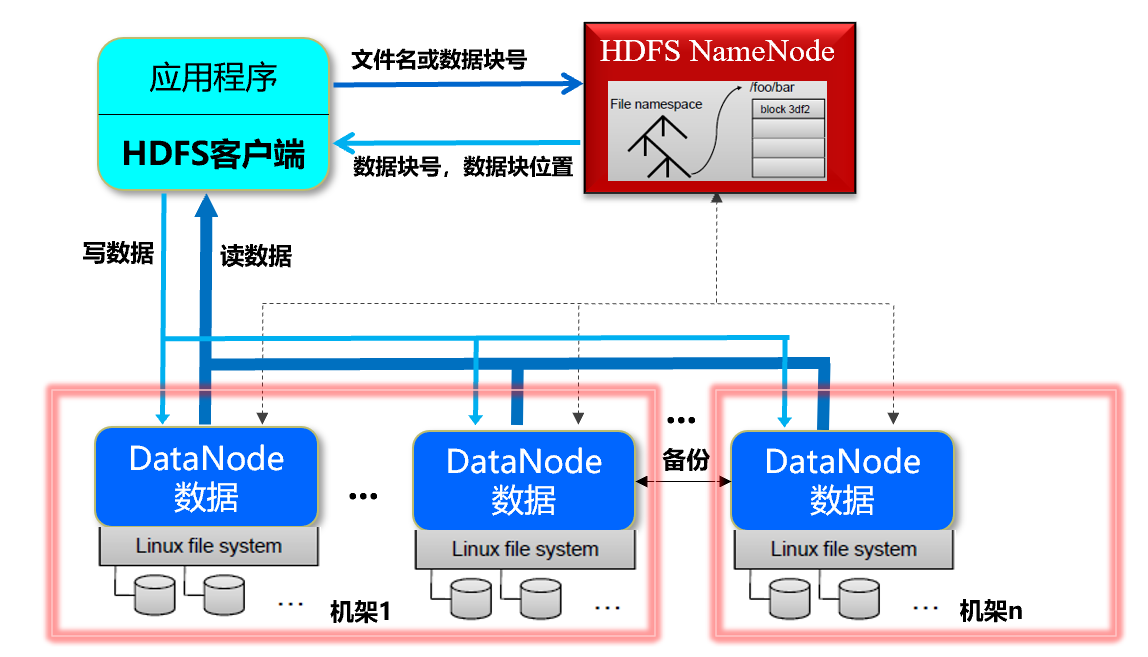
DataWhale 大数据处理技术组队学习task2
三、Hadoop分布式文件系统 1. 产生背景 数据量越来越大,一台独立的计算机已经无法存储所有的数据---->将大规模的数据存储到成百上千的计算机中------为了解决数据管理以及维护极其繁琐与低效------>分布式文件系统 分布式文件系统是管理网络中跨多台计算机…...

一文读懂select、poll、epoll的用法
select,poll,epoll都是IO多路复用的机制。I/O多路复用就通过一种机制,可以监视多个描述符,一旦某个描述符就绪(一般是读就绪或者写就绪),能够通知程序进行相应的读写操作。但select,…...

《C陷阱与缺陷》----词法“陷阱”
导言: 由于一个程序错误可以从不同层面采用不同方式进行考察,而根据程序错误与考察程序的方式之间的相关性,可以将程序错误进行划分为各种陷阱与缺陷: ①.词法“陷阱” ②.语法“陷阱” ③.语义“陷阱” ④.连接问题 ⑤.库函数问…...

千锋教育+计算机四级网络-计算机网络学习-04
UDP概述 UDP协议 面向无连接的用户数据报协议,在传输数据前不需要先建立连接;目地主机的运输层收到UDP报文后,不需要给出任何确认 UDP特点 相比TCP速度稍快些简单的请求/应答应用程序可以使用UDP对于海量数据传输不应该使用UDP广播和多播应用…...

蓝桥杯算法训练合集十四 1.P08052.P07053.同余方程4.P08015.ascii应用
目录 1.P0805 2.P0705 3.同余方程 4.P0801 5.ascii应用 1.P0805 问题描述 当两个比较大的整数相乘时,可能会出现数据溢出的情形。为避免溢出,可以采用字符串的方法来实现两个大数之间的乘法。具体来说,首先以字符串的形式输入两个整数&…...
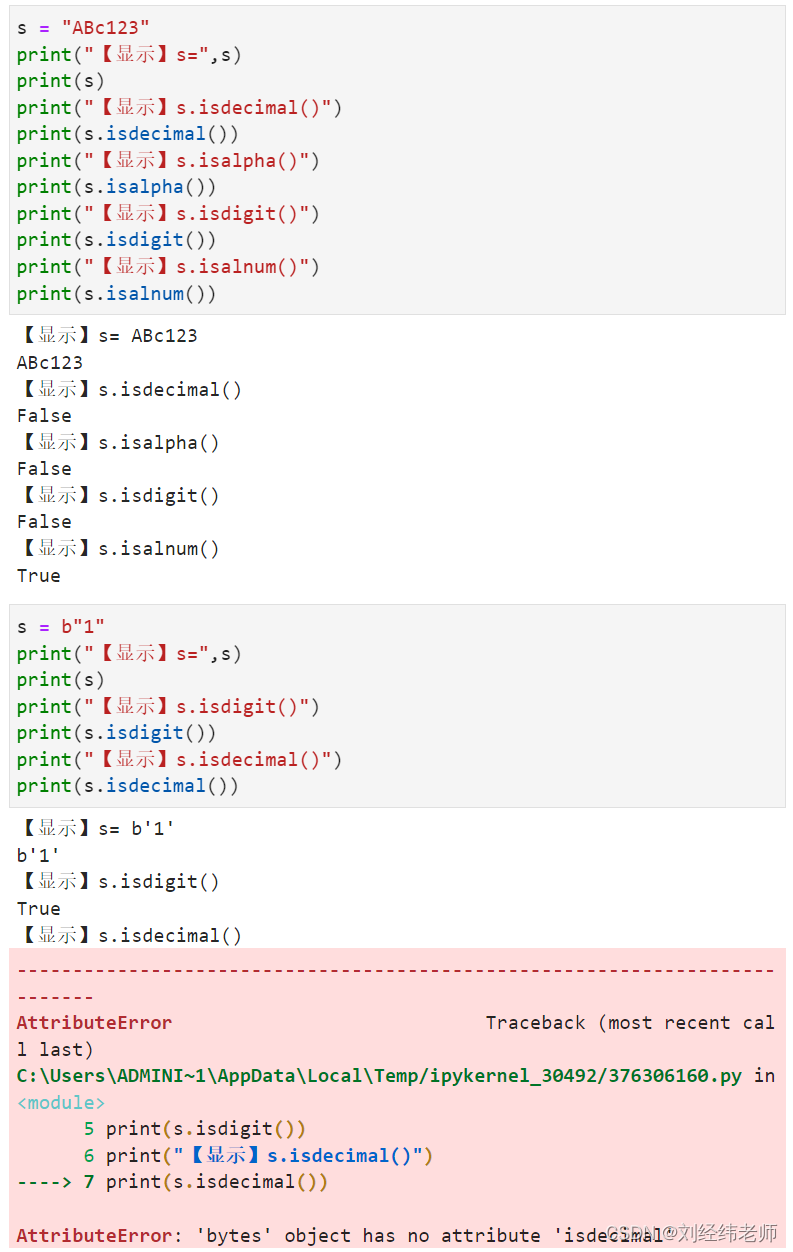
判断字符串中的字符的类型isdecimal();isalpha();isdigit();isalnum()
【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 判断字符串中的字符的类型 isdecimal();isalpha();isdigit();isalnum() [太阳]选择题 对于代码中isdecimal()和isalnum()输出的结果是? s "ABc123&…...
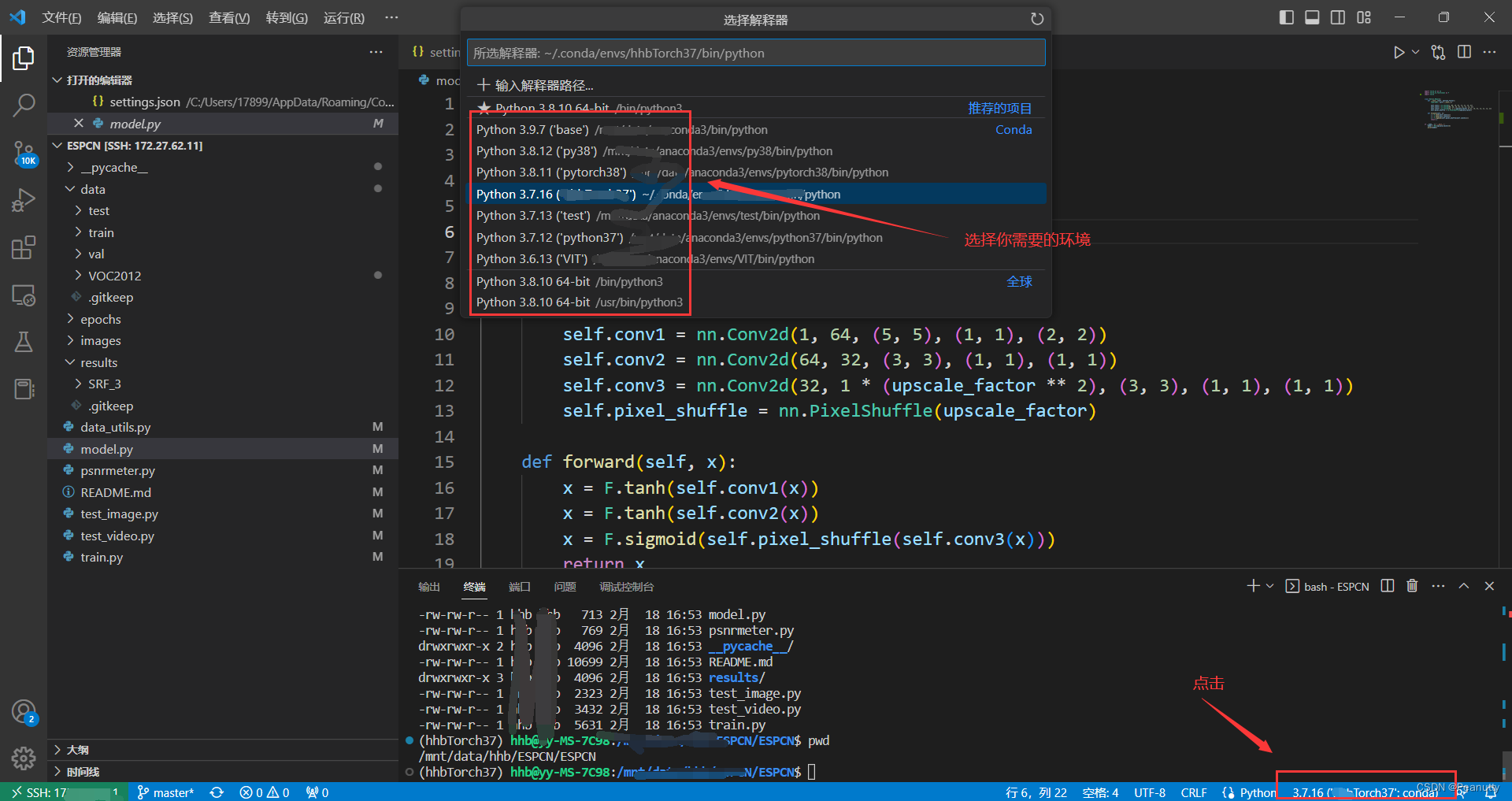
VSCode远程调试Linux代码,python解释器配置
安装插件并配置 安装后找到插件图标,点击 点击SSH上的 号 在弹出框中输入命令:ssh usernameip -p port username: 远程服务器的用户名 ip: 远程ip port:端口号,没有可以不用 输入完毕后点击enter 选择ssh配置文件保存…...

03:入门篇 - CTK Plugin Framework 基本原理
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 CTK Plugin Framework 技术是面向 C++ 的动态模型系统。该系统允许插件之间的松散耦合,并且提供了设计良好的方式来进行功能和数据的交互。此外,它没有预先对插件施加限制,这样就可以很容易地将插件的相关…...
)
面试攻略,Java 基础面试 100 问(九)
数组有没有 length()方法?String 有没有 length()方法? 数组没有 length()方法,有 length 的属性。String 有 length()方法。JavaScript 中,获得字符串的长度是通过 length 属性得到的,这一点容易和 Java混淆。 在 Java 中&…...

JavaScript 代码不嵌套主义
文章目录前言一、何为嵌套代码二、避免嵌套1.提炼抽取2.反转排列总结前言 看过不少过度嵌套的代码, 我真正意识到问题的严重性是刚入职那会, 我在一个老项目里看到了40个连续的else if, 套了6层的if, for和forEach, 因为我们并没有做什么限制代码嵌套的提前约定. 呃, 那之后认…...

使用默认参数的4大要点
概述 默认参数是C中新增的特性。在C中,可以为函数的参数指定默认值。调用函数时,如果没有指定实参,则自动使用默认参数。默认参数的基本语法这里就不作介绍了,下面重点介绍使用默认参数的一些知识要点。 基本规则 1、当函数中某个…...
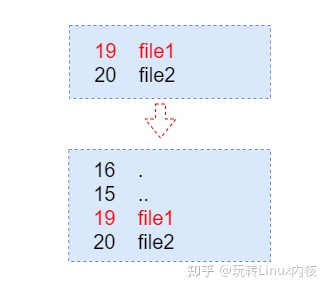
Linux文件系统中的硬链接及常见面试题
如果能对inode的概念有所了解,对理解本文会有所帮助。如果对inode的概念不太清楚也没有关系,我们会捎带介绍一下。在文件系统的实现层面,我们可以认为包含两个组件:一个是包含数据块的池子,池子中的数据块是等大小的&a…...

opencv-StereoBM算法
原理解释目前立体匹配算法是计算机视觉中的一个难点和热点,算法很多,但是一般的步骤是:A、匹配代价计算匹配代价计算是整个立体匹配算法的基础,实际是对不同视差下进行灰度相似性测量。常见的方法有灰度差的平方SD(squ…...

图像分类竞赛进阶技能:OpenAI-CLIP使用范例
OpenAI-CLIP 官方介绍 尽管深度学习已经彻底改变了计算机视觉,但目前的方法存在几个主要问题:典型的视觉数据集是劳动密集型的,创建成本高,同时只教授一组狭窄的视觉概念;标准视觉模型擅长于一项任务且仅擅长于一项任务,并且需要大…...
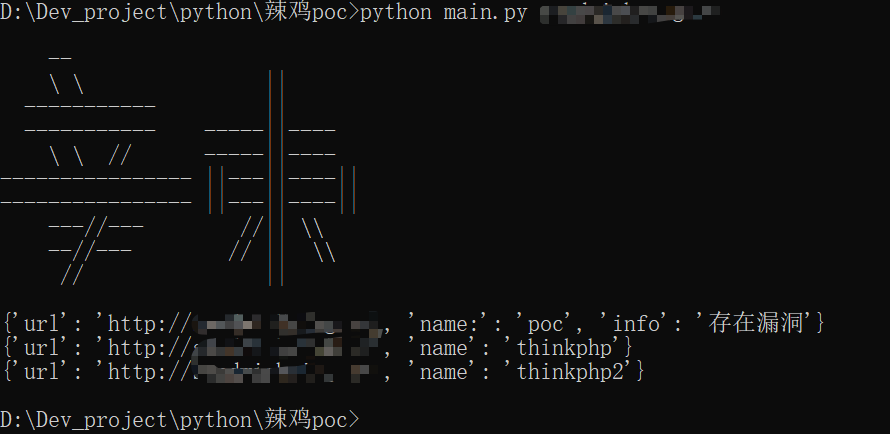
Metasploit框架基础(一)
文章目录前言一、基础认知二、批量POC/EXP的构想三、poc检测框架的简单实现四、xray五、Meatsploit框架参考前言 Metasploit 一款渗透测试框架漏洞利用的集合与构建和定制满足你的需求的基础漏洞利用和验证的工具 这几个说法都是百度或者官方文档中出现的手法,说…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...


