LeetCode105. 从前序与中序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树
文章目录
- [105. 从前序与中序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)
- 一、题目
- 二、题解
一、题目
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
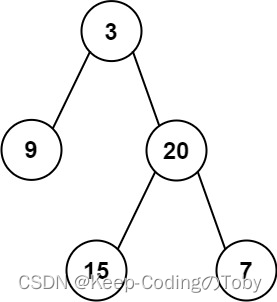
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
二、题解
算法思路:
我们要根据给定的前序遍历和中序遍历序列构建出一棵二叉树。前序遍历序列告诉我们根节点的值以及左子树和右子树的分割点,中序遍历序列告诉我们左子树和右子树的节点排列顺序。我们可以通过递归的方法来实现构建二叉树的过程。
具体步骤如下:
- 从前序遍历序列中取出第一个元素,它是当前子树的根节点的值。
- 在中序遍历序列中找到该根节点的值,根据这个值,将中序序列划分为左子树部分和右子树部分。
- 根据左子树和右子树的节点数量,在前序遍历序列中划分出左子树的前序序列和右子树的前序序列。
- 递归地构建左子树和右子树。
具体实现:
class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {// 基准情况:如果前序遍历序列为空,返回空指针表示空树if (preorder.size() == 0) {return nullptr;}// 创建当前子树的根节点TreeNode *root = new TreeNode();root->val = preorder[0];// 在中序遍历序列中找到根节点的位置int index = 0;for (index = 0; index < inorder.size(); index++) {if (inorder[index] == preorder[0]) {break;}}// 划分左子树和右子树的序列vector<int> leftPreorder(preorder.begin() + 1, preorder.begin() + index + 1);vector<int> leftInorder(inorder.begin(), inorder.begin() + index);vector<int> rightPreorder(preorder.begin() + index + 1, preorder.end());vector<int> rightInorder(inorder.begin() + index + 1, inorder.end());// 递归构建左子树和右子树root->left = buildTree(leftPreorder, leftInorder);root->right = buildTree(rightPreorder, rightInorder);return root;}
};
算法分析:
-
时间复杂度:在每次递归中,我们都需要遍历中序遍历序列来找到根节点的位置,这需要 O(n) 的时间,其中 n 是节点数量。递归的总时间复杂度取决于递归的层数以及每层的操作,因此总体时间复杂度为 O(n)。
-
空间复杂度:每次递归都会创建新的前序和中序序列,空间复杂度主要取决于递归的深度,最坏情况下递归深度为 n,所以空间复杂度为 O(n)。此外,还需要存储二叉树节点的空间,所以总体空间复杂度也为 O(n)。
相关文章:

LeetCode105. 从前序与中序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树 文章目录 [105. 从前序与中序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)一、题目二、题解 一、题目 给定两个整数数组 preorder 和 inorder ,其中 preo…...
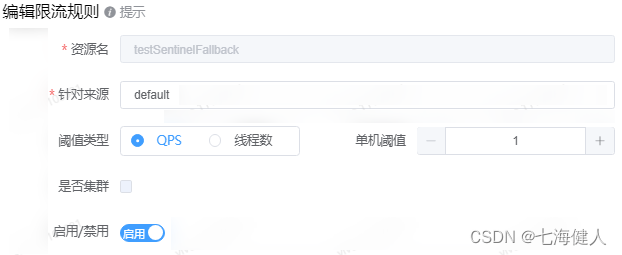
编码技巧——Sentinel的blockHandler与fallback
本文介绍Sentinel的blockHandler与fallback的区别,背景是:发生限流时,配置的sentinel的blockhandler没有生效而fallback生效了;排查原因,从而给出Sentinel配置异常降级和限流降级的代码写法; 在查看源码前…...

最新成果展示:GaN基Micro-LED热学模型数据库的开发及应用
由于GaN基Micro-LED表面积-体积比增加,其在热学方面的性质有别于大尺寸的LED,如缺陷复合导致的热效应将在发光区域中产生诸多“热”点,导致发光波长不均匀,这将影响后期显示系统的成像稳定性。针对上述问题,天津赛米卡…...

【Vue3】动态组件
动态组件的基本使用 动态组件(Dynamic Components)是一种在 Vue 中根据条件或用户输入来动态渲染不同组件的技术。 在 Vue 中使用动态组件,可以使用 元素,并通过 is 特性绑定一个组件的名称或组件对象。通过在父组件中改变 is 特…...

Java超级玛丽小游戏制作过程讲解 第五天 创建并完成常量类04
//加载障碍物 try {obstacle.add(ImageIO.read(new File(path"brick.png")));obstacle.add(ImageIO.read(new File(path"soil_up.png")));obstacle.add(ImageIO.read(new File(path"soil_base.png"))); } catch (IOException e) {e.printStackTr…...

设置浏览器兼容
浏览器兼容 css兼容 cursor定义手型 Firefox不支持hand,IE支持pointer 解决方法:统一使用pointercss透明 IE:filter:progid:DXImageTransform.Microsoft.Alpha(style0,opacity60) Firefox:opacity:0.6 解决…...

Java # List
ArrayList<>() import java.util.ArrayList; // 引入 ArrayList 类ArrayList<E> objectName new ArrayList<>(); // 初始化 常用方法 方法描述add()将元素插入到指定位置的 arraylist 中addAll()添加集合中的所有元素到 arraylist 中clear()删除 arrayl…...

git原理与使用
目录 引入基本操作分支管理远程操作标签管理 引入 假设你的老板要你设计一个文档,当你设计好了,拿给他看时,他并不是很满意,就要你拿回去修改,你修改完后,再给他看时,他还是不满意,…...
【C语言题解】将一句话的单词进行倒置,标点不倒置。
题目描述:将一句话的单词进行倒置,标点不倒置。比如 “I like beijing.”,经过处理后变为:“beijing. like I”。 文章目录 原题目题目描述:输入描述:输出描述:题目链接: 整体思路分…...
Postman 的简单使用
什么是Postman 在程序开发中用于调试网络程序或者跟踪网页请求。可以对网页进行简单的基本信息调试。Postman最早是作用chrome浏览器插件存在的,但是2018年初Chrome停止对Chrome应用程序的支持。所以现在Postman提供了独立的安装包,不再依赖于Chrome浏览…...

在CentOS7安装部署GitLab服务
CentOS 7 安装 Gitlab 官方安装教程:https://about.gitlab.com/install/ 参考安装教程:https://developer.aliyun.com/article/74395 安装配置 Step1:配置yum源 vim /etc/yum.repos.d/gitlab-ce.repo存入以下内容: [gitlab-c…...
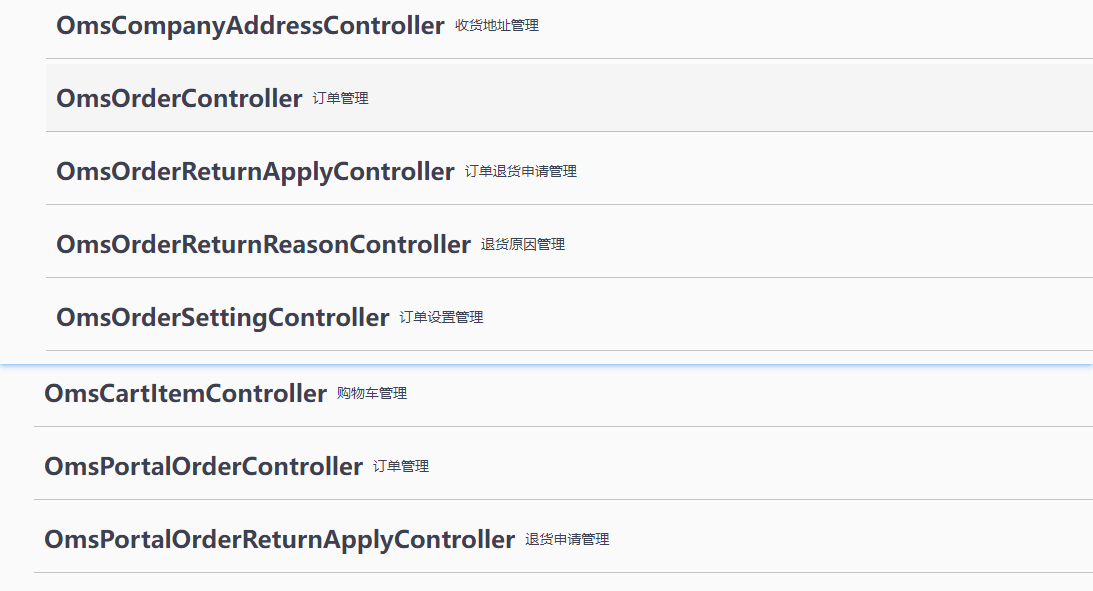
订单系统就该这么设计,稳的一批~
订单功能作为电商系统的核心功能,由于它同时涉及到前台商城和后台管理系统,它的设计可谓是非常重要的。就算不是电商系统中,只要是涉及到需要交易的项目,订单功能都具有很好的参考价值,说它是通用业务功能也不为过。今…...

Agents改变游戏规则,亚马逊云科技生成式AI让基础模型加速工作流
最近,Stability AI正式发布了下一代文生图模型——Stable Diffusion XL 1.0这次的1.0版本是Stability AI的旗舰版生图模型,也是最先进的开源生图模型。 在目前的开放式图像模型中,SDXL 1.0是参数数量最多的。官方表示,这次采用的…...
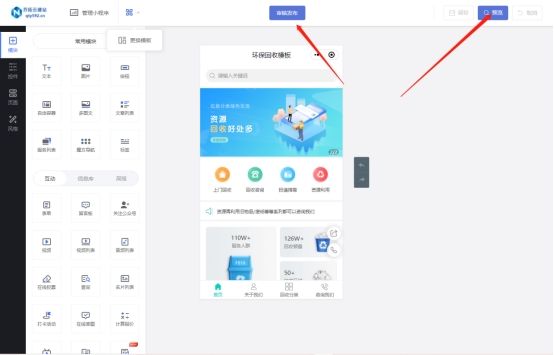
详细教程:如何搭建废品回收小程序
废品回收是一项环保举措,通过回收和再利用废弃物品,可以减少资源浪费和环境污染。近年来,随着智能手机的普及,小程序成为了推广和运营的重要工具。本文将详细介绍如何搭建一个废品回收小程序。 1. 进入乔拓云网后台 首先…...

什么是双亲委派机制?
什么是双亲委派机制? Parent Delegation Model ,直译过来可能叫做父级委托模型更容易理解 类的加载过程 Java 编译器将 Java源文件编译成.class 文件再由 JVM 加载 .class 文件到内存中JVM 装载完成后得到一个 Class 字节码对象拿到字节码对象之后 &a…...

Mageia 9 RC1 正式发布,Mandriva Linux 发行版的社区分支
导读Mageia 9 首个 RC 已发布。公告写道,自 2023 年 5 月发布 beta 2 以来,Mageia 团队一直致力于解决许多顽固问题并提供安全修复和新特性。 新版本的控制中心添加了用于删除旧内核的新功能,该功能在 Mageia 9 中默认自动启用,用…...

ChatGPT: 人机交互的未来
ChatGPT: 人机交互的未来 ChatGPT背景ChatGPT的特点ChatGPT的应用场景结论 ChatGPT ChatGPT是一种基于大数据和机器学习的人工智能聊天机器人模型。它由国内团队发明、开发,并被命名为Mental AI。ChatGPT的目标是通过模拟自然对话的方式,提供高效、智能…...
Linux 常用操作命令
Linux简介及Ubuntu安装 Linux,免费开源,多用户多任务系统。基于Linux有多个版本的衍生。RedHat、Ubuntu、Debian 安装VMware或VirtualBox虚拟机。具体安装步骤,找百度。 再安装Ubuntu。具体安装步骤,找百度。 常用指令 ls …...

24届近5年重庆邮电大学自动化考研院校分析
今天给大家带来的是重庆邮电大学控制考研分析 满满干货~还不快快点赞收藏 一、重庆邮电大学 学校简介 重庆邮电大学简称"重邮",坐落于直辖市-重庆市,入选国家"中西部高校基础能力建设工程”、国家“卓越工程师教育培养计划…...

如何对oracle和mysql进行 分区分表
前提:使用自带的分区和分表机制进行操作 oracle,mysql分区分表 分区 分区是一种将一个大的表或索引分割成多个小的部分的技术,每个部分称为一个分区。分区可以提高数据的管理和查询效率,因为可以根据不同的条件对不同的分区进行操作&#x…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
