SAP 订单BOM与销售BOM的区别
订单BOM与销售BOM的区别
訂單BOM: 是實際生產時用的BOM, 在標準BOM和銷售BOM基礎上增減物料的BOM 銷售BOM: 是為特定客戶設定的BOM, 在主檔數據層次上的BOM, 在生產時是帶到訂單BOM中去的.
標準BOM: 是公司為標準生產的BOM, 在主檔數據層次上的BOM, 在生產時是帶到訂單BOM中去的.
訂單BOM >= 銷售BOM >= 標準BOM
一般使用中:
訂單BOM是在銷售BOM的基礎或標準BOM基礎上添加部分物料或減少或修改實際需求數量,
銷售BOM是在標準BOM基礎上增加特定客戶需要的BOM, 例如顏色,
標準BOM是公司在標準生產中使用的BOM, 通常由工程設計BOM產出再進行修正, 在SAP的標準成本計算是需要用到的.
工程設計BOM(應該很少公司用)是工程設計的BOM, 即將工程師畫的爆炸圖進行系統化. SAP還有幾種BOM.
標準BOM維護: CS01/CS02/CS03, 查詢CS12 銷售BOM維護: CS61/CS62/CS63, 查詢CSK2 訂單BOM維護: CO01/CO02/CO03
銷售BOM使用前提是產品必須是MAKE TO ORDER, 否則系統在展開BOM時只會拿標準BOM, 不會拿銷售BOM的數據.
標準BOM的表: MAST 銷售BOM的表: KDST
訂單BOM的表: 沒有, 我的理解就是RESB中工單需求清單
在MTO方式来说，才会产生销售订单BOM。业务部门根据客户要求，配置产生的成品特性，从而自动从标准的最大BOM中选择组件，生成销售订单BOM
这其中就明确了两个概念，销售订单BOM是在建立配置特性的基础上的，从最大化的标准BOM中选择相关特性限制的组件而产生的BOM。可以说，销售BOM是标准BOM的一个特例。这时候的标准BOM罗列了所有可能的配置。
订单BOM则是生产中使用的BOM，是MRP根据销售订单配置和标准BOM计算产生的BOM，订单BOM在下达生产之前，可以通过计划员的调整以及设置替代，更换组件或数量，而下达时依此生产的BOM。此BOM用于生产和发料，并是成本BOM的直接来源。
相关文章：
SAP 订单BOM与销售BOM的区别
订单BOM与销售BOM的区别 訂單BOM: 是實際生產時用的BOM, 在標準BOM和銷售BOM基礎上增減物料的BOM 銷售BOM: 是為特定客戶設定的BOM, 在主檔數據層次上的BOM, 在生產時是帶到訂單BOM中去的. 標準BOM: 是公司為標準生產的BOM, 在主檔數據層次上的BOM, 在生產時是帶到訂單BOM中去的…...
支付宝支付详细流程
1、二维码的生成二维码生成坐标 <!-- zxing生成二维码 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.3.3</version></dependency><dependency><groupId>co…...
TCP 的演化史-fast retransmit/recovery
工作原因要对一个 newreno 实现增加 sack 支持。尝试写了 3 天 C，同时一遍又一遍梳理 sack 标准演进。这些东西我早就了解，但涉及落地写实现，就得不断抠细节，试图写一个完备的实现。 这事有更简单的方法。根本没必要完全实现 RFC…...
CSS基础选择器，你认识多少？
前言在上一文初识CSS中，我们了解到了其格式：选择器{ }在初步尝试使用时，我们笼统的直接输入了p { }以选择p标签来对其操作，而这一章节里，我们再进一步探索有关基础选择器的相关内容，理解选择器的作用。选择…...
ChatGPT入门案例｜商务智能对话客服（三）
本篇介绍智能客服的基本功能架构和基本概念，并利用对话流技术构建商务智能应用。 01、商务智能客服功能结构 互联网的发展已经深入到社会的各个方面，智能化发展已经成为社会发展的大趋势。在大数据和互联网时代，企业和组织愈加重视客户沟通…...
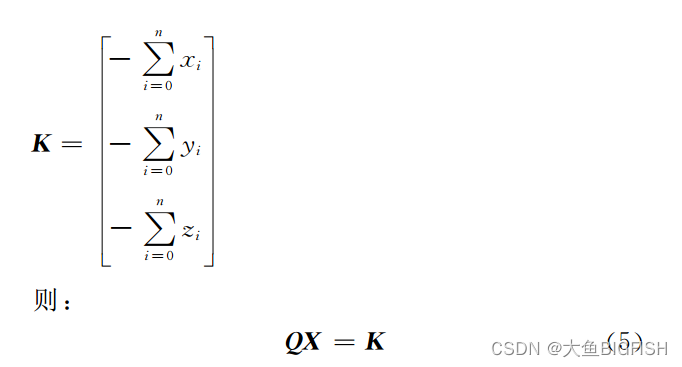
Matlab 最小二乘法拟合平面（SVD）
文章目录 一、简介1.1最小二乘法拟合平面1.2 SVD角度二、实现代码三、实现效果参考资料一、简介 1.1最小二乘法拟合平面 之前我们使用过最为经典的方式对平面进行了最小二乘拟合（点云最小二乘法拟合平面），其推导过程如下所示： 仔细观察一下可以发现...
AtCoder Regular Contest 126 D题题解
思路 首先我们看看假设选中 mmm 个数后的答案。 我们首先现将 mmm 个数移动到一起，在将他们重新排序。 我们知道，mmm 个数移在一起时，当位于中间的那个数不动时交换次数最少，于是可以列出式子（cic_ici 是点 iii 的…...
Android R WiFi热点流程浅析
Android R WiFi热点流程浅析 Android上的WiFi SoftAp功能是用户常用的功能之一，它能让我们分享手机的网络给其他设备使用。 那Android系统是如何实现SoftAp的呢，这里在FWK层面做一个简要的流程分析，供自己记录和大家参考。 以Android R版本为…...
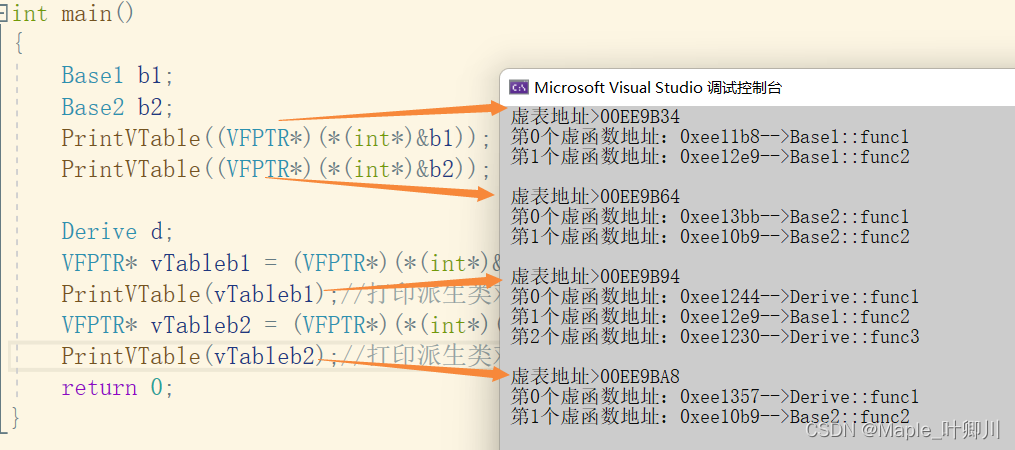
【C++进阶】二、多态详解（总）
目录 一、多态的概念 二、多态的定义及实现 2.1 多态的构成条件 2.2 虚函数 2.3 虚函数的重写 2.4 虚函数重写的两个例外 2.4.1 协变 2.4.2 析构函数的重写 2.5 C11 override 和 final 2.5.1 final 2.5.2 override 2.6 重载、覆盖(重写)、隐藏(重定义)的对比 三、…...
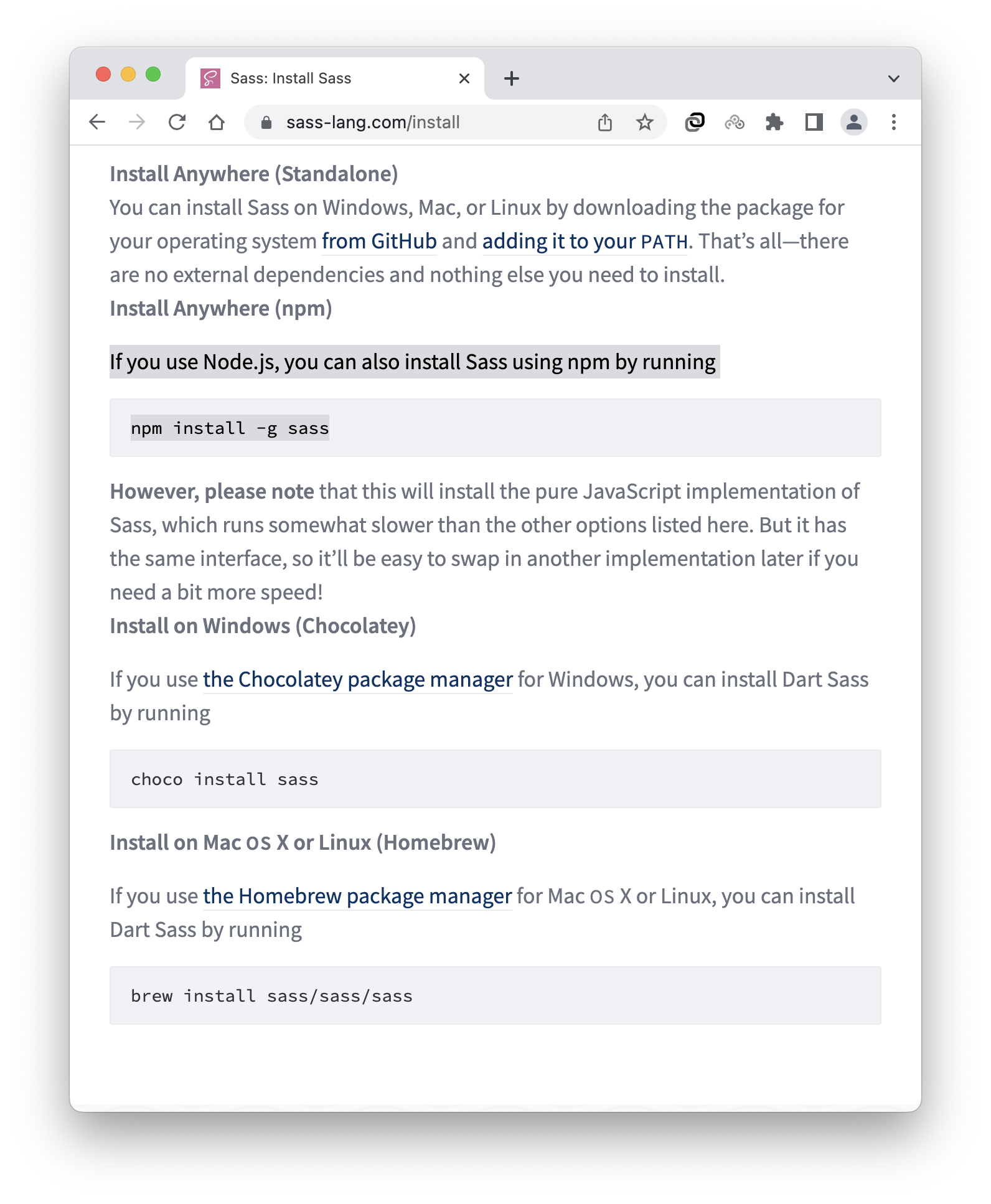
node-sass@4.14.1 包含风险， 如何升级依赖至 dart-sass
文章目录需求我上网都查到了哪些信息在 github 看到了 node-sass 依赖的最新版本的列表：关于方案2的失败不同版本的 nodejs 和 node-sass依赖的**适配关系**从何得知替代方案——dart-sass如何安装 dart sass？需求 在做一个基于Node、React的前端项目&a…...
DataWhale 大数据处理技术组队学习task2
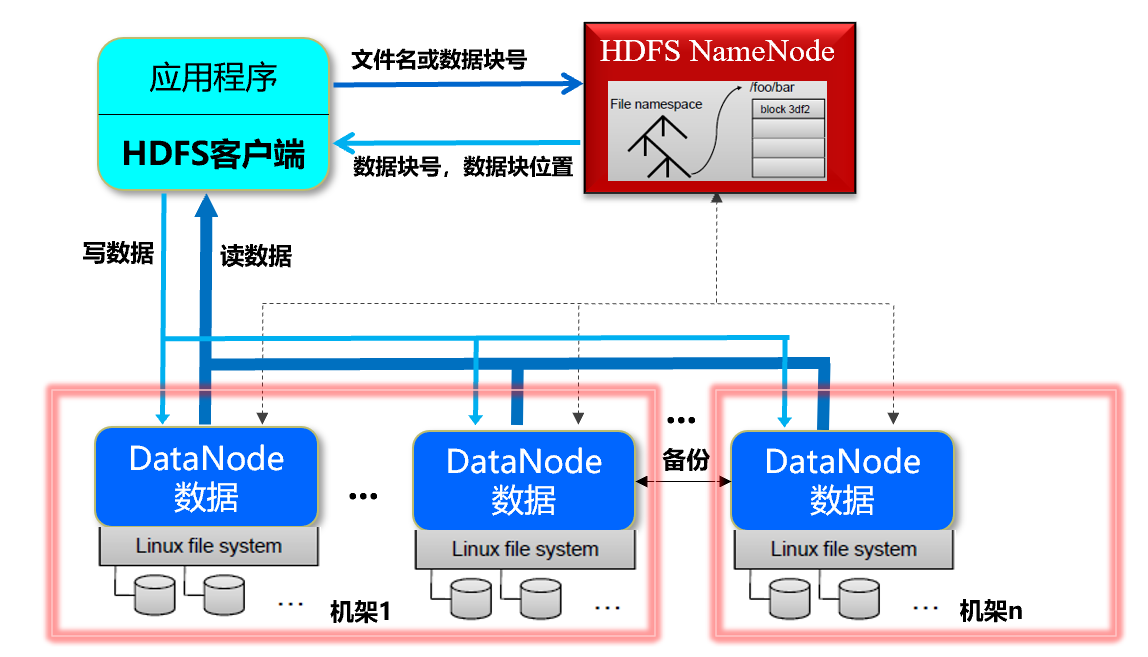
三、Hadoop分布式文件系统 1. 产生背景 数据量越来越大，一台独立的计算机已经无法存储所有的数据---->将大规模的数据存储到成百上千的计算机中------为了解决数据管理以及维护极其繁琐与低效------>分布式文件系统 分布式文件系统是管理网络中跨多台计算机…...
一文读懂select、poll、epoll的用法
select，poll，epoll都是IO多路复用的机制。I/O多路复用就通过一种机制，可以监视多个描述符，一旦某个描述符就绪（一般是读就绪或者写就绪），能够通知程序进行相应的读写操作。但select，…...
《C陷阱与缺陷》----词法“陷阱”
导言： 由于一个程序错误可以从不同层面采用不同方式进行考察，而根据程序错误与考察程序的方式之间的相关性，可以将程序错误进行划分为各种陷阱与缺陷： ①.词法“陷阱” ②.语法“陷阱” ③.语义“陷阱” ④.连接问题 ⑤.库函数问…...
千锋教育+计算机四级网络-计算机网络学习-04
UDP概述 UDP协议 面向无连接的用户数据报协议，在传输数据前不需要先建立连接；目地主机的运输层收到UDP报文后，不需要给出任何确认 UDP特点 相比TCP速度稍快些简单的请求/应答应用程序可以使用UDP对于海量数据传输不应该使用UDP广播和多播应用…...
蓝桥杯算法训练合集十四 1.P08052.P07053.同余方程4.P08015.ascii应用
目录 1.P0805 2.P0705 3.同余方程 4.P0801 5.ascii应用 1.P0805 问题描述 当两个比较大的整数相乘时，可能会出现数据溢出的情形。为避免溢出，可以采用字符串的方法来实现两个大数之间的乘法。具体来说，首先以字符串的形式输入两个整数&…...
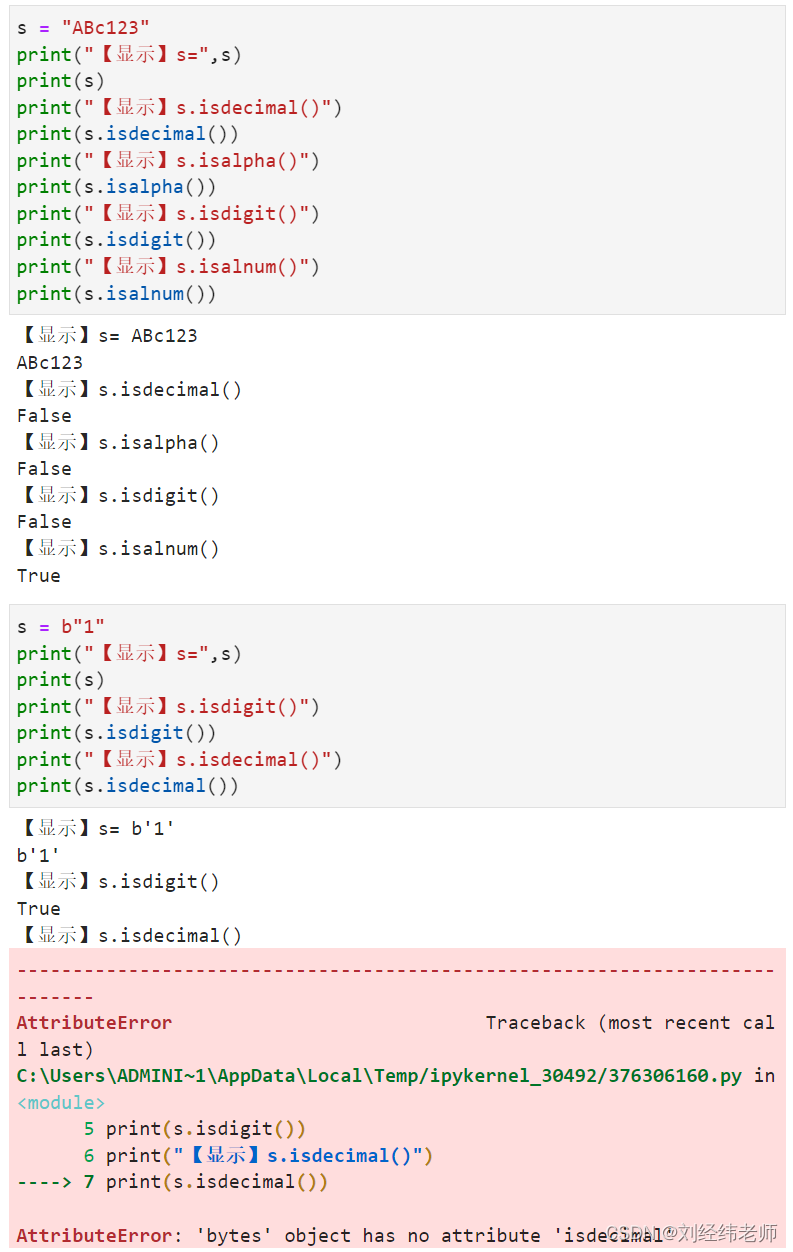
判断字符串中的字符的类型isdecimal()；isalpha()；isdigit()；isalnum()
【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 判断字符串中的字符的类型 isdecimal()；isalpha()；isdigit()；isalnum() [太阳]选择题 对于代码中isdecimal()和isalnum()输出的结果是? s "ABc123&…...
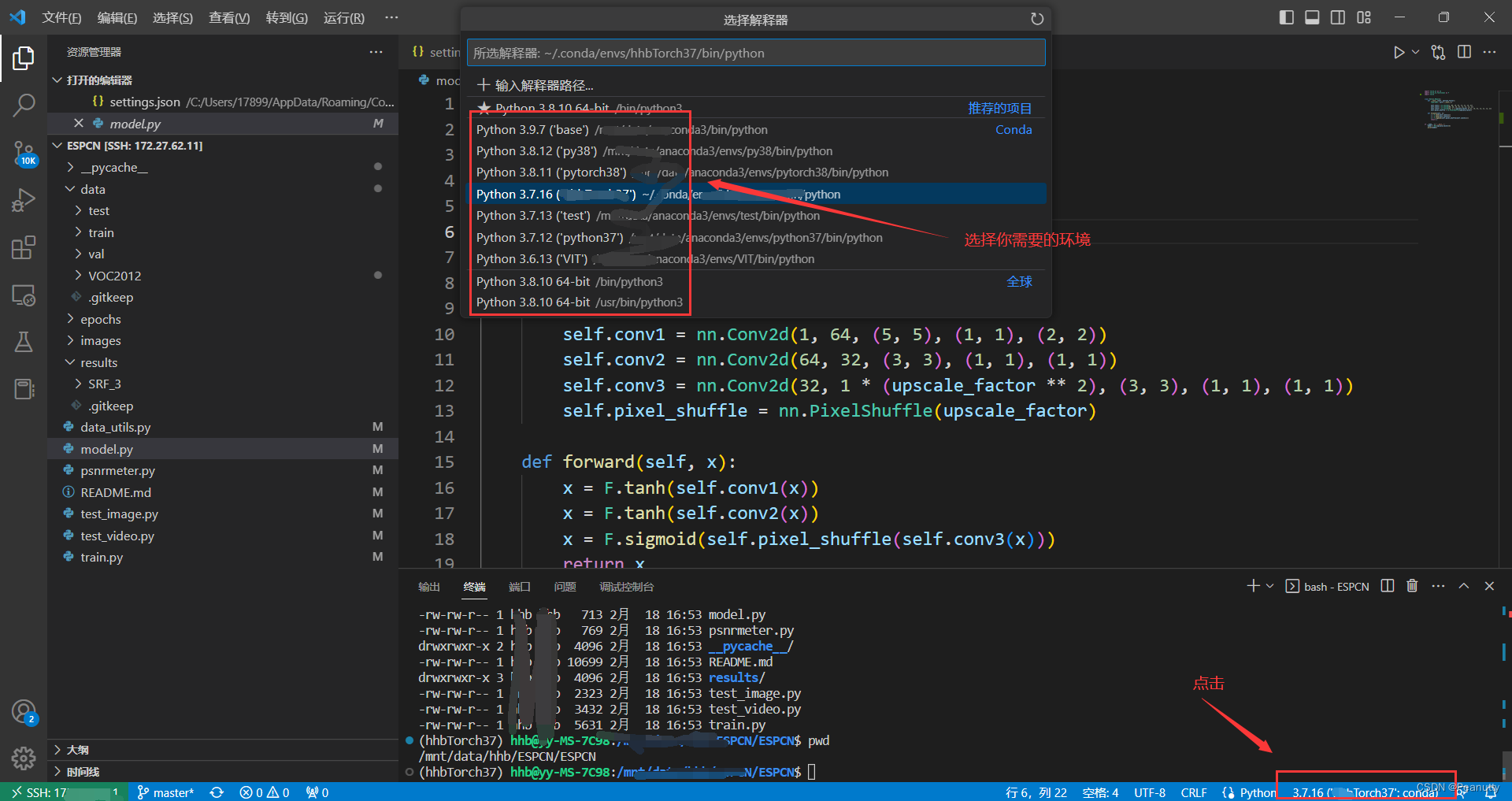
VSCode远程调试Linux代码，python解释器配置
安装插件并配置 安装后找到插件图标，点击 点击SSH上的 号 在弹出框中输入命令：ssh usernameip -p port username: 远程服务器的用户名 ip： 远程ip port：端口号，没有可以不用 输入完毕后点击enter 选择ssh配置文件保存…...
03：入门篇 - CTK Plugin Framework 基本原理
作者： 一去、二三里 个人微信号： iwaleon 微信公众号： 高效程序员 CTK Plugin Framework 技术是面向 C++ 的动态模型系统。该系统允许插件之间的松散耦合，并且提供了设计良好的方式来进行功能和数据的交互。此外，它没有预先对插件施加限制，这样就可以很容易地将插件的相关…...
面试攻略，Java 基础面试 100 问（九）
数组有没有 length()方法?String 有没有 length()方法？ 数组没有 length()方法，有 length 的属性。String 有 length()方法。JavaScript 中，获得字符串的长度是通过 length 属性得到的，这一点容易和 Java混淆。 在 Java 中&…...
JavaScript 代码不嵌套主义
文章目录前言一、何为嵌套代码二、避免嵌套1.提炼抽取2.反转排列总结前言 看过不少过度嵌套的代码, 我真正意识到问题的严重性是刚入职那会, 我在一个老项目里看到了40个连续的else if, 套了6层的if, for和forEach, 因为我们并没有做什么限制代码嵌套的提前约定. 呃, 那之后认…...
【大模型RAG】拍照搜题技术架构速览：三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道（多模态 OCR → 语义检索 → 答案渲染）、两级检索（倒排 BM25 向量 HNSW）并以大语言模型兜底”的整体框架： 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后，分别用…...
解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet，点击确认后如下提示 最终上报fail 解决方法 内核升级导致，需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...
聊聊 Pulsar：Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台，以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中，Producer（生产者） 是连接客户端应用与消息队列的第一步。生产者…...
C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj，再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一：使用Read()读取文件2.3、方式二：bufio读取文件2.4、方式三：os.ReadFile读取2.5、写…...
Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中，return 语句的使用是另一个关键概念，它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别：不同层级的事件处理 方…...
nnUNet V2修改网络——暴力替换网络为UNet++
更换前，要用nnUNet V2跑通所用数据集，证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构，初步了解要修改的网络，知己知彼，修改起来才能游刃有余。 U-Net存在两个局限，一是网络的最佳深度因应用场景而异，这取决于任务的难度和可用于训练的标注数…...
区块链技术概述
区块链技术是一种去中心化、分布式账本技术，通过密码学、共识机制和智能合约等核心组件，实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点：数据存储在网络中的多个节点（计算机），而非…...
消防一体化安全管控平台：构建消防“一张图”和APP统一管理
在城市的某个角落，一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延，滚滚浓烟弥漫开来，周围群众的生命财产安全受到严重威胁。就在这千钧一发之际，消防救援队伍迅速行动，而豪越科技消防一体化安全管控平台构建的消防“…...
门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构：由肠系膜上静脉和脾静脉汇合构成，是肝脏血液供应的主要来源。淤血后果：门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血，引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...