考研C语言进阶题库——更新6-10题
目录
6输入一个字符串,输出其中字母的个数
7用递归求函数值x=1,f(x)=10,x>1.f(x)=f(x-1)+2
8所给字符串正序反序连接,形成新串并输出
9输入若干个整数以-1标记为结束输出其中的最大值
10求矩阵的两条对角线之和
6输入一个字符串,输出其中字母的个数
//6输入一个字符串,输出其中字母的个数
#include <stdio.h>
#include <string.h>
int main(){//初始化char s[20];gets(s);int count=0;for (int i = 0; i < strlen(s); i++) {if((s[i]>='A' && s[i]<='Z') || (s[i]>='a' && s[i]<='z')){count++;}}printf("%d",count);return 0;
}7用递归求函数值x=1,f(x)=10,x>1.f(x)=f(x-1)+2
//7用递归求函数值x=1,f(x)=10,x>1.f(x)=f(x-1)+2
#include <stdio.h>int f(int number){int x;if(number==1){x=10;}else{return f(number-1)+2;}return x;
};int main(){//初始化int number;scanf("%d",&number);printf("当x=%d是,递归后的结果为:%d",number,f(number));return 0;
}8所给字符串正序反序连接,形成新串并输出
//8所给字符串正序反序连接,形成新串并输出
#include <stdio.h>
#include <string.h>
int main(){//初始化char a[22],b[11];//qwertyuiop//qwertyuioppoiuytrewqint t;gets(a);t= strlen(a)-1;// 减去换行符的长度for (int i = 0; i < strlen(a); i++, t--) {b[t]=a[i];}puts(strcat(a,b));return 0;
}9输入若干个整数以-1标记为结束输出其中的最大值
//9输入若干个整数以-1标记为结束输出其中的最大值.c
#include <stdio.h>
#include <limits.h>int main() {//初始化int number, max = INT_MIN;//无穷小//重点//while (scanf("%d", &number) != EOF && number != -1) {while (scanf("%d", &number) == 1 && number != -1) {if (number > max) {max = number;}}printf("%d", max);return 0;
}
10求矩阵的两条对角线之和
//10求矩阵的两条对角线之和
#include <stdio.h>int main(){//初始化int length,t,sum=0;scanf("%d",&length);int arr[length][length];//要放在下面for (int i = 0; i < length; i++) {for (int j = 0; j < length; j++) {scanf("%d",&t);arr[i][j]= t;if(i==j || i==(length-1)-j){sum+=arr[i][j];}}}printf("%d",sum);return 0;
}相关文章:

考研C语言进阶题库——更新6-10题
目录 6输入一个字符串,输出其中字母的个数 7用递归求函数值x1,f(x)10,x>1.f(x)f(x-1)2 8所给字符串正序反序连接,形成新串并输出 9输入若干个整数以-1标记为结束输出其中的最大值 10求矩阵的两条对角线之和 6输入一个字符串,输出其中…...

汽车BOOTLOADER开发经历
鄙人参与电动汽车BOOTLOADER开发近三年,从完全没有这方面的基础到参与国内外大小知名或不知名车企的电动车三大件的BOOTLOADER开发,总结了以下一点学习心得。 1.熟悉基本术语含义 诊断、寻址方式、FBL、擦除、驱动 2.熟悉国际标准、UDS服务格式 汽车的…...

适配器模式(C++)
定义 将一个类的接口转换成客户希望的另一个接口。Adapter模式使得原本由于接口不兼容而不能一起工作的那些类可以一起工作。 应用场景 在软件系统中,由于应用环境的变化,常常需要将“一些现存的对象 ”放在新的环境中应用,但是新环境要求…...

HTTP连接之出现400 Bad Request分析
1、400简介 400是一种HTTP状态码,告诉客户端它发送了一条异常请求。400页面是当用户在打开网页时,返回给用户界面带有400提示符的页面。其含义是你访问的页面域名不存在或者请求错误。主要分为两种。 1、语义有误,当前请求无法被服务器理解…...

后端开发, 接口幂等性是什么意思
在后端开发中,接口的幂等性是指同一个请求的多次执行所产生的效果与执行一次的效果相同。简而言之,对于同一个接口请求,无论发送多少次,其对资源的状态修改结果都是一致的。 幂等性在接口设计和实现中非常重要,特别是在涉及数据修改或资源状态变更的情况下。如果一个接口…...
k8s手动发布镜像的方法
kubectl edit deploy编辑对应的文件,并:wq!保存即可...

十二、ESP32控制步进电机
1. 运行效果 2. 步进电机 最大特点:能够控制旋转一定的角度 3. 步进电机原理...
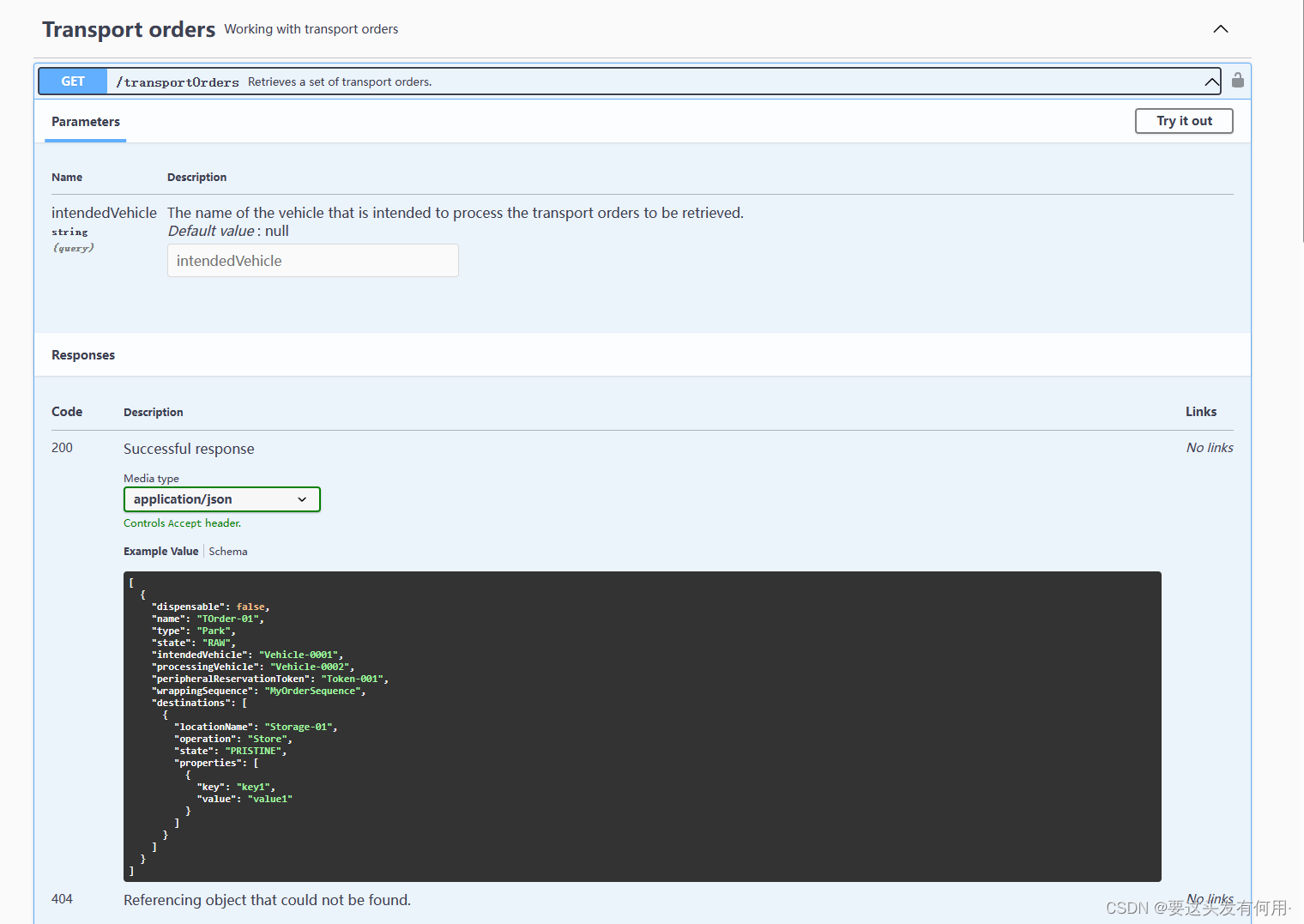
利用openTCS实现车辆调度系统(六)openTCS订单的使用
运输订单 由类的实例表示,描述了由车辆执行的进程。 通常,此过程是货物从一个地点到另一个地点的实际运输。 然而,A也可以只描述车辆到目的地位置的运动以及要执行的可选车辆操作。TransportOrderTransportOrder 以下所有内容都是 openTCS …...

第一天 什么是CSRF ?
✅作者简介:大家好,我是Cisyam,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Cisyam-Shark的博客 💞当前专栏: 每天一个知识点 ✨特色专…...

知识图谱推荐系统研究综述
基于协同过滤的推荐是当前应用最为广泛的推荐方法,但也存在着新用户或新项目的冷启动以及数据稀疏等问题。针对上述两种方法出现的问题,研究者进一步提出了混合推荐系统。混合推荐系统结合上述两种方法的优点,可以有效缓解其中的不足,增加推荐的准确性。但是,混合推荐系统…...

基于Centos7的Nginx源码安装
目录 1、准备安装环境 2、获取tar包: 3、解压创建软链接 4、创建用户和组 5、执行安装 6、创建服务脚本 7、开启nginx:编辑编辑 1、准备安装环境 yum insatall -y make gcc gcc-c pcre-devel #pcre-devel -- pcre库 #安装openssl-devel yum …...
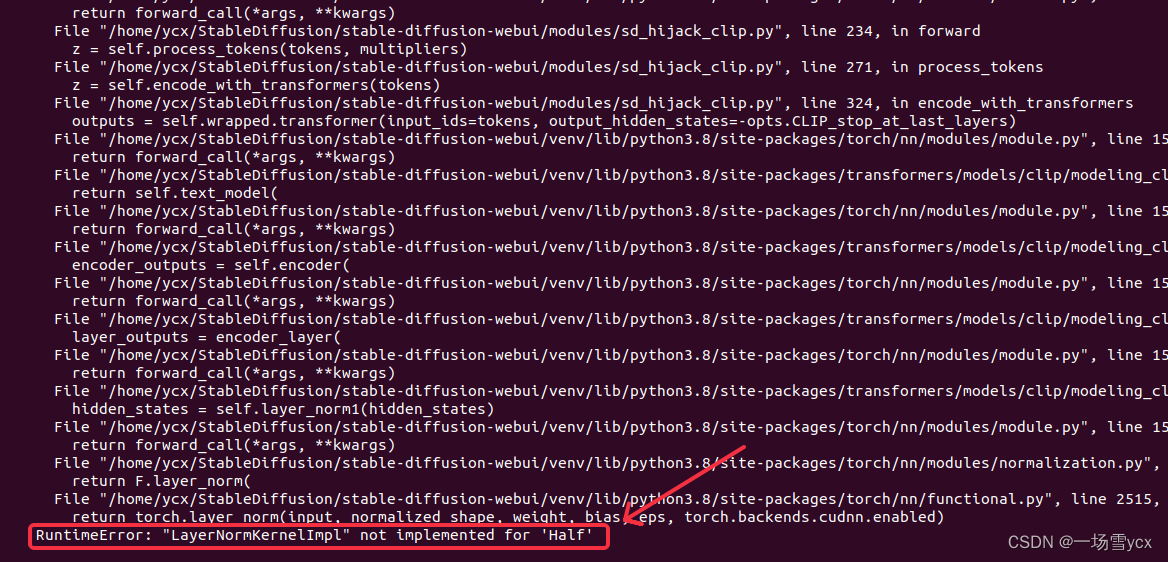
Ubuntu 20.04 安装 Stable Diffusionn
步骤 1:安装 wget、git、Python3 和 Python3虚拟环境(如果已安装可忽略这步骤) sudo apt install wget git python3 python3-venv步骤 2:克隆 SD 项目到本地 git clone https://github.com/AUTOMATIC1111/stable-diffusion-webu…...

vue name命名错误 Do not use built-in or reserved HTML elements as component
描述: Do not use built-in or reserved HTML elements as component id: header 这里指的是components的名称命名不正确。 在项目中我使用的是header 作为组件名称,但是在前端html中这个是内置组件来的,名称已被占用不能再使用这些名称了。…...

知识付费系统开发:构建高效智能的付费内容平台
随着数字化时代的来临,知识付费正迅速崭露头角,为知识创作者和求知者带来了全新的商机。在这个背景下,开发一款高效智能的知识付费系统成为了一项重要的任务。本文将深入探讨如何基于Python编程语言和相关技术构建一个智能的知识付费内容平台…...

数据结构----结构--线性结构--递归
数据结构----结构–线性结构–递归 1.递归的概念 递归:将一个问题拆解成解决方案完全相同的子问题,并且有一个明确的终点 看如下递归代码理解一下递归 void fun(int n){if(n4){printf("%d",n);return;}fun(n1);printf("%d",n); …...

在Windows批处理程序中实现延时功能
方法1:使用PowerShell echo off:: 使用 PowerShell 的 Start-Sleep 命令来实现精确延时 powershell -command "Start-Sleep -Milliseconds 3000"echo Delay complete. 不过,通常Win7专业版和旗舰版中都会默认安装了PowerShell,但是标准版和家…...
Java基础入门篇——Java变量类型的转换和运算符(七)
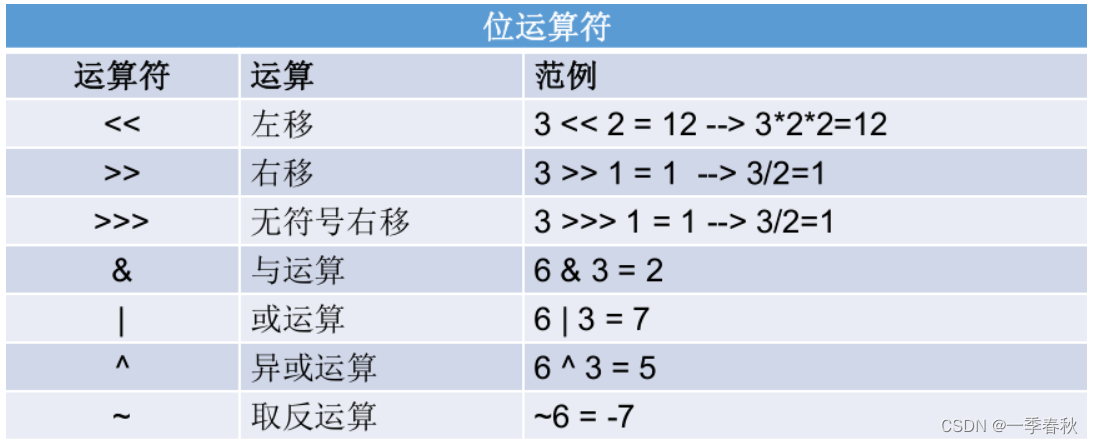
目录 一、变量类型 1.1自动类型转换(隐式转换) 1.2 强制类型转换(显式转换) 1.3类型转换的其他情况 二、运算符 2.1算术运算符 2.2比较运算符 2.3逻辑运算符 2.4位运算符 三、总结 在Java中,变量类型的转换…...
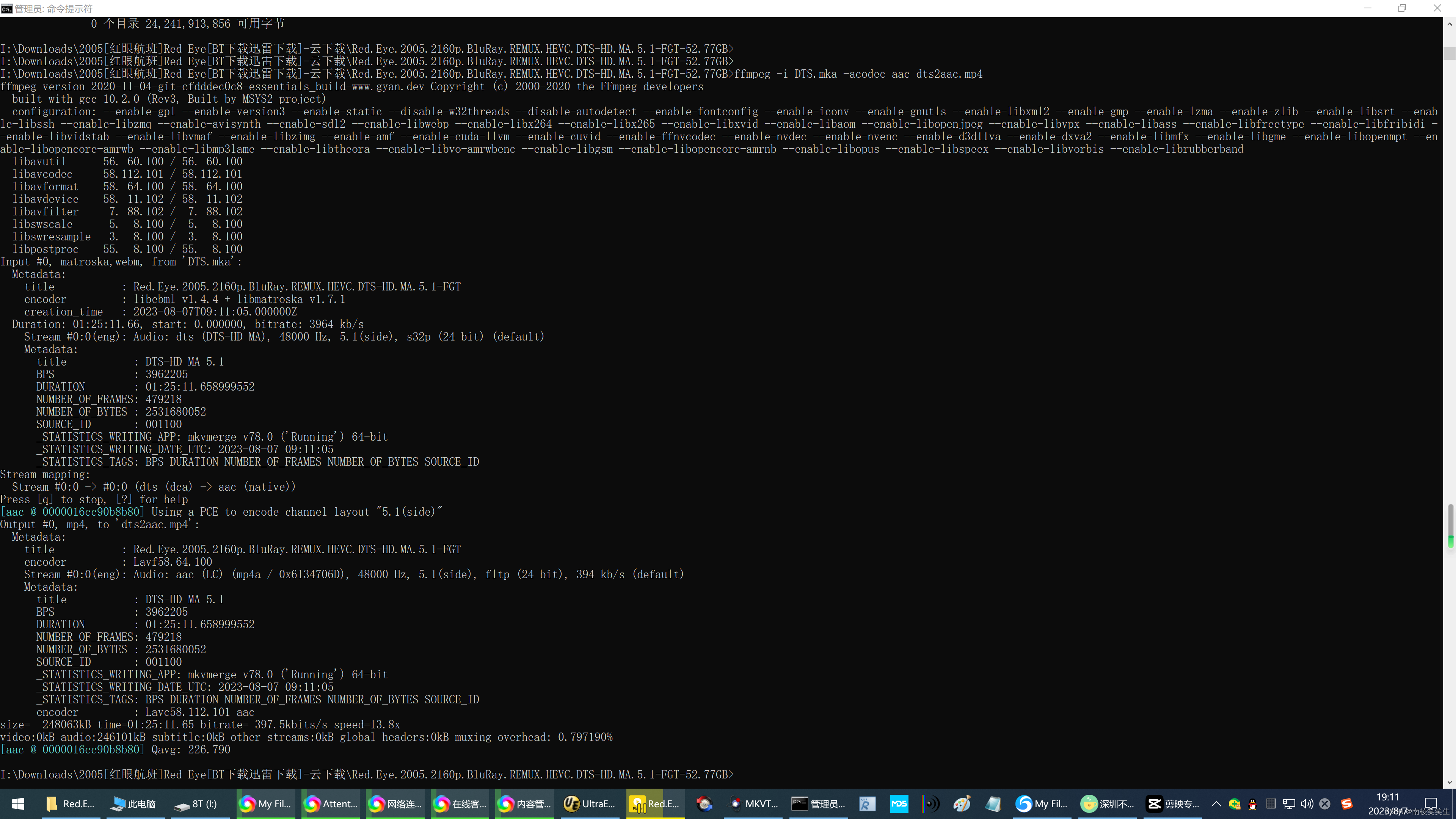
20230807通过ffmpeg将DTS编码的AUDIO音频转换为AAC编码
20230807通过ffmpeg将DTS编码的AUDIO音频转换为AAC编码 2023/8/7 20:04 ffmpeg dts 转AAC 缘起:由于网上找的电影没有中文字幕,有内置的英文字幕,但是还是通过剪映/RP2023识别一份英文字幕备用! I:\Downloads\2005[红眼航班]Red E…...
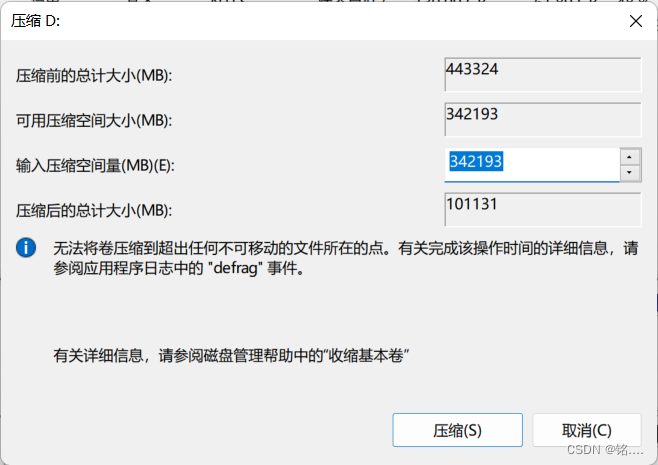
一生一芯1——windows与Ubuntu双系统安装
UltraISO下载 下载链接:https://pan.baidu.com/s/18ukDs6yL64qU6thYyZEo-Q?pwdo8he 提取码:o8he 一路傻瓜安装,安装后点击继续试用 Ubuntu系统下载 这里我使用的是官网的22.04版本,由于大于4G,无法上传至百度网盘…...

Linux下的CGI服务器
一、概述 使用进程池,半同步/半异步并发模式。 同步进程:工作子进程负责进行具体的连接以及具体的I/O,顺序执行 异步进程:主进程监听连接事件,将连接任务分发给子线程 二、设计逻辑 1.设计进程池的创建逻辑 2.父…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
