数据结构----结构--线性结构--递归
数据结构----结构–线性结构–递归
1.递归的概念
递归:将一个问题拆解成解决方案完全相同的子问题,并且有一个明确的终点
看如下递归代码理解一下递归
void fun(int n){if(n==4){printf("%d",n);return;}fun(n+1);printf("%d",n);
}int main(){int a=1;fun(a);//输出的结果为 4 3 2 1
}
二.斐波那契数列
1.用递归实现斐波那契数列
int Fib(int n) {if(n==0) return;if (n==1||n==2) {return 1;}return Fib(n - 1)+ Fib(n - 2);}
优化
保存已经算过的递归结果
时间复杂度O(n)
空间复杂度O(递归的深度)
2.用循环实现斐波那契数列
int Fib(int n) {if (n == 0) return;if (n == 1 || n == 2) {return 1;}int a = 1;//n-2int b = 1;//n-1int c = 0;//nfor (int i = 3; i <= n; i++) {c = a + b;a = b;b = c;}return c;
}
时间复杂度O(n)
空间复杂度O(1)
3.青蛙跳台阶问题(网址https://leetcode.cn/problems/qing-wa-tiao-tai-jie-wen-ti-lcof/)
题目:
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
分析:
这道题就是斐波那契数列的变形
每一次都可以选择跳1级还是2级,
拿三阶台阶来说 它的总方法就是跳二阶台阶的方法加上跳一阶台阶方法 F(3)=F(2)+F(1)
拿四阶台阶来说 它的总方法就是跳三阶台阶的方法加上跳二阶台阶方法 F(4)=F(3)+F(2)
依次类推
F(n)=F(n-1)+F(n-2)
这里注意F(1)=1 ,F(2)=2
代码为
//这里的代码是c语言下的
int numWays(int n) {if (n == 1 || n == 0) {return 1 % (1000000007);}if (n == 2) {return 2 % (1000000007);}int a = 1;//n-2 台阶的方法int b = 2;//n-1 台阶的方法int c=0;//n 台阶的方法for (int i = 3; i <= n; i++) {c = (a + b)% 1000000007;a = b% 1000000007;b = c% 1000000007;}return c % 1000000007;
}相关文章:

数据结构----结构--线性结构--递归
数据结构----结构–线性结构–递归 1.递归的概念 递归:将一个问题拆解成解决方案完全相同的子问题,并且有一个明确的终点 看如下递归代码理解一下递归 void fun(int n){if(n4){printf("%d",n);return;}fun(n1);printf("%d",n); …...

在Windows批处理程序中实现延时功能
方法1:使用PowerShell echo off:: 使用 PowerShell 的 Start-Sleep 命令来实现精确延时 powershell -command "Start-Sleep -Milliseconds 3000"echo Delay complete. 不过,通常Win7专业版和旗舰版中都会默认安装了PowerShell,但是标准版和家…...
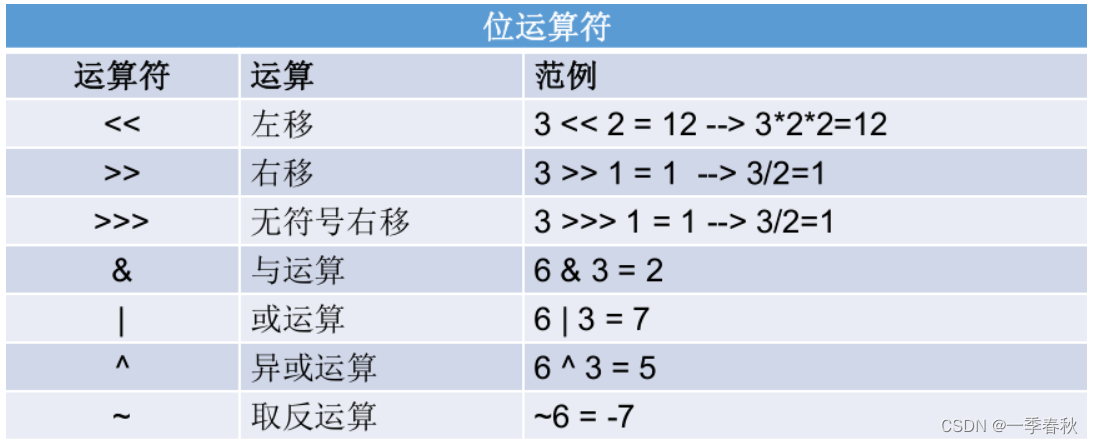
Java基础入门篇——Java变量类型的转换和运算符(七)
目录 一、变量类型 1.1自动类型转换(隐式转换) 1.2 强制类型转换(显式转换) 1.3类型转换的其他情况 二、运算符 2.1算术运算符 2.2比较运算符 2.3逻辑运算符 2.4位运算符 三、总结 在Java中,变量类型的转换…...
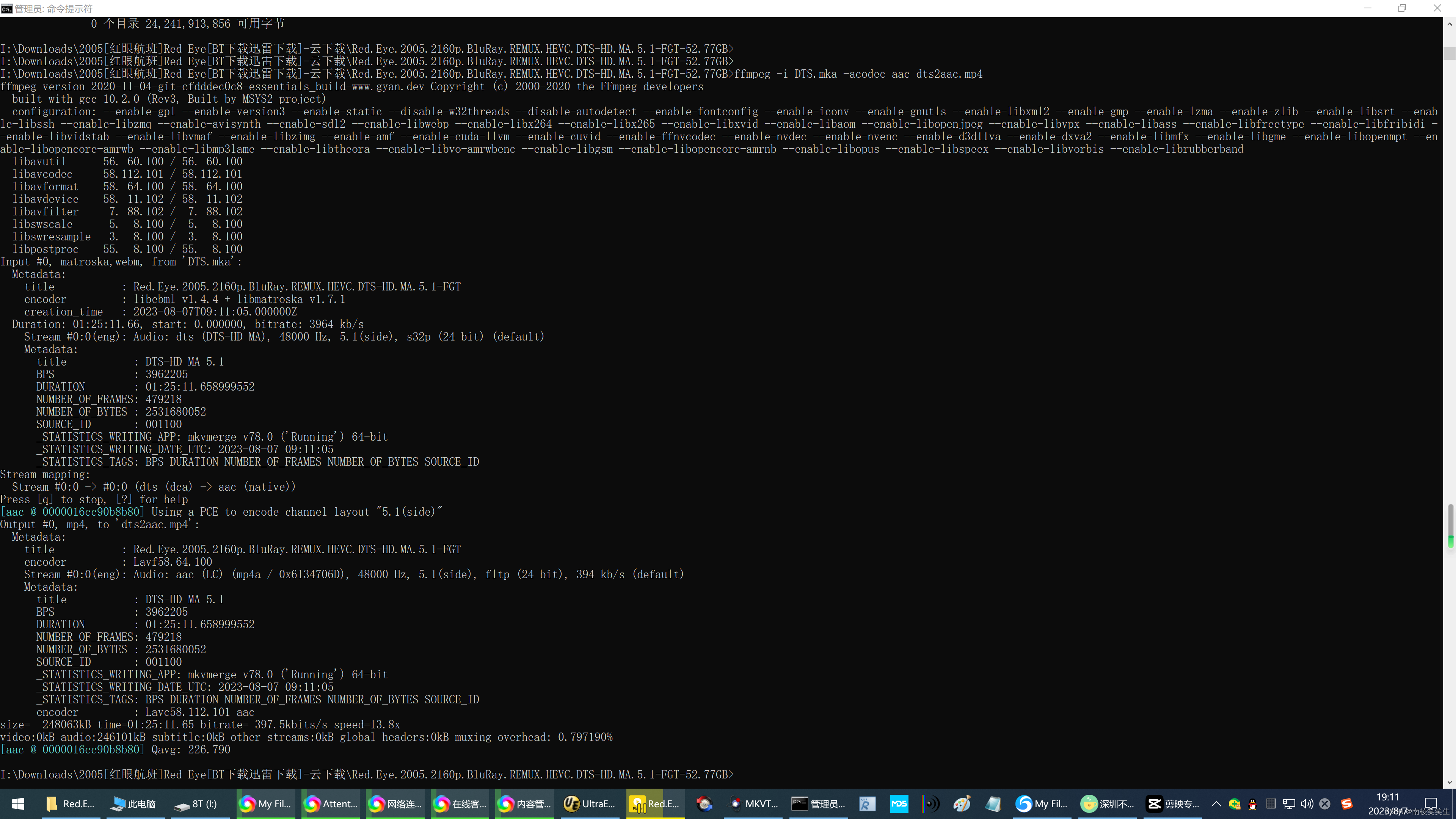
20230807通过ffmpeg将DTS编码的AUDIO音频转换为AAC编码
20230807通过ffmpeg将DTS编码的AUDIO音频转换为AAC编码 2023/8/7 20:04 ffmpeg dts 转AAC 缘起:由于网上找的电影没有中文字幕,有内置的英文字幕,但是还是通过剪映/RP2023识别一份英文字幕备用! I:\Downloads\2005[红眼航班]Red E…...
一生一芯1——windows与Ubuntu双系统安装
UltraISO下载 下载链接:https://pan.baidu.com/s/18ukDs6yL64qU6thYyZEo-Q?pwdo8he 提取码:o8he 一路傻瓜安装,安装后点击继续试用 Ubuntu系统下载 这里我使用的是官网的22.04版本,由于大于4G,无法上传至百度网盘…...

Linux下的CGI服务器
一、概述 使用进程池,半同步/半异步并发模式。 同步进程:工作子进程负责进行具体的连接以及具体的I/O,顺序执行 异步进程:主进程监听连接事件,将连接任务分发给子线程 二、设计逻辑 1.设计进程池的创建逻辑 2.父…...

后端开发3.Fastdfs的搭建
使用Docker安装 拉取镜像 docker pull registry.cn-beijing.aliyuncs.com/tianzuo/fastdfs 启动容器(修改ip)【fastdfs/自启动】(22122/23000/8888) docker run -d --restart=always --privileged=true --net=host --name=fastdfs -e IP=你的ip地址 -e WEB_PORT=8888 -v …...
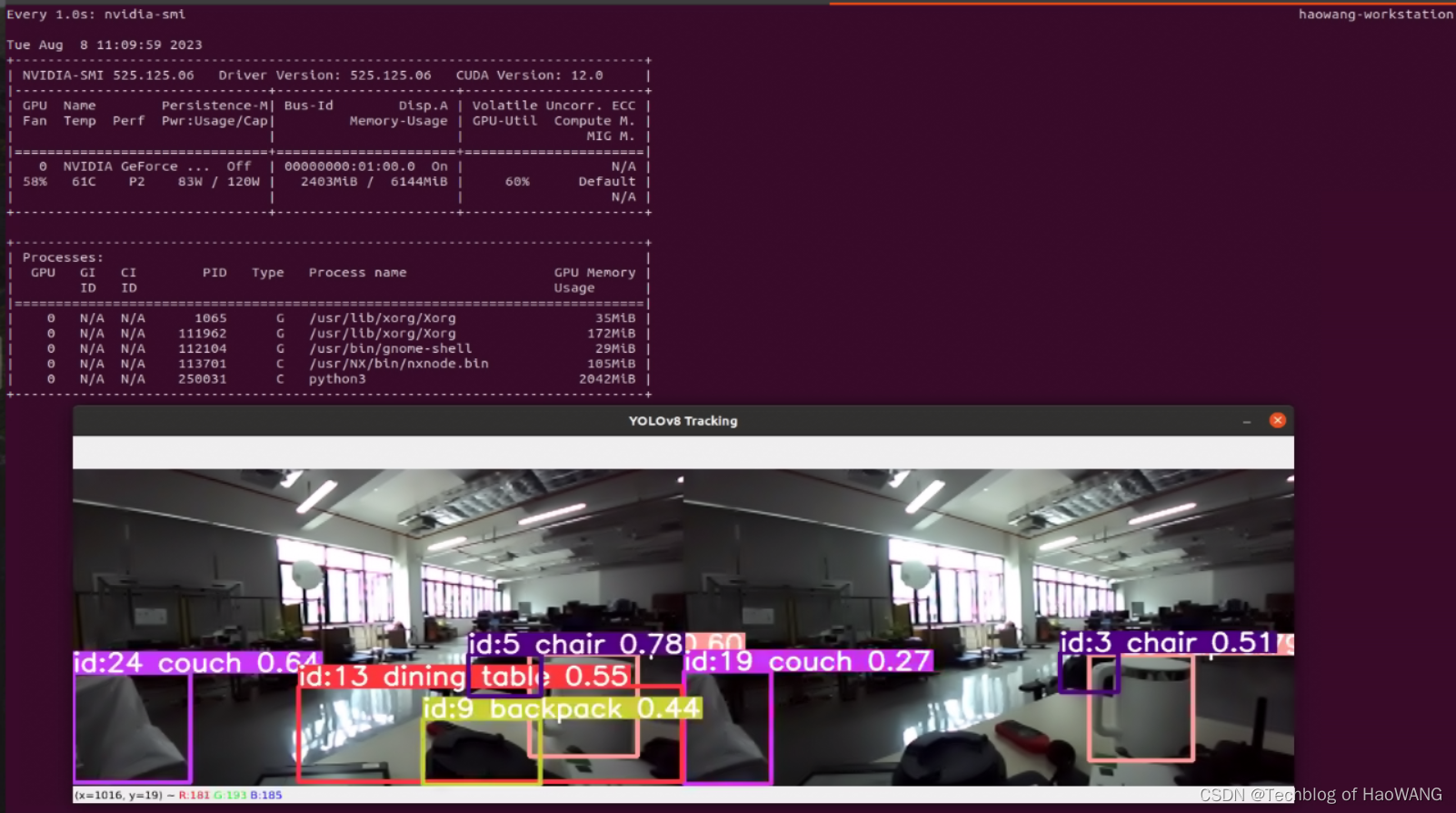
目标检测与跟踪 (3)- TensorRTYOLO V8性能优化与部署测试
系列文章目录 目标检测与跟踪 (1)- 机器人视觉与YOLO V8_Techblog of HaoWANG的博客-CSDN博客 目标检测与跟踪 (2)- YOLO V8配置与测试_Techblog of HaoWANG的博客-CSDN博客 目录 系列文章目录 前言 YOLO v8 TensorRT 一、…...
SAS-数据集SQL垂直(纵向)合并
一、SQL垂直合并的基本语法 一个selectt对应一个表,select之间用set-operator连接,set-operator包括:except(期望)、intersect(相交)、union(合并),outer un…...
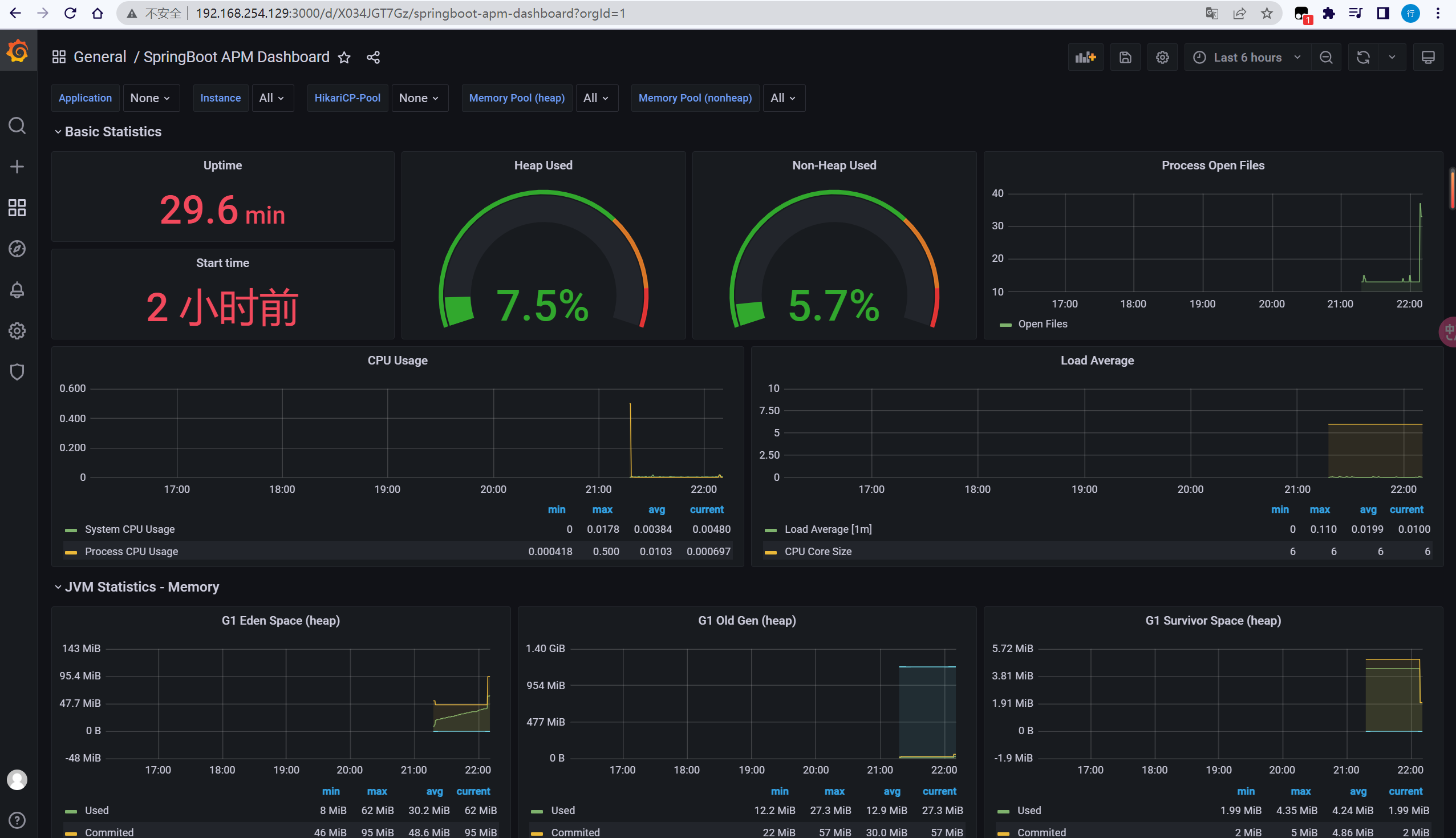
SpringBoot3 整合Prometheus + Grafana
通过Prometheus Grafana对线上应用进行观测、监控、预警… 健康状况【组件状态、存活状态】Health运行指标【cpu、内存、垃圾回收、吞吐量、响应成功率…】Metrics… 1. SpringBoot Actuator 1. 基本使用 1. 场景引入 <dependency><groupId>org.springframew…...
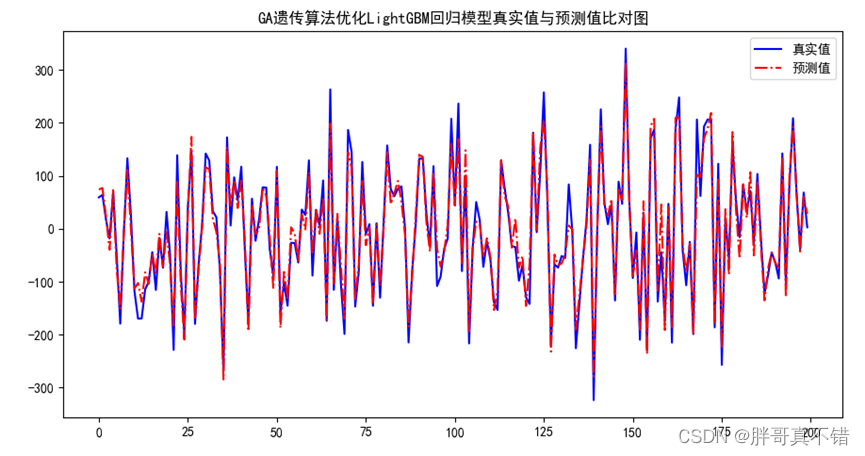
Python实现GA遗传算法优化LightGBM回归模型(LGBMRegressor算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世…...
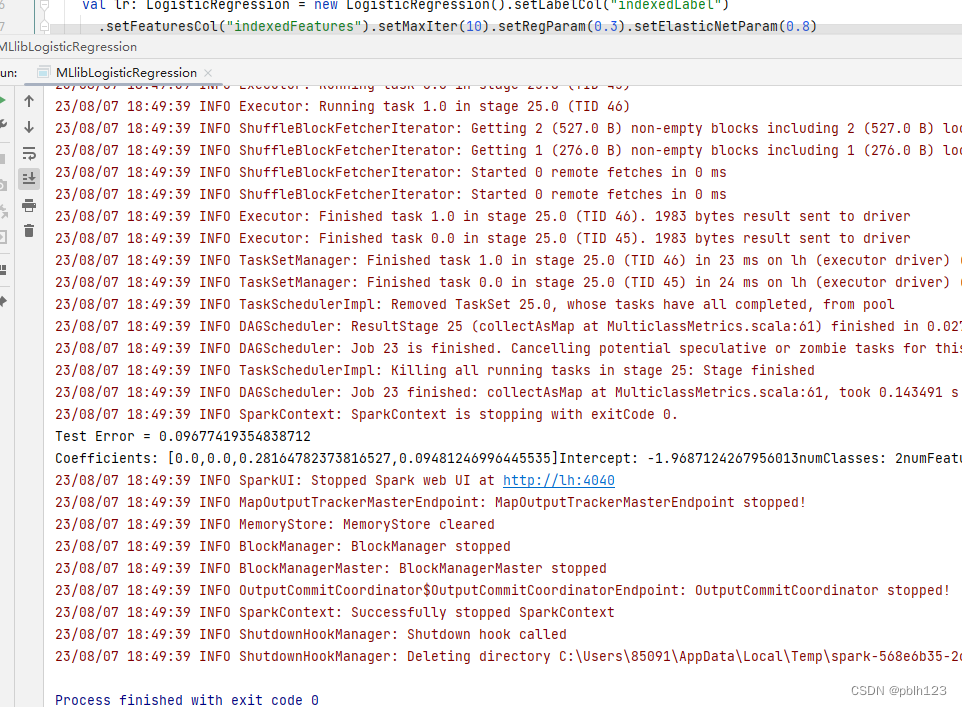
【基于IDEA + Spark 3.4.1 + sbt 1.9.3 + Spark MLlib 构建逻辑回归鸢尾花分类预测模型】
逻辑回归进行鸢尾花分类的案例 背景说明: 基于IDEA Spark 3.4.1 sbt 1.9.3 Spark MLlib 构建逻辑回归鸢尾花分类预测模型,这是一个分类模型案例,通过该案例,可以快速了解Spark MLlib分类预测模型的使用方法。 依赖 ThisBui…...
资深测试老鸟整理,性能测试-常见调优详细,卷起来...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 常见的一些性能缺…...
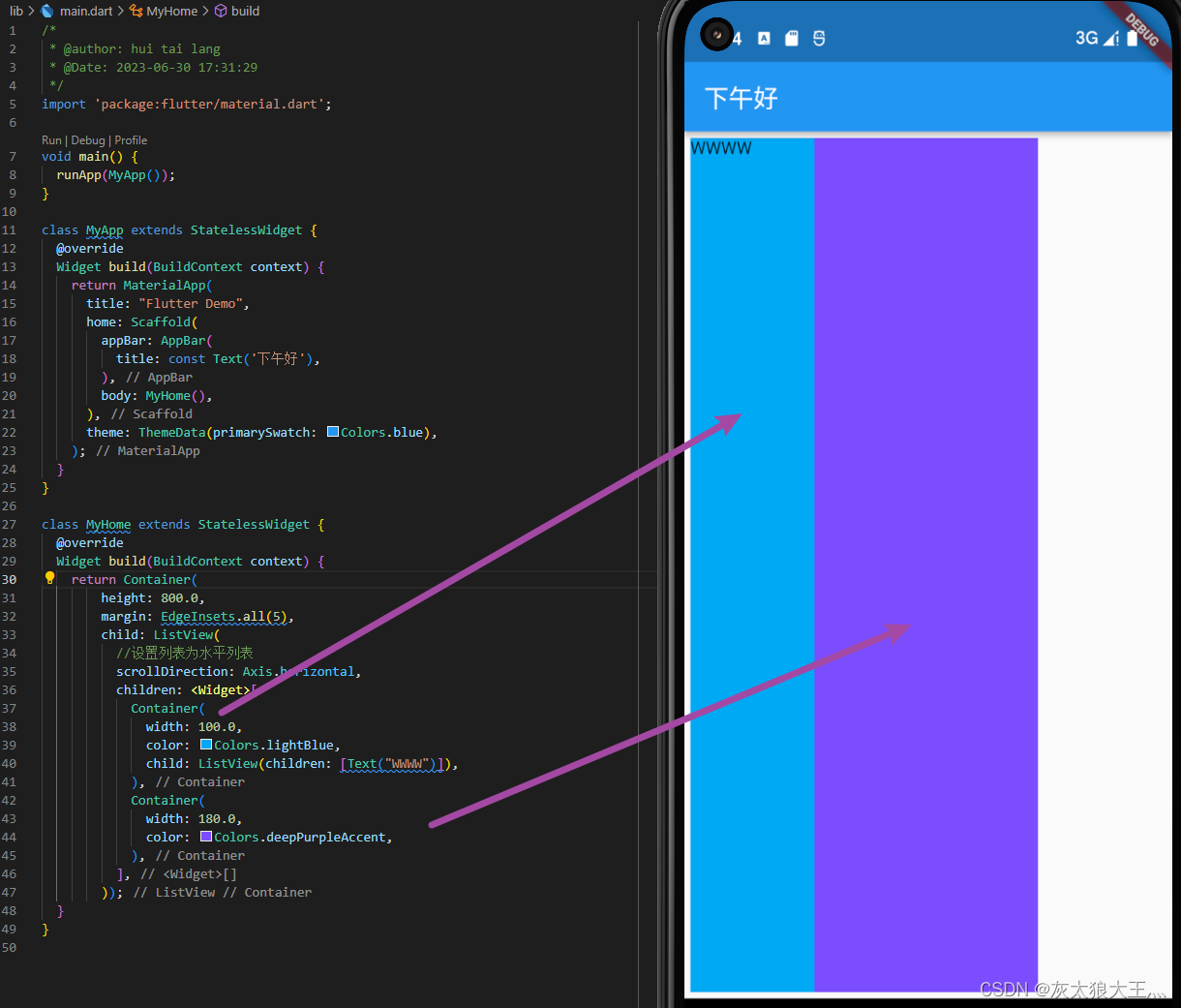
【第五章 flutter学习之flutter进阶组件-上篇】
文章目录 一、列表组件1.常规列表2.动态列表 二、FridView组件三、Stack层叠组件四、AspectRatio Card CircleAvatar组件五、按钮组件六、Stack组件七、Wrap组件八、StatefulWidget有状态组件总结 一、列表组件 1.常规列表 children: const <Widget>[ListTile(leading: …...

鸿蒙边缘计算网关正式开售
IDO-IPC3528鸿蒙边缘计算网关基于RK3568研发设计,采用22nm先进工艺制程,四核A55 CPU,主频高达2.0GHz,支持高达8GB高速LPDDR4,1T算力NPU,4K H.265/H264硬解码;视频输出接口HDMI2.0,双…...

Bytebase 2.5.0 - VCS 集成支持 Azure DevOps,支持达梦数据库
🚀 新功能 VCS 集成支持 Azure DevOps。研发版本支持达梦数据库。允许用户设置需要重新登录的频率。支持选择并导出数据库变更历史。新增 MySQL Schema 设计器。支持字段模板库。 🎄 改进 在 SQL 编辑器中,优化 MongoDB 的查询结果。优化 …...

tomcat通过systemctl启动时报错Cannot find /usr/local/tomcat/bin/setclasspath.sh
解决方法,检查自己的CATALINA_HOME和TOMCAT_HOME配置情况 我的配置在/etc/profile下的如下 使其立即生效 后将/usr/lib/systemd/system/tomcat.service中的CATALINA_HOME和TOMCAT_HOME和/etc/profile改一致 重新加载再重启解决 解决方法,检查自己的C…...
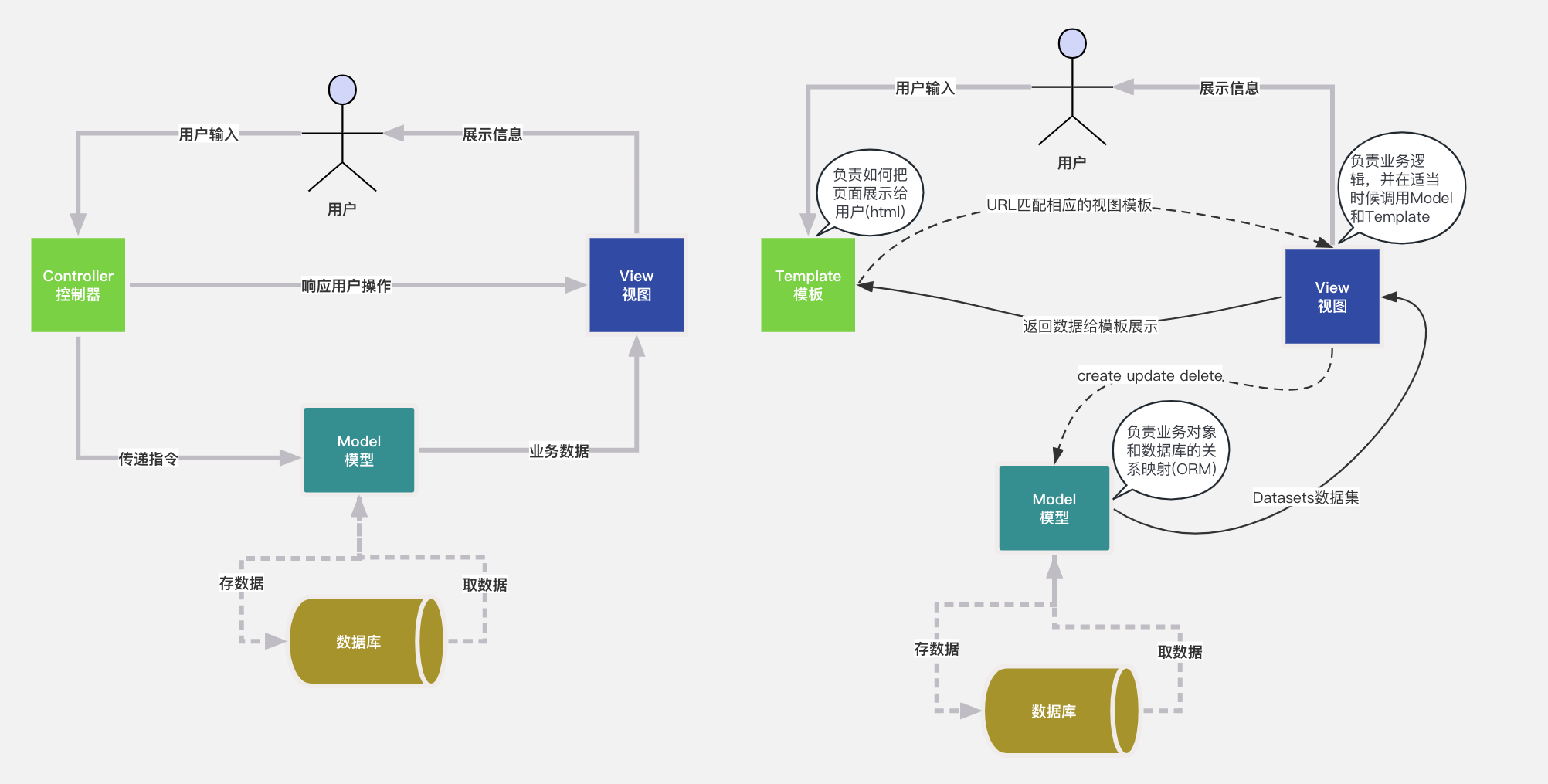
Django架构图
1. Django 简介 基本介绍 Django 是一个由 Python 编写的一个开放源代码的 Web 应用框架 使用 Django,只要很少的代码,Python 的程序开发人员就可以轻松地完成一个正式网站所需要的大部分内容,并进一步开发出全功能的 Web 服务 Django 本身…...
vue- 创建wms-web项目
vue 发展历程 安装vite 第一步 创建wms-web项目 第二步 打开文件夹并安装所有开发环境的依赖 都可以放静态资源 public>vite.svg 不会重新编译成其他名字 assets>vue.svg 会重新编译成一个随机的名称 重新编译 启动 第三步 spa 单页渲染 第四步 安装路由 第五步 …...
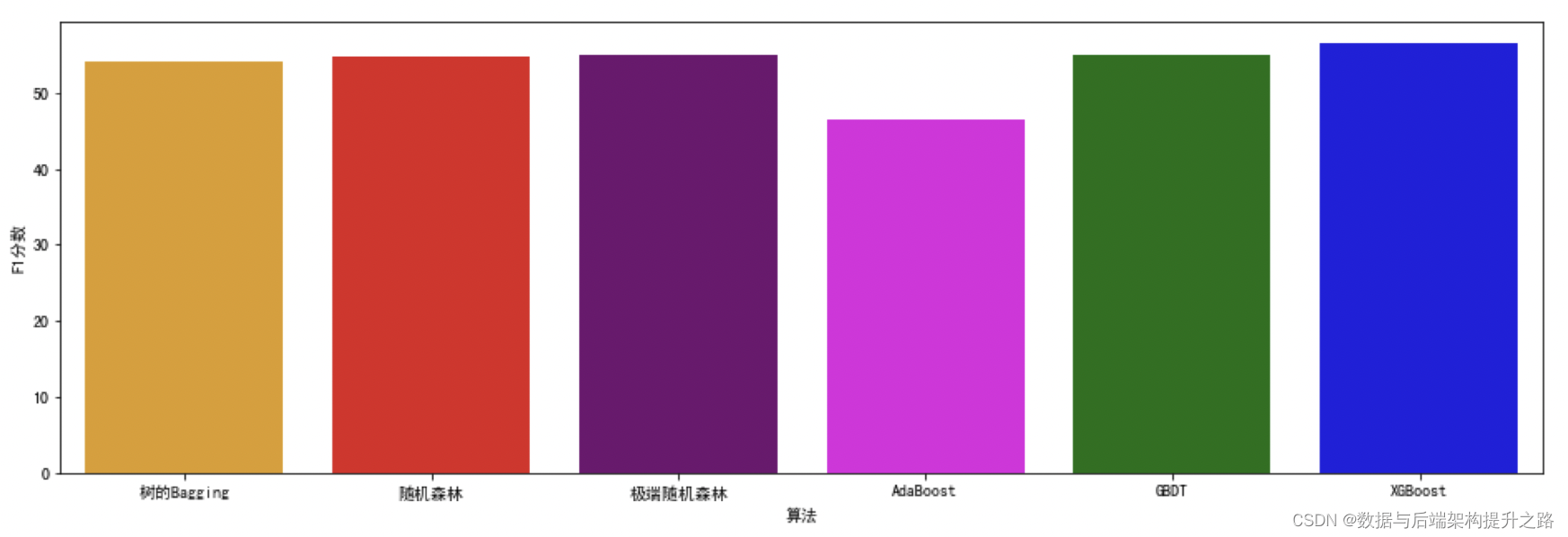
集成学习:机器学习模型如何“博采众长”
前置概念 偏差 指模型的预测值与真实值之间的差异,它反映了模型的拟合能力。 方差 指模型在不同的训练集上产生的预测结果的差异,它反映了模型的稳定性。 方差和偏差对预测结果所造成的影响 在机器学习中,我们通常希望模型的偏差和方差都…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
