mac安装open3d时候出现错误
在测试open3d是否正常顺利安装时，出现了如下错误：
python -c "import open3d as o3d; print(o3d.__version__)"
Traceback (most recent call last):File "<string>", line 1, in <module>File "/Users/huangzhe/miniconda3/envs/open3d/lib/python3.8/site-packages/open3d/__init__.py", line 93, in <module>from open3d.cpu.pybind import (core, camera, data, geometry, io, pipelines,
ImportError: dlopen(/Users/huangzhe/miniconda3/envs/open3d/lib/python3.8/site-packages/open3d/cpu/pybind.cpython-38-darwin.so, 0x0002): Library not loaded: /opt/homebrew/opt/libomp/lib/libomp.dylibReferenced from: <A2C68595-9594-3758-BEFB-86BA2C701093> /Users/huangzhe/miniconda3/envs/open3d/lib/python3.8/site-packages/open3d/cpu/pybind.cpython-38-darwin.soReason: tried: '/opt/homebrew/opt/libomp/lib/libomp.dylib' (no such file), '/System/Volumes/Preboot/Cryptexes/OS/opt/homebrew/opt/libomp/lib/libomp.dylib' (no such file), '/opt/homebrew/opt/libomp/lib/libomp.dylib' (no such file), '/usr/local/lib/libomp.dylib' (no such file), '/usr/lib/libomp.dylib' (no such file, not in dyld cache)
解决方法是运行如下命令：
brew install --build-from-source libomp
问题即可解决，再运行测试open3d版本号的命令：
python3 -c "import open3d as o3d; print(o3d.__version__)"
即可显示版本号：
相关文章：
mac安装open3d时候出现错误
在测试open3d是否正常顺利安装时，出现了如下错误： python -c "import open3d as o3d; print(o3d.__version__)" Traceback (most recent call last):File "<string>", line 1, in <module>File "/Users/huangzhe/…...
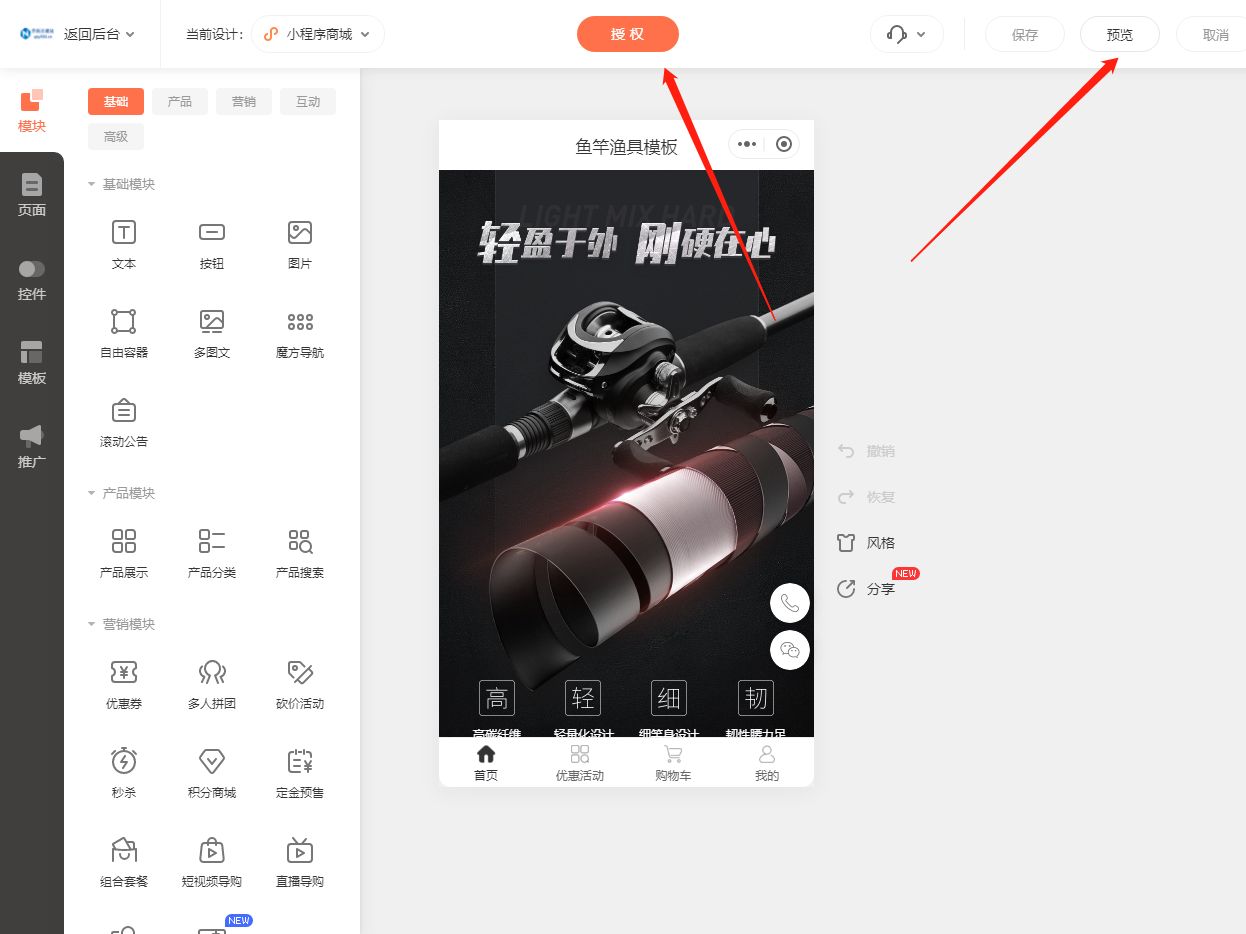
打造本地户外装备小程序商城教程大揭秘
在如今的移动互联网时代，小程序已经成为了各行各业的发展利器。尤其对于户外用具行业来说，一个专属的小程序商城将能够极大地提升企业的品牌形象和销售业绩。下面就来介绍一下快速上手制作户外用具小程序的攻略吧。 首先，登录乔拓云平台进入商…...
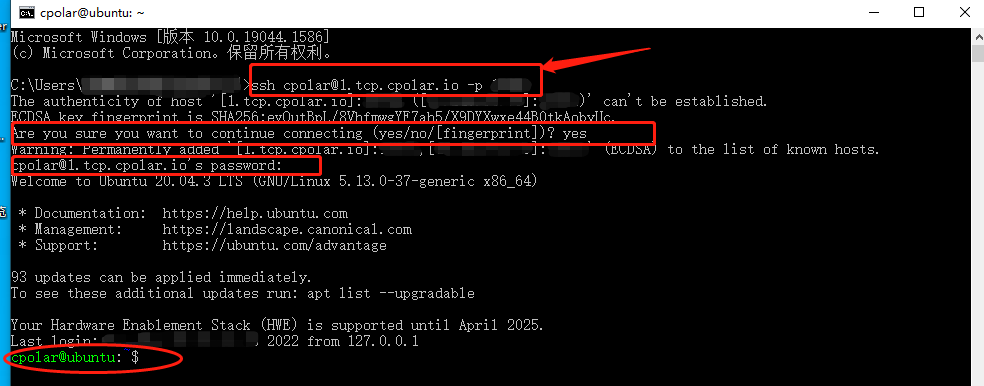
在外SSH远程连接Ubuntu系统
在外SSH远程连接Ubuntu系统【无公网IP】 文章目录 在外SSH远程连接Ubuntu系统【无公网IP】前言1. 在Ubuntu系统下安装cpolar软件2. 完成安装后打开cpolar客户端web—UI界面3. 创建隧道取得连接Ubuntu系统公网地址4. 打开Windows的命令界面并输入命令 前言 随着科技和经济的发展…...
GOTS标准速递---7.0 版将于2024年3月1日起全面生效
【GOTS标准速递---7.0 版将于2024年3月1日起全面生效】 全球有机纺织品标准很高兴地宣布发布GOTS 7.0 版，该版本扩大了环境和社会标准的范围，同时保持了适用于工业生产并适用于各种产品的标准。在为期一年的定期修订过程中，在有机生产、纺织品…...
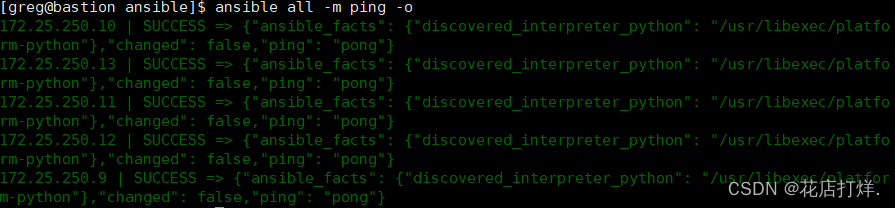
Ansible的安装和配置
安装和配置 Ansible 安装所需的软件包 创建名为 /home/greg/ansible/inventory 的静态清单文件，以满足以下要求： 172.25.250.9 是 dev 主机组的成员 172.25.250.10 是 test 主机组的成员 172.25.250.11 和 172.25.250.12 是 prod 主机组的成员 172.2…...
口-肠-脑轴与精神健康的关系
谷禾健康 在个体中，每个微生物栖息地都表现出独特的微生物种群模式。迄今为止，关于微生物组相关疾病的研究主要集中在器官特异性微生物组上。然而，器官间的微生物网络正逐渐成为生理功能和病理过程中的重要调节因子和治疗机会。 在正常情况下…...
Dubbo是干嘛的，Dubbo原理和机制，Dubbo的核心组件
目录 一、介绍1、Dubbo是什么2、为什么需要Dubbo3、Dubbo的特性 二、 Dubbo的核心概念1、暴露和引用（Export and Refer）2、服务提供者和服务消费者3、注册中心4、负载均衡5、集群容错 三、Dubbo的架构1、服务提供者和服务消费者之间的通信流程2、Dubbo的…...
自动zksync刷账户交互（附代码）
自动化任务的 Python 代码。它使用 Selenium 库来控制浏览器。 #解锁小狐狸 task.unlock_metamask(ads) #zk主网连接钱包，初始化 #ZK主网任务1：转账 print(选择ZK主网任务1：转账) task.zk_task1(ads,address) #…...
荐读 | 《揭秘云计算与大数据》
当我们回顾过去几十年的科技进步时，云计算和大数据在现代科技发展史上无疑具有里程碑式的意义，它们不仅改变了我们的生活方式，而且对各行各业产生了深远的影响。 在这个数字化时代，云计算和大数据技术已经成为推动全球发展的关键…...
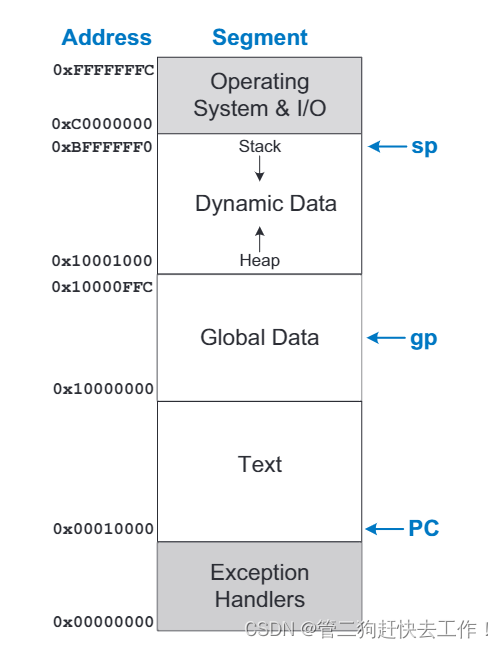
RISC-V基础之内存分布与映射
内存映射是指将地址空间划分为不同的部分或段，每个段有不同的用途和属性。这段话介绍了五个段：文本段、全局数据段、动态数据段、异常处理器段和操作系统（OS）段。下面是对每个段的简要说明： 文本段：存放程序…...
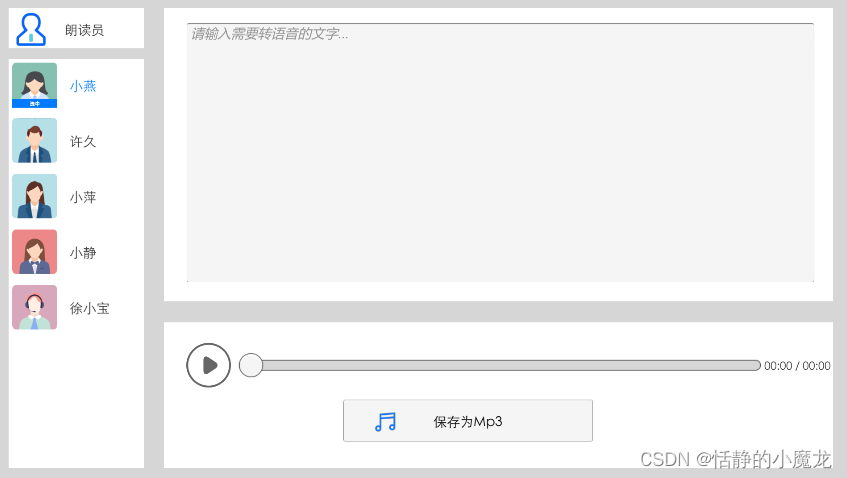
【Unity3D应用案例系列】Unity3D中实现文字转语音的工具开发
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址我的个人博客 大家好，我是佛系工程师☆恬静的小魔龙☆，不定时更新Unity开发技巧，觉得有用记得一键三连哦。 一、前言 在开发中，会遇到将文字转语音输出的需求࿰…...
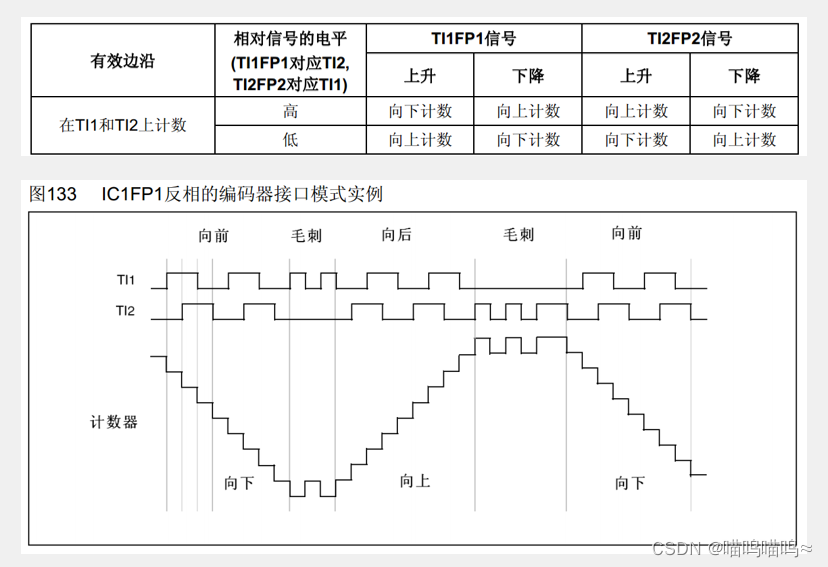
STM32入门——定时器
内容为江科大STM32标准库学习记录 TIM简介 TIM（Timer）定时器定时器可以对输入的时钟进行计数，并在计数值达到设定值时触发中断16位计数器、预分频器、自动重装寄存器的时基单元，在72MHz计数时钟下可以实现最大59.65s的定时&…...
企业工商信息：知识产权出质
一、出质是什么？质权是什么？ 出质，作为一种物权行为，是指将个人或企业所拥有的财产权益移交给他人作为抵押，以获得资金支持。这一概念在商业活动中扮演着重要的角色，为企业创造了融资渠道。特别是在知识密…...
batch_softmax_loss
每个用户抽取一定数量的困难负样本，然后ssm def batch_softmax_loss_neg(self, user_idx, rec_user_emb, pos_idx, item_emb):user_emb rec_user_emb[user_idx]product_scores torch.matmul(F.normalize(user_emb, dim1), F.normalize(item_emb, dim1).transpose(…...
刘汉清：从生活到画布，宠物成为灵感源泉
出生于中国镇江的艺术家刘汉清，其作品展现出他对日常生活的深入洞察力，以及对美的独特理解。他的作品通常没有视觉参考，而是通过对他周围环境的理解，尤其是他的宠物，来进行创作。 在刘汉清的创作过程中，他…...
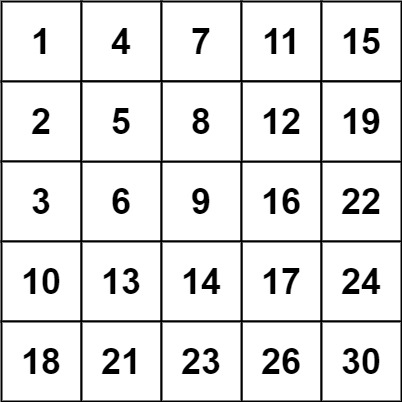
【LeetCode】240.搜索二维矩阵Ⅱ
题目 编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性： 每行的元素从左到右升序排列。每列的元素从上到下升序排列。 示例 1： 输入：matrix [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,…...
SED正则表达式中[方括号]的特殊处理
今天被这个方括号懵晕了，特此记录 例如： 去除输入字符串“1[2.3]4[ab,c]”中的所有方括号和逗号： $ echo "1[2.3]4[ab,c]"|sed -e "s/[,\]\[]//g" 1[2.3]4[ab,c] It doesnt work! 原因：Regular Expressi…...
Android 音频开发
在Android平台上进行音频开发，您需要掌握以下关键知识点： Android平台基础知识：熟悉Android操作系统的基本架构、组件和应用开发的基本概念。 音频API：了解Android提供的音频相关API，主要包括android.media.AudioReco…...
Java8新特性,Lambda,Stream流
Java8新特性,Lambda,Stream流 Java8版本在2014年3月18日发布，为Java语言添加了很多重要的新特性。新特性包括：Lambda表达式、方法引用、默认方法、新的时间日期API、Stream API、Optional类等等。这些新特性大大增强了Java语言的表达能力，使…...
模型训练之train.py代码解析
题目 作者：安静到无声 个人主页 from __future__ import absolute_import from __future__ import division from __future__ import print_function这段代码使用了Python 2.x的__future__模块来导入Python 3.x的一些特性。在Python 2.x中，使用print语句来输出内容，而在Py…...
: K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？)
云原生核心技术 (7/12): K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？
大家好，欢迎来到《云原生核心技术》系列的第七篇！ 在上一篇，我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在，我们就像一个拥有了一块崭新数字土地的农场主，是时…...
TDengine 快速体验（Docker 镜像方式）
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能，本节首先介绍如何通过 Docker 快速体验 TDengine，然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker，请使用 安装包的方式快…...
vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径：src/utils/timer.ts 完整代码： import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
Python如何给视频添加音频和字幕
在Python中，给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加，包括必要的代码示例和详细解释。 环境准备 在开始之前，需要安装以下Python库：…...
【VLNs篇】07：NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战，克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
GO协程(Goroutine)问题总结
在使用Go语言来编写代码时，遇到的一些问题总结一下 [参考文档]：https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现： 今天在看到这个教程的时候，在自己的电…...
Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API，让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API，你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
macOS 终端智能代理检测
🧠 终端智能代理检测：自动判断是否需要设置代理访问 GitHub 在开发中，使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新，例如： fatal: unable to access https://github.com/ohmyzsh/oh…...
一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序，无论是测试应用程序、搜寻漏洞还是收集情报，它们都能提升工作流程。 FoxyProxy 代理管理工具，此扩展简化了使用代理（如 Burp…...