题解 | #1002.Random Nim Game# 2023杭电暑期多校7
1002.Random Nim Game
诈骗博弈题
题目大意
Nim是一种双人数学策略游戏,玩家轮流从不同的堆中移除棋子。在每一轮游戏中,玩家必须至少取出一个棋子,并且可以取出任意数量的棋子,条件是这些棋子都来自同一个棋子堆。走最后一步棋(即取出最后一块棋子)的人获胜。
现在更改游戏规则,在每个回合中,棋手必须选择一个棋子堆。假设他选择的堆包含 x x x 个棋子,将从 [ 1 , x ] [1,x] [1,x] 中随机一个整数 y y y ,并从堆中移除 y y y 个棋子
求先手获胜的概率,答案取模
解题思路
看起来很吓人的一道题(谁被吓退了我不说)//
考虑只有一个堆的情况
若只有 1 1 1 个棋子,先手必胜
如果有 2 2 2 个棋子,有 1 2 \dfrac{1}{2} 21 的概率拿完获胜,有 1 2 \dfrac{1}{2} 21 的概率余 1 1 1 失败,综合胜率 1 2 \dfrac{1}{2} 21
⋮ \vdots ⋮
如果有 x ( x > 1 ) x\ (x>1) x (x>1) 个棋子,有 n − 2 n \dfrac{n-2}{n} nn−2 的概率转移到 剩余个数 > 1 >1 >1 的状态,有 1 n \dfrac{1}{n} n1 的概率拿完获胜,有 1 n \dfrac{1}{n} n1 的概率余 1 1 1 失败。递归得到 x > 1 x>1 x>1 的状态下的综合胜率为 1 2 \dfrac{1}{2} 21
再考虑多堆的情况
如果所有堆的棋子数量均为 1 1 1 ,则当堆数 n n n 为奇数时先手必胜
如果有某堆的数量多于 1 1 1 个,那么必胜态将以 1 2 \dfrac{1}{2} 21 的概率流转
综上所述,如果所有堆的棋子数量均为 1 1 1 ,则当堆数 n n n 为奇数时先手必胜, n n n 为偶数时先手必败,其余情况综合胜率 1 2 \dfrac{1}{2} 21
参考代码
参考代码为已AC代码主干,其中部分功能需读者自行实现
void solve()
{ll n;cin >> n;ll mx=0,t;FORLL(i,1,n){cin >> t;mx=max(mx,t);}if(mx>1) cout << inv(2) << endl;else if(n%2) cout << 1 << endl;else cout << 0 << endl;
}
相关文章:

题解 | #1002.Random Nim Game# 2023杭电暑期多校7
1002.Random Nim Game 诈骗博弈题 题目大意 Nim是一种双人数学策略游戏,玩家轮流从不同的堆中移除棋子。在每一轮游戏中,玩家必须至少取出一个棋子,并且可以取出任意数量的棋子,条件是这些棋子都来自同一个棋子堆。走最后一步棋…...

篇九:组合模式:树形结构的力量
篇九:“组合模式:树形结构的力量” 开始本篇文章之前先推荐一个好用的学习工具,AIRIght,借助于AI助手工具,学习事半功倍。欢迎访问:http://airight.fun/。 另外有2本不错的关于设计模式的资料,…...
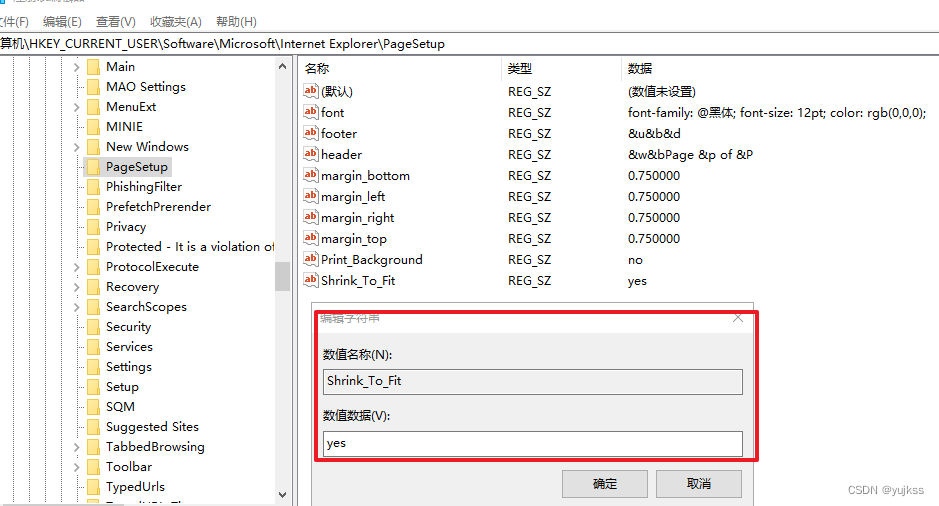
【注册表】windows系统注册表常用修改方案
文章目录 ◆ 修改IE浏览器打印页面参数设置◆气泡屏幕保护◆彩带屏幕保护程序◆过滤IP(适用于WIN2000)◆禁止显示IE的地址栏◆禁止更改IE默认的检查(winnt适用)◆允许DHCP(winnt适用)◆局域网自动断开的时间(winnt适用)◆禁止使用“重置WEB设置”◆禁止更…...

ant-design-vue 4.x升级问题-样式丢失问题
[vue] ant-design-vue 4.x升级问题-样式丢失问题 项目环境问题场景解决方案 该文档是在升级ant-design-vue到4.x版本的时候遇到的问题 项目环境 "vue": "^3.3.4", "ant-design-vue": "^4.0.0", "vite": "^4.4.4&quo…...

【果树农药喷洒机器人】Part3:变量喷药系统工作原理介绍
本专栏介绍:免费专栏,持续更新机器人实战项目,欢迎各位订阅关注。 关注我,带你了解更多关于机器人、嵌入式、人工智能等方面的优质文章! 文章目录 一、变量喷药系统工作原理二、液压通路设计与控制系统封装2.1液压通路…...

GoogLeNet创新点总结
GoogLeNet是一种深度卷积神经网络架构,于2014年由Google团队提出,是ILSVRC(ImageNet Large Scale Visual Recognition Challenge)比赛的冠军模型,其创新点主要集中在以下几个方面: Inception模块&#…...
)
不同路径1、2、3合集(980. 不同路径 III)
不同路径一 矩形格,左上角 到 右下角。 class Solution {int [] directX new int[]{-1,1,0,0};int [] directY new int[]{0,0,-1,1};int rows;int cols;public int uniquePathsIII(int[][] grid) {if (grid null || grid.length 0 || grid[0].length 0) {ret…...

【云原生】Yaml文件详解
目录 一、YAML 语法格式1.1查看 api 资源版本标签1.2 写一个yaml文件demo1.3 详解k8s中的port 一、YAML 语法格式 Kubernetes 支持 YAML 和 JSON 格式管理资源对象JSON 格式:主要用于 api 接口之间消息的传递YAML格式:用于配置和管理,YAML 是…...

ffmpeg下载安装教程
ffmpeg官网下载地址https://ffmpeg.org/download.html 这里以windows为例,鼠标悬浮到windows图标上,再点击 Windows builds from gyan.dev 或者直接打开 https://www.gyan.dev/ffmpeg/builds/ 下载根据个人需要下载对应版本 解压下载的文件,并复制bin所在目录 新打开一个命令…...
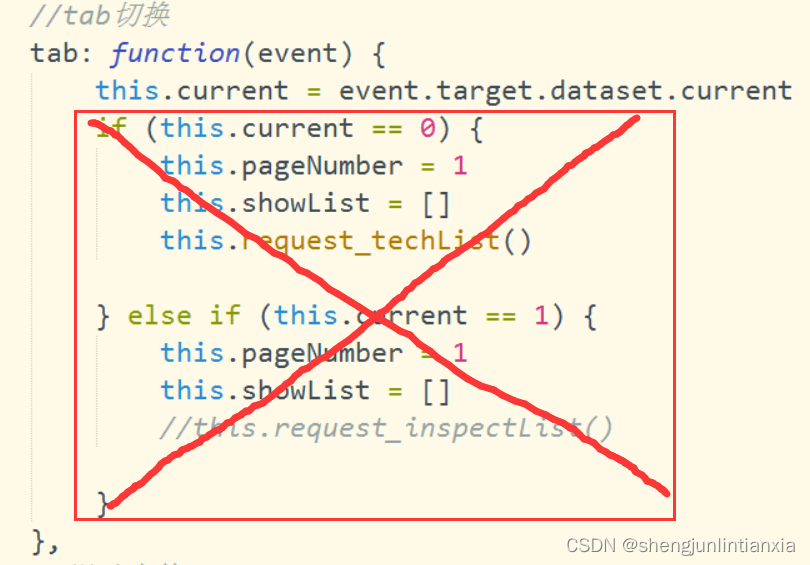
uniapp之当你问起“tab方法触发时eventchange也跟着触发了咋办”时
我相信没有大佬会在这个问题上卡两个小时吧,记下来大家就当看个乐子了。 当时问题就是,点击tab头切换的时候,作为tab滑动事件的eventchange同时触发了,使得接口请求了两次 大概是没睡好,我当时脑子老想着怎么阻止它冒…...
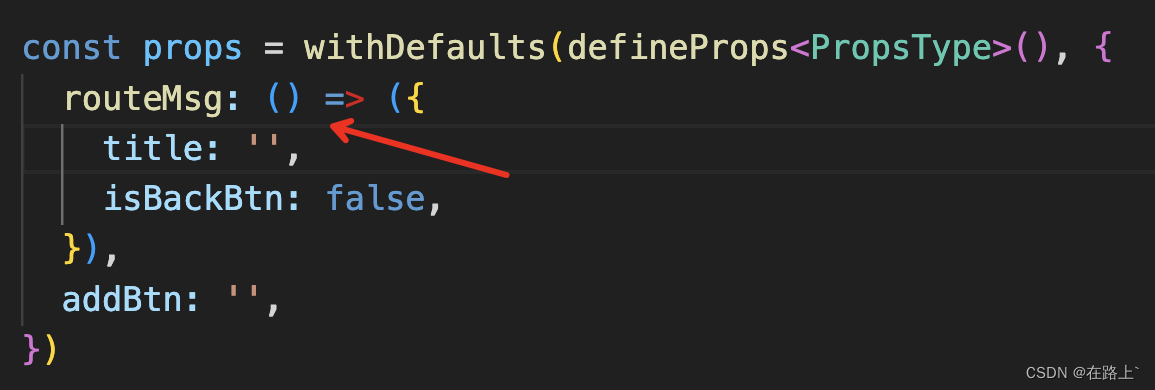
TS 踩坑之路(四)之 Vue3
一、在使用定义默认值withDefaults和defineProps 组合时,默认值设置报错 代码案例 报错信息 不能将类型“{ isBackBtn: false; }”分配给类型“(props: PropsType) > RouteMsgType”。 对象字面量只能指定已知属性,并且“isBackBtn”不在类型“(pro…...
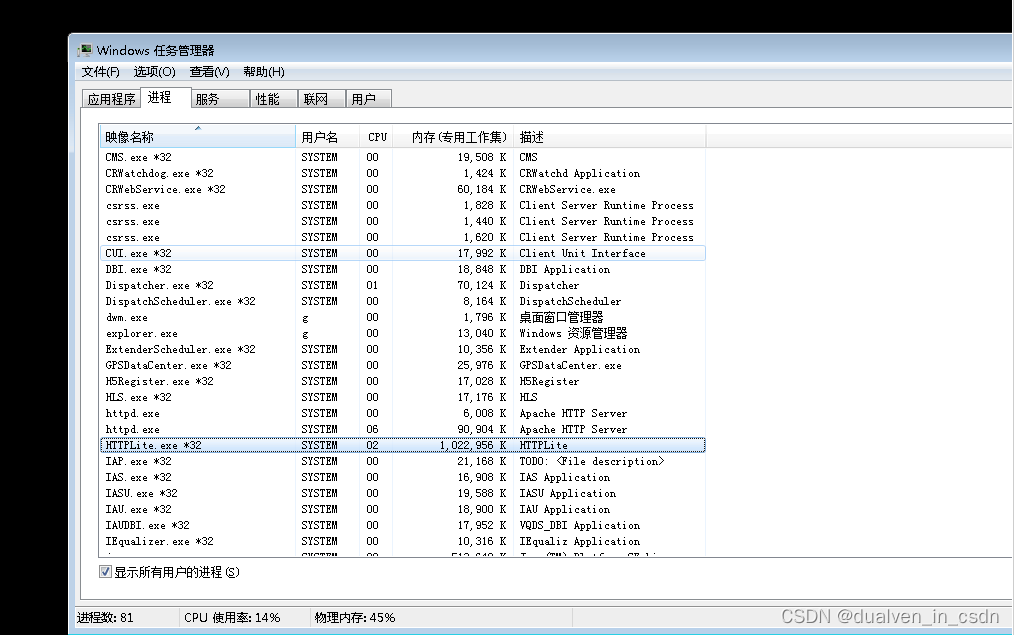
【音视频】edge与chrome在性能上的比较
目录 结论先说 实验 结论 实验机器的cpu配置 用EDGE拉九路编辑 google拉五路就拉不出来了 资源使用情况 edge报错编辑 如果服务器端 性能也满 了,就会不回复;验证方式 手动敲 8081,不回应。 结论先说 实验 用chrome先拉九路&#…...
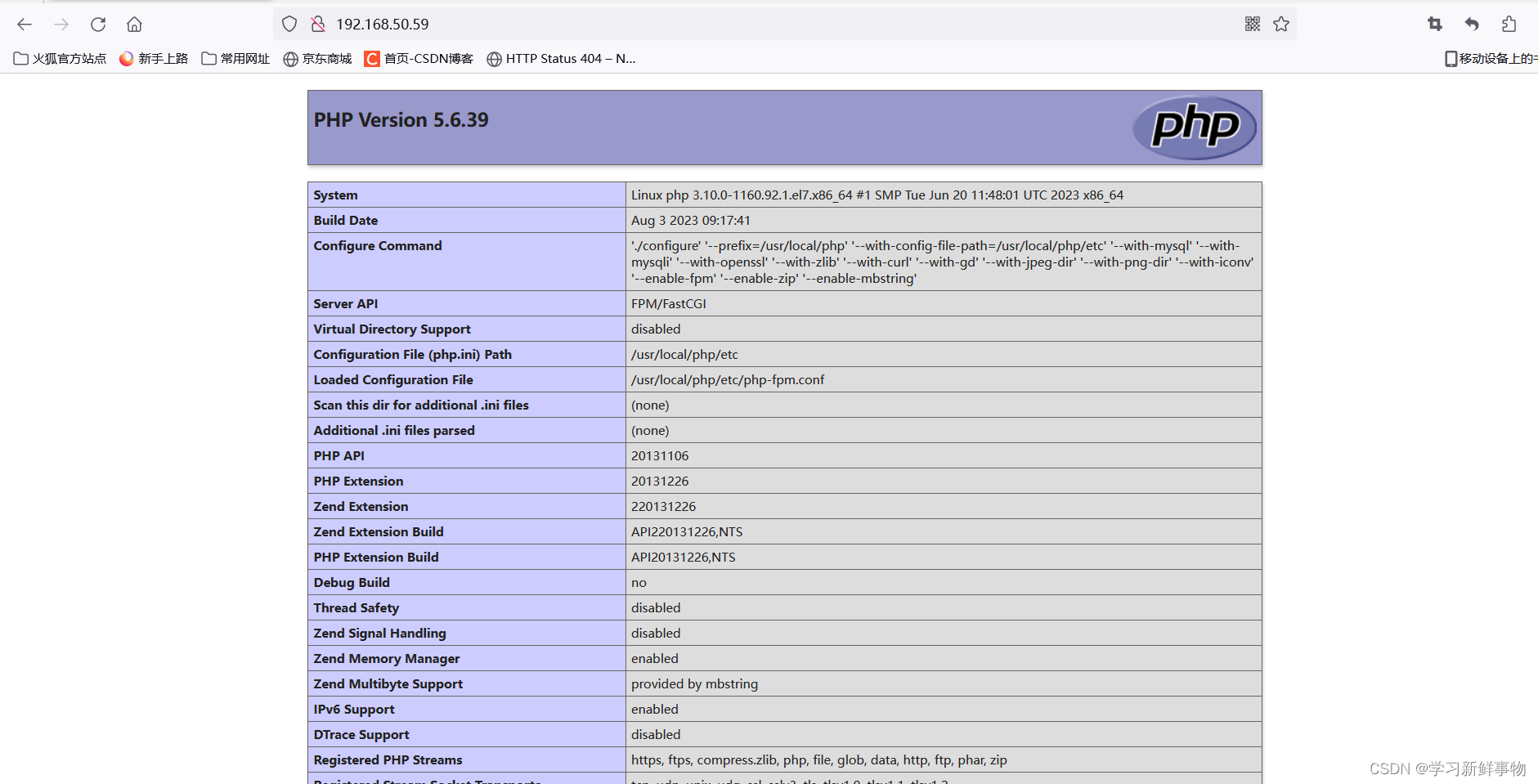
Docker Compose编排部署LNMP服务
目录 安装docker-ce 阿里云镜像加速器 文件 启动 安装docker-ce [rootlocalhost ~]# wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repo --2023-08-03 18:34:32-- http://mirrors.aliyun.com/repo/Centos-7.repo 正在解析主机 m…...
git使用(常见用法)
一.下载git git官方下载跳转 安装简单,有手就行 二. git的简单使用 1. 连接远程仓库 #初始化 git init #配置账户 git config --global user.name “输入你的用户名” git config --global user.email “输入你的邮箱” git config --list #--q退出 #配置验证邮箱 ssh-key…...

用例拆分情况考虑方案
文章目录 1、方案一方案概述方案分析(1) 把对应图商地图的逻辑给分离开(2) 要使用命令行的方式执行方法 2、方案二3、最终决定 1、方案一 方案概述 每个图商(GD、BD、自建)拆分成单独的类 把参数化的几个图商类别拆分成对应的图商类,在每个类…...

一文搞懂IS-IS报文通用格式
报文格式 IS-IS报文是直接封装在数据链路层的帧结构中的。PDU可以分为两个部分,报文头和变长字段部分。其中头部又可分为通用头部和专用头部。对于所有PDU来说,通用报头都是相同的,但专用报头根据PDU类型不同而有所差别。 IS-IS的PDU有4种类…...

位置参数 关键字参数
在Python中,函数参数可以按照位置或关键字来传递。这导致了两种主要的参数类型:位置参数和关键字参数。 位置参数: 这是最常见的参数类型,当我们调用函数时,传递给函数的参数值是按照它们的位置来确定的。例如,def fun…...

【果树农药喷洒机器人】Part5:基于深度相机与分割掩膜的果树冠层体积探测方法
文章目录 一、引言二、树冠体积测量对比方法2.1冠层体积人工测量法2.2冠层体积拟合测量法 三、基于深度相机与分割掩膜探测树冠体积方法3.1像素值与深度值的转换3.2树冠体积视觉探测法3.3实验分析 总结 一、引言 果树靶标探测是实现农药精准喷施的关键环节,本章以果…...
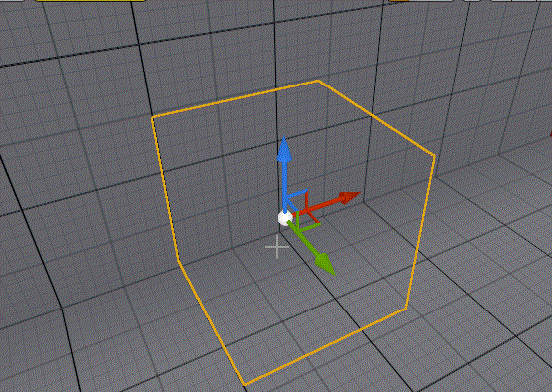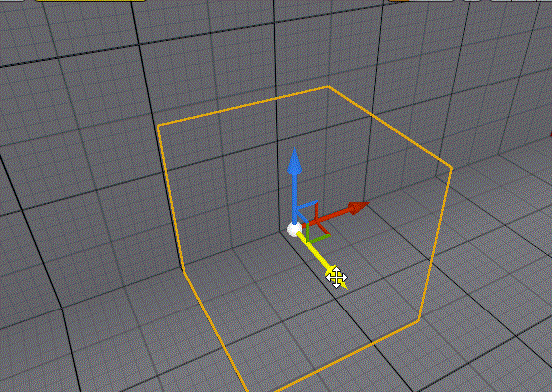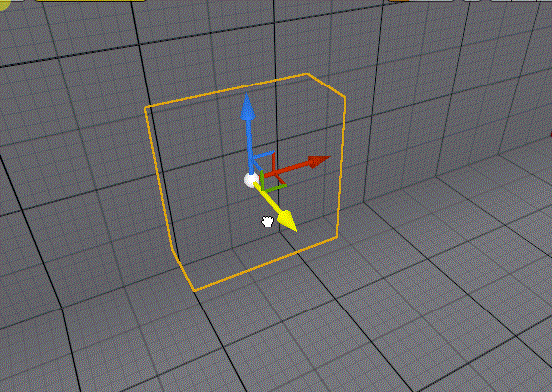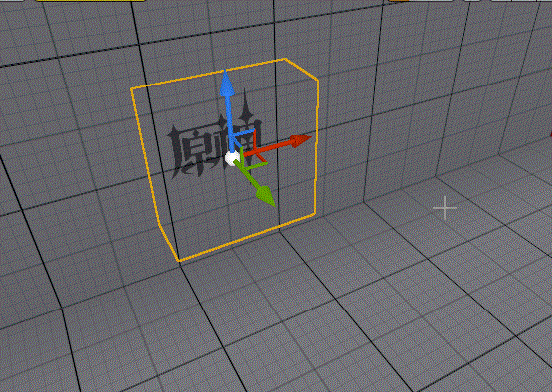
生活小妙招之UE custom Decal
因为这几年大部分时间都在搞美术,所以博客相关的可能会鸽的比较多,阿巴阿巴 https://twitter.com/Tuatara_Games/status/1674034744084905986 之前正好看到一个贴花相关的小技巧,正好做一个记录,也在这个的基础上做一些小的拓展…...

DAY02_Spring—第三方资源配置管理Spring容器Spring注解开发Spring整合Mybatis和Junit
目录 一 第三方资源配置管理1 管理DataSource连接池对象问题导入1.1 管理Druid连接池1.2 管理c3p0连接池 2 加载properties属性文件问题导入2.1 基本用法2.2 配置不加载系统属性2.3 加载properties文件写法 二 Spring容器1 Spring核心容器介绍问题导入1.1 创建容器1.2 获取bean…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
