C++ 多态深入解析
文章目录
- 前言
- 一、什么是多态
- 二、如何实现多态
- 三、代码讲解
- 四、静态联编,动态联编
- 总结
前言
在C++编程中,多态性(Polymorphism)是一种重要的概念,它允许基于对象的实际类型来调用不同的函数。多态性提供了灵活性和可扩展性,使得代码更易于维护和扩展。
一、什么是多态
多态性的定义:
多态性是一种面向对象编程的特性,它允许使用基类的指针或引用来调用派生类对象的特定成员函数。多态性能够在编译时或运行时确定函数的调用,从而实现不同的行为。
例如:
定义一个基类的 指针 p , 基类 和 子类的都定义有 print() 函数。当 p 指向一个父类的对象时,会调用父类的 print 函数;当 p 指向一个 子类对象时, 会调用 子类的 print 函数。(如下图)
注意:
这里 的 两个 print 函数并不是 函数重载,因为 函数重载要发生在同一个作用域内。这 属于函数重写。

二、如何实现多态
C++ 语言 直接支持多态的概念。
- 通过使用
virtual关键字 对多态进行支持。 - 被 virtual 声明的函数被重写后具有多态特性。
- 被 virtual 声明的函数叫做
虚函数。
class Base {
public:virtual void display() // virtual 虚函数{cout << "Base class display function" << endl;}
};
如果一个基类中有虚函数,说明 它可能被继承。子类中可能重新定义了 该函数的新用法。
三、代码讲解
下面代码中 ,父类 和 子类中 都定义了 print 函数。当 父类指针 指向不同的对象时,会根据实际的对象类型决定函数的具体目标。
class Parent // 父类 (基类)
{
public:virtual void print() // 虚函数{ printf("I'm parent.\n");}
};class Child : public Parent // 继承 Parent 的子类
{
public:void print() //重定义 该函数的新用法{printf("I'm Child\n");}
};void to_printf(Parent* p) // 参数为 父类指针,用于指向 父类/子类对象
{p->print();
}int main(void)
{Parent p1;Child c1;to_printf(&p1); //指向 父类对象,调用父类的 print 函数to_printf(&c1); //指向 子类对象,调用子类的 print 函数return 0;
}
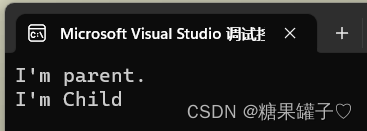
当调用 print 函数时, 同样的调用语句 在实际运行时有多种不同的表现形态,体现了多态性。
注意:
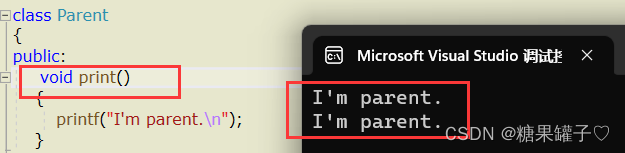
如果,没有 加上 关键字 virtual ,则两次都会调用 父类的函数。因为 编译器不知道指针 p 究竟指向了什么,为了更安全,编译器就直接调用了父类的函数,赋值兼容性。
四、静态联编,动态联编
理论的概念:
静态联编: 在程序的编译期间就能确定具体的函数调用。
如: 函数重载。
动态联编: 在程序运行后才能确定具体的函数调用。
如:函数重写。
总结
多态性 是 C++ 编程中一个重要且强大的概念。通过使用虚函数和函数重写,我们可以实现多态性,从而提高代码的可维护性、可扩展性和灵活性。在编写代码时,我们应该充分利用多态性的优势,并遵循良好的面向对象设计原则来正确使用多态性。
相关文章:

C++ 多态深入解析
文章目录 前言一、什么是多态二、如何实现多态三、代码讲解四、静态联编,动态联编总结 前言 在C编程中,多态性(Polymorphism)是一种重要的概念,它允许基于对象的实际类型来调用不同的函数。多态性提供了灵活性和可扩展…...
C#使用EmguCV播放视频
目录 一、前言 1、简介 2、测试工程代码下载链接 3、EmguCV 库文件下载链接 二、工程环境配置 1、EmguCV控件添加引用 (1)窗口控件添加 (2)相关Dll文件添加添加引用 (3)工程运行基础文件夹添加 &a…...
LeetCode150道面试经典题-买卖股票的最佳时机(简单)
1、题目 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交易中获取的…...
【积水成渊】CSS磨砂玻璃效果和渐变主题色文字
大家好,我是csdn的博主:lqj_本人 lqj_本人_python人工智能视觉(opencv)从入门到实战,前端,微信小程序-CSDN博客 最新的uniapp毕业设计专栏也放在下方了: https://blog.csdn.net/lbcyllqj/category_12346639.html?spm1…...
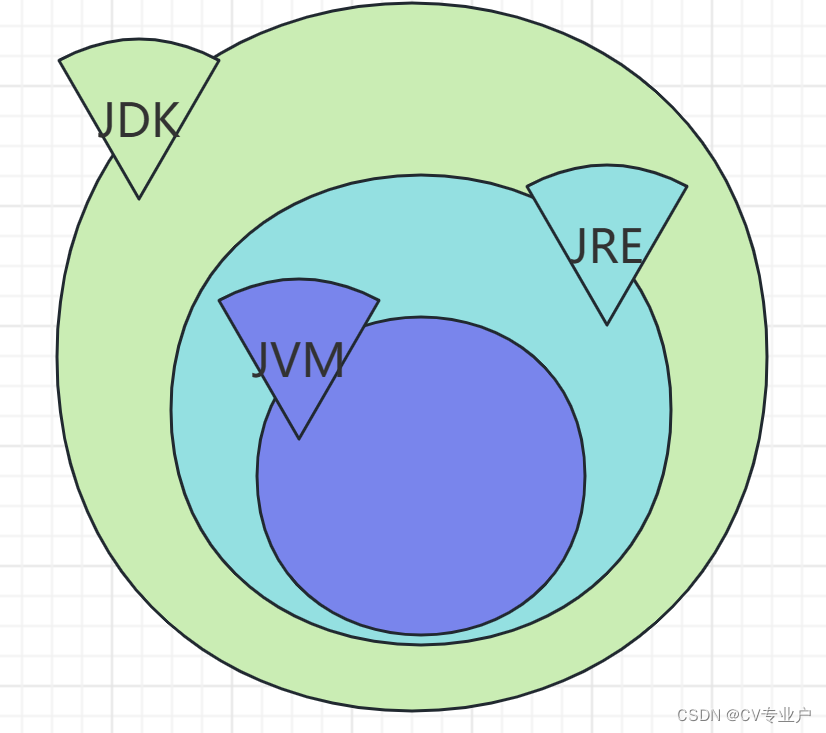
JVM、JRE、JDK三者之间的关系
JVM、JRE和JDK是与Java开发和运行相关的三个重要概念。 再了解三者之前让我们先来了解下java源文件的执行顺序: 使用编辑器或IDE(集成开发环境)编写Java源文件.即demo.java程序必须编译为字节码文件,javac(Java编译器)编译源文件为demo.class文件.类文…...

input 标签的 type 属性有哪些值?分别表示什么意思?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ type值以及作用⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端…...
(十五)大数据实战——hive的安装部署
前言 Hive是由Facebook开源,基于Hadoop的一个数据仓库工具,可以将结构化的数据文件映射为一张表,并提供类SQL查询功能。本节内容我们主要介绍一下hive的安装与部署的相关内容。 正文 上传hive安装包到hadoop101服务器/opt/software目录 解…...
MySQL安装和卸载
1.MySQL概述 MySQL概述 MySQL是一个[关系型数据库管理系统],由瑞典MySQL AB 公司开发,2008年被sun公司收购, 2009sun又被oracle收购,所以属于 Oracle 旗下产品。MySQL 是最流行的关系型数据库管理系统之一,在 WEB 应用…...
ELK、ELFK日志分析系统
菜单一、ELK简介1.1 ELK组件说明1.1.1 ElasticSearch1.1.2 Kiabana1.1.3 Logstash 1.2 可以添加的其它组件1.2.1 Filebeat1.2.2 缓存/消息队列(redis、kafka、RabbitMQ等)1.2.3 Fluentd 1.3 为什么要用ELK1.4 完整日志系统的基本特征1.5 ELK 的工作原理 …...

JVM基础篇-StringTable
StringTable 特性 常量池中的字符串仅是符号,第一次用到时才变为对象 利用串池的机制,来避免重复创建字符串对象 字符串变量拼接的原理是 StringBuilder (1.8) 字符串常量拼接的原理是编译期优化 可以使用 intern 方法&#…...
探秘手机隐藏的望远镜功能:开启后,观察任何你想看的地方
当今的智能手机不仅仅是通信工具,它们蕴藏着各种隐藏的功能,其中之一就是让你拥有望远镜般的观察能力。是的,你没有听错!今天我们将探秘手机中隐藏的望远镜功能,这项神奇的功能可以让你打开后,轻松观察任何…...

正运动亮相2023半导体设备材料与核心部件展示会,助力半导体产业高速高精应用
■展会名称: 第11届(2023)半导体设备材料与核心部件展示会 ■展会日期 2023年8月9日-11日 ■展馆地点 无锡太湖国际博览中心A6馆 ■展位号 A6-A361 正运动技术,作为国内领先的运动控制企业,将于2023年8月9日参加…...

如何在MongoDB中添加新用户
如何在MongoDB中添加新用户? MongoDB是一款流行的NoSQL数据库,它的可扩展性强,可进行分布式部署,且具有高可用性。其许多优势使得越来越多的企业和组织选择MongoDB作为其数据库系统。本文将介绍如何在MongoDB中添加新用户。 第一步…...
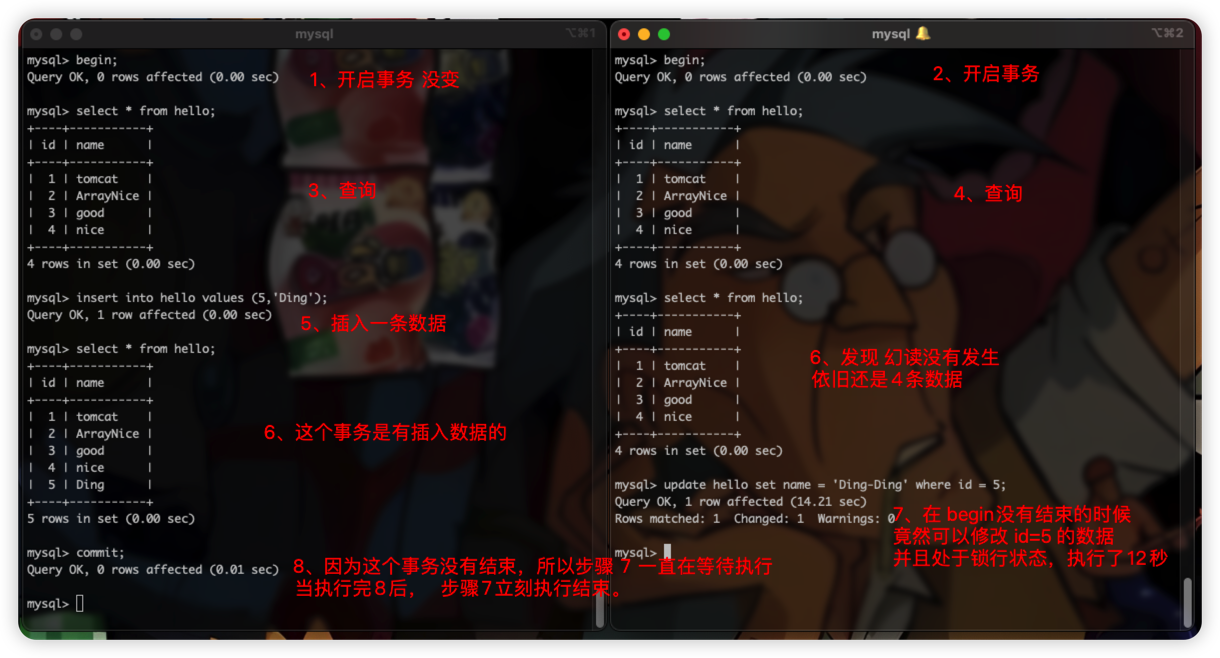
幻读怎么复现
大家好,我是想想。 很久没有给大家分享技术了,主要在计划一些事情,几乎没什么时间爽文了。 今天从实操上实现了MySQL事务隔离复现问题,就记录分享给大家吧。 正文 我们知道,著名的四大事务特性ACID特性 Atomicity…...
无脑入门pytorch系列(二)—— torch.mean
本系列教程适用于没有任何pytorch的同学(简单的python语法还是要的),从代码的表层出发挖掘代码的深层含义,理解具体的意思和内涵。pytorch的很多函数看着非常简单,但是其中包含了很多内容,不了解其中的意思…...

ansible-kubeadm在线安装高可用K8S集群v1.19-v1.20版本
ansible可以安装的KS8版本如下: 请按照此博客中的内容操作后,才可以通过下面的命令查询到版本。 [rootk8s-master01 ~]# yum list kubectl --showduplicates | sort -r kubectl.x86_64 1.20.0-0 kubern…...

Cesium entity 渐隐渐显、闪烁
点entity function f2(){var x1;var flogtrue;//闪烁//var x0;var flogfalse;//渐显viewer.entities.add({name:"圆点point闪烁",position:Cesium.Cartesian3.fromDegrees(116.200.03,39.530.03,0),point : {show : true, // defaultcolor :new Cesium.CallbackProp…...

LISA:通过大语言模型进行推理分割
论文:https://arxiv.org/pdf/2308.00692 代码:GitHub - dvlab-research/LISA 摘要 尽管感知系统近年来取得了显著的进步,但在执行视觉识别任务之前,它们仍然依赖于明确的人类指令来识别目标物体或类别。这样的系统缺乏主动推理…...

opencv基础40-礼帽运算(原始图像减去其开运算)cv2.MORPH_TOPHAT
礼帽运算是用原始图像减去其开运算图像的操作。礼帽运算能够获取图像的噪声信息,或者得到比原始图像的边缘更亮的边缘信息。 例如,图 8-22 是一个礼帽运算示例,其中: 左图是原始图像。中间的图是开运算图像。右图是原始图像减开运…...
函数)
php中的array_filter()函数
php中的array_filter()函数用于筛选数组中的元素,并返回一个新的数组,新数组的元素是所有返回值为true的原数组元素。 array_filter()函数的使用语法如下: array_filter ( array $array [, callable $callback [, int $flag 0 ]] ) : array…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

MeshGPT 笔记
[2311.15475] MeshGPT: Generating Triangle Meshes with Decoder-Only Transformers https://library.scholarcy.com/try 真正意义上的AI生成三维模型MESHGPT来袭!_哔哩哔哩_bilibili GitHub - lucidrains/meshgpt-pytorch: Implementation of MeshGPT, SOTA Me…...

项目进度管理软件是什么?项目进度管理软件有哪些核心功能?
无论是建筑施工、软件开发,还是市场营销活动,项目往往涉及多个团队、大量资源和严格的时间表。如果没有一个系统化的工具来跟踪和管理这些元素,项目很容易陷入混乱,导致进度延误、成本超支,甚至失败。 项目进度管理软…...

PostgreSQL 对 IPv6 的支持情况
PostgreSQL 对 IPv6 的支持情况 PostgreSQL 全面支持 IPv6 网络协议,包括连接、存储和操作 IPv6 地址。以下是详细说明: 一、网络连接支持 1. 监听 IPv6 连接 在 postgresql.conf 中配置: listen_addresses 0.0.0.0,:: # 监听所有IPv4…...

Java严格模式withResolverStyle解析日期错误及解决方案
在Java中使用DateTimeFormatter并启用严格模式(ResolverStyle.STRICT)时,解析日期字符串"2025-06-01"报错的根本原因是:模式字符串中的年份格式yyyy被解释为YearOfEra(纪元年份),而非…...

【Linux应用】Linux系统日志上报服务,以及thttpd的配置、发送函数
【Linux应用】Linux系统日志上报服务,以及thttpd的配置、发送函数 文章目录 thttpd服务安装thttpd配置thttpd服务thttpd函数日志效果和文件附录:开发板快速上手:镜像烧录、串口shell、外设挂载、WiFi配置、SSH连接、文件交互(RADX…...
