如何在MongoDB中添加新用户
如何在MongoDB中添加新用户?
MongoDB是一款流行的NoSQL数据库,它的可扩展性强,可进行分布式部署,且具有高可用性。其许多优势使得越来越多的企业和组织选择MongoDB作为其数据库系统。本文将介绍如何在MongoDB中添加新用户。
第一步:连接MongoDB数据库
先安全登录方式启动MongoDB服务
mongod -f ../conf/mongod.conf --auth
在添加用户之前,我们需要连接到MongoDB数据库。我们可以使用MongoDB Shell、MongoDB Compass或其他MongoDB客户端工具连接到数据库。下面是使用MongoDB Shell连接到数据库的方法。
在终端或命令提示符窗口中运行mongo命令,它将启动MongoDB Shell:
mongo
然后,输入MongoDB数据库的地址和端口号(默认的MongoDB端口号为27017),例如:
mongo
如果您的MongoDB服务器需要用户名和密码进行身份验证,请输入您的用户名和密码:
mongo -uusername -ppassword --authenticationDatabase=admin
接下来,选择要使用的数据库:
use mydatabase
第二步:创建用户
创建用户的命令是db.createUser()。下面是创建一个名为John的用户的示例代码:
db.createUser({user: "admin",pwd: "admin",roles: [ "readWrite","dbAdmin","dbOwner"]
})
这将创建一个具有readWrite和dbAdmin和dbOwner角色的用户,并将其密码设置为admin。您可以将其更改为您想要的任何值。建议将密码设置为强密码,以确保安全性。
注意,在MongoDB中,用户是在特定的数据库中创建的。这意味着,如果您需要为多个数据库创建用户,则需要在每个数据库中执行db.createUser()命令。
第三步:验证用户
成功创建用户后,您可以验证此用户是否可以访问数据库。对于MongoDB Shell,请使用以下命令:
mongo -uadmin-padmin --authenticationDatabase=mydatabase
这将连接到mydatabase数据库,并进行身份验证。如果验证成功,则您将能够使用该用户执行任何操作。如果验证失败,则您需要重新检查用户的用户名和密码是否正确。
在MongoDB Compass或其他MongoDB客户端工具中,您可以使用用户的凭证连接到数据库。请查看您的客户端工具的文档以获取详细说明。
总结
在MongoDB中添加新用户非常简单。您只需要连接到数据库、创建用户并验证其凭证是否有效即可。请确保使用强密码和为每个需要访问的数据库创建不同的用户以确保安全性。
相关文章:

如何在MongoDB中添加新用户
如何在MongoDB中添加新用户? MongoDB是一款流行的NoSQL数据库,它的可扩展性强,可进行分布式部署,且具有高可用性。其许多优势使得越来越多的企业和组织选择MongoDB作为其数据库系统。本文将介绍如何在MongoDB中添加新用户。 第一步…...
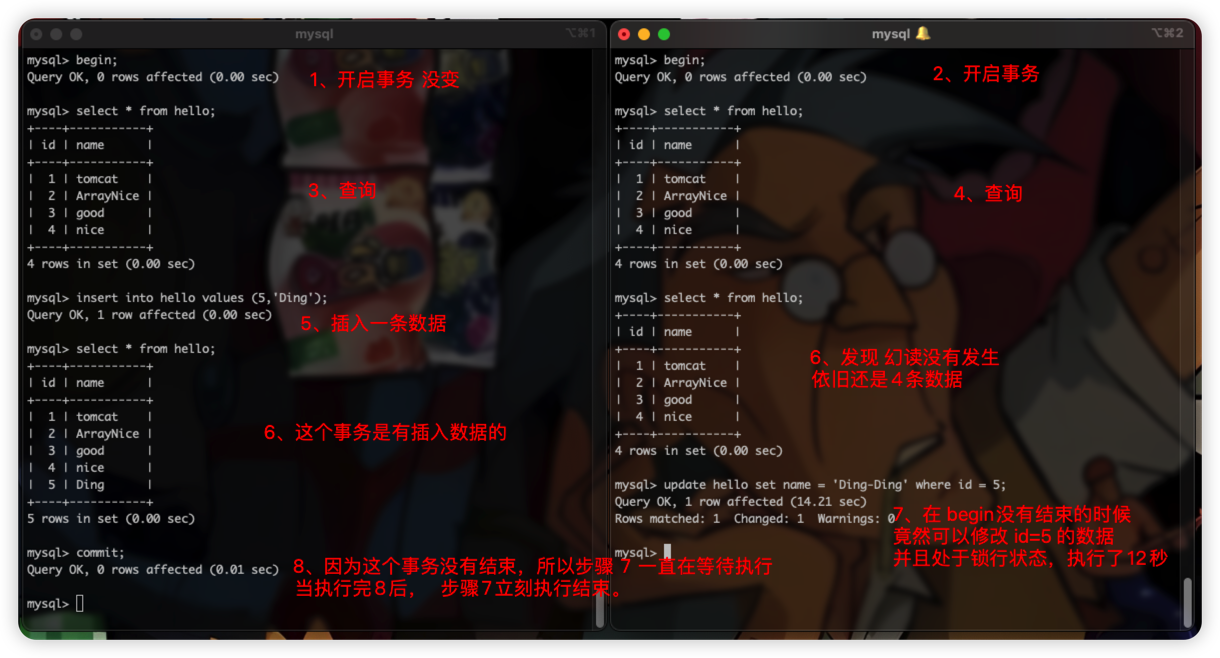
幻读怎么复现
大家好,我是想想。 很久没有给大家分享技术了,主要在计划一些事情,几乎没什么时间爽文了。 今天从实操上实现了MySQL事务隔离复现问题,就记录分享给大家吧。 正文 我们知道,著名的四大事务特性ACID特性 Atomicity…...
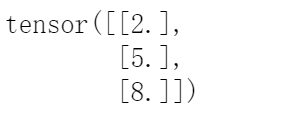
无脑入门pytorch系列(二)—— torch.mean
本系列教程适用于没有任何pytorch的同学(简单的python语法还是要的),从代码的表层出发挖掘代码的深层含义,理解具体的意思和内涵。pytorch的很多函数看着非常简单,但是其中包含了很多内容,不了解其中的意思…...

ansible-kubeadm在线安装高可用K8S集群v1.19-v1.20版本
ansible可以安装的KS8版本如下: 请按照此博客中的内容操作后,才可以通过下面的命令查询到版本。 [rootk8s-master01 ~]# yum list kubectl --showduplicates | sort -r kubectl.x86_64 1.20.0-0 kubern…...

Cesium entity 渐隐渐显、闪烁
点entity function f2(){var x1;var flogtrue;//闪烁//var x0;var flogfalse;//渐显viewer.entities.add({name:"圆点point闪烁",position:Cesium.Cartesian3.fromDegrees(116.200.03,39.530.03,0),point : {show : true, // defaultcolor :new Cesium.CallbackProp…...

LISA:通过大语言模型进行推理分割
论文:https://arxiv.org/pdf/2308.00692 代码:GitHub - dvlab-research/LISA 摘要 尽管感知系统近年来取得了显著的进步,但在执行视觉识别任务之前,它们仍然依赖于明确的人类指令来识别目标物体或类别。这样的系统缺乏主动推理…...

opencv基础40-礼帽运算(原始图像减去其开运算)cv2.MORPH_TOPHAT
礼帽运算是用原始图像减去其开运算图像的操作。礼帽运算能够获取图像的噪声信息,或者得到比原始图像的边缘更亮的边缘信息。 例如,图 8-22 是一个礼帽运算示例,其中: 左图是原始图像。中间的图是开运算图像。右图是原始图像减开运…...
函数)
php中的array_filter()函数
php中的array_filter()函数用于筛选数组中的元素,并返回一个新的数组,新数组的元素是所有返回值为true的原数组元素。 array_filter()函数的使用语法如下: array_filter ( array $array [, callable $callback [, int $flag 0 ]] ) : array…...
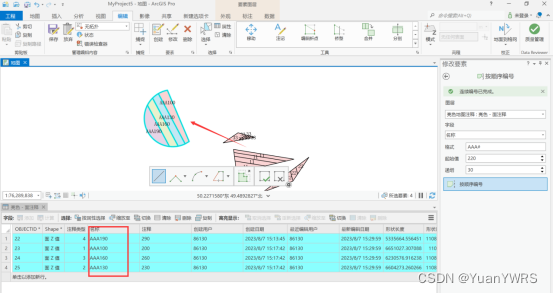
ArcGIS Pro基础:【按顺序编号】工具实现属性字段的编号自动赋值
本次介绍一个字段的自动排序编号赋值工具,基于arcgis 的字段计算器工具也可以实现类似功能,但是需要自己写一段代码实现, 相对而言不是很方便。 如下所示,该工具就是【编辑】下的【属性】下的【按顺序编号】工具。 其操作方法是…...
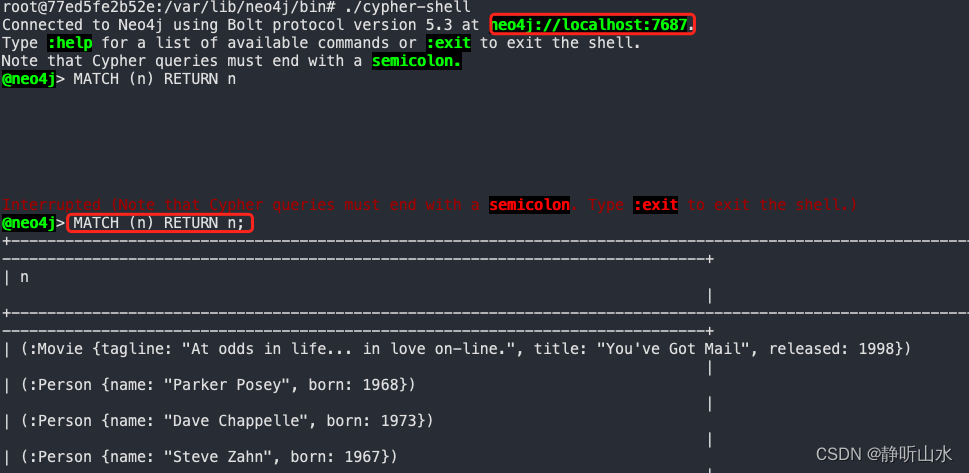
neo4j终端操作
1】进入容器 (base) xiaokkkxiaokkkdeMacBook-Pro ~ % docker exec -it 77ed5fe2b52e /bin/bash 2】启动、停止neo4j root77ed5fe2b52e:/var/lib/neo4j/bin# ./neo4j start Neo4j is already running (pid:7). Run with --verbose for a more detailed error message.root7…...
【深度学习】在 MNIST实现自动编码器实践教程
一、说明 自动编码器是一种无监督学习的神经网络模型,主要用于降维或特征提取。常见的自动编码器包括基本的单层自动编码器、深度自动编码器、卷积自动编码器和变分自动编码器等。 其中,基本的单层自动编码器由一个编码器和一个解码器组成,编…...
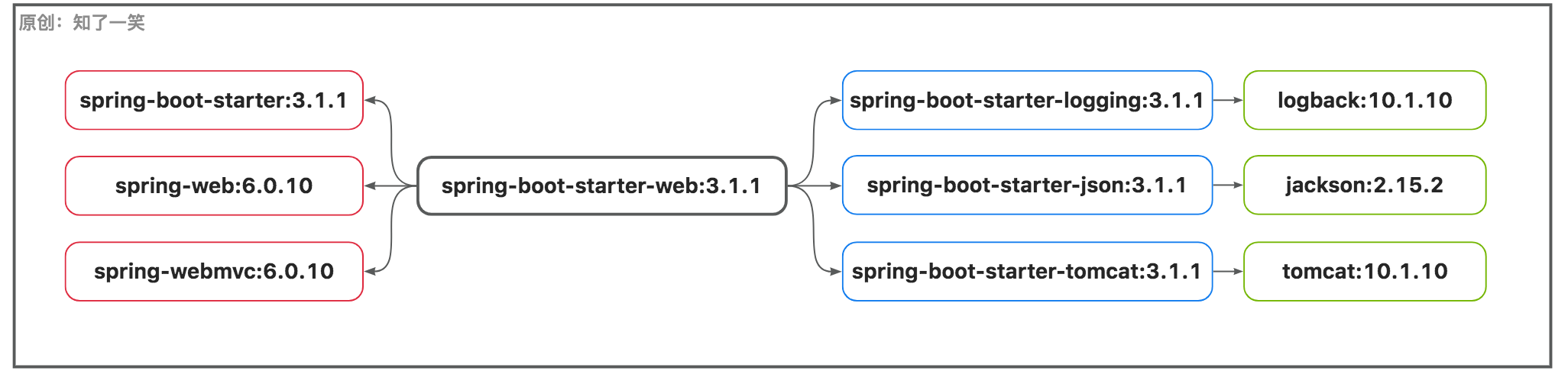
SpringBoot3基础用法
技术和工具「!喜新厌旧」 一、背景 最近在一个轻量级的服务中,尝试了最新的技术和工具选型; 即SpringBoot3,JDK17,IDEA2023,Navicat16,虽然新的技术和工具都更加强大和高效,但是适应采坑的过程…...

6、移除链表元素
方法1:原链表删除元素 伪代码: 首先判断头节点是否是待删除元素。(头节点和其他节点的删除方法不一样) while(head ! null && head->value target) //如果链表为 1 1 1 1 1,要删除元素1时用if就会失效 {h…...
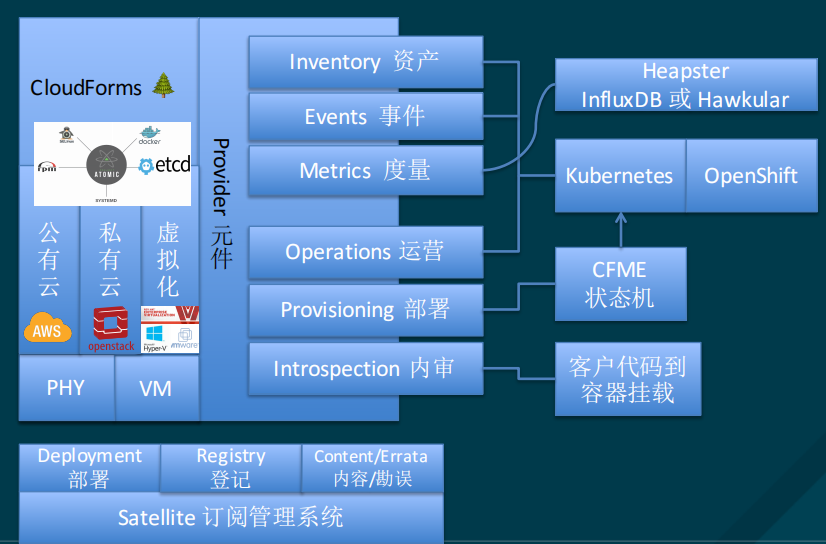
大厂容器云实践之路(一)
1-华为CCE容器云实践 华为企业云 | CCE容器引擎实践 ——从IaaS到PaaS到容器集群 容器部署时代的来临 IaaS服务如日中天 2014-2015年,大家都在安逸的使用IaaS服务; 亚马逊AWS的部署能力方面比所有竞争对手…...
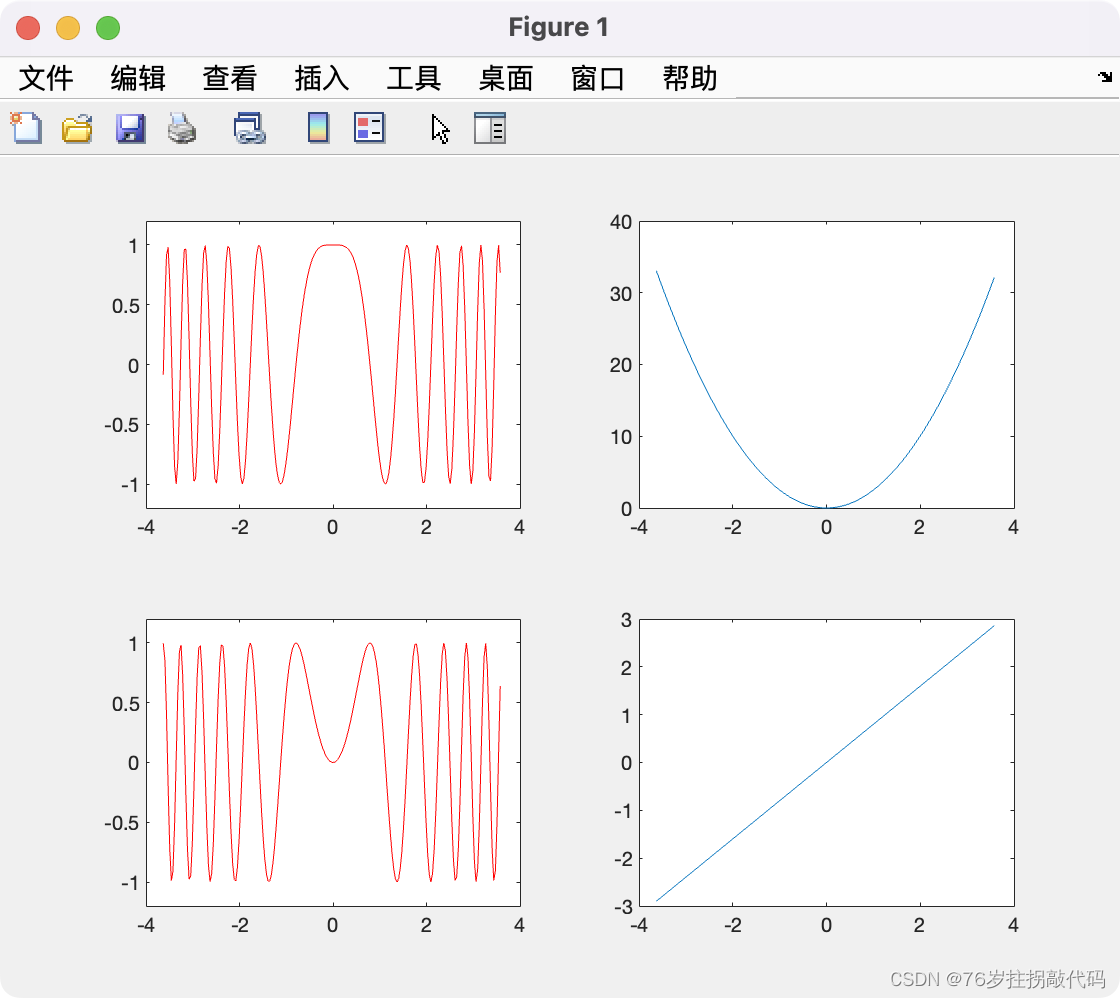
《合成孔径雷达成像算法与实现》Figure3.1
代码复现如下: clc close all clear all%参数设置 B 5.80e6; %信号带宽 T 7.26e-6; %脉冲持续时间 K B/T; %线性调频频率 alpha 5; %过采样率 F alpha*B; %采样频率 N F*T; %采样点数 dt T/N; …...
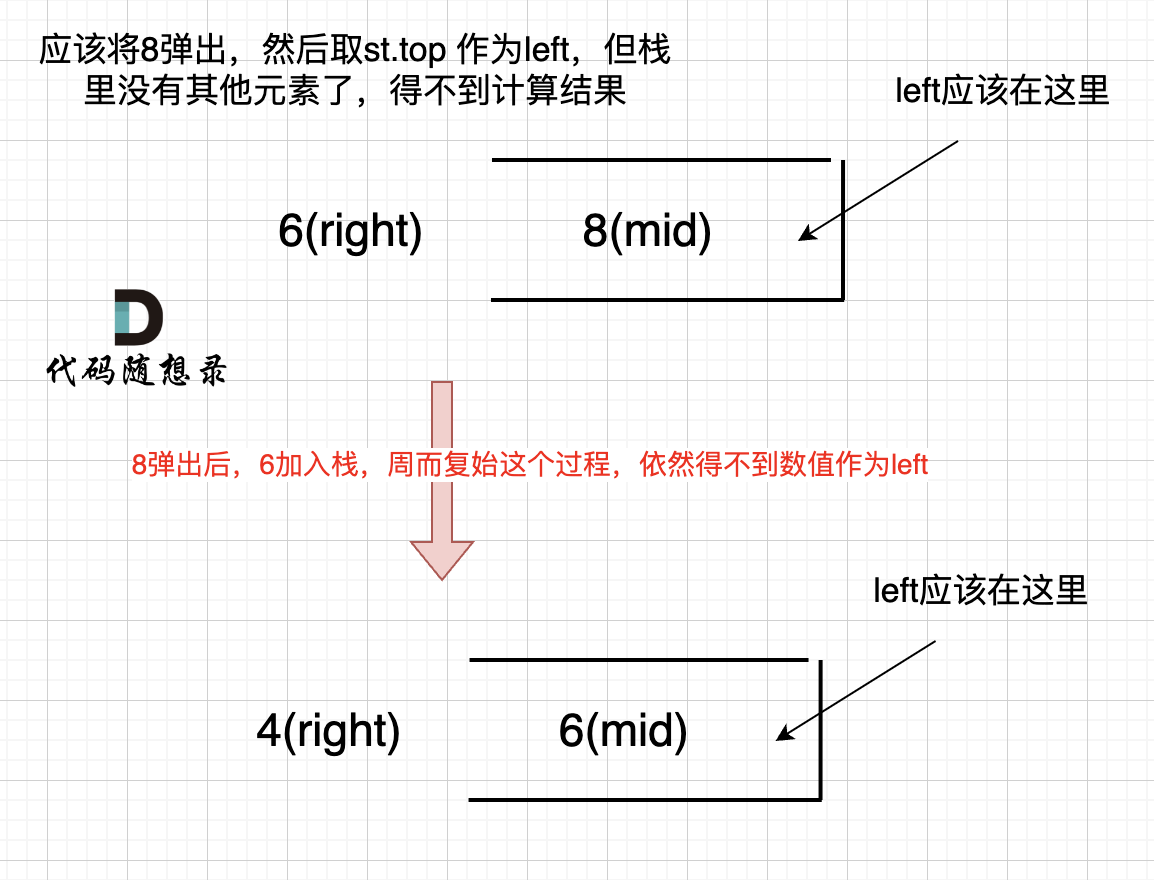
代码随想录算法训练营day60
文章目录 Day60 柱状图中最大的矩形题目思路代码 Day60 柱状图中最大的矩形 84. 柱状图中最大的矩形 - 力扣(LeetCode) 题目 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图…...
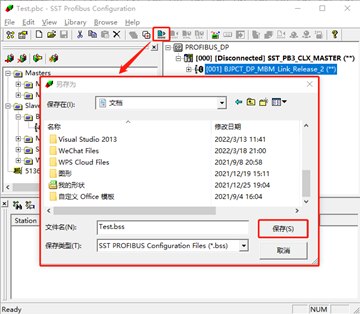
Modbus TCP转Profibus DP网关modbus tcp报文解析
捷米JM-DPM-TCP网关。在Profibus总线侧作为主站,在以太网侧作为ModbusTcp服务器功能, 下面是介绍捷米JM-DPM-TCP主站网关组态工具的配置方法 2, Profibus主站组态工具安装 执行资料光盘中的安装文件setup64.exe或setup.exe安装组态工具。安装过程中一直…...

对 Promise 的理解
Promise 是异步编程的一种解决方案,它是一个对象,可以获取异步 操作的消息,他的出现大大改善了异步编程的困境,避免了地狱回调, 它比传统的解决方案回调函数和事件更合理和更强大。 所谓 Promise,简单说就…...

Vuex:Vue.js应用程序的状态管理模式
介绍 在Vue.js应用程序中,随着项目复杂度的增加,组件之间的数据共享和管理变得困难。为了解决这个问题,Vue.js提供了一个名为Vuex的状态管理模式。Vuex可以帮助我们更有效地组织、管理和共享应用程序的状态。 什么是Vuex? Vuex…...
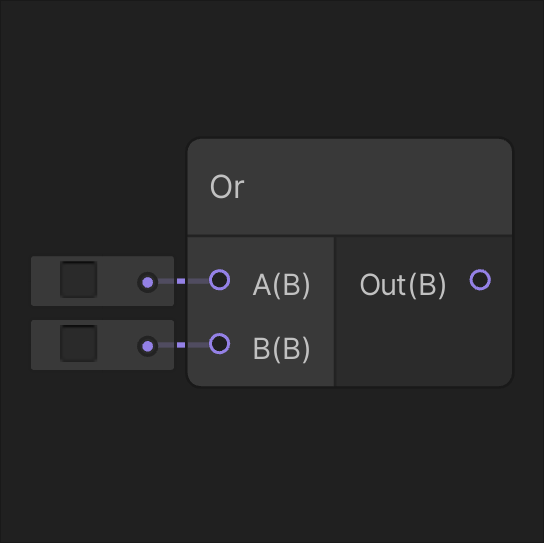
Unity之ShaderGraph 节点介绍 Utility节点
Utility 逻辑All(所有分量都不为零,返回 true)Any(任何分量不为零,返回 true)And(A 和 B 均为 true)Branch(动态分支)Comparison(两个输入值 A 和…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
:处理原始数据命令)
ffmpeg(三):处理原始数据命令
FFmpeg 可以直接处理原始音频和视频数据(Raw PCM、YUV 等),常见场景包括: 将原始 YUV 图像编码为 H.264 视频将 PCM 音频编码为 AAC 或 MP3对原始音视频数据进行封装(如封装为 MP4、TS) 处理原始 YUV 视频…...

AWSLambda之设置时区
目标 希望Lambda运行的时区是东八区。 解决 只需要设置lambda的环境变量TZ为东八区时区即可,即Asia/Shanghai。 参考 使用 Lambda 环境变量...

大模型智能体核心技术:CoT与ReAct深度解析
**导读:**在当今AI技术快速发展的背景下,大模型的推理能力和可解释性成为业界关注的焦点。本文深入解析了两项核心技术:CoT(思维链)和ReAct(推理与行动),这两种方法正在重新定义大模…...
