【周赛第69期】满分题解 软件工程选择题 枚举 dfs
目录
- 选择题
- 1.
- 2.
- 3.
- 4.
- 面向对象设计七大原则
- 编程题
- S数
- 最小H值
昨晚没睡好,脑子不清醒,痛失第1名
选择题
1.
关于工程效能,以下哪个选项可以帮助提高团队的开发效率?
A、频繁地进行代码审查
B、使用自动化测试工具
C、使用版本控制系统
D、所有选项都正确
选D。
2.
以下哪个选项不属于编码规范的内容?
A、变量命名规则
B、注释规范
C、代码缩进和格式化
D、数据库表设计
选D。
3.
以下哪个设计原则鼓励我们在实现功能时,尽量对现有代码进行扩展而不是修改?
A、单一职责原则
B、开放封闭原则
C、里氏替换原则
D、接口隔离原则
选B。
4.
关于软件架构设计,以下哪个原则可以帮助我们降低系统的耦合度?
A、单一职责原则
B、开放封闭原则
C、里氏替换原则
D、依赖倒置原则
选D。
面向对象设计七大原则
开闭原则、里氏代换原则、迪米特原则(最少知道原则)、单一职责原则、接口分隔原则、依赖倒置原则、组合/聚合复用原则。
编程题
S数
如果一个正整数 自身是回文数 ,而且它也是一个 回文数 的 平方,那么我们称这个数为 S数。 现在,给定两个正整数
L 和 R(以字符串形式表示),返回包含在范围 [L, R] 中的S数的数目。
我是按自身是回文数枚举的,其实应该按枚举量少的进行枚举,按开平方后的回文数枚举应该会更快。
为了代码简单写的快最后再检查范围。
#include<bits/stdc++.h>using namespace std;
using LL = long long;
LL L, R;
int strL[20], strR[20];
int topL, topR;
LL ans = 0;
int str[20];bool check(int x) {int s[20] = {};int len = 0;while (x) {s[++len] = x % 10;x /= 10;}for (int i = 1, j = len; i < j; i++, j--) {if (s[i] != s[j])return false;}return true;
}void dfs(LL now, int step, int base, int len) {if (step == base + 1) {if (len & 1) {for (int i = base - 1; i >= 1; i--) {now = now * 10 + str[i];}} else {for (int i = base; i >= 1; i--) {now = now * 10 + str[i];}}if (now < L)return;if (now > R) {cout << ans << endl;exit(0);}LL tmp = sqrt(now);if (tmp * tmp == now && check(tmp)) {++ans;}if ((tmp + 1) * (tmp + 1) == now && check(tmp + 1)) {//cout<<" "<<now<<endl;++ans;}return;}if (step == 1) {static const int f[] = {0, 1, 4, 5, 6, 9};for (int i = 0; i < 6; i++) {str[step] = f[i];dfs(now * 10 + f[i], step + 1, base, len);}} else {for (int i = 0; i <= 9; i++) {str[step] = i;dfs(now * 10 + i, step + 1, base, len);}}
}int main() {cin >> L >> R;for (int i = L; i; i /= 10) {strL[++topL] = i % 10;}for (int i = R; i; i /= 10) {strR[++topR] = i % 10;}for (int len = topL; len <= topR; len++) {int baseLen = (len + 1) / 2;dfs(0, 1, baseLen, len);}cout << ans << endl;return 0;
}最小H值
给你一个二维 rows x columns 的地图 heights , 其中 heights[row][col] 表示格子 (row,
col) 的高度。 一开始你在最左上角的格子 (0, 0) , 且你希望去最右下角的格子 (rows-1, columns-1)
(注意下标从 0 开始编号)。 你每次可以往 上,下,左,右 四个方向之一移动,你想要找到H值最小的一条路径。 一条路径的 H值
是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。 请你返回从左上角走到右下角的最小H值。
不是只能下、右,一开始想错了。
dfs需要注意避免不必要的重复,才能保证时间复杂度。
#include<bits/stdc++.h>using namespace std;
string mp;
int hang = -1;
int lie = 1;
vector<vector<int>> mpp;
vector<vector<int>> dis;inline char getChar() {static int pos = 0;if (pos == (int) mp.length()) {return EOF;}return mp[pos++];
}inline int getInt() {int x = 0;int f = 1;char t = getChar();while (t > '9' || t < '0') {if (t == '-')f = -1;t = getChar();}while (t >= '0' && t <= '9') {x = x * 10 + t - '0';t = getChar();}return x * f;
}const int f[4][2] = {{-1, 0},{0, -1},{0, 1},{1, 0}};bool dfs(int x, int y) {if (x == hang - 1 && y == lie - 1) {return true;}for (int i = 0; i < 4; i++) {int nx = x + f[i][0];int ny = y + f[i][1];if (nx < 0 || ny < 0 || nx >= hang || ny >= lie) { continue; }int newDis = max(dis[x][y], abs(mpp[x][y] - mpp[nx][ny]));if (dis[nx][ny] != -1 && dis[nx][ny] <= newDis) { continue; }dis[nx][ny] = newDis;//cout<<nx<<" "<<ny<<" : "<<newDis<<endl;dfs(nx, ny);}return true;
}int main() {cin >> mp;for (int i = 0; i < (int) mp.length(); i++) { if (mp[i] == '[') { ++hang; }}for (int i = 0; i < (int) mp.length(); i++) {if (mp[i] == ']') { break; }if (mp[i] == ',') { ++lie; }}mpp = vector<vector<int>>(hang, vector<int>(lie, 0));vector<vector<int>> dp = vector<vector<int>>(hang, vector<int>(lie, 0));dis = vector<vector<int>>(hang, vector<int>(lie, -1));for (int nowH = 0, nowL = 0; nowH <hang;) {mpp[nowH][nowL] = getInt();//cout<<nowH<<" "<<nowL<<" : "<<mpp[nowH][nowL]<<endl;++nowL;if (nowL == lie) {++nowH;nowL = 0;}}for (int i = 0; i < hang; i++) {for (int j = 0; j < lie; j++) {if (i == 0 && j == 0) {dp[i][j] = 0;} else if (i == 0) {dp[i][j] = max(dp[i][j - 1], abs(mpp[i][j] - mpp[i][j - 1]));} else if (j == 0) {dp[i][j] = max(dp[i - 1][j], abs(mpp[i][j] - mpp[i - 1][j]));} else {dp[i][j] = min(max(dp[i][j - 1], abs(mpp[i][j] - mpp[i][j - 1])),max(dp[i - 1][j], abs(mpp[i][j] - mpp[i - 1][j])));}}}dis[0][0] = 0;dfs(0, 0);cout << dis[hang - 1][lie - 1] << endl;return 0;
}
相关文章:

【周赛第69期】满分题解 软件工程选择题 枚举 dfs
目录 选择题1.2.3.4.面向对象设计七大原则 编程题S数最小H值 昨晚没睡好,脑子不清醒,痛失第1名 选择题 1. 关于工程效能,以下哪个选项可以帮助提高团队的开发效率? A、频繁地进行代码审查 B、使用自动化测试工具 C、使用版本控…...

P2015 二叉苹果树
P2015 二叉苹果树 类似于带限制背包问题,但不知道也能做。 n , q n,q n,q 范围小,大胆设 dp 状态。设 f u , i \large f_{u,i} fu,i 表示 u u u 子树内保留 i i i 根树枝的最大苹果数,可得状态转移方程 f u , i f u , j f v , i − …...

Linux 内核音频数据传递主要流程
Linux 用户空间应用程序通过声卡驱动程序(一般牵涉到多个设备驱动程序)和 Linux 内核 ALSA 框架导出的 PCM 设备文件,如 /dev/snd/pcmC0D0c 和 /dev/snd/pcmC0D0p 等,与 Linux 内核音频设备驱动程序和音频硬件进行数据传递。PCM 设…...

torch.device函数
torch.device 是 PyTorch 中用于表示计算设备(如CPU或GPU)的类。它允许你在代码中指定你希望在哪个设备上执行张量和模型操作,本文主要介绍了 torch.device 函数的用法和功能。 本文主要包含以下内容: 1.创建设备对象2.将张量和模…...
火车头采集器AI伪原创【php源码】
大家好,本文将围绕python作业提交什么文件展开说明,python123怎么提交作业是一个很多人都想弄明白的事情,想搞清楚python期末作业程序需要先了解以下几个事情。 火车头采集ai伪原创插件截图: I have a python project, whose fold…...

Python中常见的6种数据类型
数字(Numbers):数字类型用于表示数值,包括整数(int)和浮点数(float)。 字符串(Strings):字符串类型用于表示文本,由一系列字符组成。字…...
消息队列项目(2)
我们使用 SQLite 来进行对 Exchange, Queue, Binding 的硬盘保存 对 Message 就保存在硬盘的文本中 SQLite 封装 这里是在 application.yaml 中来引进对 SQLite 的封装 spring:datasource:url: jdbc:sqlite:./data/meta.dbusername:password:driver-class-name: org.sqlite.…...
解决MAC M1处理器运行Android protoc时出现的错误
Protobuf是Google开发的一种新的结构化数据存储格式,一般用于结构化数据的序列化,也就是我们常说的数据序列化。这个序列化协议非常轻量级和高效,并且是跨平台的。目前,它支持多种主流语言,比传统的XML、JSON等方法更具…...

C#使用SnsSharp实现鼠标键盘钩子,实现全局按键响应
gitee下载地址:https://gitee.com/linsns/snssharp 一、键盘事件,使用SnsKeyboardHook 按键事件共有3个: KeyDown(按键按下) KeyUp(按键松开) KeyPress(按键按下并松开) 以KeyDown事件为例,使用代码如下&…...

Zookeeper基础操作
搭建Zookeeper服务器 windows下部署 下载地址: https://mirrors.cloud.tencent.com/apache/zookeeper/zookeeper-3.7.1/ 修改配置文件 打开conf目录,将 zoo_sample.cfg复制一份,命名为 zoo.cfg打开 zoo.cfg,修改 dataDir路径,…...
【CSS】说说响应式布局
目录 一、是什么 二、怎么实现 1、媒体查询 2、百分比 3、vw/vh 4、小结 三、总结 一、是什么 响应式设计简而言之,就是一个网站能够兼容多个终端——而不是为每个终端做一个特定的版本。 响应式网站常见特点: 同时适配PC 平板 手机等…...
数据结构 | 利用二叉堆实现优先级队列
目录 一、二叉堆的操作 二、二叉堆的实现 2.1 结构属性 2.2 堆的有序性 2.3 堆操作 队列有一个重要的变体,叫作优先级队列。和队列一样,优先级队列从头部移除元素,不过元素的逻辑顺序是由优先级决定的。优先级最高的元素在最前ÿ…...

Javascript怎样阻止事件传播?
在 JavaScript 中,可以使用事件对象的方法来阻止事件传播。事件传播指的是当一个元素上触发了一个事件,该事件会在事件流中传播到父元素或祖先元素,从而影响到它们。 事件传播有三个阶段:捕获阶段、目标阶段和冒泡阶段。阻止事件…...
web-csrf
目录 CSRF与XSS的区别: get请求 原理: pikachu为例 post请求 pikachu为例 CSRF与XSS的区别: CSRF是借用户的权限完成攻击,攻击者并没有拿到用户的权限,而XSS是直接盗取到了用户的权限 get请求 原理:…...
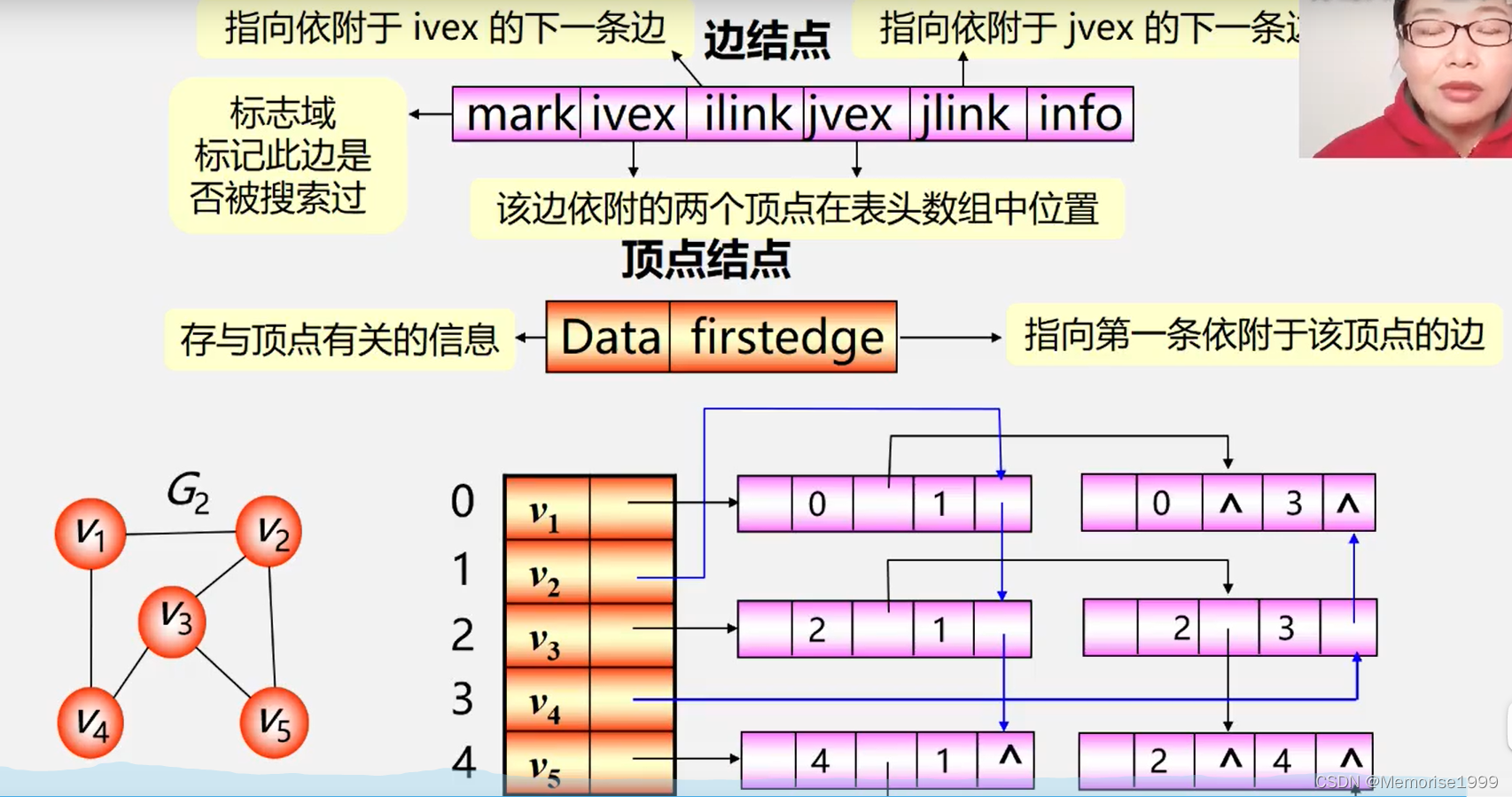
数据结构—图的存储结构
6.图 回顾:数据的逻辑结构 集合——数据元素间除 “同属于一个集合” 外,无其他关系。 线性结构——一个对一个,如线性表、栈、队列 树形结构——一个对多个,如树 图形结构——多个对多个,如图 6.1图的定义和术语 图:…...

Vue3 中 setup,ref 和 reactive 的理解
setup Vue3中使用了Composition API这种写法,使得所有的组合API函数都在此使用, 只在初始化时执行一次。 函数如果返回对象, 对象中的属性或方法, 模板中可以直接使用 ref 作用:定义一个数据的响应式 语法:const xxx ref(initValue) 一般用来…...

BL302嵌入式ARM控制器进行SQLite3数据库操作的实例演示
本文主要讲述了在钡铼技术BL302嵌入式arm控制器上运行 SQLite3 数据库的命令示例。SQLite3 是一个轻型的嵌入式数据库,不需要安装数据库服务器进程,占用资源低且处理速度快。 首先,需要将对应版本的 SQLite3 文件复制到设备的 /usr/ 目录下&…...
C++ 多线程:std::future
std::future std::future 简介示例1博客引用来源 std::future 简介 我们前面介绍的std::thread 是C11中提供异步创建多线程的工具,只能是异步运行任务,却无法获取任务执行的结果,一般都是依靠全局对象,全局对象在多线程下是及其不…...
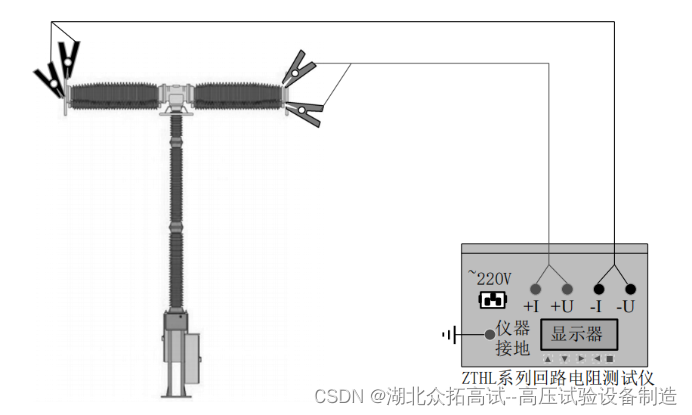
断路器回路电阻试验
试验目的 断路器回路电阻主要取决于断路器动、 静触头的接触电阻, 其大小直接影响正常 运行时的发热情况及切断短路电流的性能, 是反应安装检修质量的重要数据。 试验设备 回路电阻测试仪 厂家: 湖北众拓高试代销 试验接线 对于单断口的断路器, 通过断口两端的接线…...

Python中的CALL_FUNCTION指令
在Python字节码中,CALL_FUNCTION指令后跟的数字代表这次函数调用需要从栈上取出的参数的数量。具体来说,这个数字包括位置参数和关键字参数的数量。 这个数字的低两位表示位置参数的数量,然后每两位表示一个关键字参数的数量。因此ÿ…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
