AcWing《蓝桥杯集训·每日一题》—— 3777 砖块
AcWing《蓝桥杯集训·每日一题》—— 3777. 砖块
文章目录
- AcWing《蓝桥杯集训·每日一题》—— 3777. 砖块
- 一、题目
- 二、解题思路
- 三、解题思路
本次博客我是通过Notion软件写的,转md文件可能不太美观,大家可以去我的博客中查看:北天的 BLOG,持续更新中,另外这是我创建的编程学习小组频道,想一起学习的朋友可以一起!!!
一、题目
每个砖块要么是黑色的,要么是白色的。
现在你可以进行以下操作若干次(可以是 0 次):
选择两个相邻的砖块,反转它们的颜色。(黑变白,白变黑)
你的目标是通过不超过 3n3n3n 次操作,将所有砖块的颜色变得一致。
输入格式
第一行包含整数 TTT,表示共有 TTT 组测试数据。
每组数据第一行包含一个整数 nnn。
第二行包含一个长度为 nnn 的字符串 sss。其中的每个字符都是 W 或 B,如果第 iii 个字符是 W,则表示第 iii 号砖块是白色的,如果第 iii 个字符是 B,则表示第 iii 个砖块是黑色的。
输出格式
每组数据,如果无解则输出一行 −1。
否则,首先输出一行 kkk,表示需要的操作次数。
如果 k>0k>0k>0,则还需再输出一行 kkk 个整数,p1,p2,…,pkp1,p2,…,pkp1,p2,…,pk。其中 pip_ipi 表示第 iii 次操作,选中的砖块为 pip_ipi 和 pi+1p_i+1pi+1 号砖块。
如果方案不唯一,则输出任意合理方案即可。
数据范围
1≤T≤101≤T≤101≤T≤10,
2≤n≤2002≤n≤2002≤n≤200。
输入样例:
4
8
BWWWWWWB
4
BWBB
5
WWWWW
3
BWB
输出样例:
3
6 2 4
-1
0
2
2 1
二、解题思路
这道题目需要我们实现的是对给定字符串s进行操作,使得其变成一个全为’B’或全为’W’的字符串,并输出操作次数以及具体的操作。操作规则为,如果s中’B’和’W’个数均为偶数,则不需要进行任何操作;如果’B’个数为奇数,需要对相邻的两个’B’进行操作,使其变成’W’,或者将’B’和’W’对调,使得’B’个数变为偶数,然后进行相邻的’B’操作,使其变成’W’。如果’W’个数为奇数,操作方法与’B’个数奇数的情况相似。
具体来说,我们在实现的过程是先计算’B’和’W’的个数,然后根据个数的奇偶性进行分类讨论。当’B’和’W’的个数均为偶数时,不需要操作。当其中一个为奇数时,需要对相邻的两个颜色相同的块进行操作,使其变成相反的颜色,或者将两个不同颜色的块进行对调,使得颜色个数为偶数。通过循环操作后,最终得到一个全为’B’或者全为’W’的字符串。最后输出操作次数和具体操作的序列。
三、解题思路
# 输入测试用例数量
T = int(input())
for _ in range(T):# 输入字符串长度和字符串n = int(input())s = list(input())# 统计W和B的数量w_cnt = s.count('W')b_cnt = s.count('B')# 判断是否有解if w_cnt % 2 == 1 and b_cnt % 2 == 1:print(-1) # 没有解else:res_cnt = 0 # 记录需要操作的次数res = [] # 记录操作的位置if w_cnt % 2 == 1: # W的数量为奇数,需要将一些B变成Wi = 0while i < n - 1:if s[i] == 'B' and s[i+1] == 'B': # 连续的两个B都变成Ws[i] = 'W's[i+1] = 'W'res_cnt += 1res.append(i + 1)i += 2elif s[i] == 'B' and s[i+1] == 'W': # 只将前面的B变成Ws[i] = 'W's[i+1] = 'B'res_cnt += 1res.append(i + 1)i += 1elif s[i] == 'W': # 如果是W则不用操作i += 1else: # B的数量为奇数,需要将一些W变成Bi = 0while i < n - 1:if s[i] == 'W' and s[i+1] == 'W': # 连续的两个W都变成Bs[i] = 'B's[i+1] = 'B'res_cnt += 1res.append(i + 1)i += 2elif s[i] == 'W' and s[i+1] == 'B': # 只将前面的W变成Bs[i] = 'B's[i+1] = 'W'res_cnt += 1res.append(i + 1)i += 1elif s[i] == 'B': # 如果是B则不用操作i += 1# 输出结果if res_cnt > 0:print(res_cnt)for x in res:print(x, end = ' ')print()else:print(0)
这段代码的时间复杂度为O(Tn)O(Tn)O(Tn),其中TTT是测试用例的数量,nnn是输入字符串的长度。这是因为代码中有一个外层循环,循环TTT次,而每次循环中都要对长度为nnn的输入字符串进行遍历,所以总时间复杂度是O(Tn)O(Tn)O(Tn)。
在代码中,使用了一些内置函数和操作,如**s.count()和s[i]**等,这些操作的时间复杂度较低,可以忽略不计。因此,这段代码的主要瓶颈在于对输入字符串的遍历和修改操作。
如果要优化这段代码的时间复杂度,可能需要重新设计算法。可以考虑一些贪心策略,如将相邻的不同颜色的棋子互换,使得相邻的棋子颜色相同。这样可以尽可能地减少需要修改的棋子数量。但这个算法的正确性需要进行证明,同时实现也可能会比较复杂。
相关文章:

AcWing《蓝桥杯集训·每日一题》—— 3777 砖块
AcWing《蓝桥杯集训每日一题》—— 3777. 砖块 文章目录AcWing《蓝桥杯集训每日一题》—— 3777. 砖块一、题目二、解题思路三、解题思路本次博客我是通过Notion软件写的,转md文件可能不太美观,大家可以去我的博客中查看:北天的 BLOG…...

CleanMyMac X软件下载及详细功能介绍
mac平台的知名系统清理应用CleanMyMac在经历了一段时间的测试后,全新设计的X正式上线。与CleanMyMac3相比,新版本的UI设计焕然一新,采用了完全不同的风格。使用Windows电脑时,很多人会下载各类优化软件,而在Mac平台中&…...

pytorch零基础实现语义分割项目(一)——数据概况及预处理
语义分割之数据加载项目列表前言数据集概况数据组织形式数据集划分数据预处理均值与方差结尾项目列表 语义分割项目(一)——数据概况及预处理 语义分割项目(二)——标签转换与数据加载 语义分割项目(三)…...

ARM+LINUX嵌入式学习路线
嵌入式学习是一个循序渐进的过程,如果是希望向嵌入式软件方向发展的话,目前最常见的是嵌入式Linux方向,关注这个方向,大概分3个阶段: 1、嵌入式linux上层应用,包括QT的GUI开发 2、嵌入式linux系统开发 3、…...
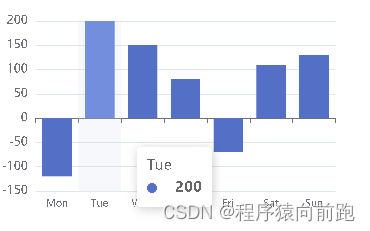
echart在微信小程序的使用
echart在微信小程序的使用 echarts不显示在微信小程序 <!-- 微信小程序的echart的使用 --> <view class"container"><ec-canvas id"mychart-dom-bar" canvas-id"mychart-bar" ec"{{ ec }}"></ec-canvas> &l…...
)
51单片机最强模块化封装(5)
文章目录 前言一、创建timer文件,添加timer文件路径二、timer文件编写三、模块化测试总结前言 今天这篇文章将为大家封装定时器模块,定时器是工程项目中必不可少的,希望大家能够将定时器理解清楚并且运用自如。 一、创建timer文件,添加timer文件路径 这里的操作就不过多…...

链表学习之判断链表是否回文
链表解题技巧 额外的数据结构(哈希表);快慢指针;虚拟头节点; 判断链表是否回文 要求:时间辅助度O(N),空间复杂度O(1) 方法1:栈(不考虑空间复杂度) 遍历一…...
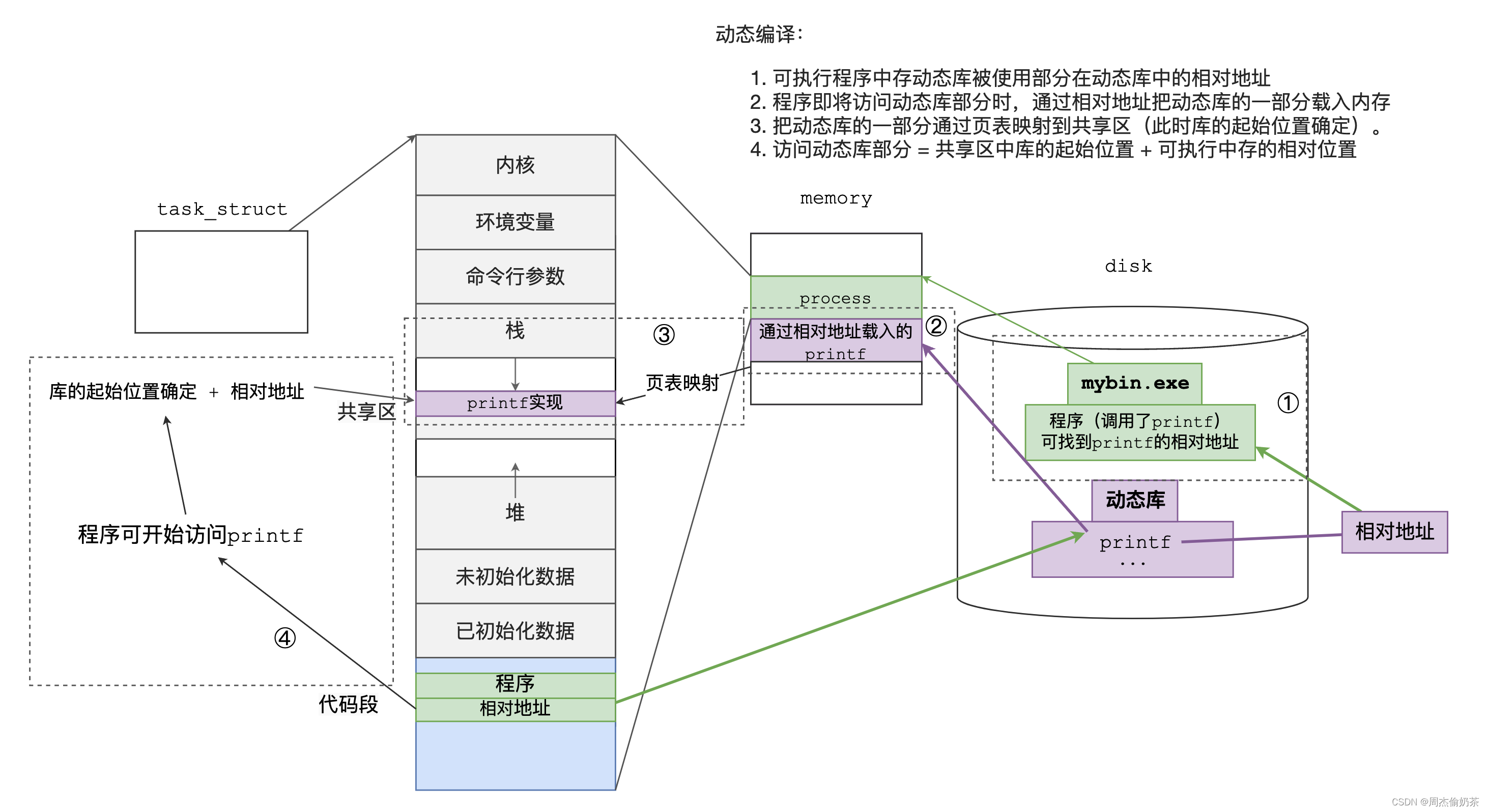
【Linux06-基础IO】4.5万字的基础IO讲解
前言 本期分享基础IO的知识,主要有: 复习C语言文件操作文件相关的系统调用文件描述符fd理解Linux下一切皆文件缓冲区文件系统软硬链接动静态库的理解和制作动静态编译 博主水平有限,不足之处望请斧正! C语言文件操作 #再谈文件…...

c++协程库理解—ucontext组件实践
文章目录1.干货写在前面2.ucontext初接触3.ucontext组件到底是什么4.小试牛刀-使用ucontext组件实现线程切换5.使用ucontext实现自己的线程库6.最后一步-使用我们自己的协程库1.干货写在前面 协程是一种用户态的轻量级线程 首先我们可以看看有哪些语言已经具备协程语义&#x…...

英语基础-状语
1. 课前引语 1. 形容词使用场景 (1). 放在系动词后面作表语 The boy is handsome. (2). 放在名词前面做定语 I like this beautiful girl. (3). 放在宾语后面做补语 You make your father happy. 总结:形容词无论做什么,都离不开名词,…...

目标检测笔记(八):自适应缩放技术Letterbox完整代码和结果展示
文章目录自适应缩放技术Letterbox介绍自适应缩放技术Letterbox流程自适应缩放Letterbox代码运行结果自适应缩放技术Letterbox介绍 由于数据集中存在多种不同和长宽比的样本图,传统的图片缩放方法按照固定尺寸来进行缩放会造成图片扭曲变形的问题。自适应缩放技术通…...

2023年全国最新高校辅导员精选真题及答案1
百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、选择题 11.李某与方某签订房屋租赁合同期间,李某欲购买租赁房屋ÿ…...

【Python】Python读写Excel表格
简要版,更多功能参考资料1。1 Excel文件保存格式基础概念此处不提,详见资料1。Excel的文件保存格式有两种: xls 和 xlsx。如果你看不到文件后缀,按下图设置可见。xls是Office 2003及之前版本的表格的默认保存格式。xlsx 是 Excel …...
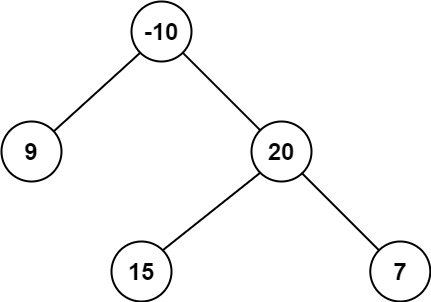
Python每日一练(20230218)
目录 1. 旋转图像 2. 解码方法 3. 二叉树最大路径和 1. 旋转图像 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像…...
基于SSM框架的狼途汽车门店管理系统的设计与实现
基于SSM框架的狼途汽车门店管理系统的设计与实现 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、…...

视频监控流程图3
<html> <head> <meta http-equiv"Content-Type" content"text/html; charsetUTF-8"/> <link rel"stylesheet" type"text/css" href"visio.css"/> <title> 视频监控流程图 </title> <…...
 2.14.3 CANFD协议介绍)
Linux ARM平台开发系列讲解(CAN) 2.14.3 CANFD协议介绍
1. 概述 前面章节介绍了CAN2.0协议,CAN现在主要是用在汽车领域,随着CAN的发展, 又衍生除了CANFD协议,该协议是在CAN的基础之上进行了升级,CAN2.0的最高速率是1Mbps,有限的速率导致CAN总线上负载率变高,所以CANFD就出现了,CANFD目前最高支持10Mbps。除此之外,CANFD还拥…...

参考 | 给C盘 “搬家“
参考 | 给C盘 “搬家” 将在C盘准备 “搬家” 的 文件/文件夹 完整路径 copy 下来 e.g. 路径一 “C:\Users\你的用户名\AppData\Roaming\kingsoft” 将这个 文件/文件夹 CTRLX 剪切下来 注意: 剪切后, 不需要自己重新新建, 直接执行第三步 将这个 文件/文件夹 CTRLV 粘贴到你要…...
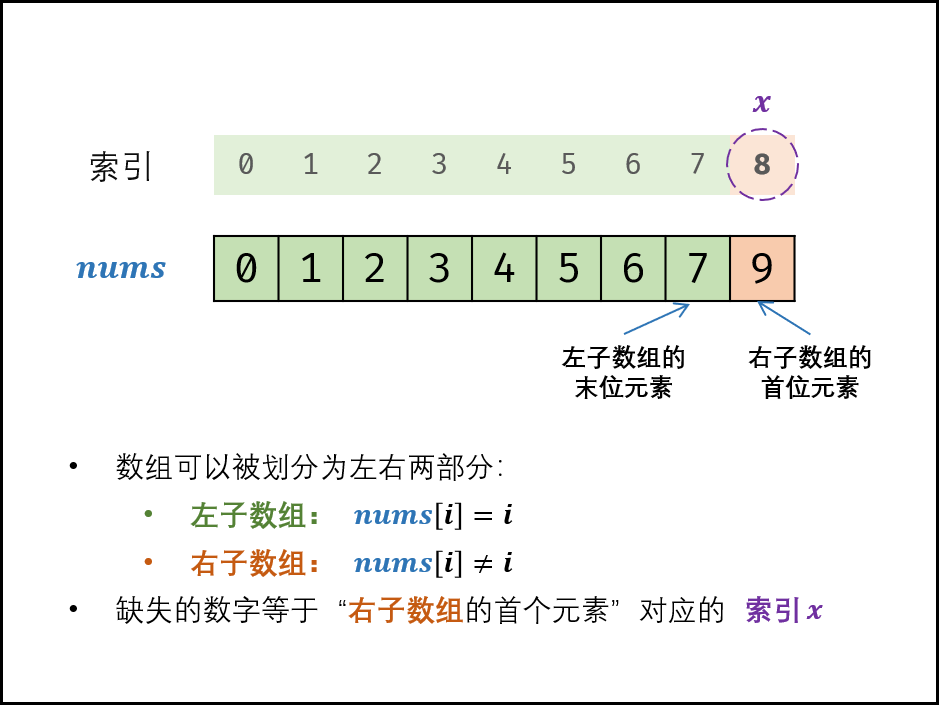
剑指 Offer 53 - II. 0~n-1中缺失的数字
原题链接 难度:easy\color{Green}{easy}easy 题目描述 一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字…...

分布式id
一、分布式系统 1.1 分布式系统的定义和应用场景 分布式系统是由多个独立的计算机节点协同工作,以共同完成一个任务的系统。这些节点通过网络进行通信和协调,共享计算和存储资源,从而实现对更大规模问题的处理和更高系统可用性的要求。 分…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
