数据结构之时间复杂度-空间复杂度
大家好,我是深鱼~
目录
1.数据结构前言
1.1什么是数据结构
1.2什么是算法
1.3数据结构和算法的重要性
1.4如何学好数据结构和算法
2.算法的效率
3.时间复杂度
3.1时间复杂度的概念
3.2大O的渐进表示法
【实例1】:双重循环的时间复杂度:O(N)
【实例2】:双重循环的时间复杂度:O(N+M)
【实例3】:常数循环的时间复杂度:O(1)
【实例4】:strchr的时间复杂度:O(N)
【实例5】:冒泡排序的时间复杂度:O(N^2)
【实例6】:二分查找的时间复杂度:O(log2N)
【实例7】:阶乘递归的时间复杂度:O(N)
【实例8】:斐波那契递归的时间复杂度:O(2^N)
4.空间复杂度
【实例1】:冒泡排序的空间复杂度:O(1)
【实例2】:斐波那契递归的空间复杂度:O(N)
【实例3】:函数阶乘递归的空间复杂度:O(N)
【拓展】递归版斐波那契数列的空间复杂度:O(N)
1.数据结构前言
1.1什么是数据结构
实现一些项目,需要在内存中将数据存储起来,数据结构就是计算机存储、组织数据的方式。指相互之间存在一种或多种特定关系的数据元素的集合。eg:数组,链表,树...
1.2什么是算法
算法简单来说就是一系列的计算步骤,用来将输入数据转化为输出结果的。常见的算法有:排序,查找,查重,推荐算法...
1.3数据结构和算法的重要性
在校招的笔试中会有很多有关数据结构和算法的题
可以看看链接,在未来工作中:
数据结构和算法对一个程序员来说的重要性
1.4如何学好数据结构和算法
<1>多敲代码
<2>注重画图和思考
2.算法的效率
算法的效率看两点,第一点看时间效率,也就是时间复杂度,第二点看空间效率,也就是空间复杂度,但是随着计算机行业的发展,计算机的存储容量已经达到了很高的程度,所以如今我们不用太关注一个算法的空间复杂度
3.时间复杂度
3.1时间复杂度的概念
算法的时间复杂度是数学里面一个带有未知数的函数表达式,算法的复杂度不是看这个算法的运行时间,因为环境不同,具体的运行时间就不一样,eg:10年前2核cpu、2g内存的机器和今天8核cpu、8g内存的机器,运行的时间就不一样。算法中的基本操作的执行次数,为算法的时间复杂度
3.2大O的渐进表示法
请计算一下Func1基本操作执行了多少次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{for (int j = 0; j < N ; ++ j){++count;}
}
for (int k = 0; k < 2 * N ; ++ k)
{++count;
}
int M = 10;
while (M--)
{++count;
}
printf("%d\n", count);
}Func1 执行的基本操作次数 :F(N)=N*N+2*N+10
当N = 10 F(N) = 130
当N = 100 F(N) = 10210
当N = 1000 F(N) = 1002010
N越大,后两项对结果的影响越小,所以实际计算时间复杂度时,我们只需要大概执行次数,那么这里我们使用大O的渐进表示法(估算),即时间复杂度:O(N^2)
大O渐进表示法:
(1)用常数1取代运行时间中的所有加法常数
(2)在修改后的运行次数函数中,只保留最高阶项
(3)如果最高阶存在且不是1,则取除与这个项目相乘的常数
【实例1】:双重循环的时间复杂度:O(N)
本来应该是2*N,根据大O渐进表示法(3)简化为O(N)
// 计算Func2的时间复杂度?
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}【实例2】:双重循环的时间复杂度:O(N+M)
(如果前提:M>>N,那么时间复杂度就是O(M);
N>>M,那么时间复杂度就是O(N);
M和N差不多,那么时间复杂度O(M)或O(N)都可以)
一般情况下时间复杂度计算时未知数都是用的N,但是也可以使用M,K等等其他的
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\n", count);
}
【实例3】:常数循环的时间复杂度:O(1)
本来是100,根据大O渐进表示法(1)简化为O(1)
(O(1)不是代表算法运行一次,而是常数次)
// 计算Func4的时间复杂度?
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}【实例4】:strchr的时间复杂度:O(N)
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character );strchr函数的逻辑实际就是下面这个
while(*str)
{
if(*str==character)
return str;
else
++str;
}
以hello world这个字符串为例:
假设查找的是h: 1 最好情况:任意输入规模的最小运行次数(下界)
假设查找的是w: N/2 平均情况:任意输入规模的期望运行次数(大概就是最好最坏相加/2)
假设查找的是d: N 最坏情况:任意输入规模的最大运行次数(上界)
当一个算法随着输入的不同,时间复杂度不同,时间复杂度做悲观预期,看最坏的情况(即这个例子的时间复杂度是O(N))
【实例5】:冒泡排序的时间复杂度:O(N^2)
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}时间复杂度:N-1,N-2,N-3...1 精确值也就是N*(N-1)/2,那么大O的渐变表示法就是O(N^2)
算时间复杂度不能只看几层循环,而要去看他的思想
【实例6】:二分查找的时间复杂度:O(log2N)
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
while (begin < end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid;
else
return mid;
}
return -1;
}最好的情况:O(1)
最坏的情况:O(log2N)
为什么是O(log2N)呢?
【画图理解】:假设我们要查找X次,一个数组的大小是N,每一次二分查找如果没有找到,N就除以2,考虑最坏的结果,那么直到N一直除到只剩1为止就结束了
N/2/2/2/2...=1
2^X=N
X=log2N
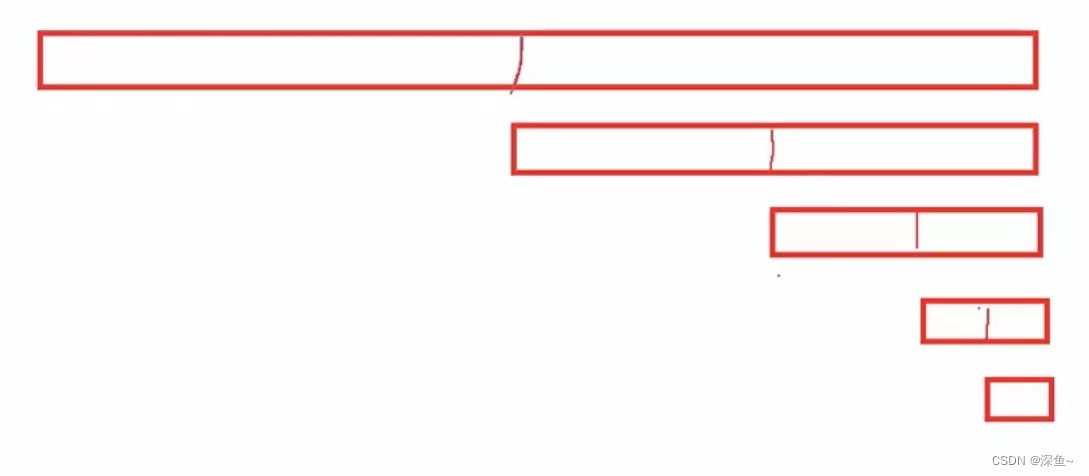
可见二分查找算法是一个非常牛逼的算法
N个数中查找 大概查找次数
1000 10
100W 20
10亿 30
但是这个算法的前提是数组有序
【实例7】:阶乘递归的时间复杂度:O(N)
递归算法时间复杂度:递归次数*每次递归调用的次数
// 计算阶乘递归Factorial的时间复杂度?
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}Fac(N) Fac(N-1) ... Fac(1)
【实例8】:斐波那契递归的时间复杂度:O(2^N)
// 计算斐波那契递归Fibonacci的时间复杂度?
long long Fibonacci(size_t N)
{
return N < 2 ? N : Fibonacci(N-1)+Fibonacci(N-2);
}【画图理解】:理解递归的逻辑思想,每一次递归都会调用小的两个递归,最后右边的递归调用会先结束,那么递归的次数就是等比数列的和减去右下角因提前结束而缺少的次数
Fib(N)=2^0+2^1+2^2+...+2^n-X
此处的每次递归调用的次数是个常数,就相当于没*
那么大O渐进表示法也就是O(2^N)
可见斐波那契数列的递归写法完全是一个没有实际用途的算法,因为太慢了

4.空间复杂度
空间复杂度也是一个数学表达式,是一个算法在运行过程中的临时额外占用存储空大小的量度
空间复杂度不是程序占用了多少bytes的空间,因为这个也没有太大的意义,所以空间复杂度算的是变量的个数
空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法
【注意】:函数运行时所需要的栈空间(存储参数,局部变量,一些存储器信息等等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时申请额外空间来确定
【实例1】:冒泡排序的空间复杂度:O(1)
冒泡排序中有三个变量:exchang,end,i,那么根据大O渐进表示法为O(1)
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}【实例2】:斐波那契递归的空间复杂度:O(N)
N个数的数组,动态开辟了N+1个空间,简化过后空间复杂度为O(N)
这个函数返回的是斐波那契数列的前n项的数组,而不是一个数
那个函数的时间复杂度为O(N),比递归的O(2^N)简化了很多
// 计算Fibonacci的空间复杂度?
//返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray =
(long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i ] = fibArray[ i - 1] + fibArray [i - 2];
}
return fibArray ;
}【实例3】:函数阶乘递归的空间复杂度:O(N)
// 计算阶乘递归Factorial的空间复杂度?
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}【画图理解】:递归函数调用了N次,开辟了N个栈帧,每个栈帧使用了常数的个空间,所以空间复杂度为O(N) (只要看递归的深度)
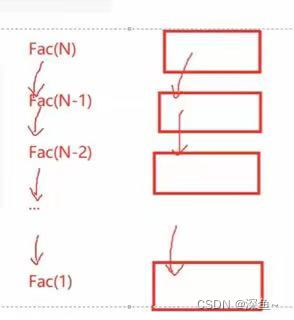
【拓展】递归版斐波那契数列的空间复杂度:O(N)
// 计算斐波那契递归Fibonacci的空间复杂度?
long long Fibonacci(size_t N)
{
return N < 2 ? N : Fibonacci(N-1)+Fibonacci(N-2);
}【画图理解】: 本函数调用空间的顺序是Fbi(N),Fbi(N-1)...Fbi(1),也就是最左边的一个枝干,然后这些函数的空间销毁,继续下一个枝干,这样函数递归的深度一直都是N,而不会是2^N
空间是可以重复利用,不累计的
时间是一去不复返,累积的

这次数据结构之时间和空间复杂度的内容就到此啦,有什么问题欢迎评论区或者私信交流,觉得笔者写的还可以,或者自己有些许收获的,麻烦铁汁们动动小手,给俺来个一键三连,万分感谢 !

相关文章:

数据结构之时间复杂度-空间复杂度
大家好,我是深鱼~ 目录 1.数据结构前言 1.1什么是数据结构 1.2什么是算法 1.3数据结构和算法的重要性 1.4如何学好数据结构和算法 2.算法的效率 3.时间复杂度 3.1时间复杂度的概念 3.2大O的渐进表示法 【实例1】:双重循环的时间复杂度…...

新一代构建工具 maven-mvnd
新一代构建工具 maven-mvnd mvnd的前世今生下载安装 mvndIDEA集成 mvnd的前世今生 maven 作为一代经典的构建工具,流行了很多年,知道现在依然是大部分Java项目的构建工具的首选;但随着项目复杂度提高,代码量及依赖库的增多使得ma…...
构建Docker容器监控系统(2)(Cadvisor +Prometheus+Grafana)
Cadvisor产品简介 Cadvisor是Google开源的一款用于展示和分析容器运行状态的可视化工具。通过在主机上运行Cadvisor用户可以轻松的获取到当前主机上容器的运行统计信息,并以图表的形式向用户展示。 接着上一篇来继续 部署Cadvisor 被监控主机上部署Cadvisor容器…...

Leetcode.995 K 连续位的最小翻转次数
题目链接 Leetcode.995 K 连续位的最小翻转次数 rating : 1835 题目描述 给定一个二进制数组 n u m s nums nums 和一个整数 k k k 。 k k k位翻转 就是从 n u m s nums nums 中选择一个长度为 k k k 的 子数组 ,同时把子数组中的每一个 0 0 0 都改成 1 1 1 …...

PHP8的跳转语句-PHP8知识详解
如果循环条件满足的时候,则程序会一直执行下去。如果需要强制跳出循环,则需要使用跳转语句来完成。PHP8的跳转语句包括break语句、continue语句和goto语句。 1、break语句 break语句的作用是完全终止循环,包括while、do…while、for、switch…...

Idea中maven无法下载源码
今天在解决问题的时候想要下载源码,突然发现idea无法下载,这是真的蛋疼,没办法查看原因,最后发现问题的原因居然是因为Maven,由于我使用的idea的内置的Bundle3的Maven,之前没有研究过本地安装和内置的区别&…...
【linux-keepalive】keepalive避免单点故障,高可用配置
keepalive: [rootproxy ~]# yum install -y keepalived [rootproxy ~]# vim /etc/keepalived/keepalived.conf global_defs {router_id proxy1 //设置路由ID号vrrp_iptables //不添加任何防火墙规则 } vrrp_instance V…...

测试网络模型的FLOPs和params
概念 FLOPS:注意全大写,是floating point operations per second的缩写,意指每秒浮点运算次数,理解为计算速度。是一个衡量硬件性能的指标。 FLOPs:注意s小写,是floating point operations的缩写…...

《树莓派项目实战》第十五节 使用L298N驱动板模块驱动双极42步进电机
目录 15.1 双极步进电机引脚介绍 15.2 连接到树莓派 15.3 编写代码驱动步进电机 在本节,我们将学习如何使用L298N驱动板驱动一个双极42步进电机。该项目涉及到的材料有: 树莓派...
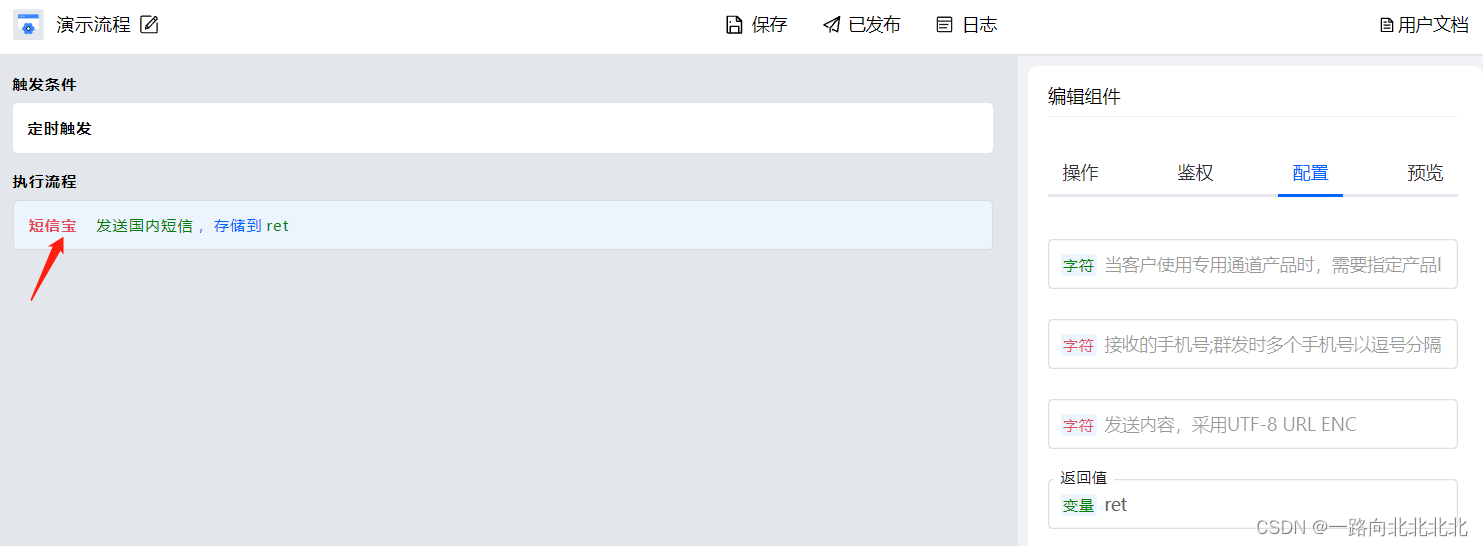
基于短信宝API零代码实现短信自动化业务
场景描述: 基于短信宝开放的API能力,实现在特定事件(如天气预警)或定时自动发送短信(本文以定时群发短信为例)。通过Aboter平台如何实现呢? 使用方法: 首先创建一个IPaaS流程&…...
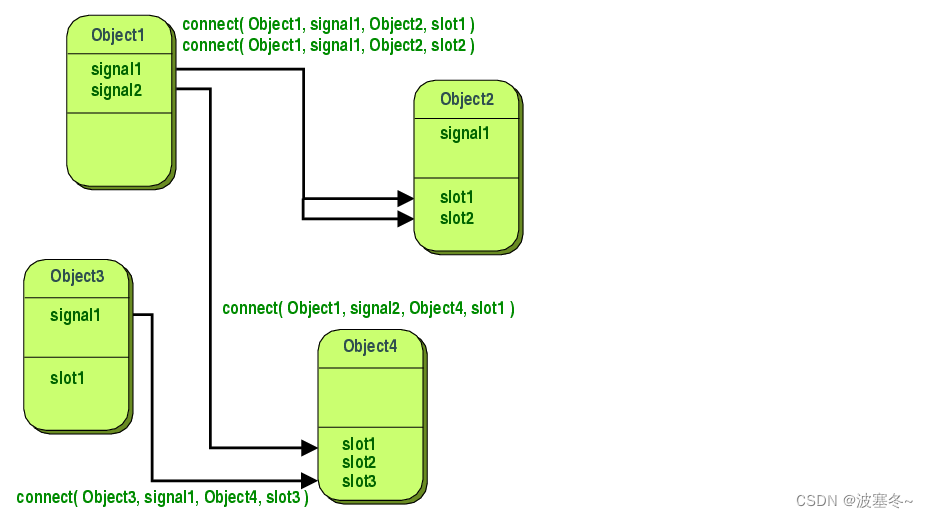
Qt应用开发(基础篇)——信号槽 Signals and Slots
一、前言 Qt成为我们今天拥有的灵活而舒适的工具,除了友好和能够快速开发设计师界面,信号槽机制是最大的核心特征,也是区别于其他开发框架最大的优势。 Qt的信号槽作用于两个对象之间的通信。当一个对象发生了改变,它希望其他关心…...

正则表达式--Notepad++常用的替换
原文网址:正则表达式--Notepad常用的替换_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Notepad使用正则表达式进行替换时的常用的一些示例。 服务器JSON的格式化 例1:将回车去掉,改为正确的JSON格式 搜索: ([^,])(\r)(\n)(\s) 替…...

ES6 对象合并
对象合并 在 JavaScript 中,可以使用不同的方法来合并对象的属性。这样可以将两个或多个对象的属性合并到一个新的对象中。这是在编程中常见的一种操作,尤其在处理配置、选项或数据更新时非常有用。 以下是几种常见的对象合并方法: 1. 使用…...
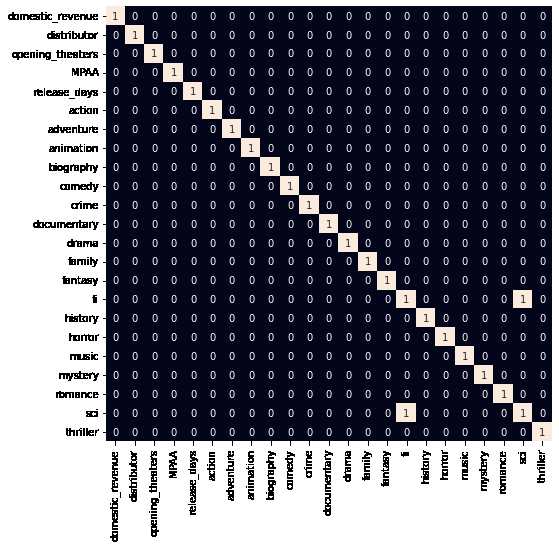
使用线性回归预测票房收入 -- 机器学习项目基础篇(10)
当一部电影被制作时,导演当然希望最大化他/她的电影的收入。但是我们能通过它的类型或预算信息来预测一部电影的收入会是多少吗?这正是我们将在本文中学习的内容,我们将学习如何实现一种机器学习算法,该算法可以通过使用电影的类型…...

一文读懂|RDMA原理
什么是DMA DMA全称为Direct Memory Access,即直接内存访问。意思是外设对内存的读写过程可以不用CPU参与而直接进行。我们先来看一下没有DMA的时候: 无DMA控制器时I/O设备和内存间的数据路径 假设I/O设备为一个普通网卡,为了从内存拿到需要…...
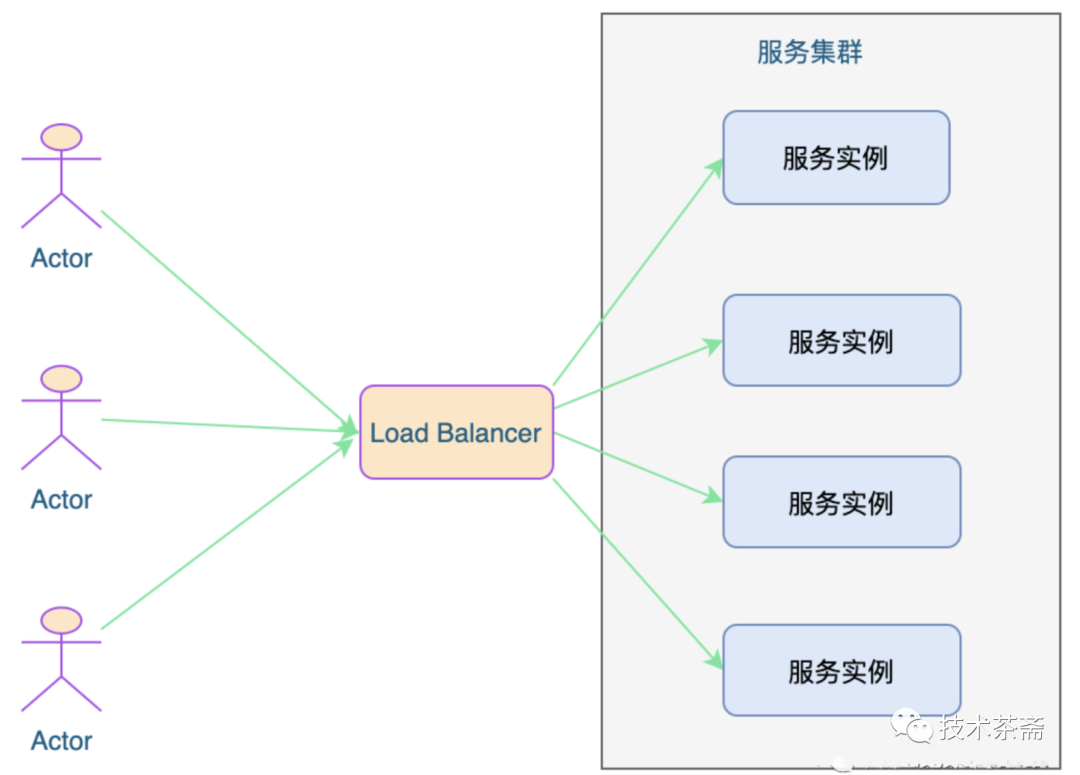
深入理解负载均衡原理及算法
1. 前言 在互联网早期,网络还不是很发达,上网用户少,流量相对较小,系统架构以单体架构为主。但如今在互联网发达的今天,流量请求动辄百亿、甚至上千亿,单台服务器或者实例已完全不能满足需求,这就有了集群。不论是为了实现高可用还是高性能,都需要用到多台机器来扩展服…...
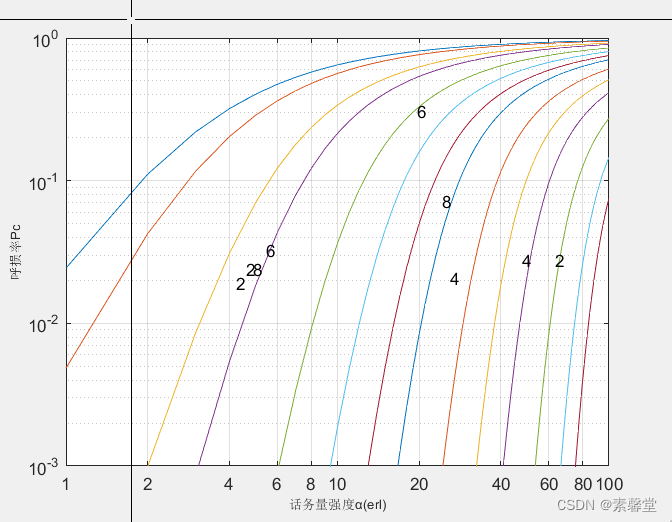
44.实现爱尔兰B公式计算并输出表格(matlab程序)
1.简述 1.话务量定义 话务量指在一特定时间内呼叫次数与每次呼叫平均占用时间的乘积。 话务量反映了电话负荷的大小,与呼叫强度和呼叫保持时间有关。呼叫强度是单位时间内发生的呼叫次数,呼叫保持时间也就是占用时间。 话务量计算方法 话务量公式为…...

【Linux】-- 进程间通信
目录 一、进程间通信介绍 二、管道 1.什么是管道(pipe) 2.重定向和管道 (1)为什么要有管道的存在 (2)重定向和管道的区别 3.匿名管道 (1)匿名管道原理 (2&…...

[PyTorch][chapter 48][LSTM -3]
简介: 主要介绍一下 sin(x): 为 数据 cos(x): 为对应的label 项目包括两个文件 main.py: 模型的训练,验证,参数保存 lstm.py 模型的构建 目录: lstm.py main.py 一 lstm.py # -*- coding: utf-8 -*- "&q…...

xss csrf 攻击
介绍 xss csrf 攻击 XSS: XSS 是指跨站脚本攻击。攻击者利用站点的漏洞,在表单提交时,在表单内容中加入一些恶意脚本,当其他正常用户浏览页面,而页面中刚好出现攻击者的恶意脚本时,脚本被执行,从…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
