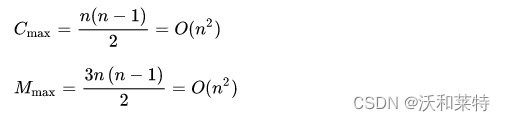PHP学习笔记(一谦四益)
前言
上一篇文章 PHP学习笔记(观隅反三)分享了数组的知识,这篇文章接着分享和数组相关的算法。
算法效率
算法效率分为两种:第一种是时间效率,第二种是空间效率。时间效率被称为时间复杂度,而空间效率被称作空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度,而空间复杂度主要衡量一个算法所需要的额外空间。
冒泡排序
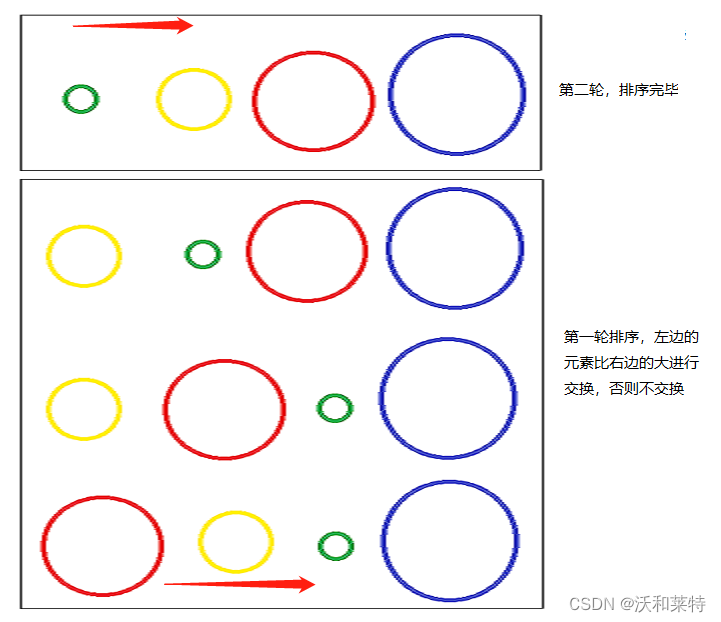
冒泡排序算法的原理如下:
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
$arr1=array(1,2,4,3,5,0,8);
for($j=0;$j<count($arr1);$j++){for($i=0;$i<count($arr1)-1-$j;$i++){if($arr1[$i]>$arr1[$i+1]){$temp=$arr1[$i];$arr1[$i]=$arr1[$i+1];$arr1[$i+1]=$temp;}}
}
echo '<pre>';
print_r($arr1);
//Array ( [0] => 0 [1] => 1 [2] => 2 [3] => 3 [4] => 4 [5] => 5 [6] => 8 )
时间复杂度
若文件的初始状态是正序的,一趟扫描即可完成排序。所需的
关键字比较次数C和记录移动次数M均达到最小值:Cmin=n-1 ; Mmin=0 ;
所以,冒泡排序最好的时间复杂度为O(n) 。
若初始文件是反序的,需要进行 n-1 趟排序。每趟排序要进行 n-i 次关键字的比较(1≤i≤n-1),且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下,比较和移动次数均达到最大值:
冒泡排序的最坏时间复杂度为 O(n2)。
综上,因此冒泡排序总的平均时间复杂度为 O(n2)。 [1]
稳定性
冒泡排序就是把小的元素往前调或者把大的元素往后调。
比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,是不会再交换的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
选择排序
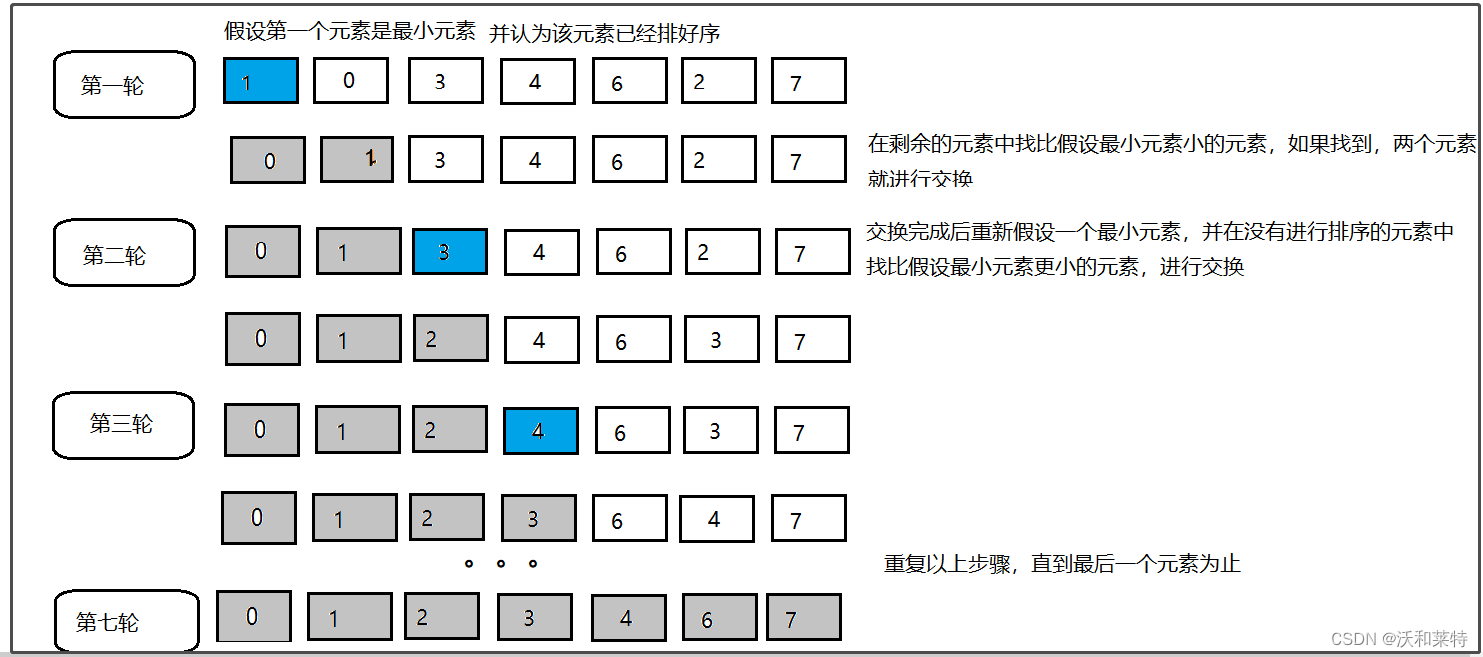
选择排序原理如下:
第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
$arr2=array(1,0,3,4,6,2,7);
for($i=0;$i<count($arr2);$i++){// 选定一个元素下标,假定其为最小元素下标,将其存储在变量$min中$min=$i;for($j=$i+1;$j<count($arr2);$j++){if($arr2[$j]<$arr2[$min]){$min=$j;}}// 如果选定的最小值不等于实际最小值,就进行交换if($min !=$i){$temp =$arr2[$i];$arr2[$i]=$arr2[$min];$arr2[$min]=$temp;}
}
print_r($arr2);
//Array ( [0] => 0 [1] => 1 [2] => 2 [3] => 3 [4] => 4 [5] => 6 [6] => 7 )
时间复杂度
选择排序的交换操作介于
0 和 (n - 1)次之间。选择排序的比较操作为n (n - 1) / 2次之间。选择排序的赋值操作介于 0 和 3 (n - 1) 次之间。比较次数O(n^2),比较次数与关键字的初始状态无关,总的比较次数N=(n-1)+(n-2)+…+1=n*(n-1)/2。交换次数O(n),最好情况是,已经有序,交换0次; 最坏情况交换n-1次,逆序交换n/2次。 交换次数比冒泡排序少多了,由于交换所需CPU时间比比较所需的CPU时间多,n值较小时,选择排序比冒泡排序快。
稳定性
在一趟选择,如果一个元素比当前元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。因此选择排序是一个
不稳定的排序算法。
插入排序
插入排序:
通常称之为 直接插入排序, 当进行少量数据的排序中,还可以使用插入排序的方法,插入排序的方法是将一个数据插入到已经排好序的有序数据中,以此得到一个新的个数加一的数组,该方法比较稳定。
$arr3=array(1,0,3,4,6,2,7);
for($i=1,$len=count($arr3);$i<$len;$i++){// 选出要插入元素$temp = $arr3[$i];//选出有序数列,将待插入元素和有序数列进行比较,若前者比后者小,就将待插入元素插入到指定位置,待插入元素后的原有序数列往后移,补上待插入元素的空位for($j=$i-1;$j>=0;$j--){if($arr3[$j]>$temp){$arr3[$j+1]=$arr3[$j];$arr3[$j]=$temp;}else{// 如果当前需要插入的元素要比前面的元素大,位置正确跳出循环break;}}
}
print_r($arr3);
//Array ( [0] => 0 [1] => 1 [2] => 2 [3] => 3 [4] => 4 [5] => 6 [6] => 7 )
时间复杂度
在插入排序中,当
待排序数组是有序时,此时是最优情况,即只需要和前一个数比较即可,这时比较只需要进行一次,时间复杂度是O(N);
最坏的情况是待排序数组是逆序的,此时需要比较的次数是最多的,即插入排序最坏情况的时间复杂度是 O(N2);
通常情况下,插入排序在平均情况下运行时间和最坏情况运行时间一样。
空间复杂度
插入排序的空间复杂度是
常数阶 O(1)。
稳定性
如果待排序的序列中存在
两个或两个以上具有相同关键词的数据,排序后这些数据的相对次序保持不变,即如果排序后两个相同的数的相对顺序不会发生改变,则该算法是稳定的;
如果排序后,数据的相对次序发生了变化,则该算法是不稳定的。关键词相同的数据元素将保持原有位置不变,所以该算法是稳定的。
归并排序
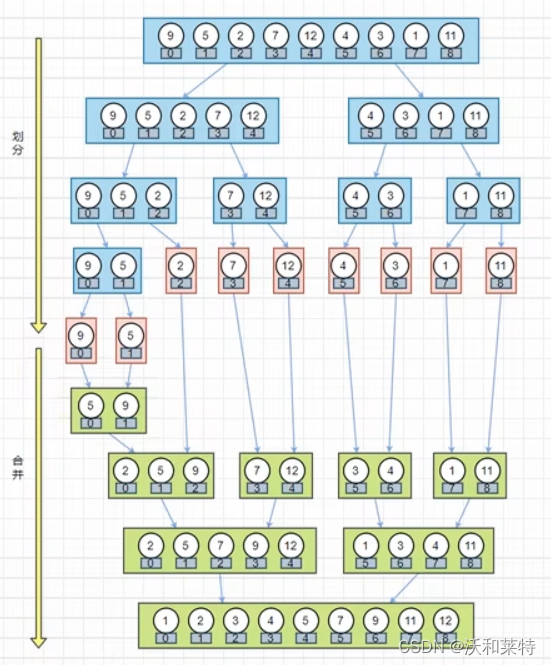
归并排序的原理:
将数组拆成两个数组;申请一个空间用于存放合并后的数组;
假设两个数组已经排好序列,设置两个指针,指针指向的位置分别是两个已经排好序的有序数列的数组的起始位置;
两指针分别指向两个数组的起始元素,并比较两个指针所指的元素,将较小的元素放入申请的空间;
然后将指针移动到下一位置;最后将另一个序列所剩的元素直接复制到合并序列中。
二路归并
$nums1=array(1,3,5);
$nums2=array(2,4,6);
// 申请空间用于存放合并后的数组
$nums3=array();
// 当需要合并的数组中含有元素,就进入循环
while(count($nums1) && count($nums2)){// 取出每个数组的第一个元素进行比较:array_shift() 函数删除数组中的第一个元素,并返回被删除元素的值。$nums3[]=$nums1[0]<$nums2[0]?array_shift($nums1):array_shift(($nums2));
}
// array_merge() 将一个或多个数组的单元合并起来,一个数组中的值附加在前一个数组的后面。返回作为结果的数组。
print_r(array_merge($nums3,$nums2,$nums1));//其中$nums1 $num2的顺序可颠倒
Array ( [0] => 1 [1] => 2 [2] => 3 [3] => 4 [4] => 5 [5] => 6 )
归并排序
通过二路归并的例子,归并排序就更容易理解了:
$arr4=array(2,4,1,3,6,5,0);function merge($arr4){$len=count($arr4);if($len<=1) return $arr4;$mid=floor($len/2);
// array_slice() 函数返回数组中的选定部分。$left=array_slice($arr4,0,$mid);$right=array_slice($arr4,$mid);// 如果分成的两个数组没有排好序,由于是奇数个元素的数组,无法均分成两个相同元素个数的数组// 最后在进行二路合并的时候就会乱序,因此需要对$left $right进行排序// 调用merge函数 $left=merge($left);$right=merge($right);$arr5=array();while(count($left) && count($right)){$arr5[]=$left[0]<$right[0]?array_shift($left):array_shift($right);}return array_merge($arr5,$left,$right);
}
print_r(merge($arr4));
//Array ( [0] => 0 [1] => 1 [2] => 2 [3] => 3 [4] => 4 [5] => 5 [6] => 6 )
时间复杂度
归并排序比较占用内存,但却是一种
效率高且稳定的算法。
改进归并排序在归并时先判断前段序列的最大值与后段序列最小值的关系再确定是否进行复制比较。如果前段序列的最大值小于等于后段序列最小值,则说明序列可以直接形成一段有序序列不需要再归并,反之则需要。所以在序列本身有序的情况下时间复杂度可以降至O(n)。
稳定性
归并排序是
稳定的排序.即相等的元素的顺序不会改变
查找算法
顺序查找
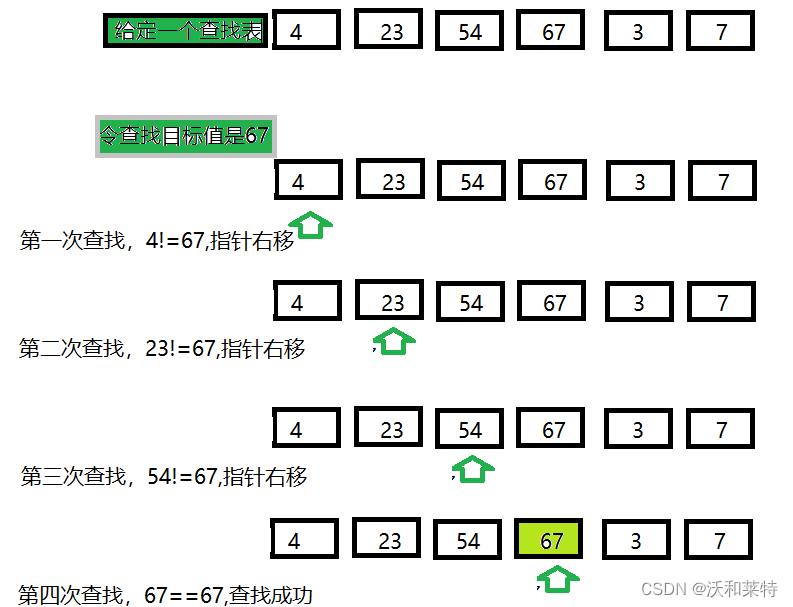
顺序查找也叫做线性查找,对于任意一个序列以及一个给定的元素,将
给定元素与序列中元素依次比较,直到找出与给定关键字相同的元素,或者将序列中的元素与其都比较完为止。
$arr2=array(4,23,54,67,3,7);
function check($arr2,$num){for($i=0;$i<count($arr2);$i++){if($arr2[$i]==$num){return $arr2[$i];}}return false;
}
var_dump(check($arr2,3));
//int(3)
二分查找算法
//二分查找$arr=array(1,4,2,3,6,5,7);//得到数组边界$right = count ($arr);$left = 0;$res = 3;//循环匹配while($left <= $right){//得到中间位置$middle = floor(($right - $left) /2);//进行查找匹配if($arr[$middle] == $res){echo $middle + 1;break;}if($arr[$middle]<$res{$left =$middle + 1;}else{$right=$middle - 1;}}
最后
以上就是这篇文章给大家带来的全部内容了,后续会持续更新相关文章,期待和大家的交流~
如有不足,感谢指正!
相关文章:
PHP学习笔记(一谦四益)
前言 上一篇文章 PHP学习笔记(观隅反三)分享了数组的知识,这篇文章接着分享和数组相关的算法。 算法效率 算法效率分为两种:第一种是时间效率,第二种是空间效率。时间效率被称为时间复杂度,而空间效率被称…...
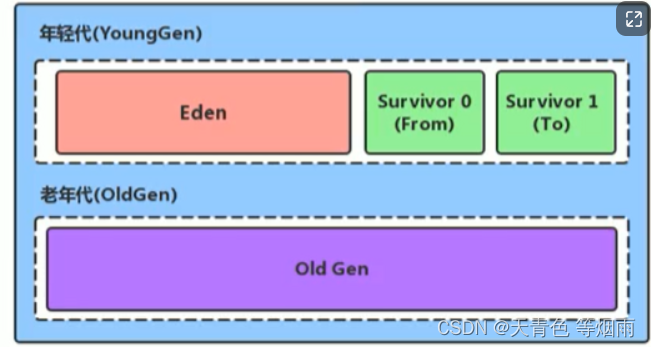
Jvm -堆对象的划分
堆对于一个jvm进程来说是唯一的,一个进程只有一个jvm,但是进程半酣多个线程,多个线程共享一个堆。 也就是说,一个jvm实例只存在一个堆,同时对也是Java内存管理的核心区域。 Java堆区域的大小在jvm启动时就已经被确定…...
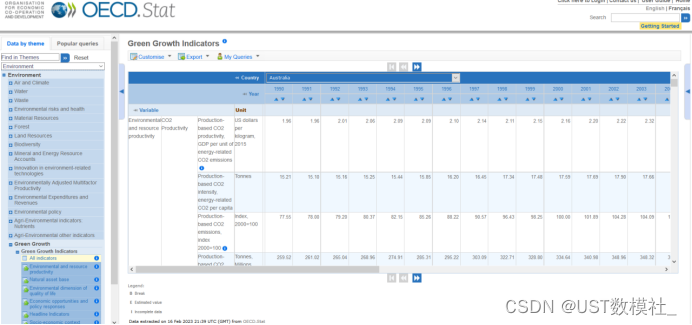
2023美赛F题讲解+数据领取
我们给大家准备了F题的数据,免费领取!在文末 国内生产总值(GDP)可以说是一个国家经济健康状况最著名和最常用的指标之--。它通常用于确定一个国家的购买力和获得贷款的机会,为各国提出提高GDP的政策和项目提供动力。GDP“衡量一个国家在给定时间段内生产…...

【博客625】keepalived开启garp refresh的重要性
keepalived开启garp refresh的重要性 1、场景 1-1、对keepavlied master机器热迁移后出现vip不通,过后恢复 原因:机器迁移后网关那边的arp表没有刷新,流量还是转发到老的端口,但是机器已经迁移到别的端口了,于是网络…...

nginx防护规则,拦截非法字符,防止SQL注入、防XSS,nginx过滤url访问,屏蔽垃圾蜘蛛,WordPress安全代码篇
nginx防护规则,拦截非法字符,防止SQL注入、防XSS,nginx过滤url访问,屏蔽垃圾蜘蛛,WordPress安全代码篇 精心强化,小白一键复制 资源宝分享:www.httple.net 宝塔为例:/www/server/panel/vhost/nginx/你的网站域名.conf,复制代码点击保存 修改www.xx.net你自己域名incl…...

【计算机网络】网络层
文章目录网络层概述网络层提供的两种服务IPv4地址IPv4地址概述分类编址的IPv4地址划分子网的IPv4地址无分类编址的IPv4地址IPv4地址的应用规划IP数据报的发送和转发过程静态路由配置及其可能产生的路由环路问题路由选择路由选择协议概述路由信息协议RIP的基本工作原理开放最短路…...

产品经理知识体系:1.什么是互联网思维?
互联网思维 思考 笔记 用户思维 是要注重用户体验,产品带给用户的价值是什么,是能帮助用户获取想要的商品、解决生活中的问题、获取想要的信息,还是产品能通过兜售参与感、满足感等来满足用户的心理需求。 贯穿产品的整个生命周期过程。 简…...

【数据结构】单链表的接口实现(附图解和源码)
单链表的接口实现(附图解和源码) 文章目录单链表的接口实现(附图解和源码)前言一、定义结构体二、接口实现(附图解源码)1.开辟新空间2.头插数据3.头删数据4.打印整个单链表5.尾删数据6.查找单链表中的数据7…...
TikTok话题量超30亿,这款承载美好记忆的剪贴簿引发讨论
回忆风剪贴簿在TikTok引起关注小超在浏览超店有数后台时发现,有一款平平无奇的剪贴簿的种草视频爆火,在24h内收获了9.9K点赞,播放量更是突破了100W,直接冲到了【种草视频飙升榜】第六名的位置,并且这个数字目前仍在继续…...

了解Dubbo
1.注册中心挂了,消费者还能不能调用生产者? 注册中心挂了, 消费者依然可以调用生产者。生产者和消费者都会在本地缓存注册中心的服务列表,当注册中心宕机时,消费者会读取本地的缓存数据,直接访问生产者&am…...
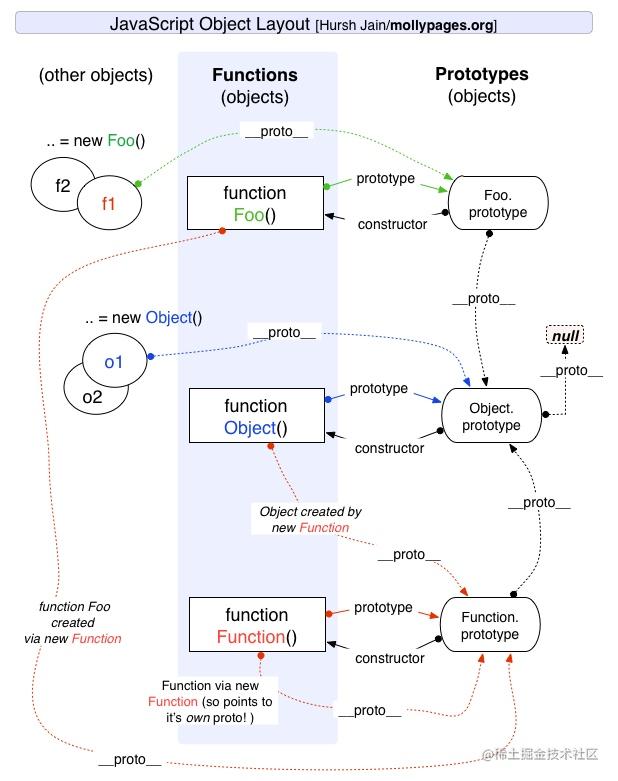
2023年前端面试知识点总结(JavaScript篇)
近期整理了一下高频的前端面试题,分享给大家一起来学习。如有问题,欢迎指正! 1. JavaScript有哪些数据类型 总共有8种数据类型,分别是Undefined、Null、Boolean、Number、String、Object、Symbol、BigInt Null 代表的含义是空对象…...

jQuery
文章目录jQuery 介绍初体验核心函数jQuery 对象和 dom 对象区分什么是 jQuery 对象,什么是 dom 对象问题:jQuery 对象的本质是什么?jQuery 对象和 Dom 对象使用区别Dom 对象和 jQuery 对象互转(重点)jQuery 选择器&…...

强化学习基础概念
强化学习入门 入门学习第一周:基础概念 经验回放: 将sss,agent当前步的action环与境的交互rrr以及下一步的状态st1s_{t1}st1组成的四元组[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wxhVd0dn-1676710992983)(null)] 组…...
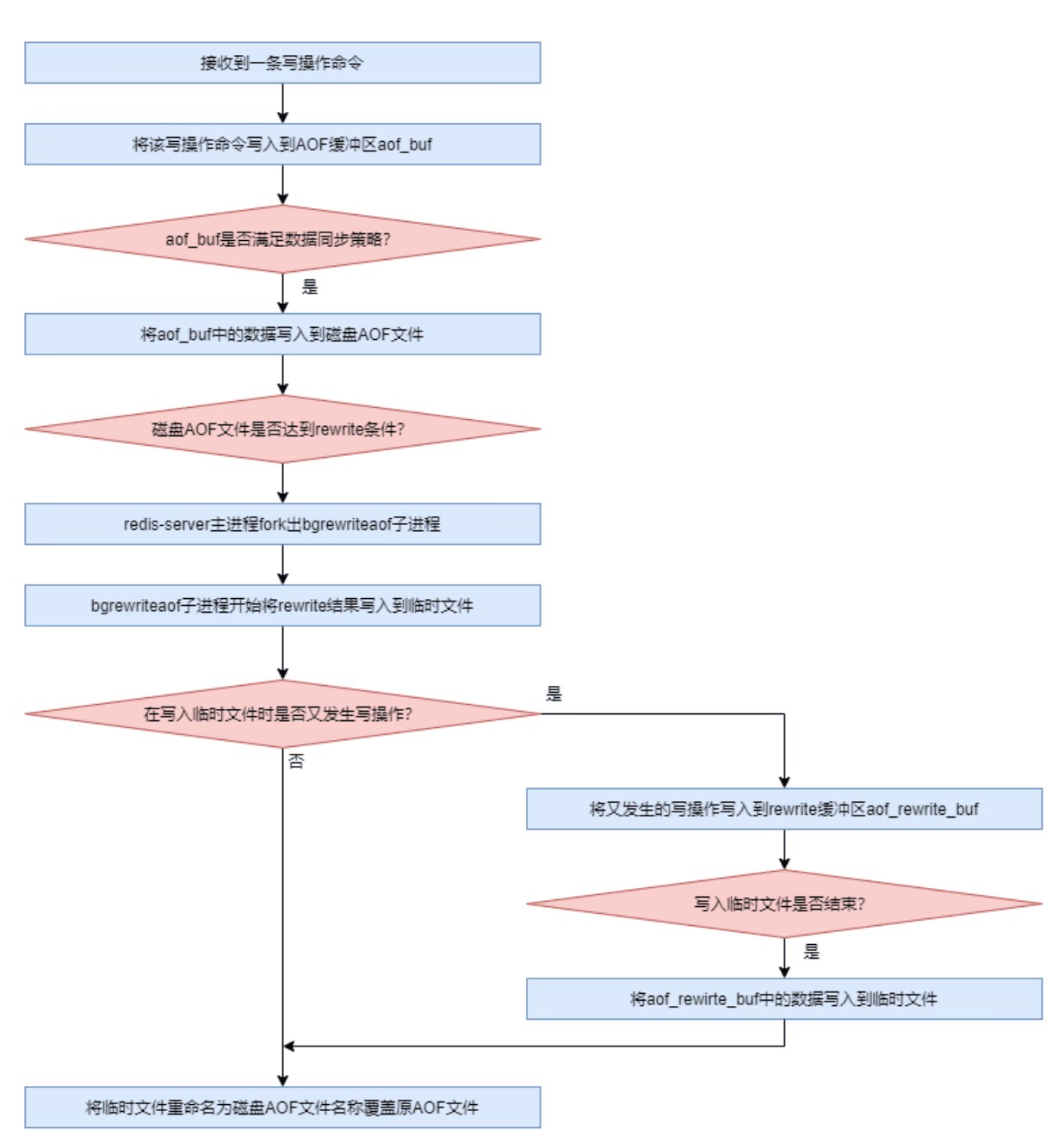
Redis学习【9】之Redis RDB持久化
文章目录一 AOF(Append Only File) 持久化二 AOF 基础配置2.1 AOF的开启2.2 文件名配置2.3 混合式持久化开启2.4 AOF 文件目录配置三 AOF 文件格式3.1 Redis 协议3.2 查看 AOF 文件3.3 清单文件3.4 Rewrite 机制3.4.1 rewrite简介3.4.2 rewrite 计算策略3.4.3 手动开启 rewrite…...

分析 vant4 源码,学会用 vue3 + ts 开发毫秒级渲染的倒计时组件,真是妙啊
2022年11月23日首发于掘金,现在同步到公众号。11. 前言大家好,我是若川。推荐点右上方蓝字若川视野把我的公众号设为星标。我倾力持续组织了一年多源码共读,感兴趣的可以加我微信 lxchuan12 参与。另外,想学源码,极力推…...
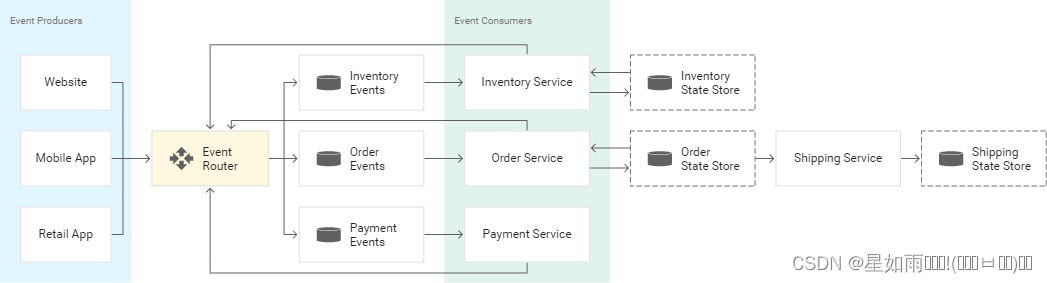
事件驱动型架构
事件驱动型架构是一种软件设计模式,其中微服务会对状态变化(称为“事件”)作出反应。事件可以携带状态(例如商品价格或收货地址),或者事件也可以是标识符(例如,订单送达或发货通知&a…...
)
20222023华为OD机试 - 不含 101 的数(Python)
不含 101 的数 题目 小明在学习二进制时,发现了一类不含 101 的数, 也就是将数字用二进制表示,不能出现 101 。 现在给定一个正整数区间 [l,r],请问这个区间内包含了多少个不含 101 的数? 输入 输入一行,包含两个正整数 l l l, r r r...

杭州电子科技大学2023年MBA招生考试成绩查询和复查申请的通知
根据往年的情况,2023杭州电子大学MBA考试初试成绩可能将于2月21日公布,最早于20号出来,为了广大考生可以及时查询到自己的分数,杭州达立易考教育为大家汇总了信息。根据教育部和浙江省教育考试院关于硕士研究生招生考试工作的统一…...
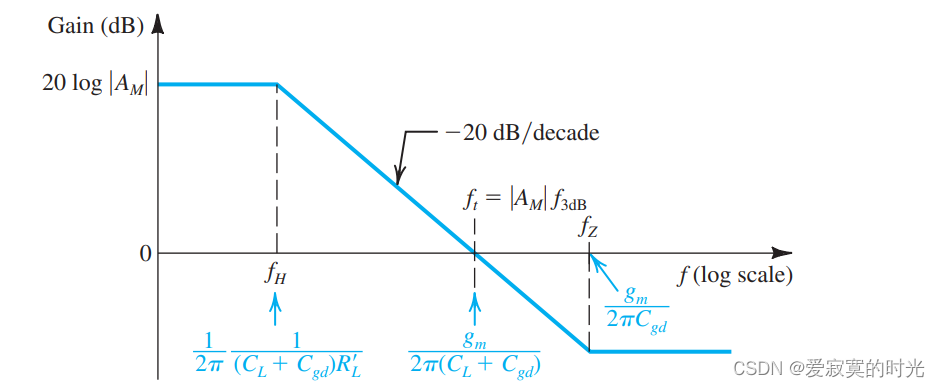
电子技术——CS和CE放大器的高频响应
电子技术——CS和CE放大器的高频响应 在绘制出MOS和BJT的高频响应模型之后,我们对MOS和BJT的高频响应有了进一步的认识。现在我们想知道的是在高频响应中 fHf_HfH 的关系。 高频响应分析对电容耦合还是直接耦合都是适用的,因为在电容耦合中高频模式下…...

2023年数学建模美赛D题(Prioritizing the UN Sustainability Goals):SDGs 优先事项的选择
正在写,不断更新,别着急。。。 4. SDGs 优先事项的选择 4.1 基于SDG密度分布图选择优先事项 虽然每个可持续发展目标的接近度矩阵和中心性度量的结果是通用的,并创建了基本的可持续发展目标网络,但由于各国在网络的不同部分取得…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...