455. 分发饼干、376. 摆动序列、53. 最大子数组和
455.分发饼干
题目描述:
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
解答:
法一:base实现
题目要求是尽可能满足孩子的数量最多
如果将大饼干分给胃口小的孩子,那么后面遇到胃口大的孩子就无法满足
因此可以先按照孩子胃口进行排序(便于后边用饼干匹配孩子胃口)
采用贪心算法,每次满足胃口最接近饼干尺寸(<=)的孩子
这样最终可以找到最优解
代码实现:
依次遍历饼干,同时还需要一个函数用于匹配胃口
class Solution {
public://找到最合适的孩子int findChild(vector<int>& g, int size){int location = -1;for (int i = 0; i < g.size(); i++){if (g[i] <= size)location = i;elsereturn location;}return location;}int findContentChildren(vector<int>& g, vector<int>& s) {int child_num = g.size() - 1;int fill_num = 0;//便于寻找最合适的孩子,可提前跳出循环sort(g.begin(), g.end());for (int i = 0; i < s.size(); i++){int location = findChild(g, s[i]);if(location != -1){g.erase(g.begin() + location);fill_num++;}}return fill_num;}
};法二:一重循环即可
为了满足更多的小孩,就不要造成饼干尺寸的浪费。
大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子,那么就应该优先满足胃口大的。
这里的局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩。
可以尝试使用贪心策略,先将饼干数组和小孩数组排序。
然后从后向前遍历小孩数组,用大饼干优先满足胃口大的,并统计满足小孩数量。
// 时间复杂度:O(nlogn)
// 空间复杂度:O(1)
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(), g.end());sort(s.begin(), s.end());int index = s.size() - 1; // 饼干数组的下标int result = 0;for (int i = g.size() - 1; i >= 0; i--) { // 遍历胃口 if (index >= 0 && s[index] >= g[i]) { // 遍历饼干 result++;index--;}}return result;}
};376.摆动序列
题目描述
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如, [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ,因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
相反,[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
解析:
乍一看,摆动序列+最长子序列,毫无思路。
仔细想想摆动序列,一正一负,就是要求是锯齿状,不满足条件的不要统计,反正本题并不要求返回序列,只要求返回长度,那其实比较简单了,用curDiff和preDiff分别统计差值,再使用一个条件判断即可:
if ((preDiff > 0 && curDiff < 0) || (preDiff < 0 && curDiff > 0))本题其实难点在于考虑各种各样的边界问题:
(1)只有两个的情况
可以直接返回2,为方便整合在一起,把初始的result设置为1即可
(2)有平坡的情况
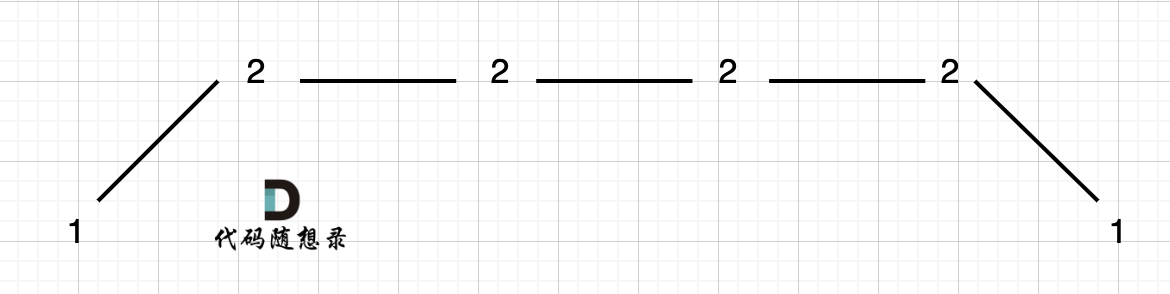
相等的时候不要记录,那修改判断条件为:
if ((preDiff >= 0 && curDiff < 0) || (preDiff <= 0 && curDiff > 0)){
同时这样修改条件也解决了首尾两端的问题
(3)单调有平坡
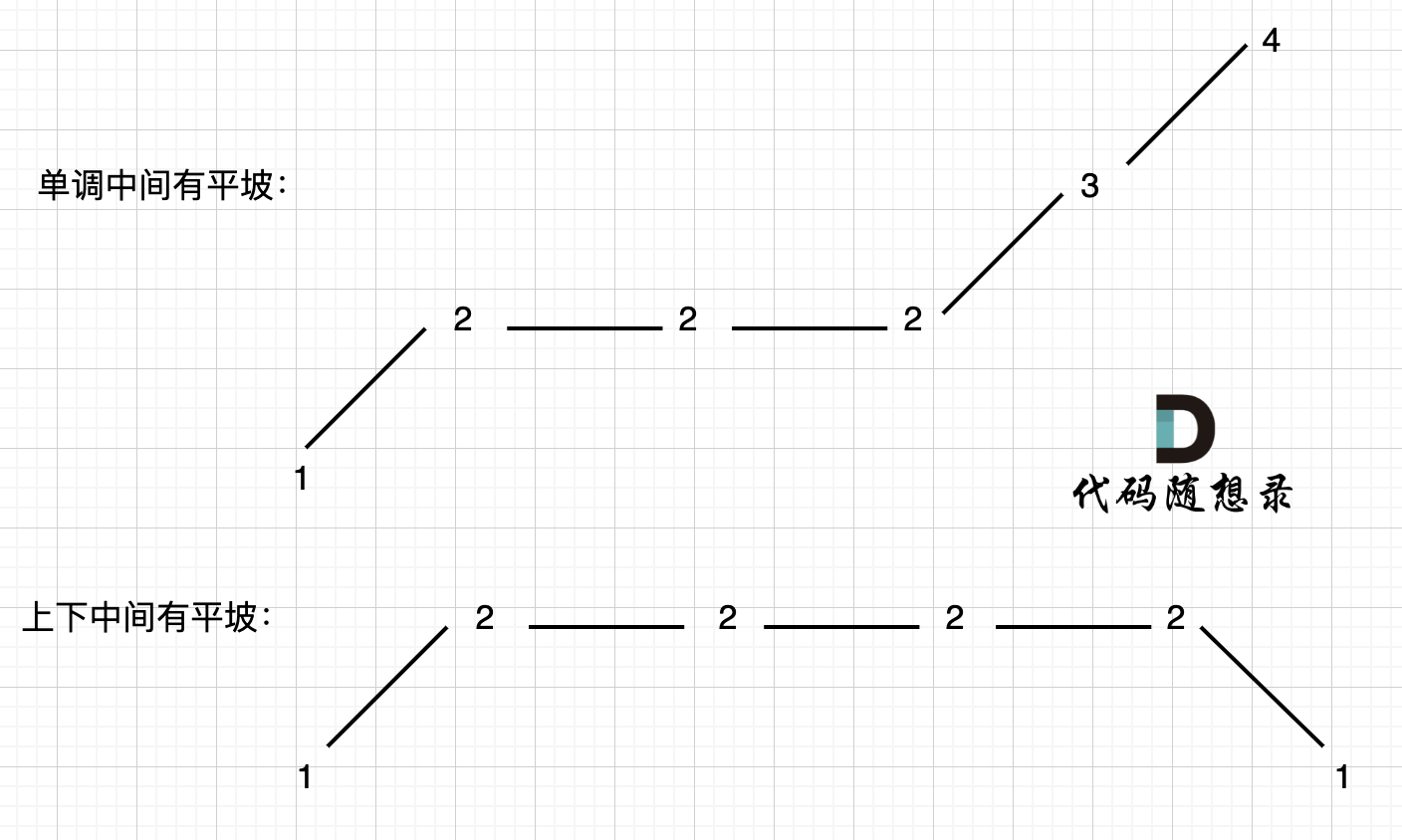
原来我是每次都会更新preDiff,但在这种情况下,到2-2-3时,明明不符合要求,但是preDiff=0,curDiff>0,错误统计
因此改为符合条件才去更新preDiff
代码实现如下:
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if (nums.size() <= 1)return nums.size();int curDiff = 0;int preDiff = 0;int result = 1;for (int i=0; i < nums.size() - 1; i++){curDiff = nums[i+1] - nums[i];if ((preDiff >= 0 && curDiff < 0) || (preDiff <= 0 && curDiff > 0)){result++;preDiff = curDiff;}}return result;}
};53. 最大子数组和
题目描述:
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
解析:
贪心贪的是哪里呢?
如果 -2 1 在一起,计算起点的时候,一定是从1开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
局部最优的情况下,并记录最大的“连续和”,可以推出全局最优。
从代码角度上来讲:遍历nums,从头开始用count累积,如果count一旦加上nums[i]变为负数,那么就应该从nums[i+1]开始从0累积count了,因为已经变为负数的count,只会拖累总和。
这相当于是暴力解法中的不断调整最大子序和区间的起始位置。
那有同学问了,区间终止位置不用调整么? 如何才能得到最大“连续和”呢?
区间的终止位置,其实就是如果count取到最大值了,及时记录下来了。例如如下代码:
if (count > result) result = count;
这样相当于是用result记录最大子序和区间和(变相的算是调整了终止位置)。
代码实现:
class Solution {
public:int maxSubArray(vector<int>& nums) {if (nums.size() <= 1)return nums[0];int sum = 0;int result = INT32_MIN;for (int i = 0; i < nums.size(); i++){sum += nums[i];if (sum > result)result = sum;if (sum <= 0)sum = 0;}return result;}
};相关文章:

455. 分发饼干、376. 摆动序列、53. 最大子数组和
455.分发饼干 题目描述: 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块…...
基于Springbot+微信小程序的购药平台的设计与实现
基于Springbot微信小程序的购药平台的设计与实现 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、…...

aws lambda rust的sdk和自定义运行时
rust的aws sdk 参考资料 https://docs.aws.amazon.com/sdk-for-rust/latest/dg/getting-started.htmlhttps://awslabs.github.io/aws-sdk-rust/https://github.com/awslabs/aws-sdk-rusthttps://github.com/awsdocs/aws-doc-sdk-examples/tree/main/rust_dev_preview rus sd…...
[安装之3] 笔记本加装固态和内存条教程(超详细)
由于笔记本是几年前买的了,当时是4000,现在用起来感到卡顿,启动、运行速度特别慢,就决定换个固态硬盘,加个内存条,再给笔记本续命几年。先说一下加固态硬盘SSD的好处:1.启动快 2.读取延迟小 3.写…...

极客时间左耳听风-高效学习
左耳听风——高效学习篇 P95 | 高效学习:端正学习态度 本人真实⬇️⬇️⬇️⬇️ “ 大部分人都认为自己爱学习,但是: 他们都是只有意识没有行动,他们是动力不足的人。 他们都不知道自己该学什么,他们缺乏方向和目标。…...

MSR寄存器访问
1.介绍 MSR是CPU的一组64位寄存器,每个MSR都有它的地址值(如下图所示),可以分别通过RDMSR 和WRMSR 两条指令进行读和写的操作。 如图中为8个P-state寄存器,地址分别为0xC001 0064 ~ 0xC001 006B,每个寄存…...
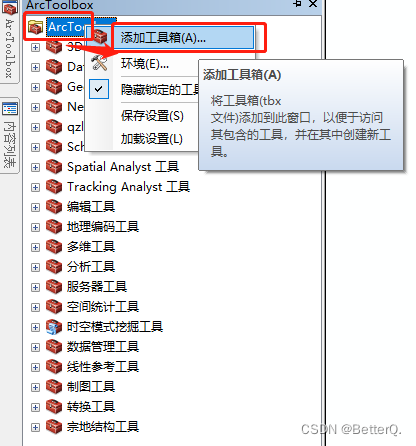
ArcGIS:模型构建器实现批量按掩膜提取影像
用研究区域的矢量数据来裁剪栅格数据集时,一般我们使用ArcGIS中的【按掩膜提取工具】。如果需要裁剪的栅格数据太多,处理起来非常的麻烦,虽然ArcGIS中有批处理的功能,但是还是需要手动选择输入输出数据。 如下图,鼠标…...

算法刷题打卡第94天: 找出给定方程的正整数解
找出给定方程的正整数解 难度:中等 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知,但它是单调…...
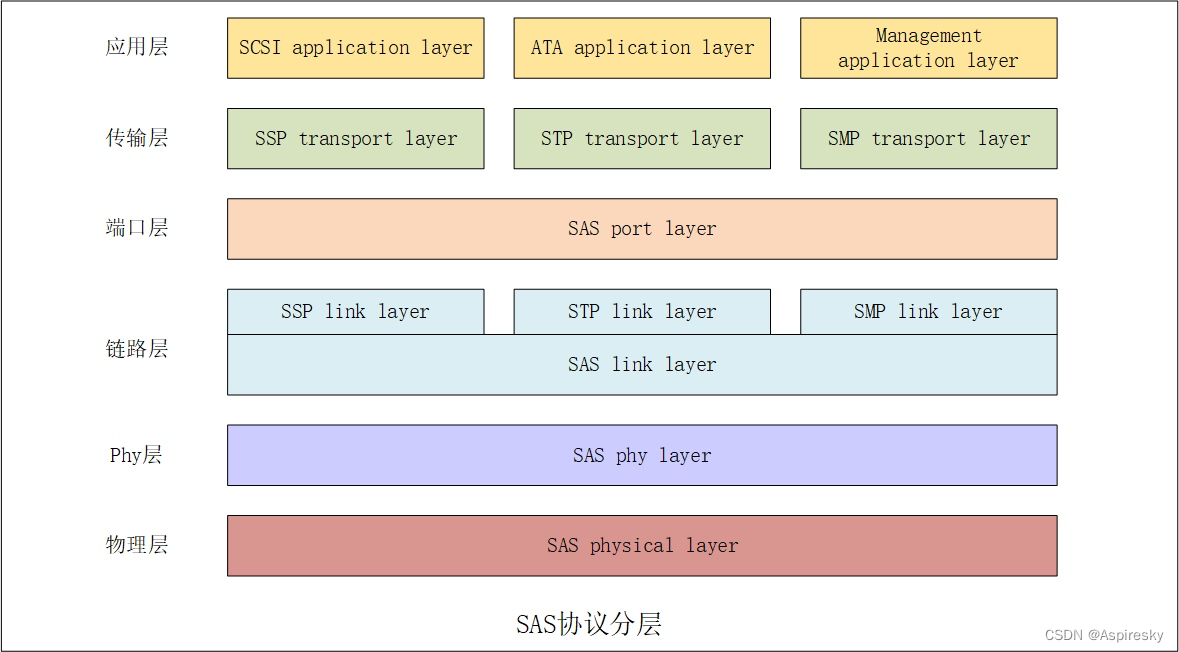
浅析SAS协议(1):基本介绍
文章目录概述SAS协议发展历程SAS技术特性SAS设备拓扑SAS phySAS地址SAS设备类型SAS协议分层参考链接概述 SAS,全称Serial Attached SCSI,即串行连结SCSI,是一种采用了串行总线的高速互连技术。通过物理上使用串行总线连结,在链路…...
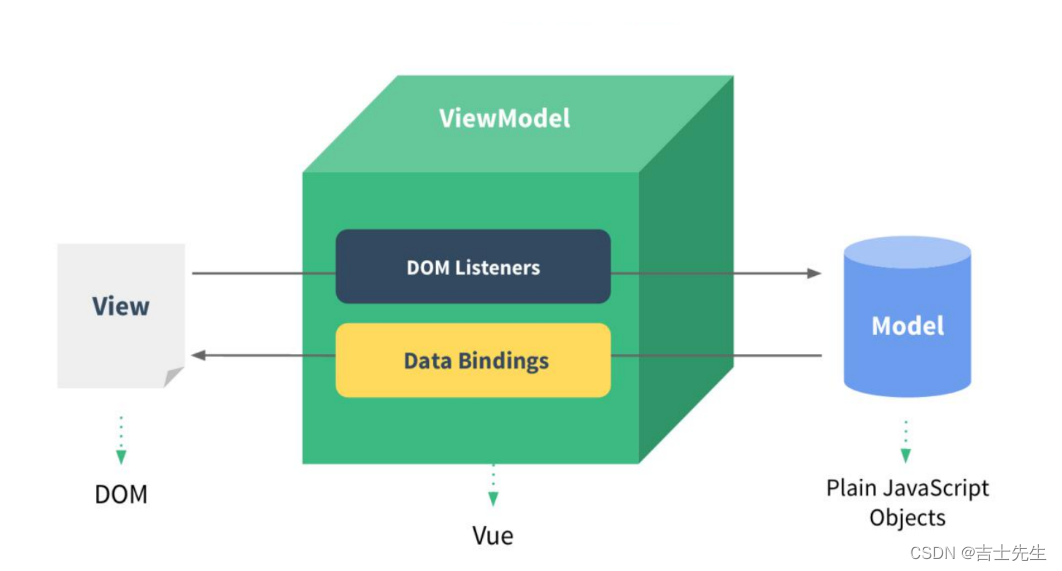
93.【Vue-细刷-02】
Vue-02(十六)、基本列表渲染 (v-for)1.使用v-for遍历数组2.使用v-for遍历对象3.使用v-for遍历字符串(十七)、列表过滤 (filter())1.⭐JS中Change属性的原生状态⭐2.使用watch监听实现3.const {xxx} this 在Vue的作用⭐⭐4.JS箭头函数参数的简写⭐5.使用computed进行计算实现(最…...
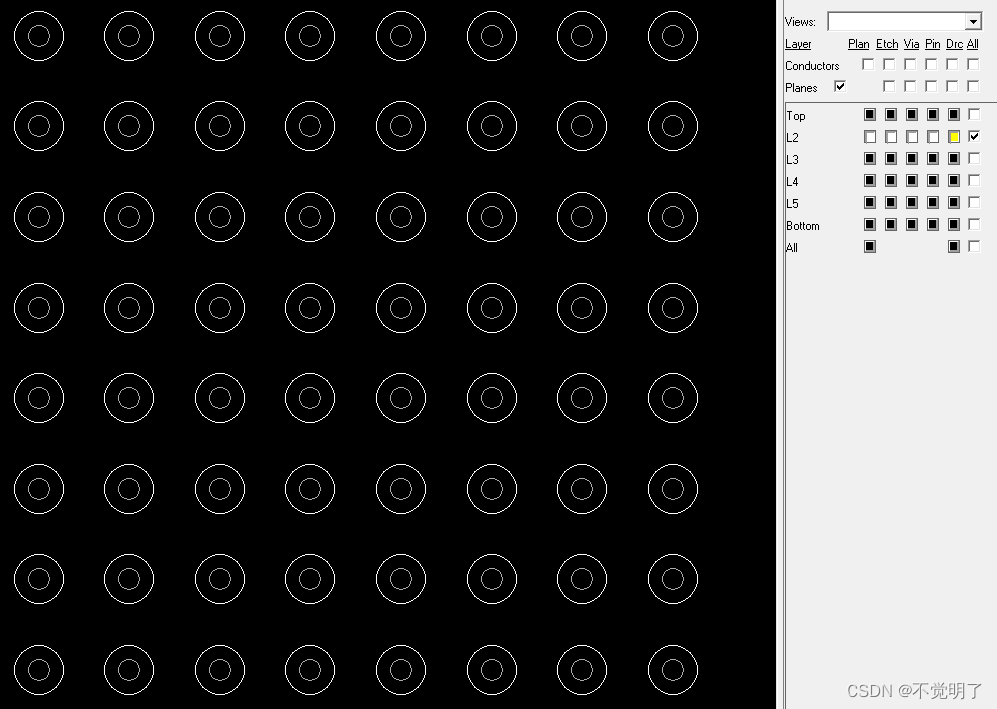
Allegro负片层不显示反盘的原因和解决办法
Allegro负片层不显示反盘的原因和解决办法 在用Allegro做PCB设计的时候,负片设计是较为常用的一种方式,有时会出现打开负片层却看不到反盘的情况,如下图 L2层是负片层 L2层仍然只能看到盘 如何才能看到反盘显示的效果,具体操作如下 首先确定L2层层叠里面设置的是负片...
ACM数论 裴蜀定理(贝祖定理)
一.内容定义 「裴蜀定理」,又称贝祖定理(Bzouts lemma)。是一个关于最大公约数的定理。其内容定义为:对于不全为零的任意整数 a 和 b,记二者的最大公约数为 g 即 gcd(a,b) g,则对于任意整数 x 和 y 都一定…...
解析)
基础篇—CSS Position(定位)解析
CSS Position(定位) position 属性指定了元素的定位类型。 position 属性的五个值: relativefixedabsolutesticky元素可以使用的顶部,底部,左侧和右侧属性定位。然而,这些属性无法工作,除非是先设定position属性。他们也有不同的工作方式,这取决于定位方法。 1、static…...

正则表达式与grep
基本正则表达式BRE集合 匹配字符匹配次数位置锚定 符号作用^尖角号,用于模式的最正常,如“^haha”,匹配以haha单词开头的行$美元符,用于模式的最右侧,如“haha$”,表示haha单词结尾的行^$组合符ÿ…...
开发必备的IDEA 插件!效率提升 50 倍!
日常开发中,面向百度编程的程序员,很多时候,你跟大佬级别的差距,可能不仅仅是知识面的差距,还有就是开发效率的差距。以下是我常用的几个IDEA插件,废话不多说,直接肝干货! 1. Codot…...

aws eks 集群访问ecr仓库拉取镜像的认证逻辑
本文主要讨论三个问题 ecr帮助程序在docker上如何配置eks集群访问ecr仓库的逻辑kubelet授权ecr的源码分析 ecr帮助程序 在docker环境下,可以通过在$HOME/.docker/config.json中指定凭证管理程序 docker login aws同样提供了证书助手,避免手动执行ecr认…...
Linux Socket Buffer介绍
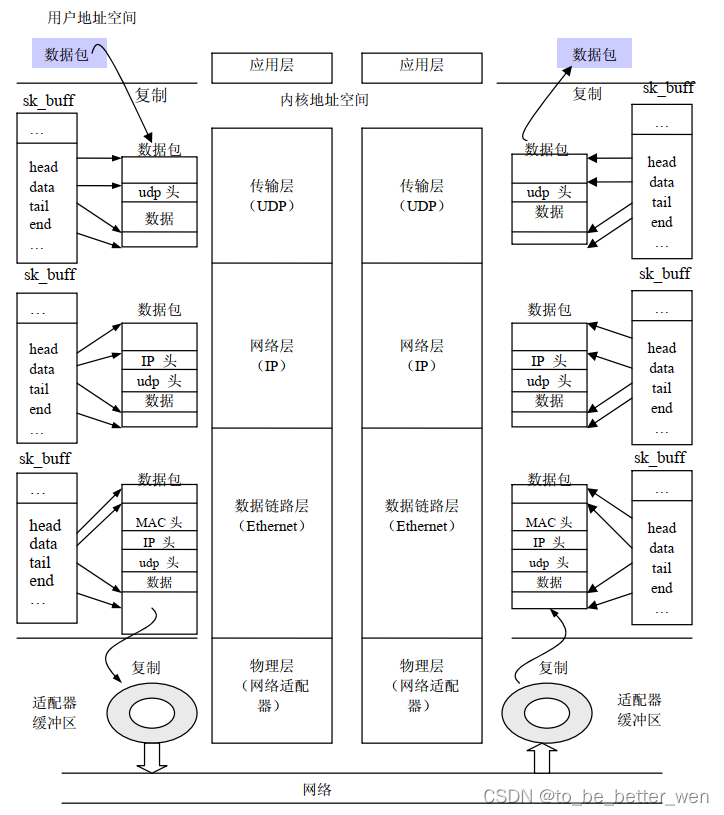
一. 前言 Linux内核网络子系统的实现之所以灵活高效,主要是在于管理网络数据包的缓冲器-socket buffer设计得高效合理。在Linux网络子系统中,socket buffer是一个关键的数据结构,它代表一个数据包在内核中处理的整个生命周期。 二. Socket Bu…...
ACL与NAT
ACL---访问控制列表,是一种策略控制工具 功能:1.定义感兴趣流量(数据层面 ) 2.定义感兴趣路由(控制层面) ACL 条目表项组成: 编号规则:步数或者跳数默认值为5,…...

使用gdb来debug程序并查找Segmentation fault原因
GDB 调试前言GDB基础用法1.启动及退出调试2.设置参数3.执行程序4.流程控制5.设置断点6.输出信息7.查看栈帧8.info命令9.显示源码GDB调试coredump文件关注公众号【程序员DeRozan】,回复【1207】,免费获取计算机经典资料及现金红包 前言 在开发程序时&…...

vbs简单语法及简单案例
文章目录一、简单语法1、变量2、输入3、输出4、选择语句5、循环二、用记事本编译中文乱码问题三、制作一个简单vbs脚本表白一、简单语法 1、变量 语法: dim 变量名例: dim a,b a1 b2 msgbox ab运行: 2、输入 语法:InputBox(…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
