各种查找算法的效率分析
各种查找算法的效率
- 顺序查找
- 一般顺序表(没有顺序,随机排列)
- 成功时平均查找长度: 1 + . . . + n n = n + 1 2 \frac{1+...+n}{n}=\frac{n+1}{2} n1+...+n=2n+1
- 失败时平均查找长度: n n n
- 有序顺序表(按照递增或递减排列)

- 成功时平均查找长度: 1 + . . . + n n = n + 1 2 \frac{1+...+n}{n}=\frac{n+1}{2} n1+...+n=2n+1
- 失败时平均查找长度: 1 + 2 + . . . + n + n n + 1 = n 2 + n n + 1 \frac{1+2+...+n+n}{n+1}=\frac{n}{2}+\frac{n}{n+1} n+11+2+...+n+n=2n+n+1n
- 一般顺序表(没有顺序,随机排列)
- 折半查找(二分查找)
- 用折半查找法找到给定值的比较次数不会超过树的高度(n个元素的树高为 ⌈ l o g 2 ( n + 1 ) ⌉ \lceil log_2(n+1)\rceil ⌈log2(n+1)⌉)
- 成功时的平均查找长度: A S L = 1 n ( 1 × 1 + 2 × 2 + 3 × 4 + . . . + h × 2 h − 1 = n + 1 n l o g 2 ( n + 1 ) − 1 ≈ l o g 2 ( n + 1 ) − 1 ASL=\frac{1}{n}(1\times 1+2\times 2+3\times 4+...+h\times 2^{h-1}=\frac{n+1}{n}log_2(n+1)-1\approx log_2(n+1)-1 ASL=n1(1×1+2×2+3×4+...+h×2h−1=nn+1log2(n+1)−1≈log2(n+1)−1
- 折半查找的时间复杂度为 O ( l o g 2 n ) O(log_2n) O(log2n)
- 分块查找(索引顺序查找)
- 平均查找长度: A S L = L I + L S ASL=L_I+L_S ASL=LI+LS( L I L_I LI为索引查找的平均查找长度, L S L_S LS为块内查找的平均查找长度)
- 如将长度为n的查找表均匀地分成b块,每块有s个记录,在等概率情况下,若在块内和索引表中均采用顺序查找,则平均查找长度为 A S L = L I + L S = b + 1 2 + s + 1 2 = s 2 + 2 s + n 2 s ASL=L_I+L_S=\frac{b+1}{2}+\frac{s+1}{2}=\frac{s^2+2s+n}{2s} ASL=LI+LS=2b+1+2s+1=2ss2+2s+n。可见若 s = n s=\sqrt{n} s=n,则平均查找长度取最小值 n + 1 \sqrt{n}+1 n+1
- 平均查找长度: A S L = L I + L S ASL=L_I+L_S ASL=LI+LS( L I L_I LI为索引查找的平均查找长度, L S L_S LS为块内查找的平均查找长度)
- 树型查找
- 二叉排序树(主要取决于树的高度)
- 若二叉排序树的左右子树高度之差不超过1(即平衡二叉树),则平均查找长度为 O ( l o g 2 n ) O(log_2{n}) O(log2n)
- 若二叉排序树是一个只有左(右)孩子的单支树,则平均查找长度为 O ( n ) O(n) O(n)
- 平衡二叉树(查找过程与二叉排序树相同)
- 平均查找长度为 O ( l o g 2 n ) O(log_2n) O(log2n)
- 因为含有n个节点的平衡二叉树的最大深度为 O ( l o g 2 n ) O(log_2n) O(log2n)
- 平均查找长度为 O ( l o g 2 n ) O(log_2n) O(log2n)
- 红黑树
- 平均查找长度为 O ( l o g 2 n ) O(log_2n) O(log2n)
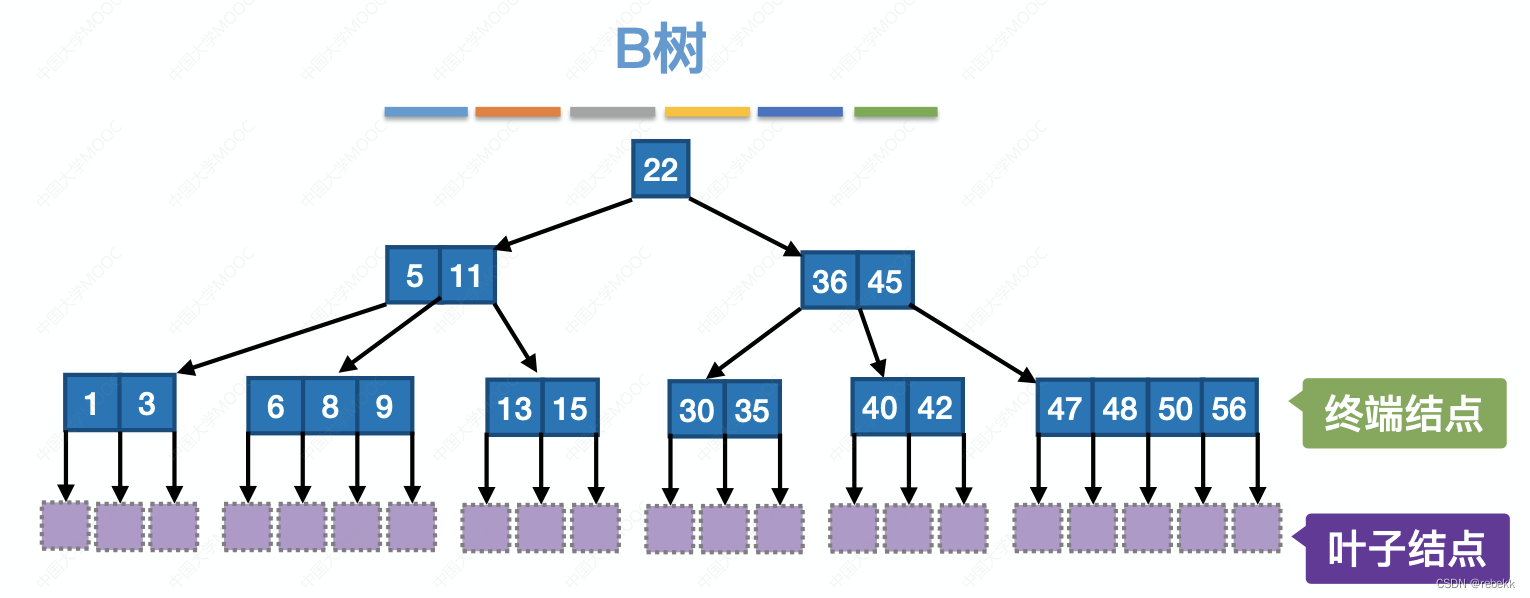
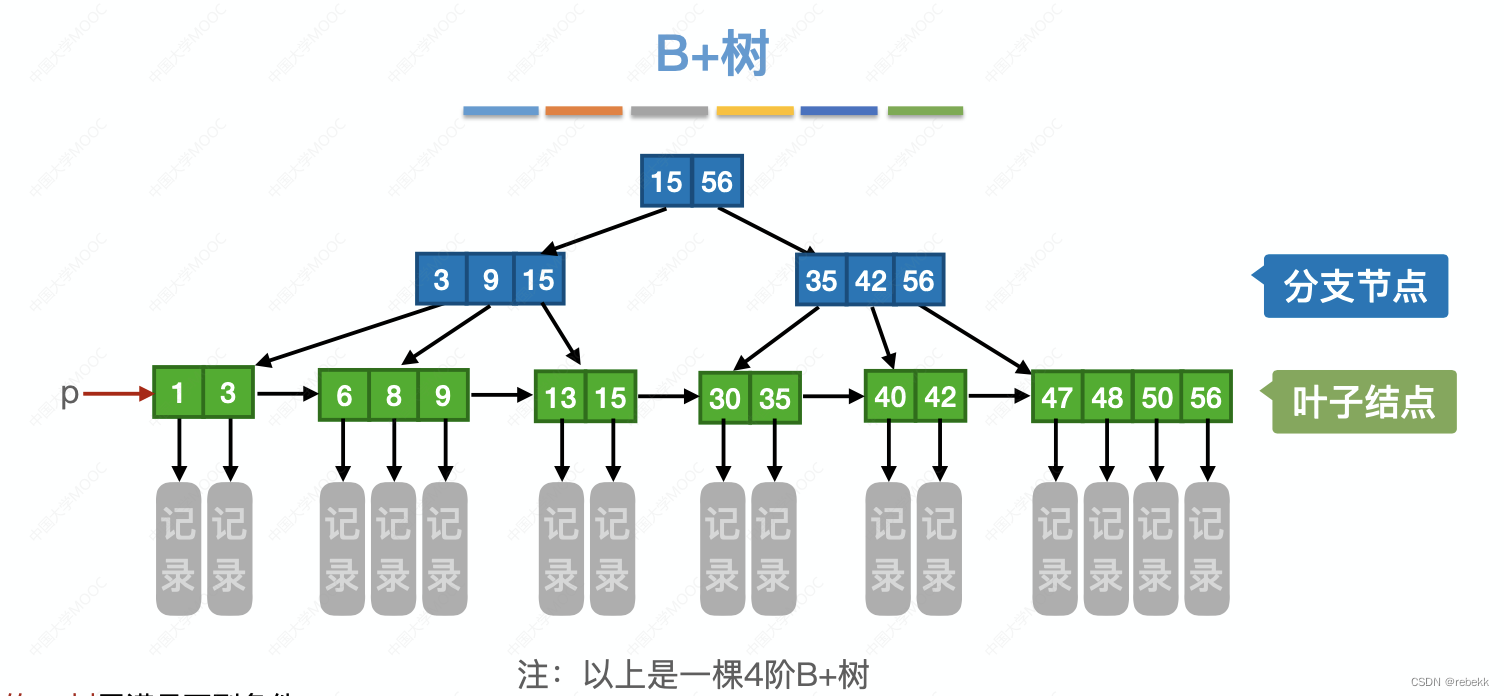
- B树和B+树
- 二叉排序树(主要取决于树的高度)
- 散列表
虽然散列表在关键字与记录的存储位置之间建立了直接映像,但由于冲突的产生,使得散列表的查找过程仍然是一个给定值和关键字进行比较的过程。因此仍需以平均查找长度作为衡量散列表的查找效率的度量。
散列表的查找效率取决于三个因素:散列函数、冲突处理的方法和装填因子。
直观的看, α \alpha α越大,表示装填的记录越满,发生冲突的可能性越大。
折半查找(二分查找)与二叉排序树的区别
二叉排序树与二分查找(折半查找)的查找过程相似,平均时间性能差不多。不同点如下:
- 唯一性:二分查找的判定树唯一,而二叉排序树随着关键字插入顺序不同可能生成不同的二叉排序树
- 插入和删除:二分查找的对象是有序顺序表,若有插入和删除节点的操作,所花的代价是 O ( n ) O(n) O(n);二叉排序树则无需移动节点,只需修改指针即可完成插入和删除操作
- 适用于动态还是静态:当有序表是静态查找表时,宜用顺序表作为其存储结构,采用二分查找实现找操作;若有序表是动态查找表,应选择二叉排序树作为其逻辑结构
平衡二叉树和红黑树的区别
二者的查、插、删的时间复杂度都是 O ( l o g 2 n ) O(log_2n) O(log2n),区别如下:
- 平衡二叉树的插入和删除很容易破坏平衡特性,故插/删后大都需要调整树的形态(计算平衡因子+找到最小不平衡树+LL/RR/LR/RL),这样一来时间开销就很大;而红黑树由于其特性,很多时候插入删除后并不会破坏红黑特性,即便需要调整一般也都可以在常数级时间内完成
- 即虽然二者的插、删、查的时间复杂度都是 O ( l o g 2 n ) O(log_2n) O(log2n),但实际上红黑树的插入和删除性能更好一点,平衡二叉树的查找性能更好一点
- 使用场景:平衡二叉树适用于以查为主、很少插入/删除的场景;红黑树适用于频繁插入、删除的场景,实用性更强
B树和B+树的区别
二者相同点是:除根节点外,最少 ⌈ m 2 ⌉ \lceil\frac{m}{2}\rceil ⌈2m⌉个分叉(确保节点不要太空)。任何一个节点的子树都要一样高(确保绝对平衡)
| - | m阶B树 | m阶B+树 |
|---|---|---|
| 类比 | 二叉查找树的进化 --> m叉查找树 | 分块查找的进化 --> 多级分块查找 |
| 关键字与分叉 | n个关键字对应n+1个分叉(子树) | n个关键字对应n个分叉 |
| 节点包含的信息 | 所有节点中都包含记录的信息 | 只有最下层叶子节点才包含记录的信息(每个节点能存的信息更多,因此可以使树更矮),且叶节点包含所有的关键字 |
| 查找方式 | 不支持顺序查找。查找成功时,可能停在任何一层节点,查找速度不稳定 | 支持顺序查找。查找成功或失败都会到达最下一层节点,查找速度稳定 |
相关文章:

各种查找算法的效率分析
各种查找算法的效率 顺序查找 一般顺序表(没有顺序,随机排列) 成功时平均查找长度: 1 . . . n n n 1 2 \frac{1...n}{n}\frac{n1}{2} n1...n2n1失败时平均查找长度: n n n 有序顺序表(按照递增或递…...

微报告下载!市场不确定性周期下的激光雷达前装赛道
随着理想L9 Pro版本(取消激光雷达)的上市(相比AD Max版本降价3万元),中国乘用车市场仅剩下蔚来(NT2.0平台)、阿维塔11仍全系标配激光雷达。 这对于激光雷达赛道来说,是一个明确的信…...
Java版企业电子招标采购系统源码Spring Cloud + Spring Boot +二次开发+ MybatisPlus + Redis tbms
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查…...
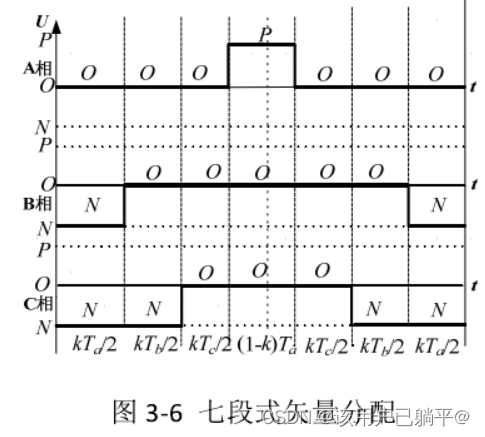
并网逆变器学习笔记6---三电平SVPWM下的连续和不连续调制
之前在学习中总结过一次DPWM策略选择:并网逆变器学习笔记5---三电平DPWM 但是对于三电平逆变器而言,如何从连续调制切换到不连续调制,存在一些疑惑点,下午闲来无事,把SVPWM下的连续调制和不连续调制的开关状态选择&am…...
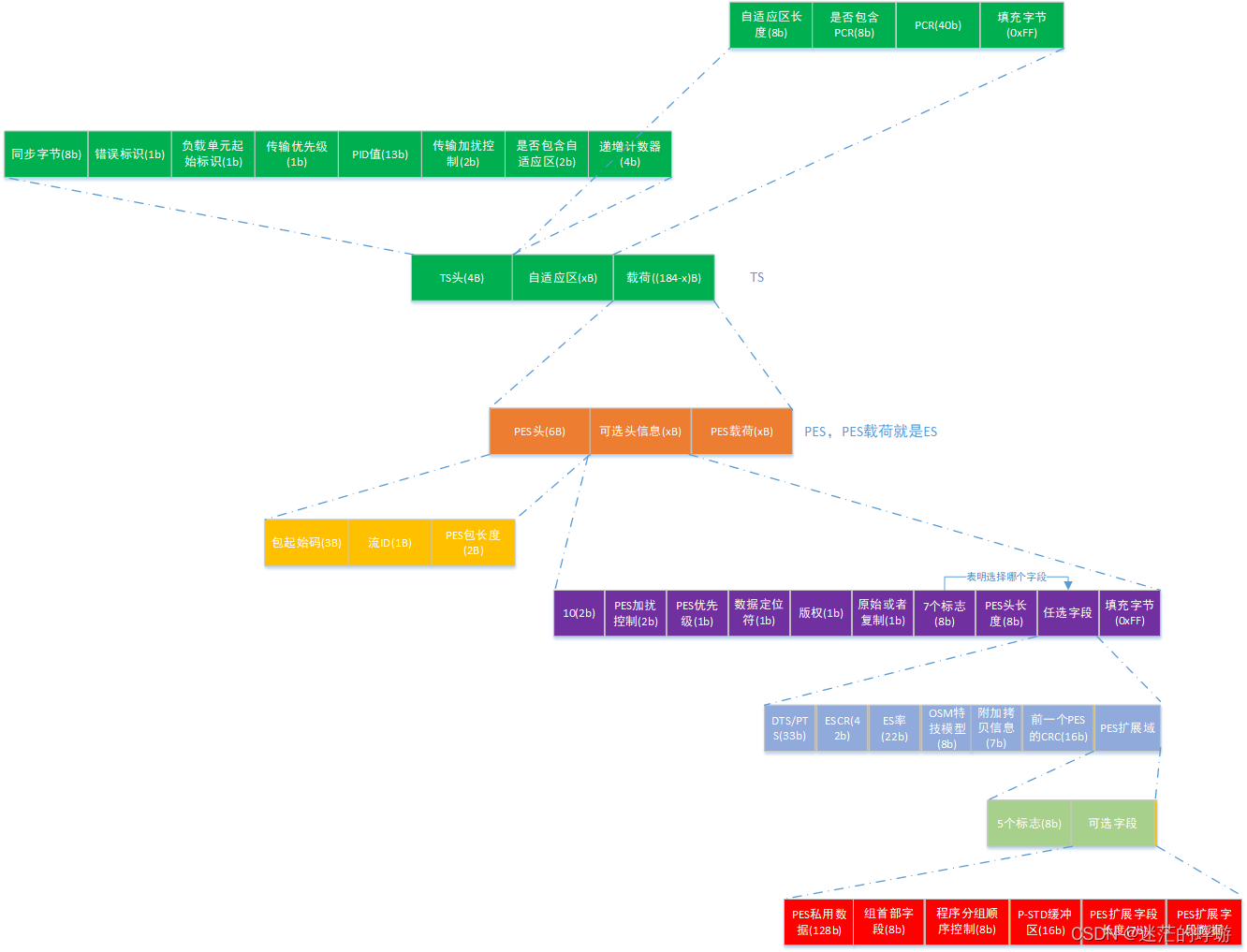
TS协议之PES(ES数据包)
TS协议之PAT(节目关联表)TS协议之PMT(节目映射表)TS协议之PES(ES数据包) 该文档已上传:下载地址 1. 概要 1.1 TS数据包(PES)协议数据组成 TSTS头PES头ES。TS…...

银河麒麟V10 SP3 X86 二进制文件部署 mysql-5.7.29 GTID 半同步复制的双主架构
文章目录 [toc]啰嗦一下mysql 的 AB 复制和 gtid 复制的优缺点AB 复制(Asynchronous Replication)GTID 复制(Global Transaction Identifier Replication) mysql gtid 并行复制和半同步复制的优缺点并行复制(Parallel …...

python爬虫3:requests库-案例1
python爬虫3:requests库-案例1 前言 python实现网络爬虫非常简单,只需要掌握一定的基础知识和一定的库使用技巧即可。本系列目标旨在梳理相关知识点,方便以后复习。 申明 本系列所涉及的代码仅用于个人研究与讨论,并不会对网…...

面部表情识别(Pytorch):人脸检测模型+面部表情识别分类模型
目录 0 相关资料1 基于人脸检测面部表情分类识别方法2 项目安装2.1 平台与镜像2.2 项目下载2.3 模型下载2.4 上传待测试图片2.5 项目安装 3 demo测试 0 相关资料 面部表情识别2:Pytorch实现表情识别(含表情识别数据集和训练代码):https://blog.csdn.net…...
外卖点餐小程序开源源码——支持扫码点餐
一套支持店内扫码点餐、外卖点餐配送于一体的餐饮系统,支持商家创建优惠券,支持商家自定义打印机功能,支持商家财务管理,支持商户菜品管理,支持菜品自定义分类,支持商家招募骑手入驻功能。系统基于thinkphp…...
十分钟掌握使用 SolidJS 构建全栈 CRUD 应用程序
我们可以开始讨论 SolidJS,说它比React更好,但没有必要做这种比较。SolidJS只是众多前端框架之一,旨在在Web上快速创建数据驱动。那么,我们为什么要突出这个新孩子呢? 首先,我们不能忽视SolidJS不使用虚拟…...

LabVIEW开发多材料摩擦电测量控制系统
LabVIEW开发多材料摩擦电测量控制系统 摩擦电效应是两个物体摩擦在一起,电荷从一个物体转移到另一个物体的现象,从而导致两个物体携带相等和相反的电荷。接触和充电是主导该过程的两个关键因素。当静电荷累积到一定水平时,可能会出现放电现象…...
【Linux】网络基础1
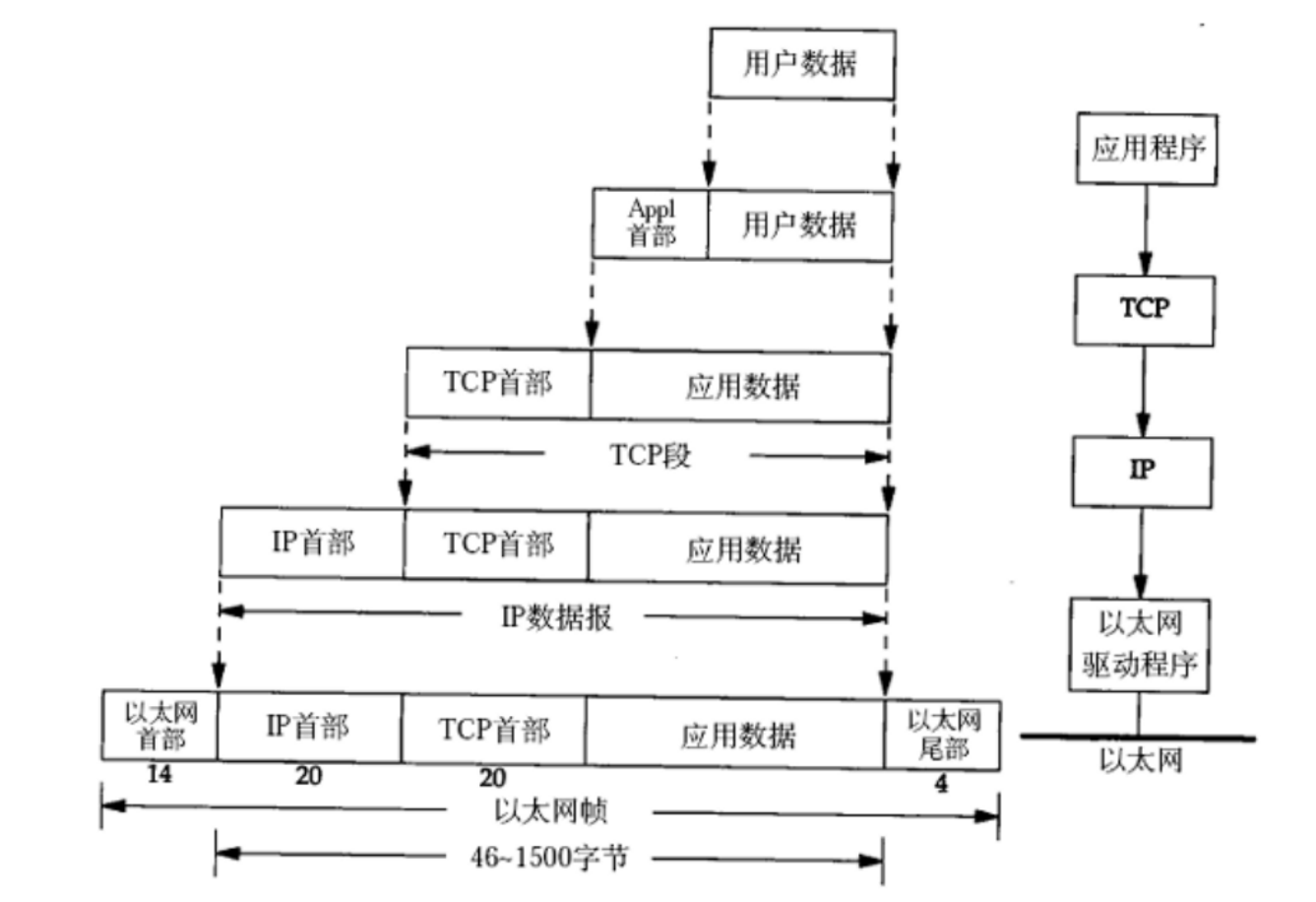
文章目录 网络基础11. 计算机网络背景1.1 网络发展 2. 认识协议2.1 网络协议2.2 OSI七层模型2.3 TCP/IP五层(或四层)模型 3. 网络传输基本流程3. 1 数据报封装和分用 4. 网络中的地址管理4.1 认识IP地址 5. 认识MAC地址 网络基础1 1. 计算机网络背景 1…...

HTML - Javascript - 原生的JS HTTP请求:实用主义的一篇文章
HTML - Javascript - 原生的JS HTTP请求:实用主义的一篇文章 前言 虽然现在使用JQuery等可以做到很方便的HTTP请求,但是这样做毕竟要引入一些JS文件。 如果想使用原生的JS进行HTTP网络请求应该怎样呢?可以使用XMLHttpRequest。 使用方法 …...
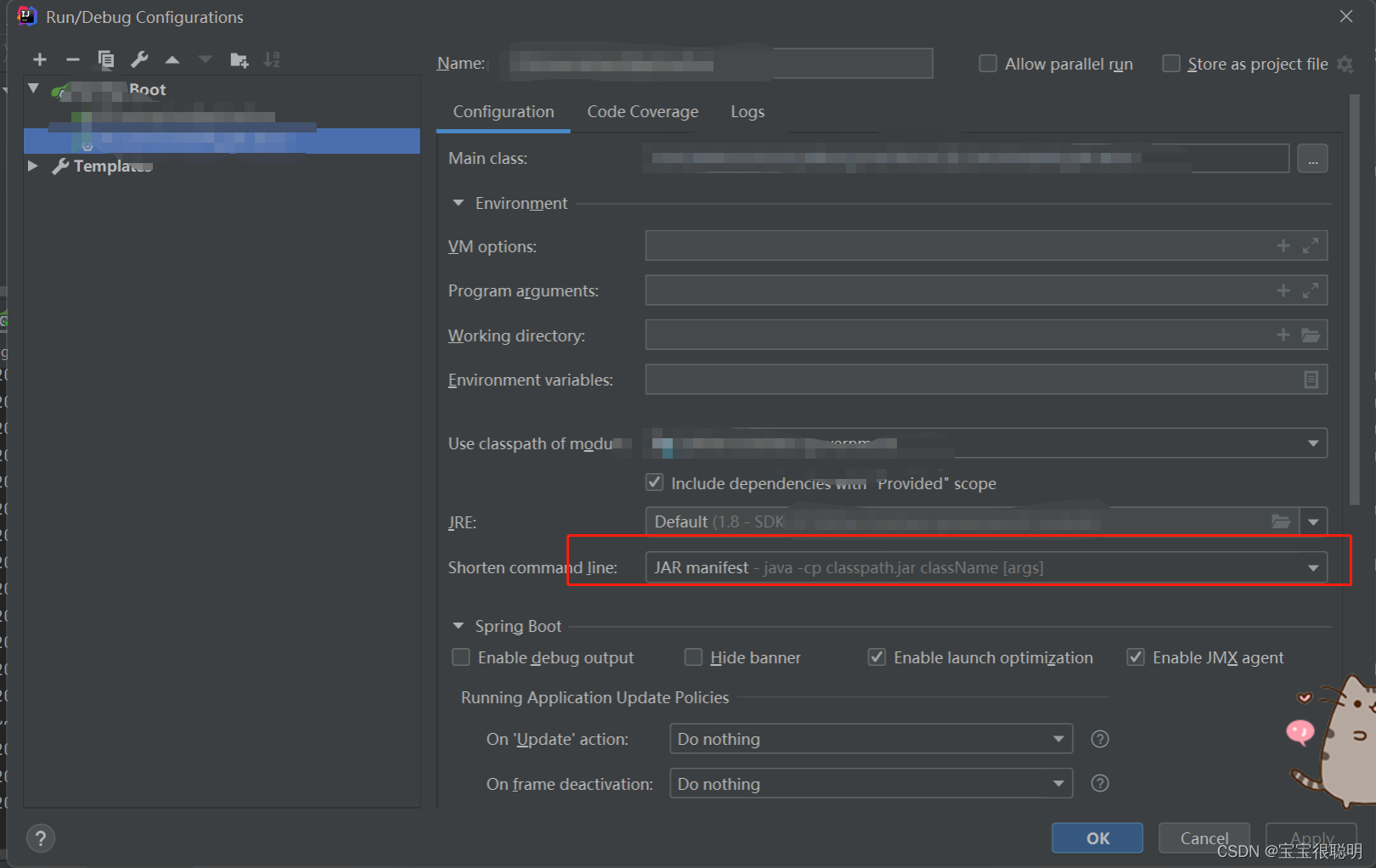
Intellij IDEA运行报Command line is too long的解决办法
想哭,vue前端运行起来,对应的后端也得起服务。 后端出的这个bug,下面的博客写的第二种方法,完整截图是下面这个。 Intellij IDEA运行报Command line is too long的解决办法 - 知乎 (zh…...

信号槽传输过程中指针所指对象的生命周期
在子线程中的一个槽函数,当读取到dxf文件完成后,结果通过在该槽函数中的 dx_data* pDxfData 指针变量读取。 然后通过QVariant封装该指针变量。发送到主线程中。 void qcWorker::slotReadDxfFile(QString dir) {bool bRtn{ false }; //定义一个局部指针…...

c++ 递归锁的使用
非递归锁 同一个线程里,在锁未释放的情况下反复加锁,会导致死锁。 示例 #include <iostream> #include <mutex> #include <thread> #include <unistd.h> using namespace std;std::mutex m_mutex;void Func() {m_mutex.lock(…...

Oracle TDE wallet
1. 钱夹密码千万不能忘记,这也是使用TDE 需要承担的风险。 2. 只要将wallet cwallet.sso 拷贝过去,加密没有意义! 钱夹的备份 正如上述,已经加密过的表列或者表空间,钱夹必须打开才能够查询到里面的数据。如果钱夹丢…...

多模态学习
一、目标 三、多模态核心任务 题目:...
Android学习之路(2) 文本设置
Android学习之路(1) 文本 一、设置文本内容 设置文本内容的两种方式: 一种是在XML文件中通过属性android:text设置文本代码如下 <TextViewandroid:id"id/tv_hello"android:layout_width"wrap_content"android:layout_height"wrap_c…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...