用C语言实现定积分计算(包括无穷积分/可自定义精度)
关于严谨性的声明:
在用C语言进行定积分的计算之前,我需要声明以下几点:
一、我们所进行定积分计算的函数都是应当是黎曼可积的,这保证了我们即使均匀地分割区间也保证了积分的收敛性。
二、我们同时还应该认识到,鉴于某些函数不一定是在每一点上都是可导的,因此我们将不使用所谓的利用到导数来提高计算精度的这种算法。
三、考虑到某些函数并不是连续的,如果涉及到这些计算,那么我们计算到的结果将会是一个瑕积分,如果这个瑕积分是收敛的,那么我们得到的就是收敛值。如果不收敛,这个瑕积分的值并不是积分主值,因为我们没有办法保证瑕点附近的两个点的趋近于瑕点的趋势是一样的。
四、如果你计算的是一个无穷积分,如果这个无穷积分是收敛的,那么我们得到的就是收敛值。如果不收敛,那么我们得到的值将会是它的积分主值。
另外,考虑到C语言精度的限制,我们无需写一个专门的程序用来计算瑕积分,因为当我们用C语言计算这个瑕积分的时候,就相当于我们采用了两边趋近瑕点取极限的办法来计算瑕积分,当然了,由于我们采用了均匀分割的方法,所以当我们两边趋近的时候并不能使得其以任意方式趋近瑕点。除此之外,你应当保证瑕点不在积分区间的边界上。对于无穷积分,不论我们怎么切割区间都不能使得划分的区间足够小,除非我们划分区间的时候将他划为了无穷份,当然了这个划分的份数应当是无穷积分区间大小的高阶无穷大。事实上,这是做不到的,因此我们将采用函数变换的方法将无穷积分转化为有限积分。
最后,鉴于C语言的精度限制,如果我们只是计算性质较为良好的函数,那么我们将会获得非常好的精度,甚至是仅仅只是可测的函数,也是可以计算的。但如果我们计算的是有着许多无穷间断点,或有着许多瑕点的函数,或者是震荡很厉害的函数,那么它的积分值误差将会较大。最后我还想声明一点,那就是我们不应该用该程序去计算本身就是发散的积分因为你甚至可能得到的仅仅只是个有限值。
1. 有限积分
根据我们在之前所说的,我们可以轻易得到:
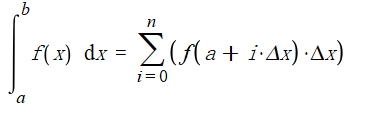
其中:
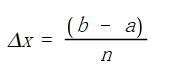
因此,我们不难写出以下代码:
//定义一个C语言函数,用于进行微积分的数值运算
long double integrate(long double a, long double b, long int n)
{long double s = 0;long double dx = (b - a) / n;for (long int i = 1; i < n; i++){s += f(a + i * dx) * dx;}return s;
}其中函数 long double integrate(long double a, long double b, long int n) 就是用来计算定积分的函数。值得注意的是,在调用该函数之前,我们应当提前定义被积函数f(x)。其中a,b,n分别为积分下限,积分上限和区间分割数。
以上是矩形法,数值计算的精度并不是非常高,我们改进一下,使用梯形法,得到:
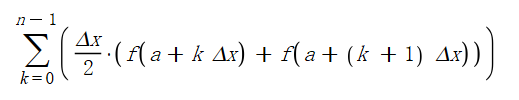
其中:
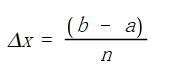
因此,我们不难写出以下代码:
long double integral(long double x0, long double xt, long long n)
{long double sum = 0;long double dx = (xt - x0) / n;for (long long k = 0; k < n; k++){sum += ((f(x0 + k * dx) + f(x0 + (k + 1) * dx)) / 2) * dx;}return sum;
}相较于矩形法,梯形法不论是精度还是速度都有着不小的提升。
2. 无穷积分
我们已经讨论过无穷积分采用直接计算的困难的地方,因此我们将采用函数变换的方法。
我们很容易注意到:
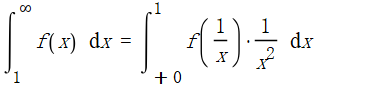
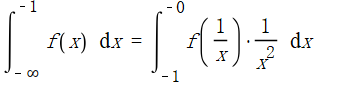
这两个式子是等价的,因此我们可以将所有的无穷积分转化为无限积分。只需要利用积分区间的可叠加性即可。因此不多叙述。
有了相关的理论铺垫后,我们添加一点点细节。以下直接给出关于定积分的计算代码:(详细信息在注释里)
#include <stdio.h>
#include <math.h> #define inf INFINITY// 定义用于被积分的函数
long double f(long double x)
{return exp(x);
}// 定义被积函数的特殊形式用于计算无穷积分
long double g(long double x)
{long double y = 1.0 / x;long double result = f(y) * (1.0 / (x * x));return result;
}// 一个用于计算定积分的C语言子程序
//值得注意的是我们还将数学函数作为参数传给了这个函数,这可以让我们有多个数学函数时,可以指定数学函数计算
long double integral(long double x0, long double xt, long long n, long double (*f)(long double))
{//对于黎曼可积的函数,这样的积分值为零,直接返回。if ((x0 == xt)&&((x0 != INFINITY && x0 != -INFINITY)&&(xt != INFINITY && xt != -INFINITY)))return 0;else{long double sum = 0;long double dx = (xt - x0) / n; for (long long k = 0; k < n; k++){sum += ((f(x0 + k * dx) + f(x0 + (k + 1) * dx)) / 2) * dx;}return sum;}
}// 定义绝对值函数
static long double lfabs(long double x)
{if (x >= 0)return x;elsereturn -x;
}//用于计算指定精度的定积分的函数
//值得注意的是我们还将数学函数作为参数传给了这个函数,这可以让我们有多个数学函数时,可以指定数学函数计算
long double definite_integral(long double x0, long double xt, long double esp, long double (*f)(long double))
{//如果积分限不是无穷则进行经典数值积分计算if ((x0 != INFINITY && x0 != -INFINITY) && (xt != INFINITY && xt != -INFINITY)) {long long i = 10; long double d = 0;long double s = 0;do {long double s1 = integral(x0, xt, i, f);long double s2 = integral(x0, xt, 10 * i, f);i *= 10;s = s2;d = lfabs(s1 - s2);} while (d > esp);return s;}//如果是无穷积分,则采用特殊方法进行数值计算else {//积分下限有限大小//值得注意的是,当我们使用g函数进行积分的时候,有一个积分限迎丹是0,然而事实上我们以一个很小的小数来替代if (x0 != INFINITY && x0 != -INFINITY){if (xt == INFINITY){long double s1 = definite_integral(x0, 1, esp, f);long double s2 = definite_integral(esp/1000000.0, 1, esp, g);return (s1 + s2);}else if (xt == -INFINITY){long double s1 = definite_integral(-1, x0, esp, f);long double s2 = definite_integral(-1, -esp/1000000.0, esp, g);return -(s1 + s2);}}//积分上限有限大小else if (xt != INFINITY && xt != -INFINITY){if (x0 == INFINITY){long double s1 = definite_integral(xt, 1, esp, f);long double s2 = definite_integral(esp/1000000.0, 1, esp, g);return -(s1 + s2);}else if (x0 == -INFINITY){long double s1 = definite_integral(-1, xt, esp, f);long double s2 = definite_integral(-1, -esp/1000000.0, esp, g);return (s1 + s2);}}//积分上下限都为无穷else if (x0 == -INFINITY && xt == INFINITY){long double s1 = definite_integral(-1, 1, esp, f);long double s2 = definite_integral(-1, -esp/1000000.0, esp, g);long double s3 = definite_integral(esp/1000000.0, 1, esp, g);return (s1 + s2 + s3);}else if (x0 == INFINITY && xt == -INFINITY){long double s1 = definite_integral(-1, 1, esp, f);long double s2 = definite_integral(-1, -esp/1000000.0, esp, g);long double s3 = definite_integral(esp/1000000.0, 1, esp, g);return -(s1 + s2 + s3);}//如果积分是从正无穷积分到正无穷或从负无穷积分到负无穷则需要另外判断else{if (x0 == INFINITY && xt == INFINITY){if (f(INFINITY) == 0)return 0;elsereturn NAN;}else if (x0 == -INFINITY && xt == -INFINITY){if (f(-INFINITY) == 0)return 0;elsereturn NAN;}}return NAN;}
}int main()
{long double x0, xt, esp;printf("如果要输入无穷大或无穷小,请输入inf或-inf\n");printf("请输入积分区域(x0,xt),和最大容忍误差esp:>>");scanf("%lf %lf %lf", &x0, &xt, &esp);long double result = definite_integral(x0, xt, esp, &f);printf("%.16lf\n", result);return 0;
}在计算指定定积分精度的C函数中,对于无穷积分我们通过转化为有限积分后再调用自身的方式有效地减伤了大量大代码量。这也是为什么要把我们定义的数学函数作为参数传给函数的原因。
如下:
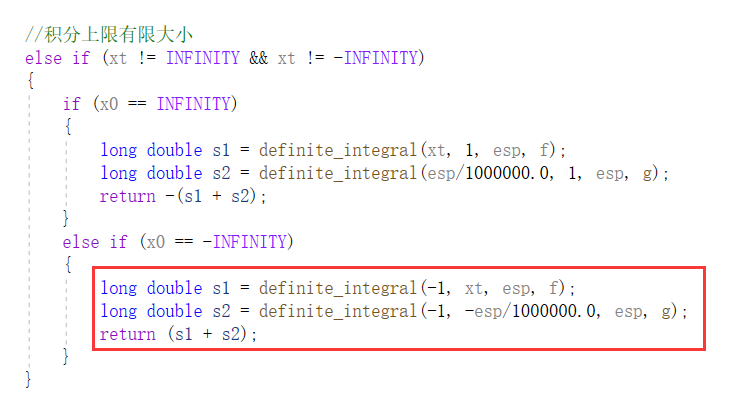
代码的运行:
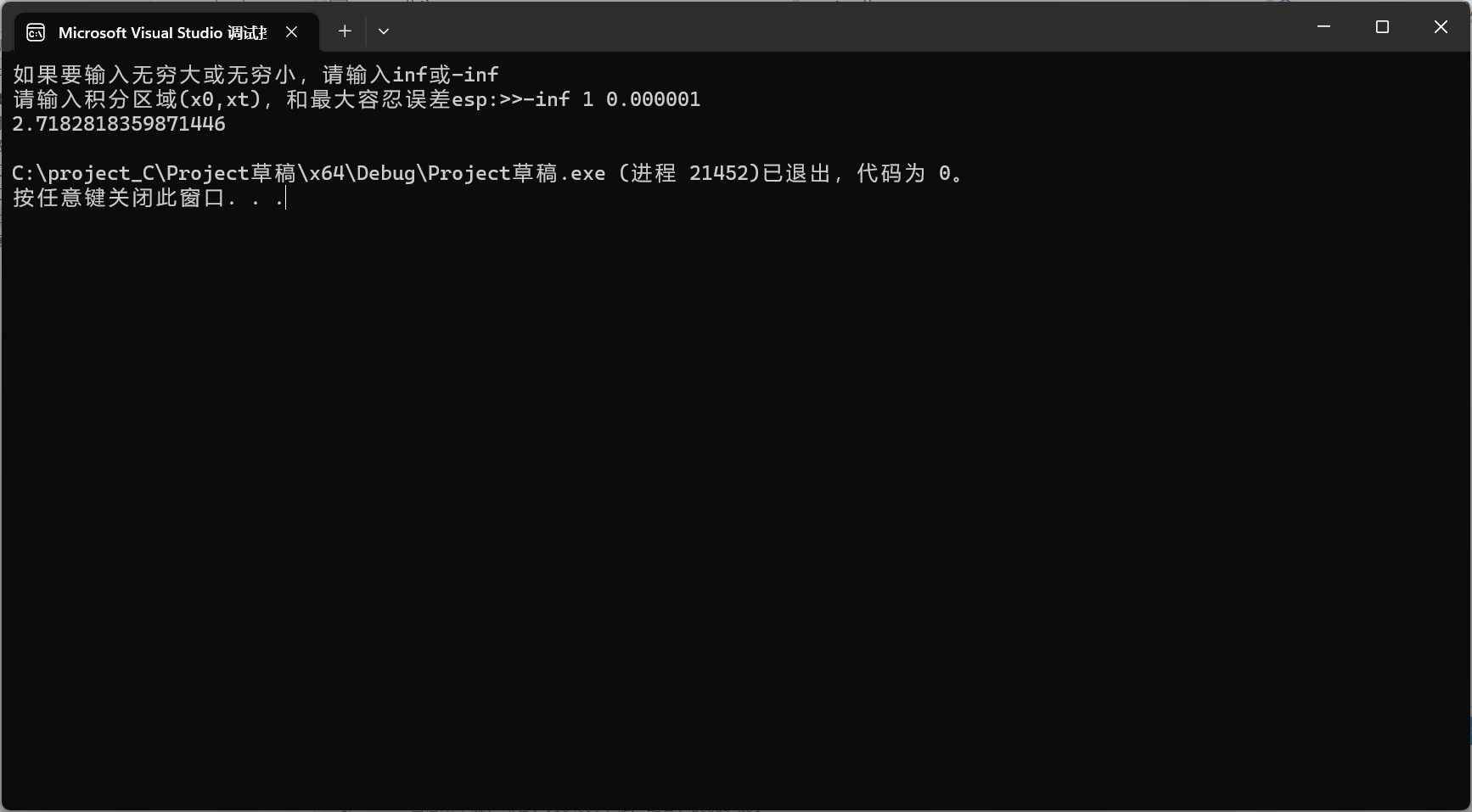
我们指定数学函数为exp(x),可以看到我们很好地计算出来该无穷积分。
相关文章:

用C语言实现定积分计算(包括无穷积分/可自定义精度)
关于严谨性的声明: 在用C语言进行定积分的计算之前,我需要声明以下几点: 一、我们所进行定积分计算的函数都是应当是黎曼可积的,这保证了我们即使均匀地分割区间也保证了积分的收敛性。 二、我们同时还应该认识到,鉴…...
使用Presto、Trino数据库时提示“The datetime zone id ‘GMT+08:00‘ is not recognised”
出现这个问题的原因是:Presto、Trino的驱动使用了joda这个库来处理时区的问题。但这个库的编写人似乎对java zone的格式没有太多经验。先看一下出错的代码: com.facebook.presto.jdbc.internal.joda.time.DateTimeZone#forID 根据String类型的zoneId转成…...

C# BeginInvoke 加 EndInvoke实现异步操作
1、定义一个委托 delegate long MyDel(int first, int second); 2、 需异步操作的函数 static int sum(int x,int y) {Console.WriteLine("InSide Sum1");Thread.Sleep(1000);Console.WriteLine("InSide Sum2");return x y;} 3、回调方法…...
)
“华为杯”研究生数学建模竞赛2015年-【华为杯】B题:数据的多流形结构分析(续)
目录 4.2.2 算法复杂度分析 4.2.3 参数影响 4.2.4 问题 3(a)求解 4.3 问题 3(b) 4.3.1 加权稀疏子空间聚类</...
R语言APSIM模型高级应用及批量模拟
随着数字农业和智慧农业的发展,基于过程的农业生产系统模型在模拟作物对气候变化的响应与适应、农田管理优化、作物品种和株型筛选、农田固碳和温室气体排放等领域扮演着越来越重要的作用。APSIM (Agricultural Production Systems sIMulator)模型是世界知名的作物生…...

【硬件设计】模拟电子基础三--集成运算放大电路
模拟电子基础三--集成运算放大电路 一、集成运算放大器1.1 定义、组成与性能1.2 电流源电路1.3 差动放大电路1.4 理想运算放大器 二、集成运算放大器的应用2.1 反向比例运算电路2.2 同向比例运算电路2.3 反向加法运算电路2.4 反向减法运算电路2.5 积分运算电路2.6 微分运算电路…...
JavaWeb(11)——前端综合案例5(小黑记事本)
一、实例需求 ⌛ 功能需求: ① 列表渲染 ② 删除功能 ③ 添加功能 ④ 底部统计 和 清空任务 二、代码实现 ☕ <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8" /> <meta http-equiv"X-UA-Compa…...

在使用TensorFlow的时候内部报错:内部某个方法或属性不存在
看到TensorFlow内部封装的方法报错的时候,我的第一反应是版本不匹配,立马去搜了对应版本,按照网上给的TensorFlow 2.2.0keras 2.3.1 python 3.7,反反复复安装、卸载、升级、降低版本了很多回还是八行,就在心态快要爆爆…...
dubbo之高可用
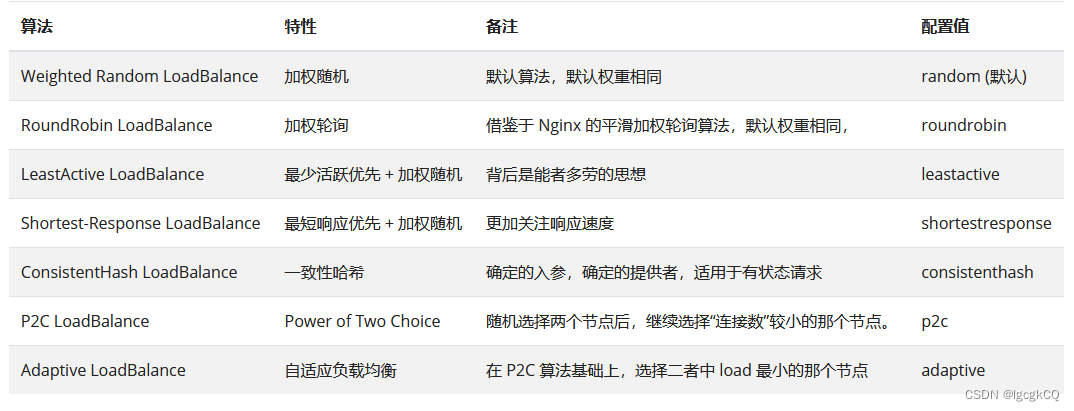
负载均衡 概述 负载均衡是指在集群中,将多个数据请求分散到不同的单元上执行,主要是为了提高系统的容错能力和对数据的处理能力。 Dubbo 负载均衡机制是决定一次服务调用使用哪个提供者的服务。 策略 在Dubbo中提供了7中负载均衡策略,默…...

gitee代码扫描js代码,降低复杂度,减少if-else判断的处理方法
把if-else换成如下形式 页面上的代码 <el-button id"btnSave" type"primary" :loading"loadingEdit" click"saveEdit(put,baseSet)"> {{ $t("formLabel.save") }} </el-button> methods代码: // 编…...

MySQL及SQL语句(3)
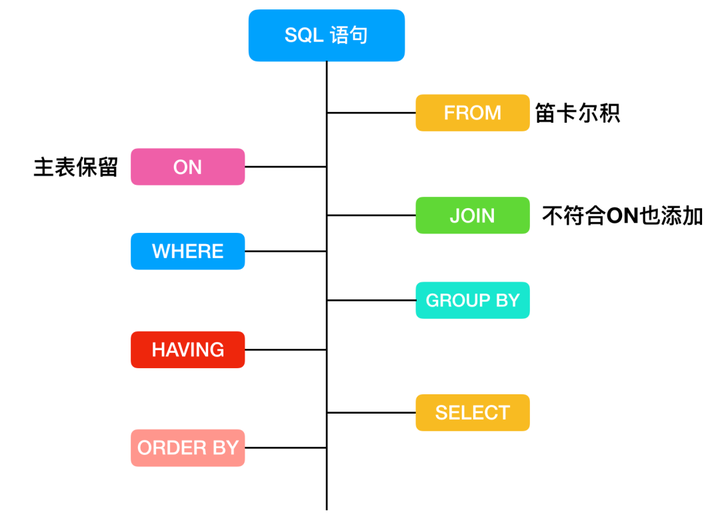
MySQL及SQL语句(3) 文章目录 MySQL及SQL语句(3)一、多表查询1.1 准备sql1.2 笛卡尔积1.3 多表查询的分类:内连接查询外连接查询子查询多表查询练习 二、事务2.1 事务的基本介绍概念操作实例事务提交的两种方式 2.2 事务的四大特征原子性持久性隔离性一致性 2.3 事务…...
MySQL 查询语句大全
目录 基础查询 直接查询 AS起别名 去重(复)查询 条件查询 算术运算符查询 逻辑运算符查询 正则表达式查询⭐ 模糊查询 范围查询 是否非空判断查询 排序查询 限制查询(分页查询) 随机查询 分组查询 HAVING 高级查询…...

【Axure高保真原型】账单列表和详情
今天和大家分享账单列表和详情的原型模板,点击月份可以展开或收起对应的菜单列表,该模板是用中继器制作的,在中继器里填写数据后,自动计算出支出和收入总和,点击订单,可以查看该订单的详情。 【原型效果】…...

嵌入式面试题1
1 读程序段,回答问题 int main(int argc, char *argv[]) { int c 9, d 0; c c % 5; d c; printf("d%d\n",d);return 0;} a) 写出程序输出 b) 在一个可移植的系统中这种表达式是否存在风险?why? 答: 1.程序输出为:…...

base64转二进制流,file文件
base64转二进制流 img标签src属性,可以直接使用base64字符串,base64需要先解码,然后再转为流 /*** Base64字符串转二进制流* param {String} dataurl Base64字符串(字符串包含Data URI scheme,例如:data:image/png;b…...
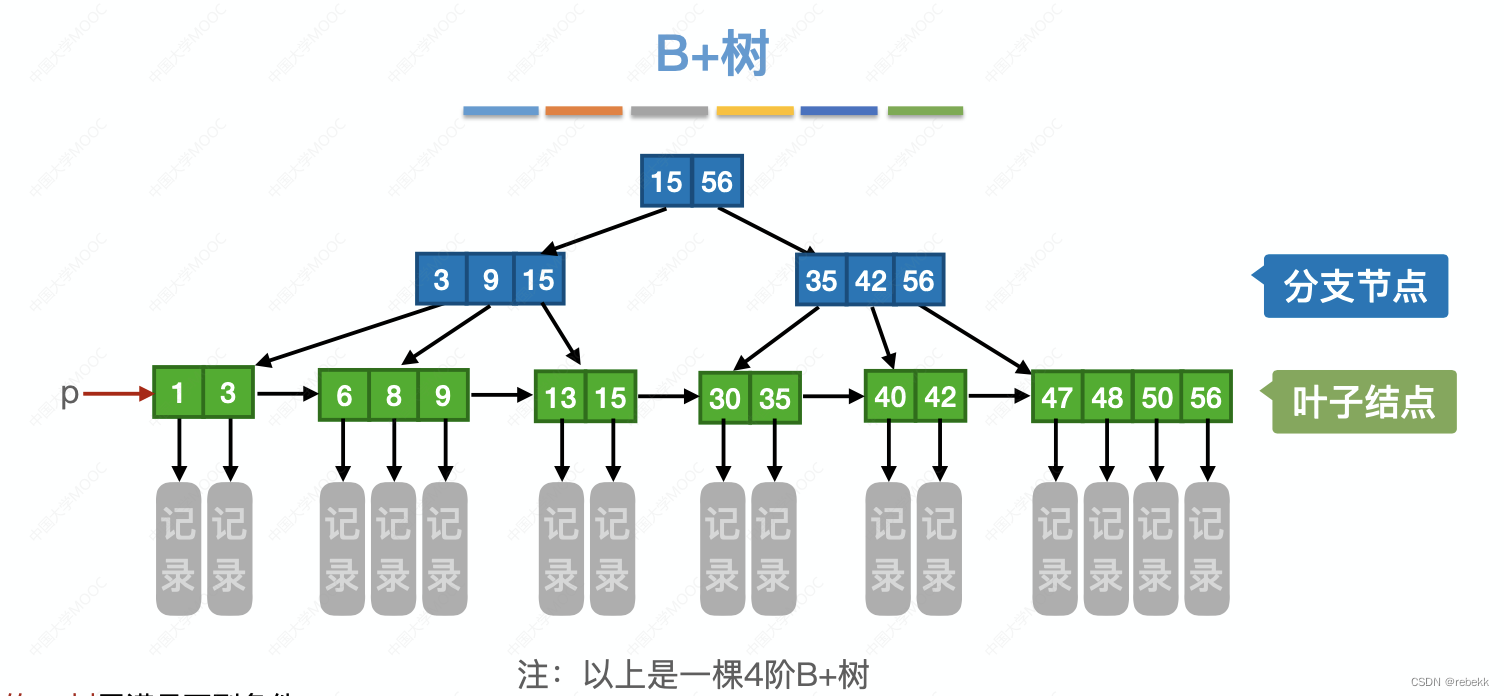
各种查找算法的效率分析
各种查找算法的效率 顺序查找 一般顺序表(没有顺序,随机排列) 成功时平均查找长度: 1 . . . n n n 1 2 \frac{1...n}{n}\frac{n1}{2} n1...n2n1失败时平均查找长度: n n n 有序顺序表(按照递增或递…...

微报告下载!市场不确定性周期下的激光雷达前装赛道
随着理想L9 Pro版本(取消激光雷达)的上市(相比AD Max版本降价3万元),中国乘用车市场仅剩下蔚来(NT2.0平台)、阿维塔11仍全系标配激光雷达。 这对于激光雷达赛道来说,是一个明确的信…...
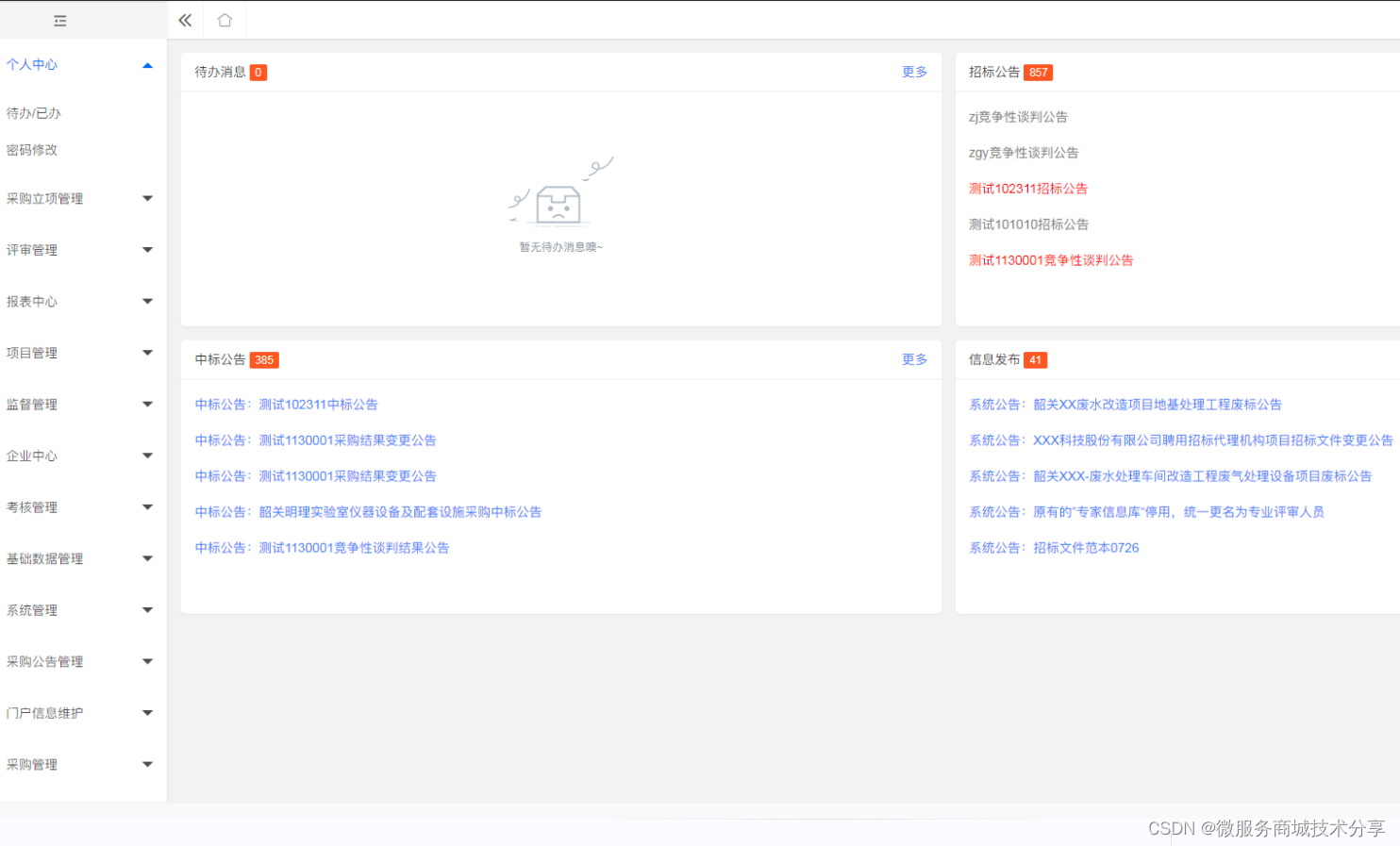
Java版企业电子招标采购系统源码Spring Cloud + Spring Boot +二次开发+ MybatisPlus + Redis tbms
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查…...
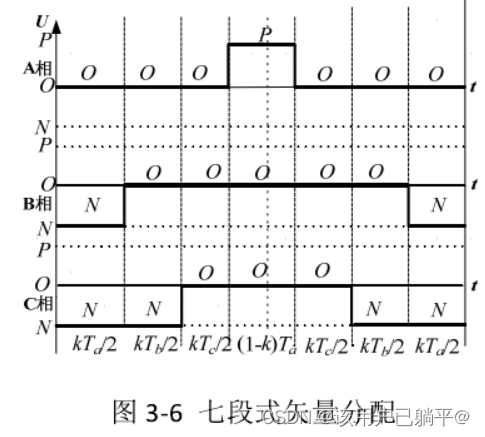
并网逆变器学习笔记6---三电平SVPWM下的连续和不连续调制
之前在学习中总结过一次DPWM策略选择:并网逆变器学习笔记5---三电平DPWM 但是对于三电平逆变器而言,如何从连续调制切换到不连续调制,存在一些疑惑点,下午闲来无事,把SVPWM下的连续调制和不连续调制的开关状态选择&am…...
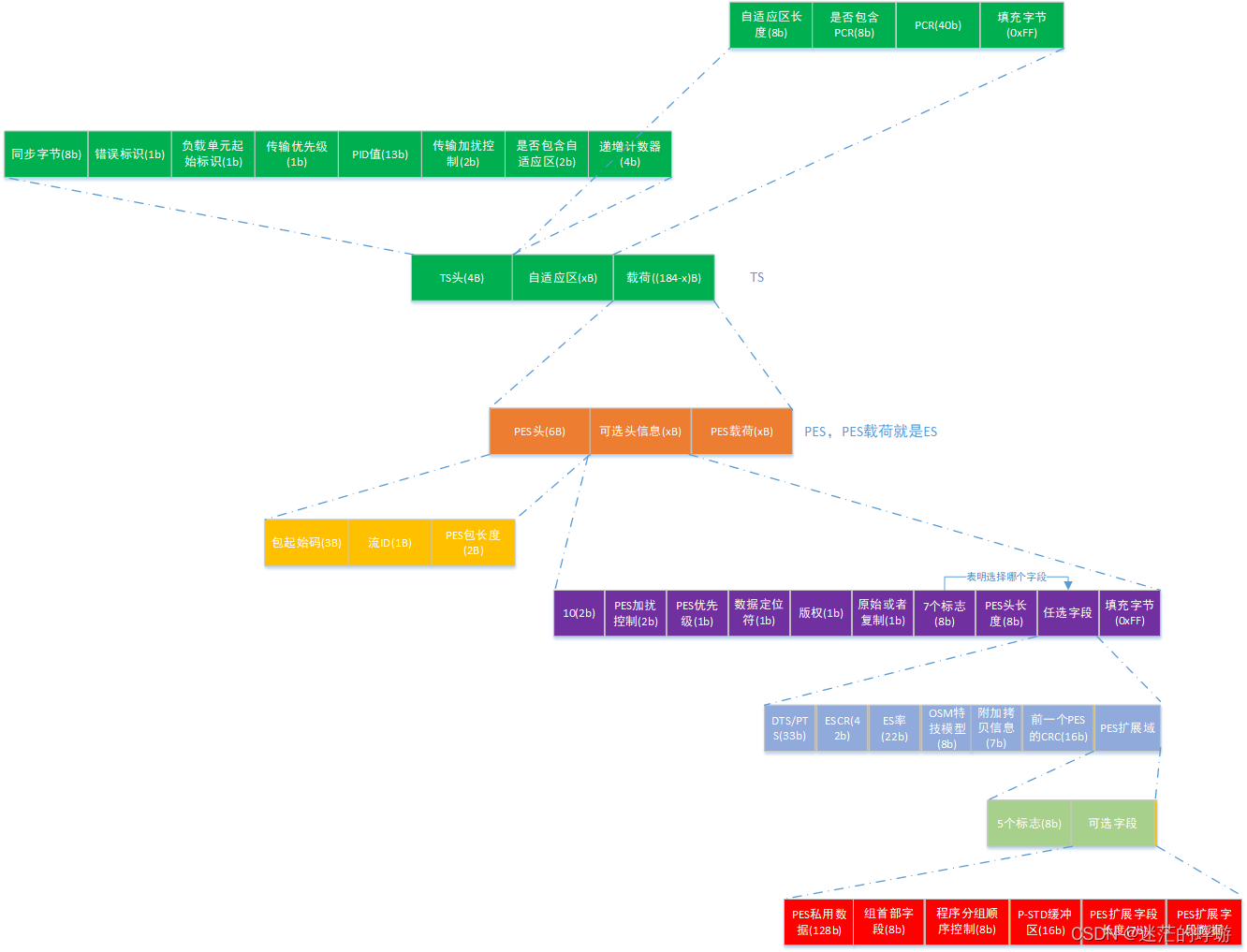
TS协议之PES(ES数据包)
TS协议之PAT(节目关联表)TS协议之PMT(节目映射表)TS协议之PES(ES数据包) 该文档已上传:下载地址 1. 概要 1.1 TS数据包(PES)协议数据组成 TSTS头PES头ES。TS…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...
