【算法篇C++实现】算法的时间、空间复杂度
文章目录
- 🚀一、算法的概念
- 🚀二、算法的特征
- 1.可行性
- 2.确定性
- 3.有穷性
- 4.输入
- 5.输出
- 🚀三、算法的评价
- 1.正确性
- 2.可读性
- 3.健壮性
- 🚀四、算法的复杂度
- ⛳(一)时间复杂度
- 1、时间复杂度的概念
- 2、大O的渐进表示法
- 3、常见时间复杂度
- ⛳(二)空间复杂度
🚀一、算法的概念
算法(algorithm)是解决一系列问题的清晰指令,也就是,能对一定规范的输入,在有限的时间内获得所要求的输出。
简单来说,算法就是解决一个问题的具体方法和步骤。算法是程序的灵魂。
程序 = 算法+数据结构
🚀二、算法的特征
1.可行性
算法中执行的任何计算步骤都可以分解为基本可执行的操作步,即每个计算步都可以在有限时间里完成(也称之为有效性)
2.确定性
算法的每一步都要有确切的意义,不能有二义性。例如“增加x的值”,并没有说增加多少,计算机就无法执行明确的运算。
3.有穷性
算法的有穷性是指算法必须在执行有限个步骤后终止。操作次数不宜过大,不能超过人们事先设定的时间限制。
4.输入
算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输入是指算法已经给出了初始条件。
5.输出
一个算法可能有1个或多个输出,以反映输入数据加工后的代码,没有输出的算法是没有意义的!
🚀三、算法的评价
通常一个好算法应该达到如下目标:
1.正确性
算法应该正确的解决问题。
2.可读性
算法应该具有较好的可读性,让人们理解算法的作用。
3.健壮性
输入非法数据时,算法也可以做出适当的反应,而不会产生奇奇怪怪的输出。
🚀四、算法的复杂度
算法复杂度是指算法在变为可执行程序后所耗费的时间资源和内存。
⛳(一)时间复杂度
1、时间复杂度的概念
评估程序所需要的时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
举例:
Func1 执行的基本操作次数 : F(N) = N^2 + 2*N + 10
当N越来越大的时候,数字的大小主要取决于N^2了。实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i)//这个循环N^2次{for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;} //这个循环2*N次int M = 10;while (M--) //这个循环10次{++count;}printf("%d\n", count);
}
2、大O的渐进表示法
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为: O(N^2)
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
3、常见时间复杂度
| 复杂度 | 标记符号 | 说明 |
|---|---|---|
| 常量 | O(1) | 操作数量为常数,与输入数据的规模无关 |
| 对数 | O(log2 n) | 与输入数据的比例是 log2(n) |
| 线性 | O(n) | 与输入数据成正比 |
| 平方 | O(n²) | 与输入数据规模的比例为平方 |
| 立方 | O(n³) | 与输入数据规模的比例为立方 |
| 指数 | O(2ⁿ)O(kⁿ)O(n!) | 快速增长,尽量减少这种代码 |
代码示范:
实例1
计算Func2的时间复杂度
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
基本操作执行了2*N + 10次,而通过推导大O阶方法,用常数1取代加法常数,得到2*N + 1,只保留最高阶项,得到2*N,将最高阶项的系数变为1,得到N
所以最后的时间复杂度是O(N)
实例2
计算Func3的时间复杂度
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}
时间复杂度为O(N+M)
实例3
计算Func4的时间复杂度
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}
用常数1替代100,时间复杂度是O(1)
实例4
计算strchr的时间复杂度
const char* strchr(const char* str, int character)
{while (*str != character){str++;}return str;
}
最快执行了1次,最慢执行了N次,所以时间复杂度是O(N)
实例5
计算BubbleSort的时间复杂度
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
第一趟冒泡排序了N - 1次,第二趟冒泡排序了N - 2次,依次类推,排序这个基本操作在最坏的情况下一共执行了(N-1)+(N-2)+…+3+2+1次比较和交换操作。使用等差数列求和的公式,可以将这个总次数简化为N(N-1)/2。,而最好的情况下是数组已经排好了,此时只需要执行N次,时间复杂度取最坏的情况,所以是O(N^2)
实例6
计算BinarySearch的时间复杂度
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}
假如有序数组有N个数,那么查找一次就会将数组的范围缩小一半,直到最后只剩下一个数
可以这么用数字表示:
N / 2 / 2 / 2 / 2 / 2 / 2 … / 2 / 2 = 1
假设查找了x次,也就是每次将数组缩小一半(除以2)这个基本操作执行了x次,那么这个x与N之间的关系是2^x = N
那么x = logN,这里默认底数为2
所以时间复杂度是O(logN)
实例7
计算阶乘递归Fac的时间复杂度
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}
基本操作递归了N次,每一层的计算时间复杂度是常数时间。所以时间复杂度为O(N)
实例8
计算斐波那契递归Fib的时间复杂度
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}

基本操作递归了约为2^N次,根据推到大O阶的方法,所以最后的时间复杂度为O(N)
⛳(二)空间复杂度
- 空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度
- 空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
- 空间复杂度一般不作考虑,一般都优先考虑时间复杂度。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
实例1
计算BubbleSort的空间复杂度
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
可见,红框标注的地方,是在函数的内部额外创建了4个变量,也就是开辟了常数个额外空间,所以空间复杂度为O(1)
实例2
计算Fibonacci的空间复杂度
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}
在动态内存中开辟了N+1个sizeof(long long)大小的空间,所以空间复杂度为O(N)
实例3
计算阶乘递归Fac的空间复杂度
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}
递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间,所以空间复杂度为O(N)
实例4
计算Fibonacci的空间复杂度
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
每一次递归调用时,每两个子函数用的函数栈帧空间都是同一个,所以只额外开辟了N个栈帧,空间复杂度为O(N)
相关文章:

【算法篇C++实现】算法的时间、空间复杂度
文章目录 🚀一、算法的概念🚀二、算法的特征1.可行性2.确定性3.有穷性4.输入5.输出 🚀三、算法的评价1.正确性2.可读性3.健壮性 🚀四、算法的复杂度⛳(一)时间复杂度1、时间复杂度的概念2、大O的渐进表示法…...

On Evaluation of Embodied Navigation Agents 论文阅读
论文信息 题目:On Evaluation of Embodied Navigation Agents 作者:Peter Anderson,Angel Chang 来源:arXiv 时间:2018 Abstract 过去两年,导航方面的创造性工作激增。这种创造性的输出产生了大量有时不…...

【CSS 布局】水平垂直方向居中
【CSS 布局】水平垂直方向居中 单行元素 <div class"container"><div class"item"></div> </div>方式一:relative 和 absolute .container {position: relative;height: 400px;border: 1px solid #ccc;.item {posit…...
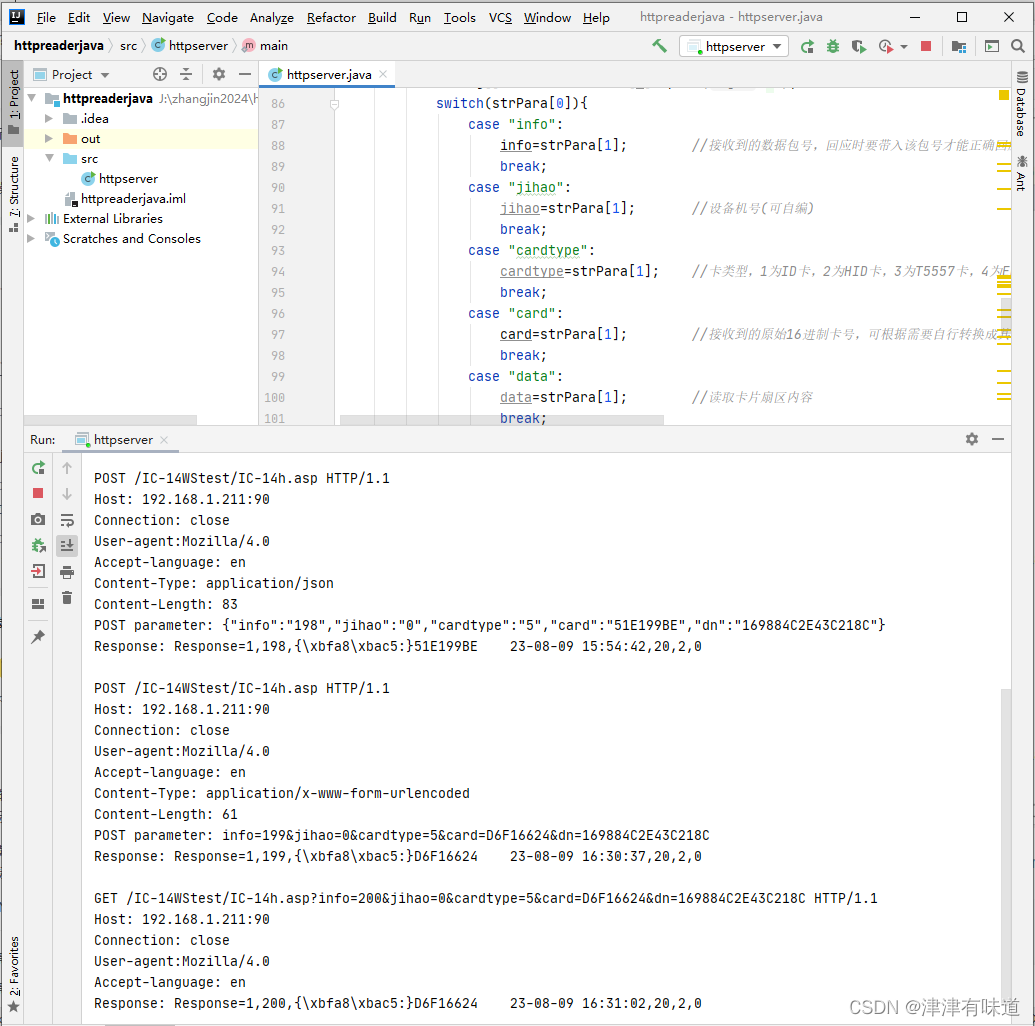
Java实现轻量型Web服务器接收http协议提交的RFID读卡信息
示例使用的读卡器:RFID网络WIFI无线TCP/UDP/HTTP可编程二次开发读卡器POE供电语音-淘宝网 (taobao.com) import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.io.PrintWriter; import java.net.ServerSock…...

模拟实现消息队列项目(完结) -- 基于MQ的生产者消费者模型
目录 前言 1. 生产者 2. 消费者 3. 启动消息队列服务器 4. 运行效果 结语 前言 在上一章节,我们完成了消息队列的客户端部分,至此我们整个消息队列项目就构建完成了,那我们做的这个消息队列到底有什么效果,以及如何去使用我们自己的消息队列呢?那么本文,就将我们的MQ进行实战操…...

专业商城财务一体化-线上商城+进销存管理软件,批发零售全行业免费更新
订货流程繁琐?订单处理效率低?小程序商城与进销存系统不打通?数据需要手动输入同步?财务与的结算对账需要大量手工处理?零售批发从业者,如何你也有以上烦恼,可以看看进销存小程序订货商城&#…...

深度思考mysql面经
推荐 1 索引下推 Mysql性能优化:什么是索引下推? 1.1 定义 索引下推(Index Condition Pushdown,简称 ICP)是一种数据库优化技术。在传统的数据库查询中,数据库首先使用索引检索来找到符合索引条件的行&…...

2023-08-09力扣每日一题
链接: 1281. 整数的各位积和之差 题意: 十进制每一位的积减去每一位的和 解: 十进制位处理 实际代码: #include<iostream> using namespace std; int subtractProductAndSum(int n) {int t11,t20;while(n){t1*n%10;t…...

[23] Instruct 3D-to-3D: Text Instruction Guided 3D-to-3D conversion
本文提出一种3D-to-3D转换方法:Instruct 3D-to-3D;借助预训练的Image-to-Image扩散模型,本文方法可以使各个视角图片的似然最大;本文方法显式地将source 3D场景作为condition,可以有效提升3D连续性和可控性。同时&…...
设计模式行为型——访问者模式
目录 访问者模式的定义 访问者模式的实现 访问者模式角色 访问者模式类图 访问者模式举例 访问者模式代码实现 访问者模式的特点 优点 缺点 使用场景 注意事项 实际应用 访问者模式的定义 访问者模式(Visitor Pattern)属于行为型设计模式&am…...

vue3官网文档学习、复习笔记(快速上手)
目录 2.Attribute 绑定(v-bind) 3.事件监听(v-on) 4.表单绑定(v-model) 5.条件渲染(v-if) 6.列表渲染(v-for) all.value all.value.filter(…...
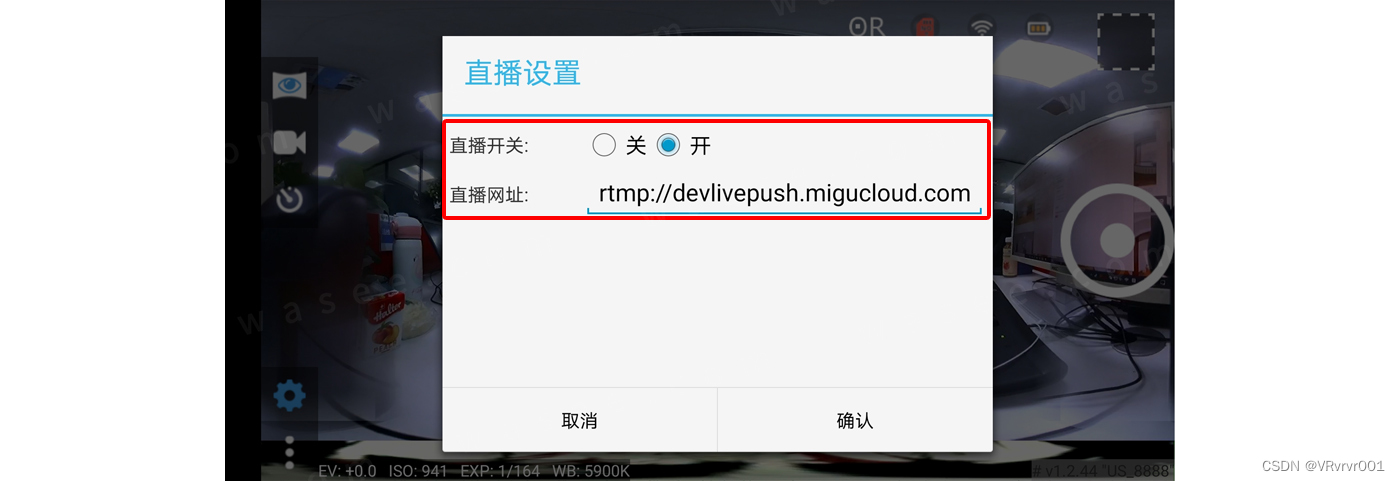
0基础学习VR全景平台篇 第81篇:全景相机-临云镜如何直播推流
临云镜全景相机是阿里巴巴定制全景设备,实现空间三维信息的快速采集,与阿里云三维空间重建平台搭配,帮助品牌商与平台以较低的成本完成空间的快速采集,并支持对室内/室外空间的三维全景展示及空间漫游,同时支持VR浏览、…...

分数线划定
题目描述 查看题目信息 世博会志愿者的选拔工作正在A 市如火如荼的进行。为了选拔最合适的人才,A 市对所有报名的选手进行了笔试,笔试分数达到面试分数线的选手方可进入面试。 面试分数线根据计划录取人数的150%划定,即如果计划录取m名志愿…...

考研C语言进阶题库——更新26-30题
目录 26.一个正整数,如果等于组成它的各个数字的阶数之和,该整数称为阶乘合数,例如1451阶加四阶加五阶,则145是一个三位阶乘合数,输入一个数,问共有多少个阶乘合数?(十万之内) 27.与2相关的数…...
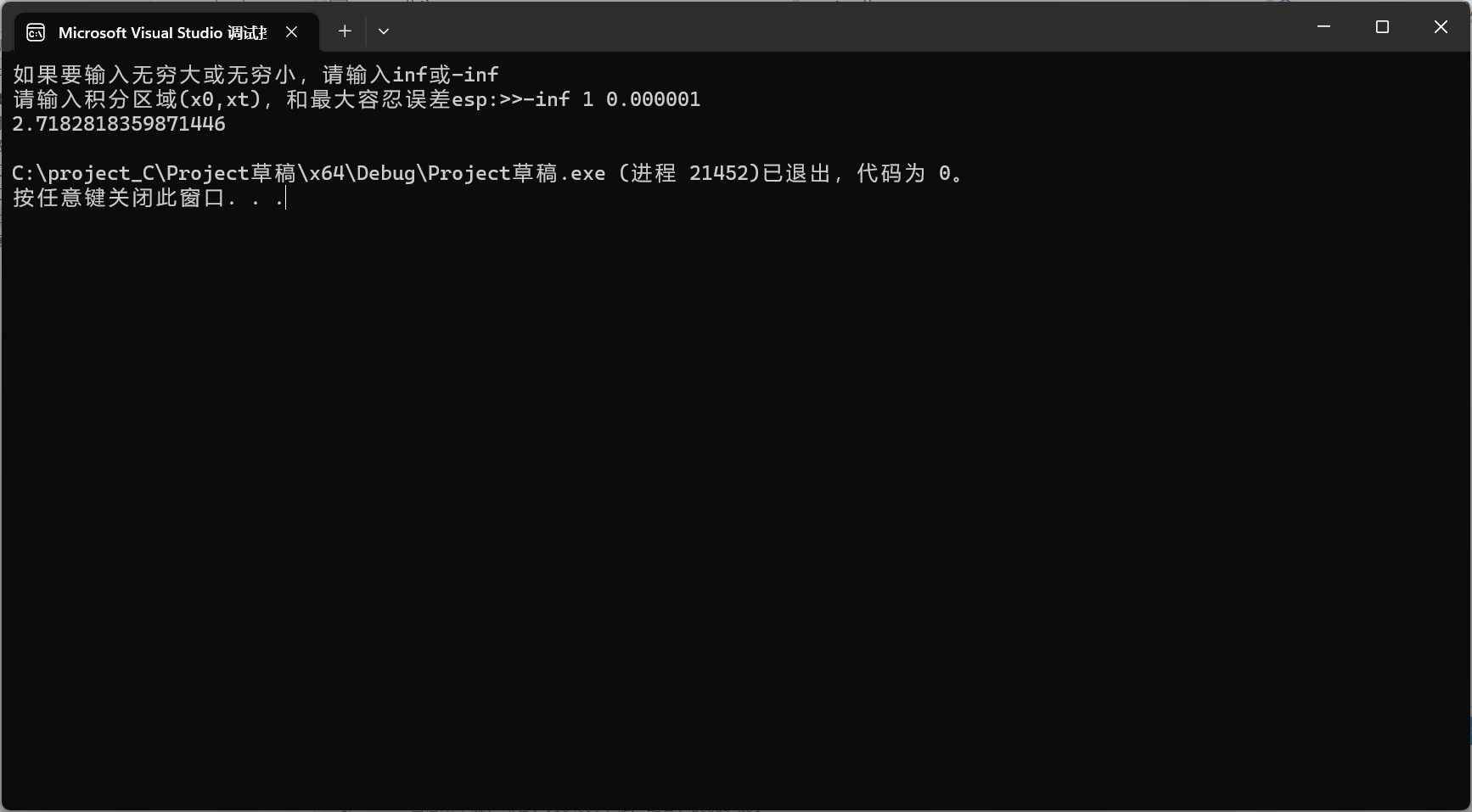
用C语言实现定积分计算(包括无穷积分/可自定义精度)
关于严谨性的声明: 在用C语言进行定积分的计算之前,我需要声明以下几点: 一、我们所进行定积分计算的函数都是应当是黎曼可积的,这保证了我们即使均匀地分割区间也保证了积分的收敛性。 二、我们同时还应该认识到,鉴…...
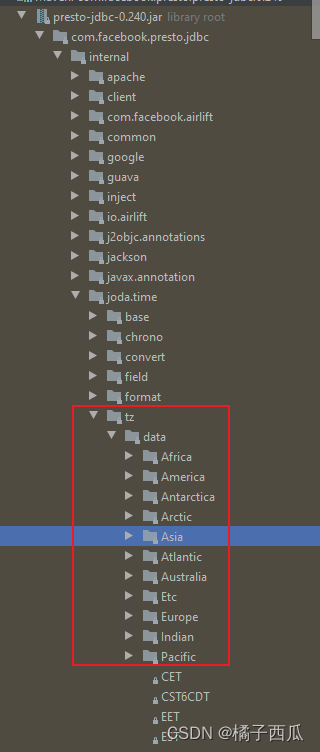
使用Presto、Trino数据库时提示“The datetime zone id ‘GMT+08:00‘ is not recognised”
出现这个问题的原因是:Presto、Trino的驱动使用了joda这个库来处理时区的问题。但这个库的编写人似乎对java zone的格式没有太多经验。先看一下出错的代码: com.facebook.presto.jdbc.internal.joda.time.DateTimeZone#forID 根据String类型的zoneId转成…...

C# BeginInvoke 加 EndInvoke实现异步操作
1、定义一个委托 delegate long MyDel(int first, int second); 2、 需异步操作的函数 static int sum(int x,int y) {Console.WriteLine("InSide Sum1");Thread.Sleep(1000);Console.WriteLine("InSide Sum2");return x y;} 3、回调方法…...
)
“华为杯”研究生数学建模竞赛2015年-【华为杯】B题:数据的多流形结构分析(续)
目录 4.2.2 算法复杂度分析 4.2.3 参数影响 4.2.4 问题 3(a)求解 4.3 问题 3(b) 4.3.1 加权稀疏子空间聚类</...
R语言APSIM模型高级应用及批量模拟
随着数字农业和智慧农业的发展,基于过程的农业生产系统模型在模拟作物对气候变化的响应与适应、农田管理优化、作物品种和株型筛选、农田固碳和温室气体排放等领域扮演着越来越重要的作用。APSIM (Agricultural Production Systems sIMulator)模型是世界知名的作物生…...

【硬件设计】模拟电子基础三--集成运算放大电路
模拟电子基础三--集成运算放大电路 一、集成运算放大器1.1 定义、组成与性能1.2 电流源电路1.3 差动放大电路1.4 理想运算放大器 二、集成运算放大器的应用2.1 反向比例运算电路2.2 同向比例运算电路2.3 反向加法运算电路2.4 反向减法运算电路2.5 积分运算电路2.6 微分运算电路…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
