分数线划定
题目描述
查看题目信息
世博会志愿者的选拔工作正在A 市如火如荼的进行。为了选拔最合适的人才,A 市对所有报名的选手进行了笔试,笔试分数达到面试分数线的选手方可进入面试。
面试分数线根据计划录取人数的150%划定,即如果计划录取m名志愿者,则面试分数线为排名第m*150%(向下取整)名的选手的分数,而最终进入面试的选手为笔试成绩不低于面试分数线的所有选手。
现在就请你编写程序划定面试分数线,并输出所有进入面试的选手的报名号和笔试成绩。
输入格式
第一行,两个整数n,m(5 ≤ n ≤ 5000,3 ≤ m ≤ n),中间用一个空格隔开,其中n 表示报名参加笔试的选手总数,m 表示计划录取的志愿者人数。输入数据保证m*150%向下取整后小于等于n。
第二行到第n+1 行,每行包括两个整数,中间用一个空格隔开,分别是选手的报名号k(1000 ≤ k ≤ 9999)和该选手的笔试成绩s(1 ≤ s ≤ 100)。数据保证选手的报名号各不相同。
输出格式
第一行,有两个整数,用一个空格隔开,第一个整数表示面试分数线;第二个整数为进入面试的选手的实际人数。
从第二行开始,每行包含两个整数,中间用一个空格隔开,分别表示进入面试的选手的报名号和笔试成绩,按照笔试成绩从高到低输出,如果成绩相同,则按报名号由小到大的顺序输出。
样例输入
6 3 1000 90 3239 88 2390 95 7231 84 1005 95 1001 88
样例输出
88 5 1005 95 2390 95 1000 90 1001 88 3239 88
参考代码
#include <iostream>
#include <algorithm>
using namespace std;struct student
{int fs;int xh;bool flag;
};student a[5005];bool cmp(student x, student y)
{if(x.fs > y.fs)return true;else if(x.fs == y.fs){if(x.xh < y.xh)return true;}return false;
}int main()
{int n, m, i, fsx = 0, lss = 0;cin>>n>>m;for(i = 1; i <= n; i++){cin>>a[i].xh>>a[i].fs;a[i].flag = false;}fsx = m * 1.5;sort(a + 1, a + n + 1, cmp);for(i = fsx + 1; i <= n; i++){if(a[fsx].fs == a[i].fs )lss++;}cout<<a[fsx].fs<<" "<<fsx + lss<<endl;for(i = 1; i <= fsx + lss; i++){cout<<a[i].xh<<" "<<a[i].fs<<endl;}return 0;
} 相关文章:

分数线划定
题目描述 查看题目信息 世博会志愿者的选拔工作正在A 市如火如荼的进行。为了选拔最合适的人才,A 市对所有报名的选手进行了笔试,笔试分数达到面试分数线的选手方可进入面试。 面试分数线根据计划录取人数的150%划定,即如果计划录取m名志愿…...

考研C语言进阶题库——更新26-30题
目录 26.一个正整数,如果等于组成它的各个数字的阶数之和,该整数称为阶乘合数,例如1451阶加四阶加五阶,则145是一个三位阶乘合数,输入一个数,问共有多少个阶乘合数?(十万之内) 27.与2相关的数…...
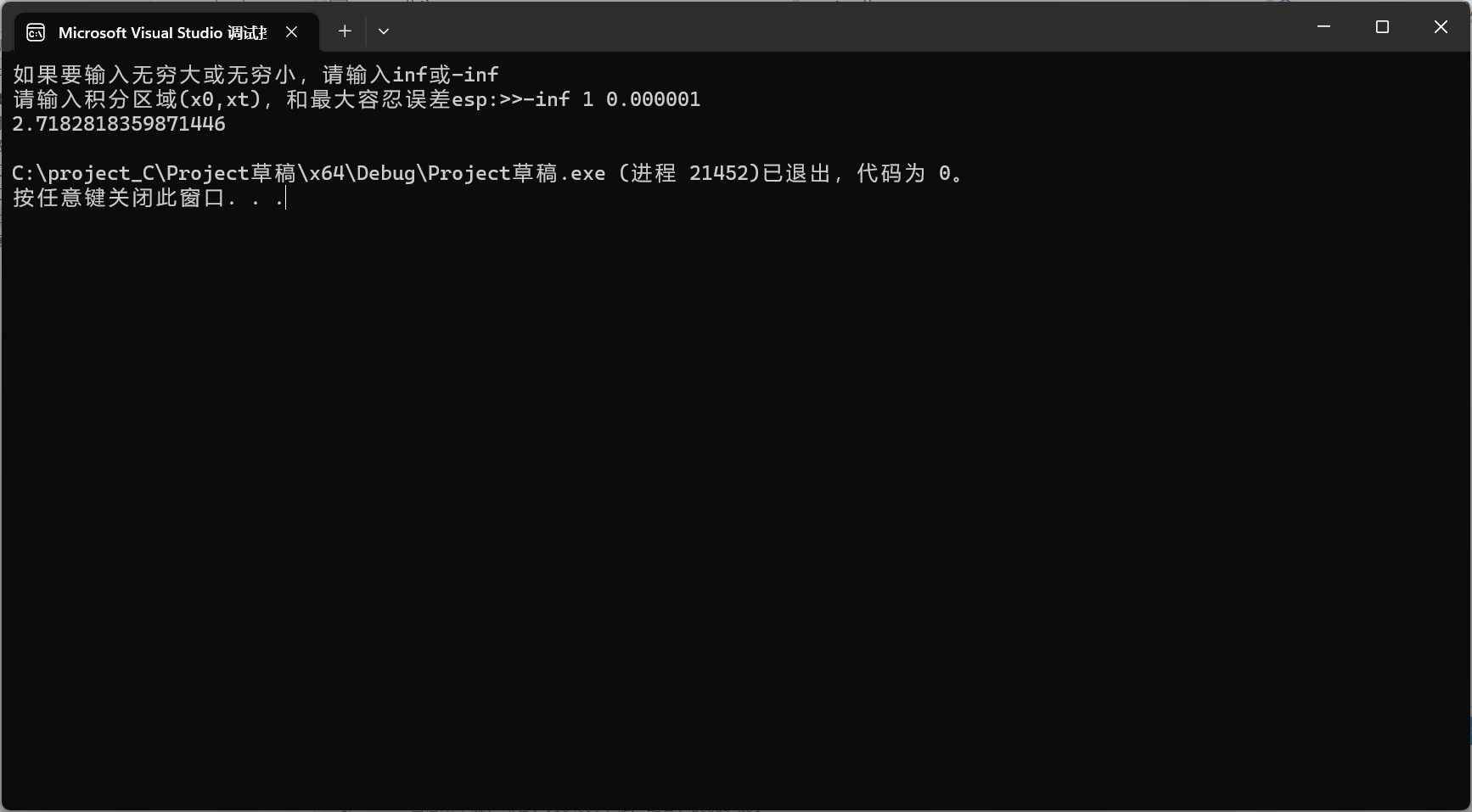
用C语言实现定积分计算(包括无穷积分/可自定义精度)
关于严谨性的声明: 在用C语言进行定积分的计算之前,我需要声明以下几点: 一、我们所进行定积分计算的函数都是应当是黎曼可积的,这保证了我们即使均匀地分割区间也保证了积分的收敛性。 二、我们同时还应该认识到,鉴…...
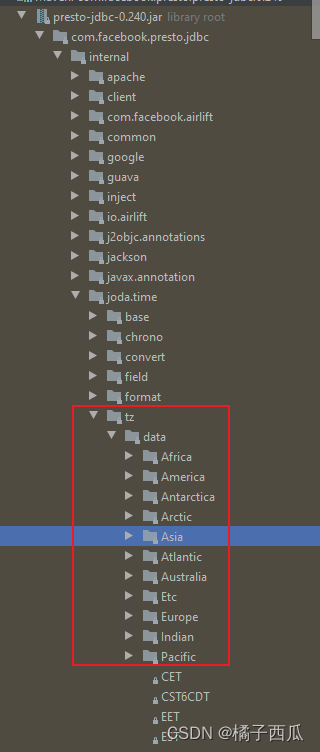
使用Presto、Trino数据库时提示“The datetime zone id ‘GMT+08:00‘ is not recognised”
出现这个问题的原因是:Presto、Trino的驱动使用了joda这个库来处理时区的问题。但这个库的编写人似乎对java zone的格式没有太多经验。先看一下出错的代码: com.facebook.presto.jdbc.internal.joda.time.DateTimeZone#forID 根据String类型的zoneId转成…...

C# BeginInvoke 加 EndInvoke实现异步操作
1、定义一个委托 delegate long MyDel(int first, int second); 2、 需异步操作的函数 static int sum(int x,int y) {Console.WriteLine("InSide Sum1");Thread.Sleep(1000);Console.WriteLine("InSide Sum2");return x y;} 3、回调方法…...
)
“华为杯”研究生数学建模竞赛2015年-【华为杯】B题:数据的多流形结构分析(续)
目录 4.2.2 算法复杂度分析 4.2.3 参数影响 4.2.4 问题 3(a)求解 4.3 问题 3(b) 4.3.1 加权稀疏子空间聚类</...
R语言APSIM模型高级应用及批量模拟
随着数字农业和智慧农业的发展,基于过程的农业生产系统模型在模拟作物对气候变化的响应与适应、农田管理优化、作物品种和株型筛选、农田固碳和温室气体排放等领域扮演着越来越重要的作用。APSIM (Agricultural Production Systems sIMulator)模型是世界知名的作物生…...

【硬件设计】模拟电子基础三--集成运算放大电路
模拟电子基础三--集成运算放大电路 一、集成运算放大器1.1 定义、组成与性能1.2 电流源电路1.3 差动放大电路1.4 理想运算放大器 二、集成运算放大器的应用2.1 反向比例运算电路2.2 同向比例运算电路2.3 反向加法运算电路2.4 反向减法运算电路2.5 积分运算电路2.6 微分运算电路…...
JavaWeb(11)——前端综合案例5(小黑记事本)
一、实例需求 ⌛ 功能需求: ① 列表渲染 ② 删除功能 ③ 添加功能 ④ 底部统计 和 清空任务 二、代码实现 ☕ <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8" /> <meta http-equiv"X-UA-Compa…...

在使用TensorFlow的时候内部报错:内部某个方法或属性不存在
看到TensorFlow内部封装的方法报错的时候,我的第一反应是版本不匹配,立马去搜了对应版本,按照网上给的TensorFlow 2.2.0keras 2.3.1 python 3.7,反反复复安装、卸载、升级、降低版本了很多回还是八行,就在心态快要爆爆…...
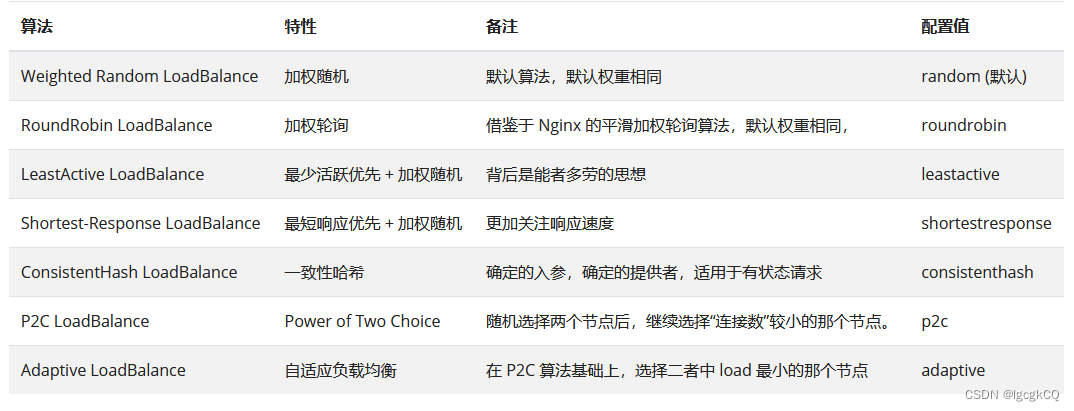
dubbo之高可用
负载均衡 概述 负载均衡是指在集群中,将多个数据请求分散到不同的单元上执行,主要是为了提高系统的容错能力和对数据的处理能力。 Dubbo 负载均衡机制是决定一次服务调用使用哪个提供者的服务。 策略 在Dubbo中提供了7中负载均衡策略,默…...

gitee代码扫描js代码,降低复杂度,减少if-else判断的处理方法
把if-else换成如下形式 页面上的代码 <el-button id"btnSave" type"primary" :loading"loadingEdit" click"saveEdit(put,baseSet)"> {{ $t("formLabel.save") }} </el-button> methods代码: // 编…...

MySQL及SQL语句(3)
MySQL及SQL语句(3) 文章目录 MySQL及SQL语句(3)一、多表查询1.1 准备sql1.2 笛卡尔积1.3 多表查询的分类:内连接查询外连接查询子查询多表查询练习 二、事务2.1 事务的基本介绍概念操作实例事务提交的两种方式 2.2 事务的四大特征原子性持久性隔离性一致性 2.3 事务…...
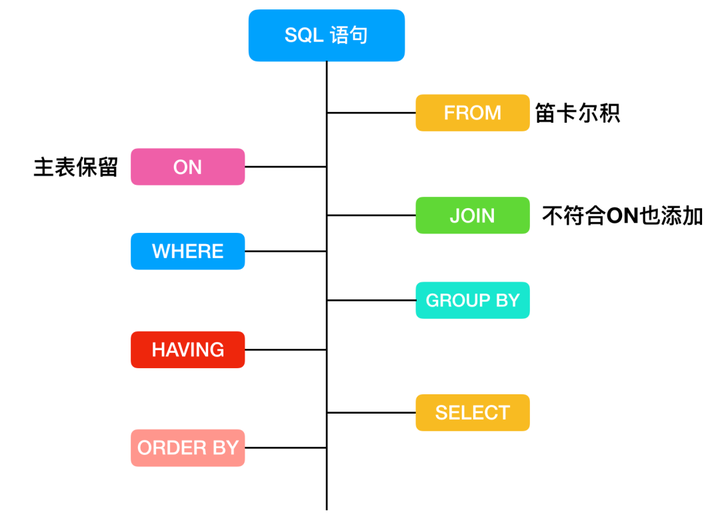
MySQL 查询语句大全
目录 基础查询 直接查询 AS起别名 去重(复)查询 条件查询 算术运算符查询 逻辑运算符查询 正则表达式查询⭐ 模糊查询 范围查询 是否非空判断查询 排序查询 限制查询(分页查询) 随机查询 分组查询 HAVING 高级查询…...

【Axure高保真原型】账单列表和详情
今天和大家分享账单列表和详情的原型模板,点击月份可以展开或收起对应的菜单列表,该模板是用中继器制作的,在中继器里填写数据后,自动计算出支出和收入总和,点击订单,可以查看该订单的详情。 【原型效果】…...

嵌入式面试题1
1 读程序段,回答问题 int main(int argc, char *argv[]) { int c 9, d 0; c c % 5; d c; printf("d%d\n",d);return 0;} a) 写出程序输出 b) 在一个可移植的系统中这种表达式是否存在风险?why? 答: 1.程序输出为:…...

base64转二进制流,file文件
base64转二进制流 img标签src属性,可以直接使用base64字符串,base64需要先解码,然后再转为流 /*** Base64字符串转二进制流* param {String} dataurl Base64字符串(字符串包含Data URI scheme,例如:data:image/png;b…...
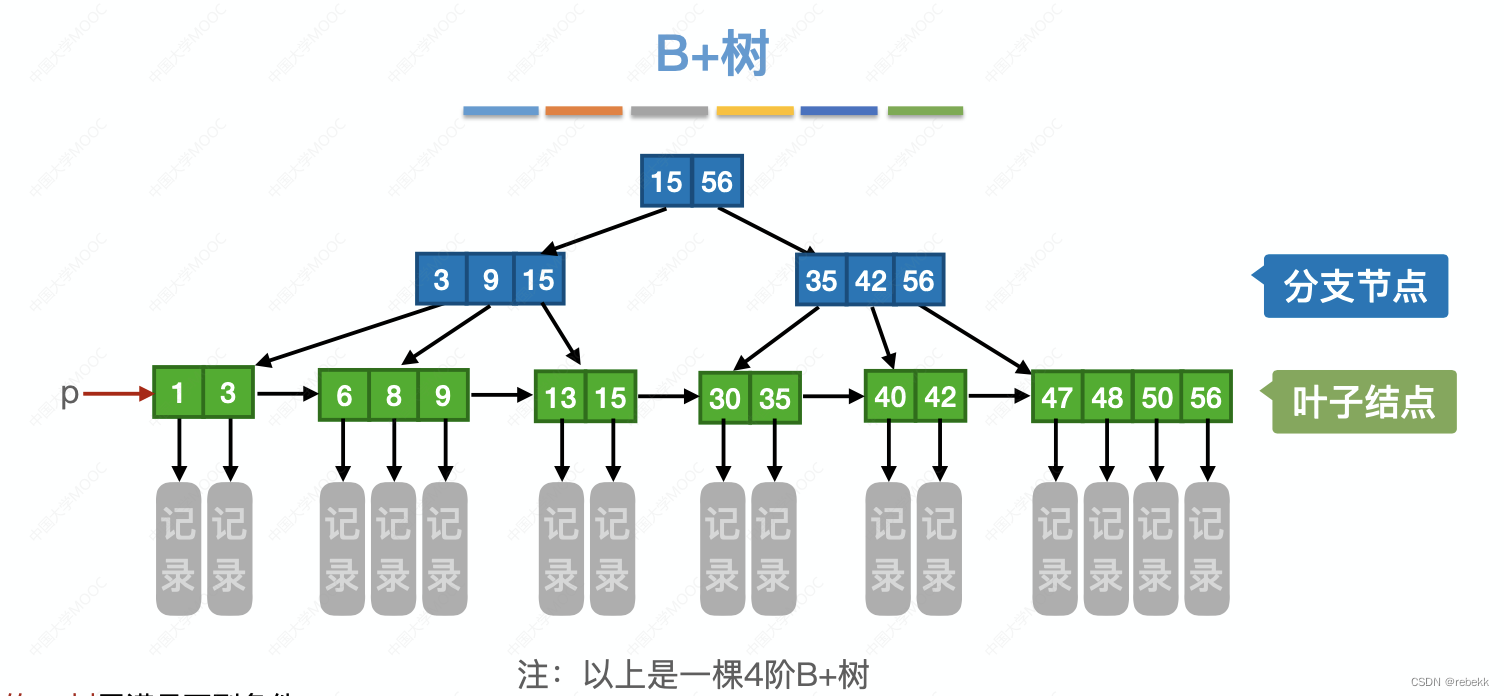
各种查找算法的效率分析
各种查找算法的效率 顺序查找 一般顺序表(没有顺序,随机排列) 成功时平均查找长度: 1 . . . n n n 1 2 \frac{1...n}{n}\frac{n1}{2} n1...n2n1失败时平均查找长度: n n n 有序顺序表(按照递增或递…...

微报告下载!市场不确定性周期下的激光雷达前装赛道
随着理想L9 Pro版本(取消激光雷达)的上市(相比AD Max版本降价3万元),中国乘用车市场仅剩下蔚来(NT2.0平台)、阿维塔11仍全系标配激光雷达。 这对于激光雷达赛道来说,是一个明确的信…...
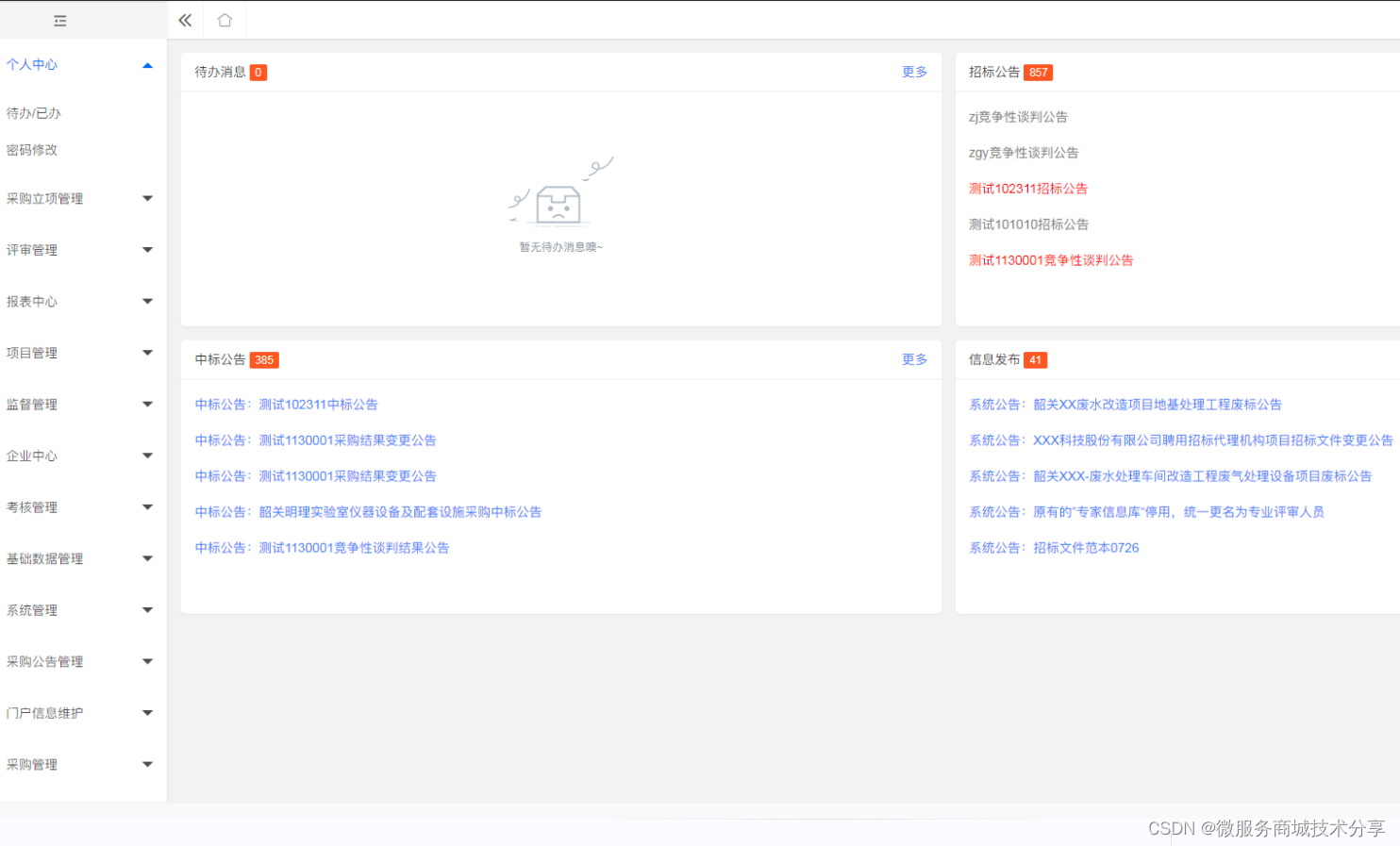
Java版企业电子招标采购系统源码Spring Cloud + Spring Boot +二次开发+ MybatisPlus + Redis tbms
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
