期权定价模型系列【1】—BSM通用式模型
这是期权定价模型专栏的第一篇文章,此专栏旨在分享一些期权定价模型,将会从最基础的BSM模型开始写起,逐步扩散到蒙特卡洛模拟、二叉树等数值法模型,以及跳跃扩散模型、随机波动率模型,神经网络模型等等。
如果你觉得有帮助,不妨点赞收藏支持一下哦。
1.前言
1973年BSM模型首次发表后便很快被应用到了金融市场中。交易商用BSM模型对期权进行定价,并进一步推动了期权在不同市场上的应用。自BSM模型开始,市场首次找到了理论上可靠的期权定价模型,这大大推动了整个期权市场的发展,反过来也促进了标的资产市场的定价和流动性。
在某种意义上,BSM模型确实是个奇迹:它使得你可以用一种非常理性的方法来给证券定价,在此之前,根本没有一个合理的或者站得住脚的定价理论。一个完全理想化的世界中(假设回报服从正态分布,股票价格服从几何布朗运动规律,具有充沛的流动性,可以进行持续套期保值,并且没有交易成本),BSM模型提供了一种动态复制期权的方法。这是一个在想象世界中工程学方法所创造的杰作,只是这个世界并不存在,因为市场并不总是服从所有的假设条件。这确实是个奇迹,但是它也只是一个模型,并不是实际情况。
当然,BSM模型所要求的假设条件非常严苛:假设标的资产的回报服从正态分布、价格服从几何布朗运动、市场始终可以提供充沛的流动性、可以进行无成本的连续对冲交易等。在真实的市场中,这些假设条件有一些可以近似满足,还有一些就相距甚远。比如,交易成本和连续对冲,可以通过调整假设条件来实现。还有一些,比如股票价格变动的模式,就很难服从几何布朗运动的假设。在现实中,股票价格经常会出现跳跃,整体分布呈现肥尾,甚至波动率也会出现完全无法预计的变动,这些条件就很难通过调整假设条件来解决。
2.静态复制
首先,通过期权定义可以很容易得到一个普通欧式看涨期权与看跌期权在到期日的合约价值为:

那么,假设投资者买入一个欧式看涨期权,同时卖出一个行权价相同的欧式看跌期权,那么无论到期日股票的最终价格是多少,投资者能获得收益都是确定的:(ST-K)。
更进一步,假设股票在未来没有分红。在到期日之前的某个时间t,如果投资者按照当前价格St买入一份标的股票,同时卖出Ke-r(T-t)份无风险债券,那么在T时刻,这个组合的价值就是(ST-K)。根据一价定律可知,一个是买入欧式看涨期权,同时卖出行权价相等的欧式看跌期权,一个是买入股票,同时卖出无风险债券,这两者当前的价格应该是相等的,即为:

通过对上式两边进行移项,要复制一个看涨期权只需要一个行权价和到期日都相同的看跌期权、标的股票以及无风险债券。要复制一个看跌期权,只需要一个行权价格和到期日都相同的看涨期权、标的股票以及无风险债券
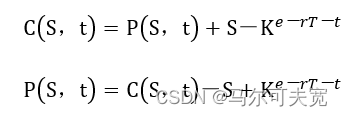
3.模型推导
运用复制的方法进行估值是整个布莱克-斯科尔斯-默顿(BSM)期权定价模型的理论基础。在推导BSM模型的时候,需要进行一系列的理论假设:标的股票价格的变化是连续的,波动率为常数并且没有价格跳跃(单因子布朗运动);交易员可以通过大额多头或空头头寸进行持续对冲;没有买卖差价;没有交易成本;可以自主决定头寸调整。
假设在t时刻,某股票的价格为S,其波动率为常数σS,预期回报为μS。同时,还存在一只无风险债券,其价格为B,收益率假设为常数r。股票和债券的随机价格服从:

其中,dZ服从标准维纳过程。以该股票为标的资产的看涨期权在t时刻的价格C,是一个跟股票价格和时间相关的变量。根据伊藤引理,C的价格等于:
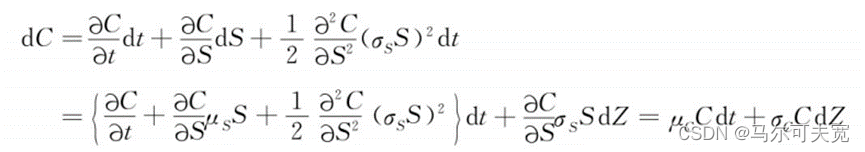
其中有:
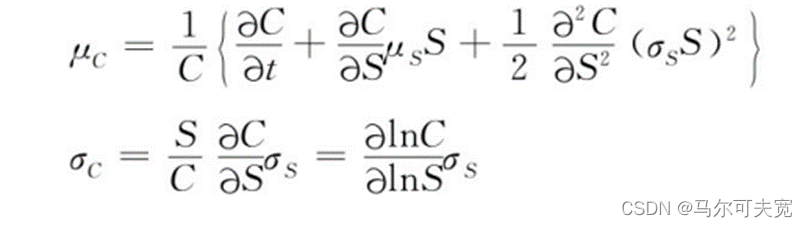
将S和C的头寸结合在一起,构建一个持续的无风险组合,消除该风险变量。令π=αS+C,其中α表示在t时刻对冲期权风险所需的股票数量。那么就有:
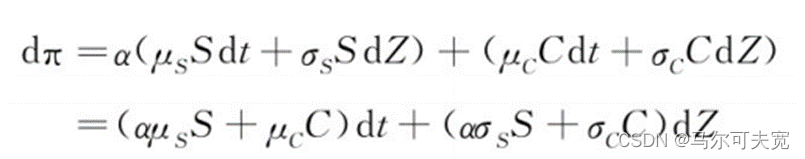
要使这个组合保持瞬时无风险,随机变量dZ的协方差就必须要等于0。也就是:

其中:
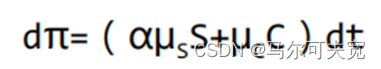
由于这个组合在t时刻也是无风险的,根据一价定律,在t时刻其收益率也应该是无风险利率r,所以就有:

在对冲组合中,这相当于:
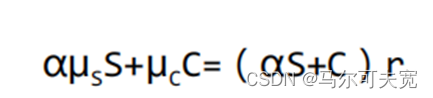
进行移项调整后有:

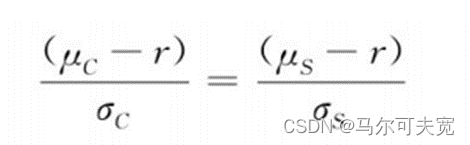
看涨期权和标的股票的瞬时夏普比率相等。如果不存在无风险套利的机会,那么对股票和期权来说,每单位波动率对应的超额回报是相等的。这也是布莱克和斯科尔斯最开始在推导BSM等式时提出的观点。继续进行计算,替换μC和σC有:
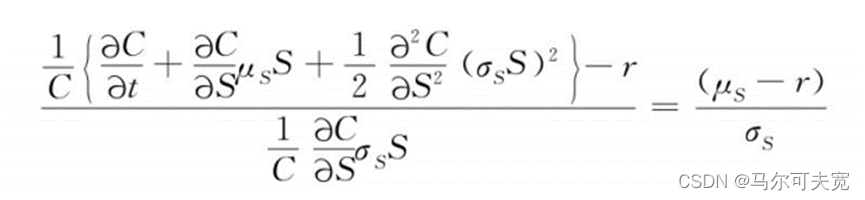
可得BSM模型的偏微分方程式:
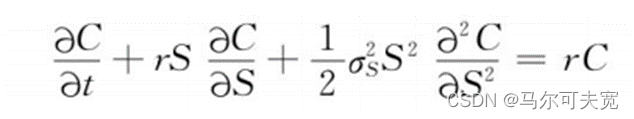
4.BSM模型
BSM模型是由Black和Scholes推导出来的可以被用于到期前不分红的欧式股票期权的估值模型,假定c和p分为代表欧式看涨与欧式看跌期权的价格,则期权的定价公式为:
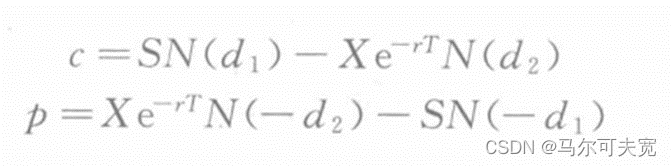
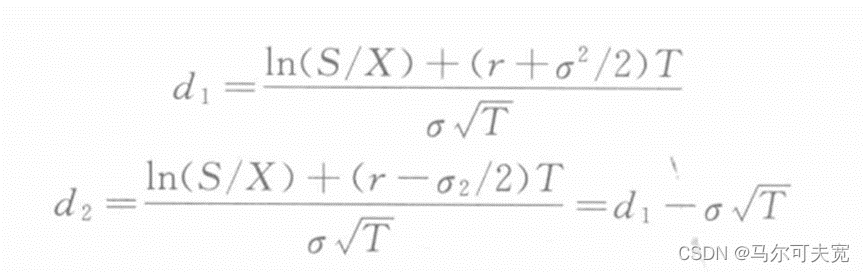
参数释义如下:

5.股指期权定价模型
Merton将BS模型扩展到允许支付连续股息的情景,这一模型可以用于支付已知连续股息率q的股票或者股指的欧式看涨、欧式看跌期权的定价问题。
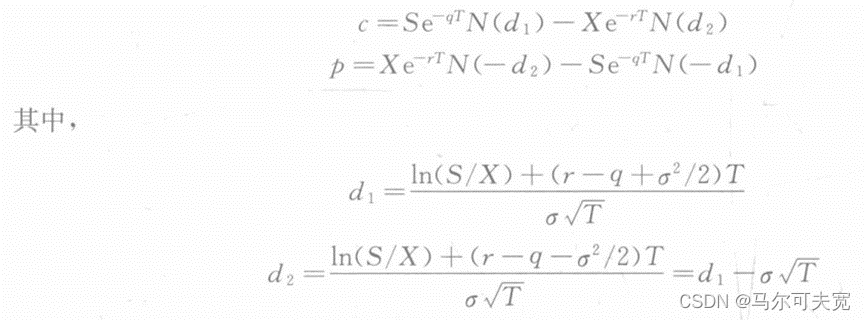
6.期货期权定价模型
Black在1976年给出了用于为标的资产为远期或者期货合约定价的欧式看涨、欧式看跌期权定价模型,假设标的资产价格为F。
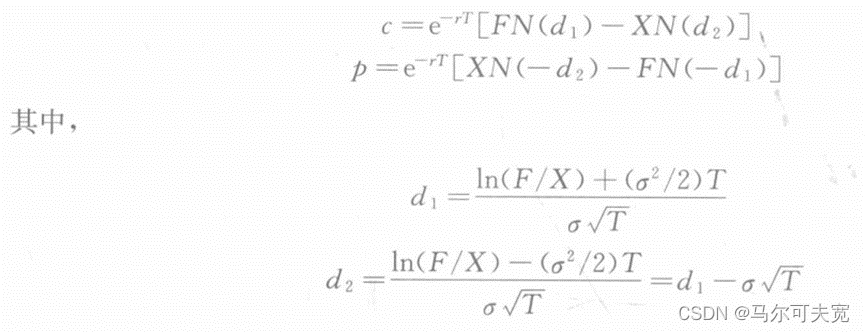
7.权利金计息的期货期权定价模型
Asay修改了权利金计息的Black76期货期权定价模型:
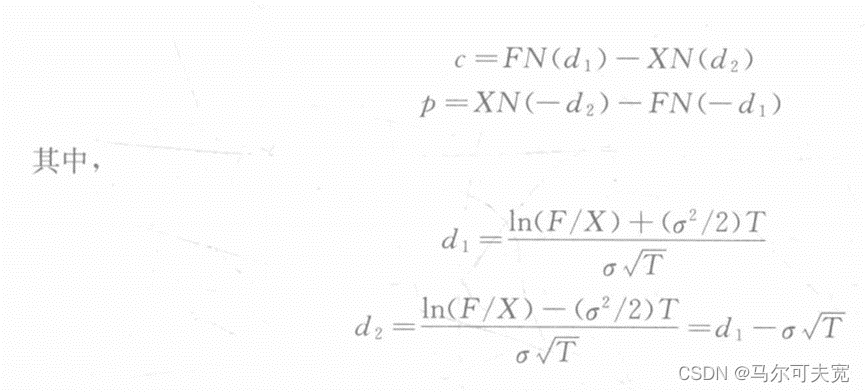
8.外汇期权定价模型
Garman和Kohlhagen修改了BS模型,使之可以用于欧式外汇期权的定价:
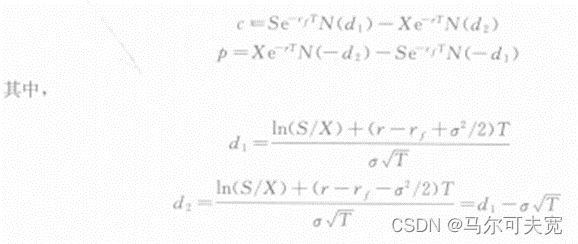
9.广义的BSM期权定价模型
如果引入一个持有成本率b,则BSM模型能够被一般化,这个模型可以用于定价标的为无股息股票、连续支付股息的股票、期货、外汇的欧式期权:
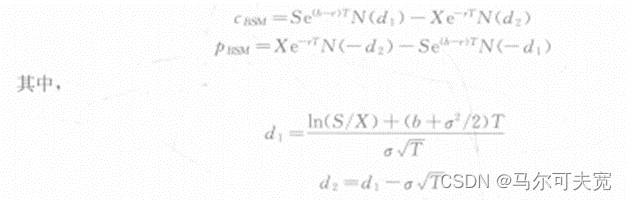
b=r时为1973年提出的无股息欧式期权定价模型;
b=r-q时为merton在1973年提出的连续股利欧式期权定价模型;
b=0时为black在1976年提出的期货期权定价模型;
b=0且r=0时为Asay在1982年提出的权利金计息下的期货期权定价模型;
b=r-rf时为外汇期权定价模型。
10.代码部分
import numpy as np
from scipy.stats import normclass BSM_Model:def __init__(self,S,K,T,sigma,r,b,opt):self.S=Sself.K=Kself.T=Tself.sigma=sigmaself.r=rself.b=bself.opt=optdef d1(self):return (np.log(self.S/self.K)+(self.b+self.sigma**2/2)*self.T)/(self.sigma*np.sqrt(self.T))def d2(self):return self.d1()-self.sigma*np.sqrt(self.T)def option_value(self):if self.opt=='call':value=self.S*np.exp((self.b-self.r)*self.T)*norm.cdf(self.d1())-self.K*np.exp(-self.r*self.T)*norm.cdf(self.d2())else:value = -self.S * np.exp((self.b - self.r) * self.T) * norm.cdf(-self.d1()) + self.K * np.exp(-self.r * self.T) * norm.cdf(-self.d2())return value例1:

结果为:欧式看涨期权价格为2.1333684449162007
if __name__=='__main__':#b=r时为1973年提出的无股息欧式期权定价模型# eg:S=60K=65T=0.25r=0.08sigma=0.3b=ropt='call'call=BSM_Model(S,K,T,sigma,r,b,opt).option_value()print('欧式看涨期权价格为%s'%(call))例2:

结果为:欧式看跌期权价格为2.4647876467558305
if __name__=='__main__':#b=r-q时为merton在1973年提出的连续股利欧式期权定价模型S=100K=95T=0.5r=0.1q=0.05sigma=0.2b=r-qopt='put'put=BSM_Model(S,K,T,sigma,r,b,opt).option_value()print('欧式看跌期权价格为%s'%(put))例3:

结果为:看跌期货期权价格为1.7010507252362679
if __name__=='__main__':#b=0时为black在1976年提出的期货期权定价模型F = 19K = 19T = 0.75r = 0.1sigma = 0.28b = 0opt = 'put'put = BSM_Model(F, K, T, sigma, r, b, opt).option_value()print('看跌期货期权价格为%s' % (put))例4:

结果为:看跌期货期权价格为65.61854211535751
if __name__=='__main__':#b=0且r=0时为Asay在1982年提出的权利金计息下的期货期权定价模型F = 4200K = 3800T = 0.75r =0sigma = 0.15b = 0opt = 'put'put = BSM_Model(F, K, T, sigma, r, b, opt).option_value()print('看跌期货期权价格为%s' % (put))例5:

结果为:看涨外汇权价格为0.02909925314943973
if __name__=='__main__':#b=r-rf时为外汇期权定价模型S = 1.56K = 1.6T = 0.5r = 0.06rf=0.08sigma = 0.12b = r-rfopt = 'call'call = BSM_Model(S, K, T, sigma, r, b, opt).option_value()print('看涨外汇权价格为%s' % (call))
相关文章:

期权定价模型系列【1】—BSM通用式模型
这是期权定价模型专栏的第一篇文章,此专栏旨在分享一些期权定价模型,将会从最基础的BSM模型开始写起,逐步扩散到蒙特卡洛模拟、二叉树等数值法模型,以及跳跃扩散模型、随机波动率模型,神经网络模型等等。 如果你觉得有…...
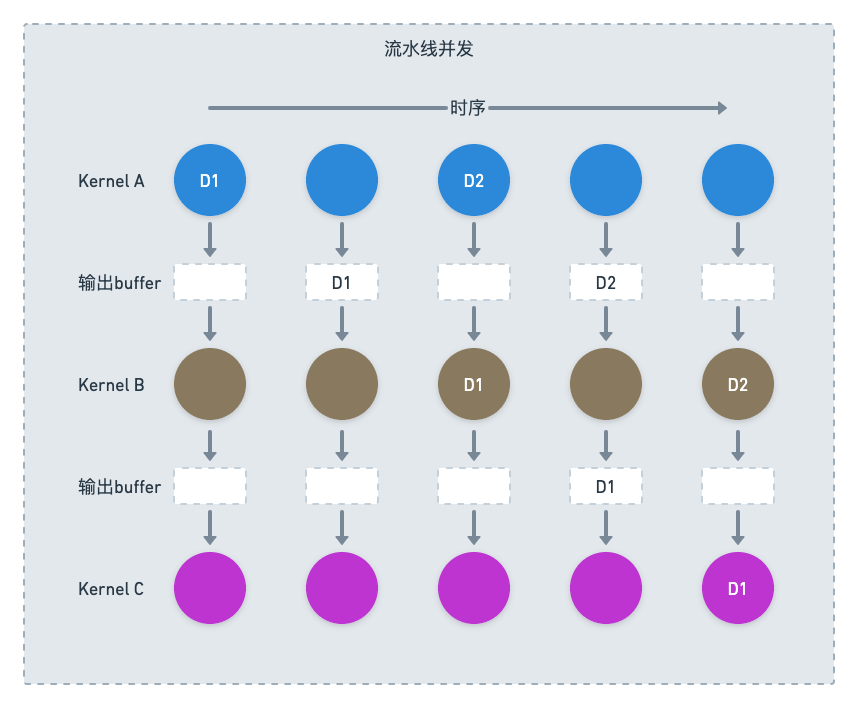
HA3 SQL样本实验:一种混合计算查询的全新样本解决方案
作者:陆唯一(芜霜) HA3(对外开源代号:Havenask )是阿里智能引擎团队自研的大规模分布式检索系统,广泛应用于阿里内部的搜索业务,是十多年来阿里在电商领域积累下来的核心竞争力产品。Ha3 SQL 是在原有Ha3引…...
)
Linux(Web与html)
域名 DNS与域名: 网络是基于tcp/ip协议进行通信和连接的 tcp/ip协议是五层协议:应用层–传输层—网络层----数据链路层----物理层每一台主机都有一个唯一的地址标识(固定的ip地址,用于区分用户和计算机。 ip地址:由…...
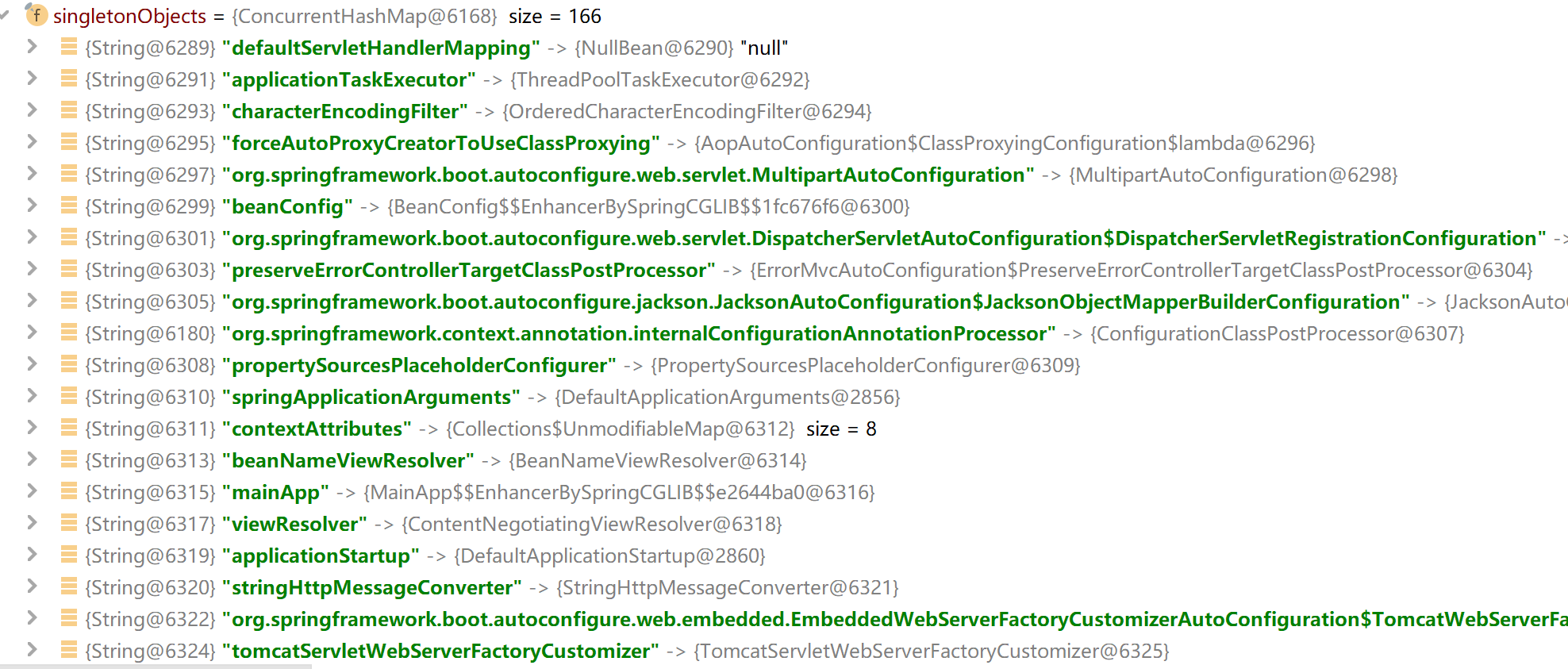
SpringBoot 底层机制分析[上]
文章目录 分析SpringBoot 底层机制【Tomcat 启动分析Spring 容器初始化Tomcat 如何关联Spring 容器】[上]搭建SpringBoot 底层机制开发环境Configuration Bean 会发生什么,并分析机制提出问题:SpringBoot 是怎么启动Tomcat ,并可以支持访问C…...
电源控制--对数与db分贝
在控制理论中,"db"通常表示分贝(decibel)的缩写。分贝是一种用于度量信号强度、增益或衰减的单位。 在控制系统中,分贝常用于描述信号的增益或衰减。通常,增益以正数的分贝值表示,而衰减以负数的…...
)
LeetCode 1749. 任意子数组和的绝对值的最大值(前缀和)
题目: 链接:LeetCode 1749. 任意子数组和的绝对值的最大值 难度:中等 给你一个整数数组 nums 。一个子数组 [numsl, numsl1, …, numsr-1, numsr] 的 和的绝对值 为 abs(numsl numsl1 … numsr-1 numsr) 。 请你找出 nums 中 和的绝对…...
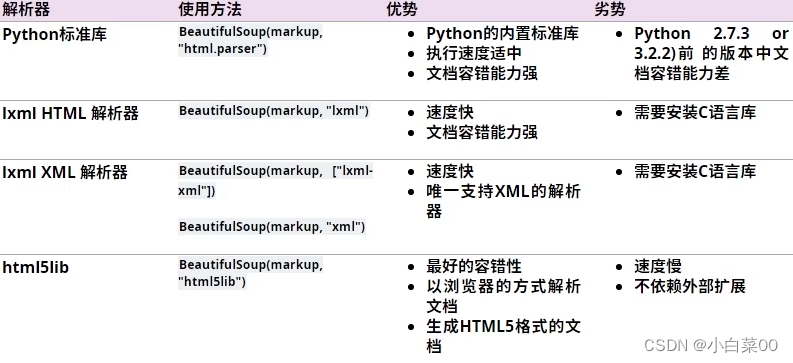
python爬虫相关
目录 初识爬虫 爬虫分类 网络爬虫原理 爬虫基本工作流程 搜索引擎获取新网站的url robots.txt HTHP协议 Resquests模块 前言: 安装 普通请求 会话请求 response的常用方法 简单案例 aiohttp模块 使用前安装模块 具体案例 数据解析 re解析 bs4…...
PAT(Advanced Level) Practice(with python)——1023 Have Fun with Numbers
Code N int(input()) D_N 2*N # print(Yes)if len(str(D_N))>len(str(N)):print(No) else:for s in str(D_N):if s not in str(N) or str(D_N).count(s)!str(N).count(s):print("No")breakelse:print(Yes) print(D_N)...

springboot vue 初步集成onlyoffice
文章目录 前言一、vue ts1. 安装依赖2. onlyoffice组件实现(待优化)3. 使用组件4. 我的配置文件 二、springboot 回调代码1. 本地存储 三、效果展示踩坑总结问题1问题2 前言 对接onlyoffice,实现文档的预览和在线编辑功能。 一、vue ts …...
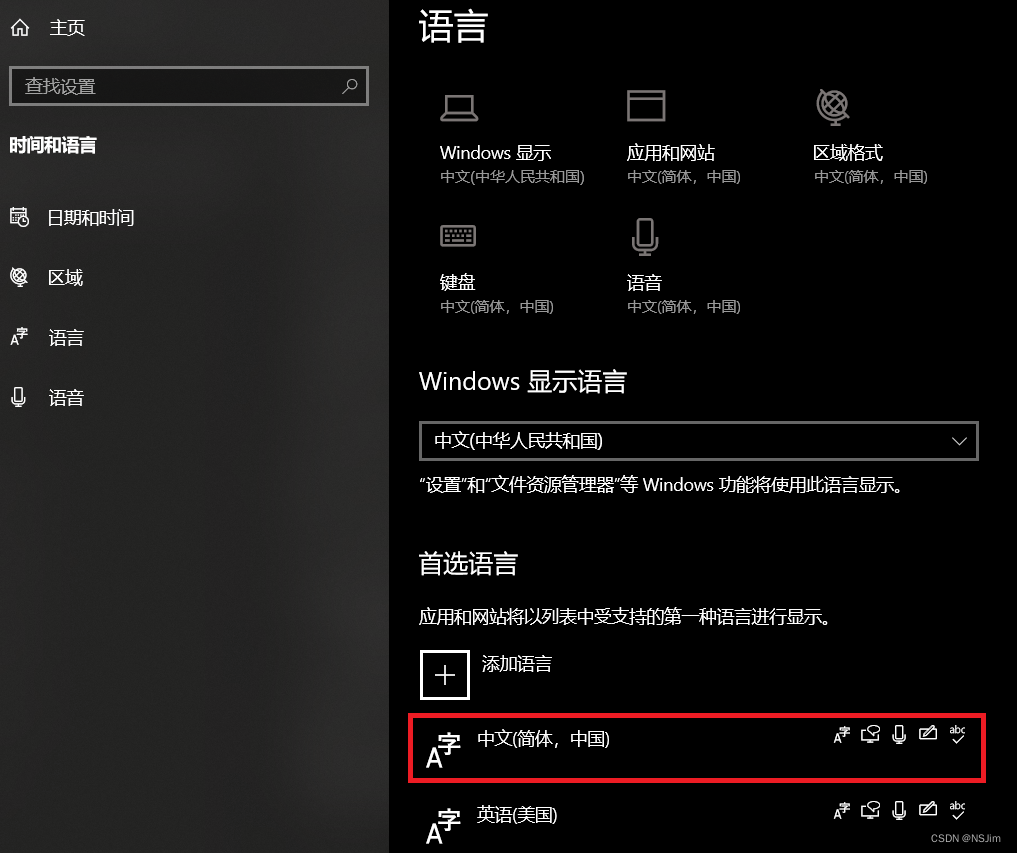
Win10语言设置 - 显示语言和应用语言
前言 Win10的语言设置可以设置显示语言和应用语言。其中,显示语言用于显示系统文字;应用语言用于应用程序显示文字。下文介绍如何设置。 显示语言 打开系统设置,选择时间和语言,如下图: 修改Windows显示语言即可更…...

RxJava的前世【RxJava系列之设计模式】
一. 前言 学习RxJava,少不了介绍它的设计模式。但我看大部分文章,都是先将其用法介绍一通,然后再结合其用法,讲解其设计模式。这样当然有很多好处,但我个人觉得,这种介绍方式,对于没有接触过Rx…...

sql 语句 字段字符串操作
substring_index() 函数 字符串截取 表达式:substring_index(column,str,count) 释义:截取字符串column,str出现从前往后数第count次,之前的所有字符 示例语句:SELECT substring_index(‘www.baidu.com’,‘.’,2) 结…...
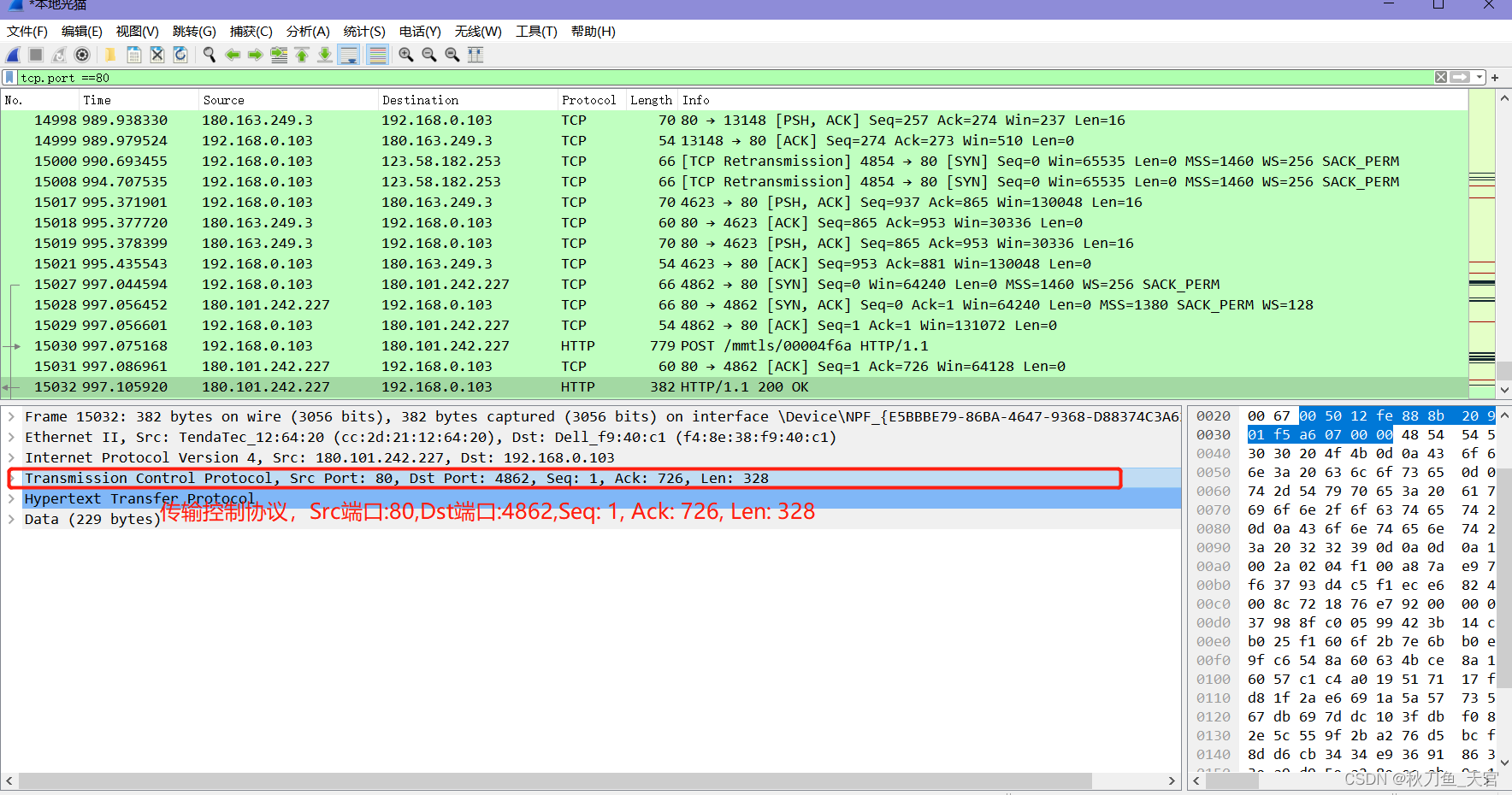
【网络工程】网络流量分析工具 Wireshark
文章目录 第一章:WireShark介绍第二章:WireShark应用第三章:Wireshark 实战 第一章:WireShark介绍 Wireshark (前身 Ethereal):它是一个强大的网络封包分析软件工具 ! 此工具使用WinPCAP作为接口,直接与网卡…...
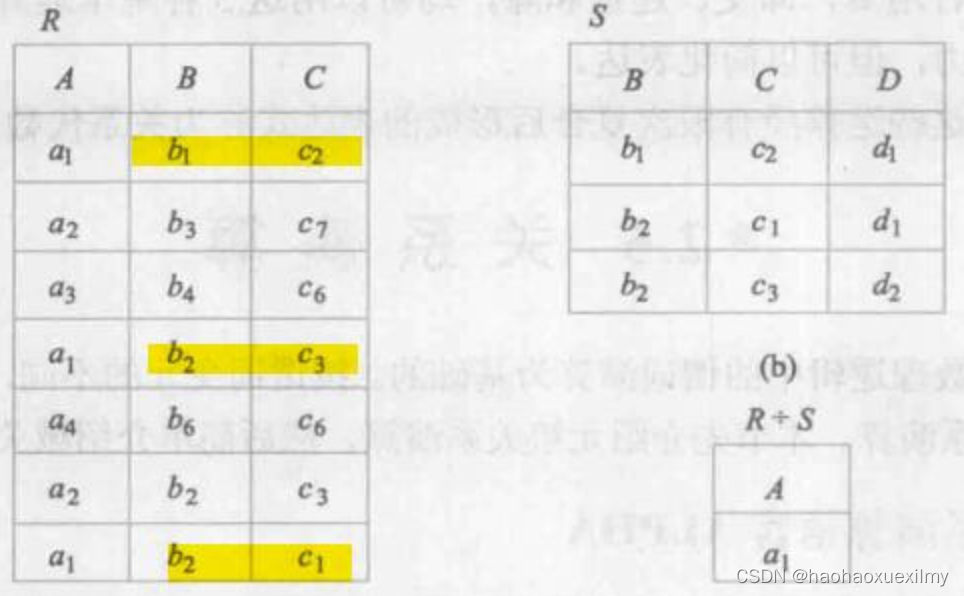
数据库总结
第一章绪论 一、数据库系统概述 1. 数据库的4个基本概念 1.数据:数据库中存储的基本对象,描述事物的符号记录。 2.数据库:长期储存在计算机内、有组织的、可共享的大量数据的集合。较小的冗余度、较高的数据独立性、易扩展性 3.数据库管…...

虹科方案 | 成都大运会进行时,保障大型活动无线电安全需要…
成都大运会 7月28日,备受关注的第31届世界大学生夏季运动会在成都正式开幕。据悉,这是全球首个5G加持的智慧大运会,也是众多成熟信息技术的综合“应用场”。使用基于5G三千兆、云网、8K超高清视频等技术,在比赛现场搭建多路8K摄像…...
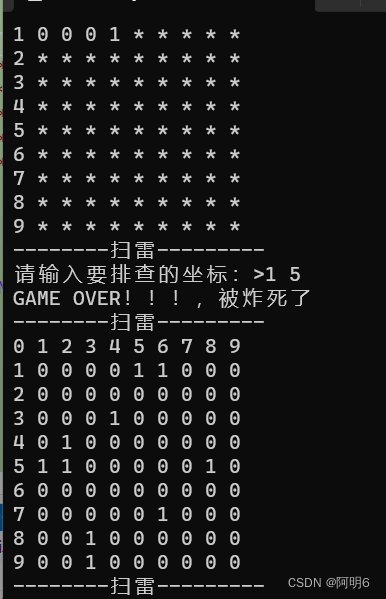
【C语言】扫雷 小游戏
文章目录 一、游戏规则二、 代码逻辑三、游戏实现1. 游戏菜单设计2.设计雷区并随机布置雷(1) 设置雷区(2) 布置雷 3.排查雷 四、源码 一、游戏规则 1. 在9*9的小格子中,任意选取一个坐标(格子),选择后发现,如果没点中雷…...

Jmeter(六) - 从入门到精通 - 建立数据库测试计划(详解教程)
1.简介 在实际工作中,我们经常会听到数据库的性能和稳定性等等,这些有时候也需要测试工程师去评估和测试,因此这篇文章主要介绍了jmeter连接和创建数据库测试计划的过程,在文中通过示例和代码非常详细地介绍给大家,希望对各位小伙…...
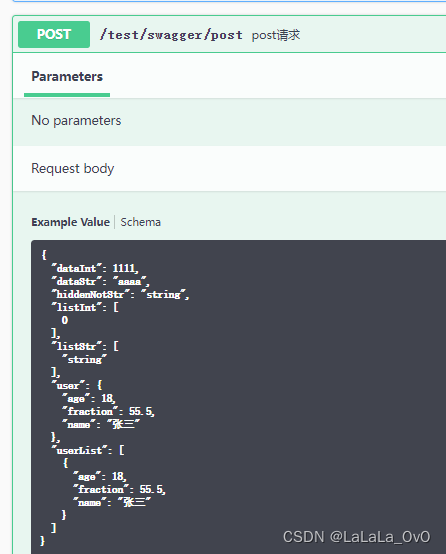
swagger 3.0 学习笔记
引入pom <dependency><groupId>io.springfox</groupId><artifactId>springfox-boot-starter</artifactId><version>3.0.0</version></dependency>配置 import io.swagger.models.auth.In; import io.swagger.v3.oas.annotati…...

07 |「异步任务」
前言 实践是最好的学习方式,技术也如此。 文章目录 前言一、进程与线程1、进程2、线程 二、实现 一、进程与线程 1、进程 进程(Process)是操作系统分配资源的基本单位,它是一个执行中的程序实例;每个进程都有自己独立的内存空间,不同进程的内存是相互独…...

LoRaWan网关设计之入门指南
快速开始 以下是在目标平台本身上构建和运行 LoRaWan网关 的三步快速入门指南。 第 1 步:克隆 网关源码库 git clone https://github.com/lorabasics/basicstation.git...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
