Codeforces Round 889 (Div. 2)C题题解
文章目录
- [Dual (Hard Version)](https://codeforces.com/contest/1855/problem/C2)
- 问题建模
- 问题分析
- 1.按元素值分类讨论,正负不同时存在时
- 2.若正负同时存在时
- 代码
Dual (Hard Version)

问题建模
给定n个数,n不超过20,且每个数ai, − 20 < = a i < = 20 -20<=ai<=20 −20<=ai<=20,可以执行多次操作,每次可以选择两个数ai,aj,使得ai=ai+aj,需要在31次操作内使得元素为非降序排列,并输出操作数和操作使选取的i,j。
问题分析
1.按元素值分类讨论,正负不同时存在时
若元素值都为大于等于0时,对于每一个比前一个元素小的元素,加上前面元素后,就会变成所需的大小关系,操作最多为19次。
若元素值都为小于等于0时,对于每一个比前一个元素小的元素,让前面的元素加上当前元素即可变成所需的大小关系,操作最多为19次。
2.若正负同时存在时
若正负数都有,则可以将负数变成正的或者正数变为负的,变为上面两种情况之一,由于转换为上面两种情况后最多需要19次操作才能使得最终元素排列为所需,则最多有12次操作可以将当前情况变为上述两种情况之一。
由于改变元素正负需要通过最大正数或者负数来进行,则从绝对值最大的正负性的情况来分析。
若绝对值最大的数为正数,则考虑将负数都变为正数,若负数的个数不超过12时,可以完成。
若超过12个则只能考虑将正数都变为负数,由于负数个数超过12,则正数最多只有7个数,则可以考虑使用5次操作获得一个比所有正数绝对值大的负数,然后再将7个正数变为负数,由于i,j选择同一个数时,等价2乘该数,则选择5次有2^5,负数绝对值最小的数为-1,5次操作后为-32其绝对值大于最大的正数,故可以在12次内将将正数变为负数。(绝对值最大为负数同理)
所以最终有解的情况,为取将所有元素变为大于等于0的数所需操作以及将所有元素变为小于等于0的数所需操作的最小操作数的操作方案。
代码
#include<bits/stdc++.h>#define x first
#define y second
#define C(i) str[0][i]!=str[1][i]
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
const int N = 30, Mod = 998244353, P = 2048;
int a[N];void solve() {int n;cin >>n;///正负数个数,以及正负数中绝对值最大的元素的下标,起始时对应元素为0int pcnt=0,ncnt=0,minp=0,maxp=0;for(int i=1;i<=n;i++){cin >>a[i];if(a[i]>0){pcnt++;if(a[i]>a[maxp]) maxp=i;}else if(a[i]<0){ncnt++;if(abs(a[i])>abs(a[minp])) minp=i;}}if(pcnt==0&&ncnt==0){cout <<0<<endl;}else {int x1=0,y1=0;///记录,获得正数绝对值最大,和负数绝对值最大所需的操作数if(abs(a[maxp])>=abs(a[minp])) y1=5;else x1=5;//采用变正和变负中操作数最小的操作方案if(x1+ncnt<=y1+pcnt){cout <<x1+ncnt+n-1<<"\n";for(int i=0;i<x1;i++) cout <<maxp<<" " <<maxp<<"\n";for(int i=1;i<=n;i++){if(a[i]<0) cout <<i <<" " <<maxp <<"\n";}for(int i=1;i<n;i++) cout <<i+1 <<" " <<i <<"\n";}else{cout <<y1+pcnt+n-1 <<"\n";for(int i=0;i<y1;i++) cout <<minp<<" " <<minp<<"\n";for(int i=1;i<=n;i++){if(a[i]>0) cout <<i <<" " <<minp <<"\n";}for(int i=n;i>1;i--) cout <<i-1 <<" " <<i <<"\n";}}
}int main() {int t = 1;cin >> t;while (t--) solve();return 0;
}
相关文章:

Codeforces Round 889 (Div. 2)C题题解
文章目录 [Dual (Hard Version)](https://codeforces.com/contest/1855/problem/C2)问题建模问题分析1.按元素值分类讨论,正负不同时存在时2.若正负同时存在时代码 Dual (Hard Version) 问题建模 给定n个数,n不超过20,且每个数ai,…...

无涯教程-Perl - Subroutines(子例程)
定义子程序 Perl编程语言中 Subroutine子程序定义的一般形式如下: sub subroutine_name {body of the subroutine } 调用该Perl Subroutine的典型方式如下- subroutine_name( list of arguments ); 在Perl 5.0之前的版本中,调用 Subroutine的语法略有不同&…...
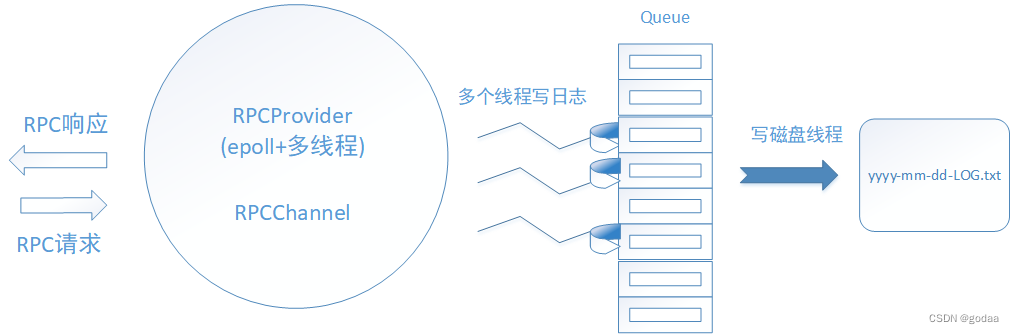
Rpc异步日志模块
Rpc异步日志模块作用 在一个大型分布式系统中,任何部署的分布式节点都可能发生崩溃,试想如果用普通的办法,即先排查哪个节点down掉了,找到down掉的节点后采取调试工具gdb调试该节点,进而排查宕机的原因。这中排查方法…...

python-pip
pip 路径 python 下载后自带pip ,在scripts 下,如 D:\install\python\Scripts numpy pip3 install numpy scipy matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simplepandas D:\install\python\Scripts>pip3 install pandas -i https://pypi.tuna.tsingh…...

无涯教程-Perl - getppid函数
描述 该函数返回父进程的进程ID。 语法 以下是此函数的简单语法- getppid返回值 该函数返回父进程的进程ID。 例 以下是显示其基本用法的示例代码- #!/usr/bin/perl$ppidgetppid();print "Parent Process ID $ppid\n";执行上述代码后,将产生以下输出- Paren…...
1.2 汽车电子控制系统的基本构成)
AUTOSAR规范与ECU软件开发(基础篇)1.2 汽车电子控制系统的基本构成
目录 前言 1、 传感器 2、 电子控制单元(ECU) 3、 执行器 前言 汽车电子控制系统主要由传感器(Sensor) 、 电子控制单元(Electronic Control Unit, ECU) 和执行器(Actuator) 组成(图1.1) ,对被控对象(Controlled Object)...
)
一个可以通过多个条件筛选的系统界面是如何实现的(springboot+mybatis)
比如我们有一个订单记录管理界面 条件可以通过订单号、商品名称、创建日期范围、价格范围。。。来进行筛选查询。 首先我们先确定数据库订单表(我这里就不做连表了,都放在一个表中)模拟一个订单表 order表 订单号商品名称创建日期价格地址…...
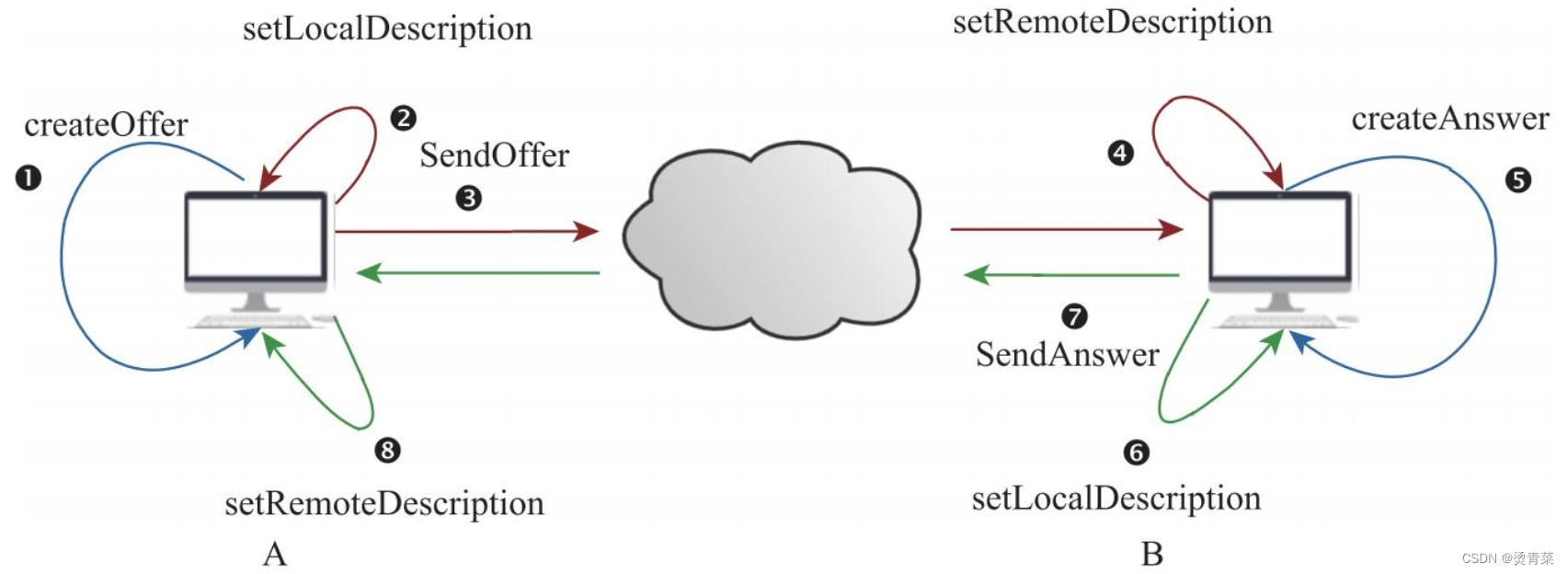
WebRTC | 实现数据流的一对一通信
目录 一、浏览器对WebRTC的支持 二、MediaStream与MediaStreamTrack 三、RTCPeerConnection 1. RTCPeerConnection与本地音视频数据绑定 2. 媒体协商SDP 3. ICE (1)Candidate信息 (2)WebRTC收集Candidate (3&…...
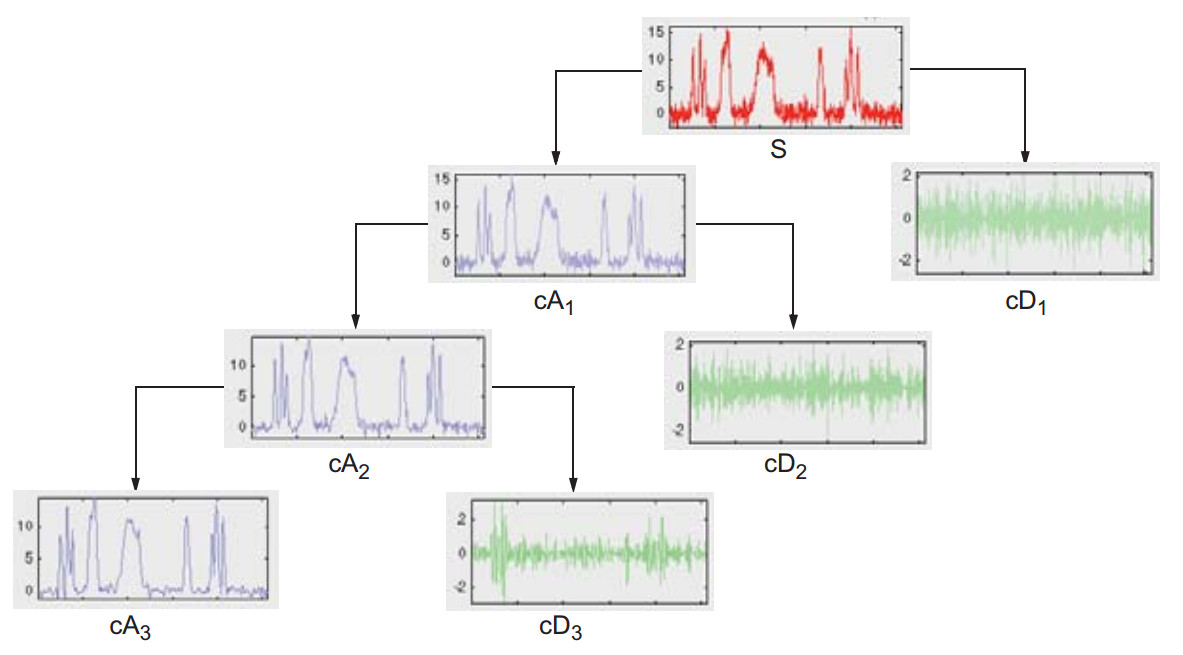
基于MATLAB小波变换的信号突变点检测
之前在不经意间也有接触过求突变点的问题。在我看来,与其说是求突变点,不如说是我们常常玩的"找不同"。给你两幅图像,让你找出两个图像中不同的地方,我认为这其实也是找突变点在生活中的应用之一吧。回到找突变点位置上…...
JUC并发编程(JUC核心类、TimeUnit类、原子操作类、CASAQS)附带相关面试题
目录 1.JUC并发编程的核心类 2.TimeUnit(时间单元) 3.原子操作类 4.CAS 、AQS机制 1.JUC并发编程的核心类 虽然java中的多线程有效的提升了程序的效率,但是也引发了一系列可能发生的问题,比如死锁,公平性、资源管理…...
个人用C#编写的壁纸管理器 - 开源研究系列文章
今天介绍一下笔者自己用C#开发的一个小工具软件:壁纸管理器。 开发这个小工具的初衷是因为Windows操作系统提供的功能个人不满意,而且现在闲着,所以就随意写了个代码。如果对读者有借鉴参考作用就更好了,能够直接代码段复用即可。…...

iTextSharp 生成PDF
示例代码定义了一个名为PdfController的API控制器,其中的GeneratePdf方法创建了一个新的PDF文档,并将内容添加到文档中。最后,将文档内容转换为字节数组,并通过File方法返回给前端。 注意,你需要在你的项目中添加对iT…...
基于微信小程序的传染病酒店隔离平台设计与实现(Java+spring boot+MySQL+微信小程序)
获取源码或者论文请私信博主 演示视频: 基于微信小程序的传染病酒店隔离平台设计与实现(Javaspring bootMySQL微信小程序) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:…...

vue3中用watch监听响应式数据的注意点
如果你在vue3中使用reactive()方法创建响应式数据,然后又用torefs()方法将响应式数据解构成单一的ref响应式数据。 此时,如果你想用watch监听解构出来单一的响应式数据,watch不起作用。 此时,你需要用watch监听之前的reactive()…...

Jmeter(五) - 从入门到精通 - 创建网络计划实战和创建高级Web测试计划(详解教程)
1.简介 上一篇中已经将其的理论知识介绍了一下,这一篇就带着大家一步一步的把上一篇介绍的理论知识实践一下,然后再说一下如何创建高级web测试计划。 2.网络计划实战 通过上一篇的学习,将其分类为: (1)不需…...

【单片机】51单片机,TLC2543,驱动程序,读取adc
TLC2543 是一款 12 位精密模数转换器 (ADC)。 1~9、11、12——AIN0~AIN10为模拟输入端; 15——CS 为片选端; 17——DIN 为串行数据输入端;(控制字输入端,用于选择转换及输出数据格式) 16——…...

誉天HCIE-Cloud_Computing3.0课程简介
课时:60 第一天 1. 华为云 Stack 解决方案及架构介绍 3. 华为云 Stack 的安装流程解析及规划设计 4. 华为云 Stack 的网络平面的规划解析 5. 华为云 Stack Deploy 部署工具的安装,配置,创建工程,下载 LLD 表 6. 华为云 Stack 的 …...
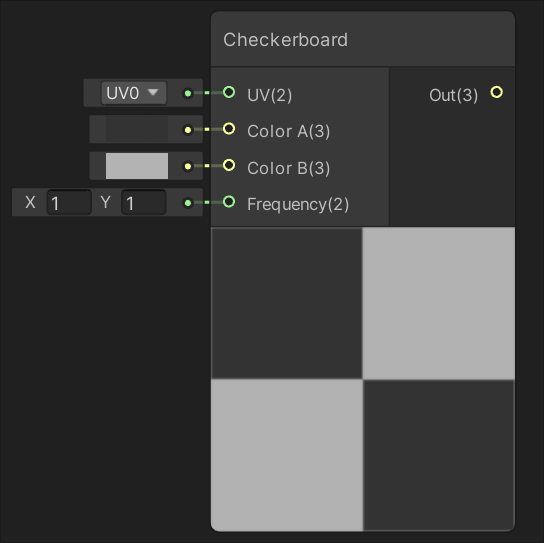
Unity之ShaderGraph 节点介绍 Procedural节点
程序化 噪声Gradient Noise(渐变或柏林噪声)Simple Noise(简单噪声)Voronoi(Voronoi 噪声) 形状Ellipse(椭圆形)Polygon(正多边形)Rectangle(矩形…...

期权定价模型系列【1】—BSM通用式模型
这是期权定价模型专栏的第一篇文章,此专栏旨在分享一些期权定价模型,将会从最基础的BSM模型开始写起,逐步扩散到蒙特卡洛模拟、二叉树等数值法模型,以及跳跃扩散模型、随机波动率模型,神经网络模型等等。 如果你觉得有…...
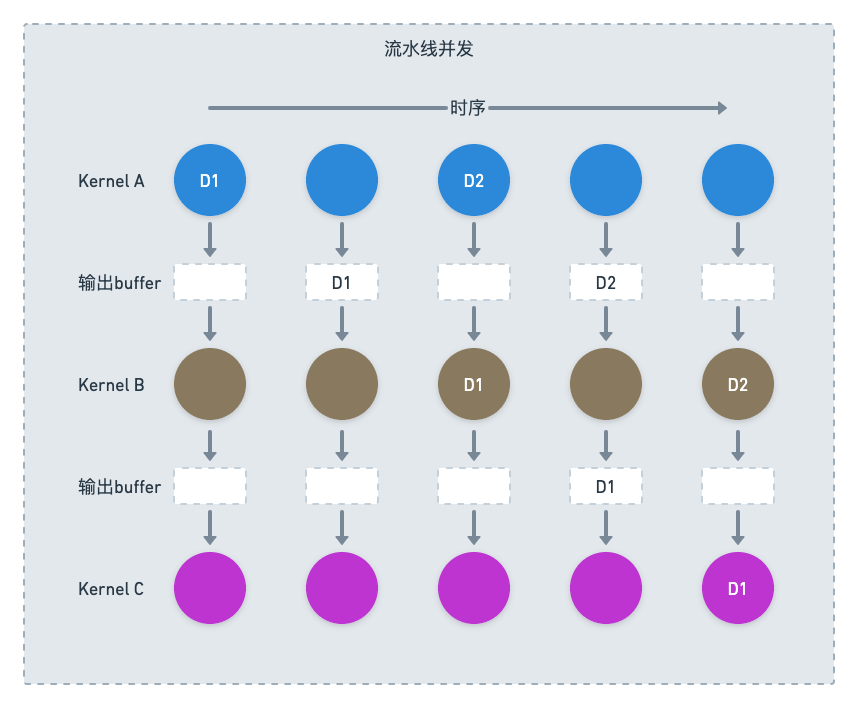
HA3 SQL样本实验:一种混合计算查询的全新样本解决方案
作者:陆唯一(芜霜) HA3(对外开源代号:Havenask )是阿里智能引擎团队自研的大规模分布式检索系统,广泛应用于阿里内部的搜索业务,是十多年来阿里在电商领域积累下来的核心竞争力产品。Ha3 SQL 是在原有Ha3引…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
