Leetcode-每日一题【剑指 Offer 14- I. 剪绳子】
题目
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
2 <= n <= 58
解题思路
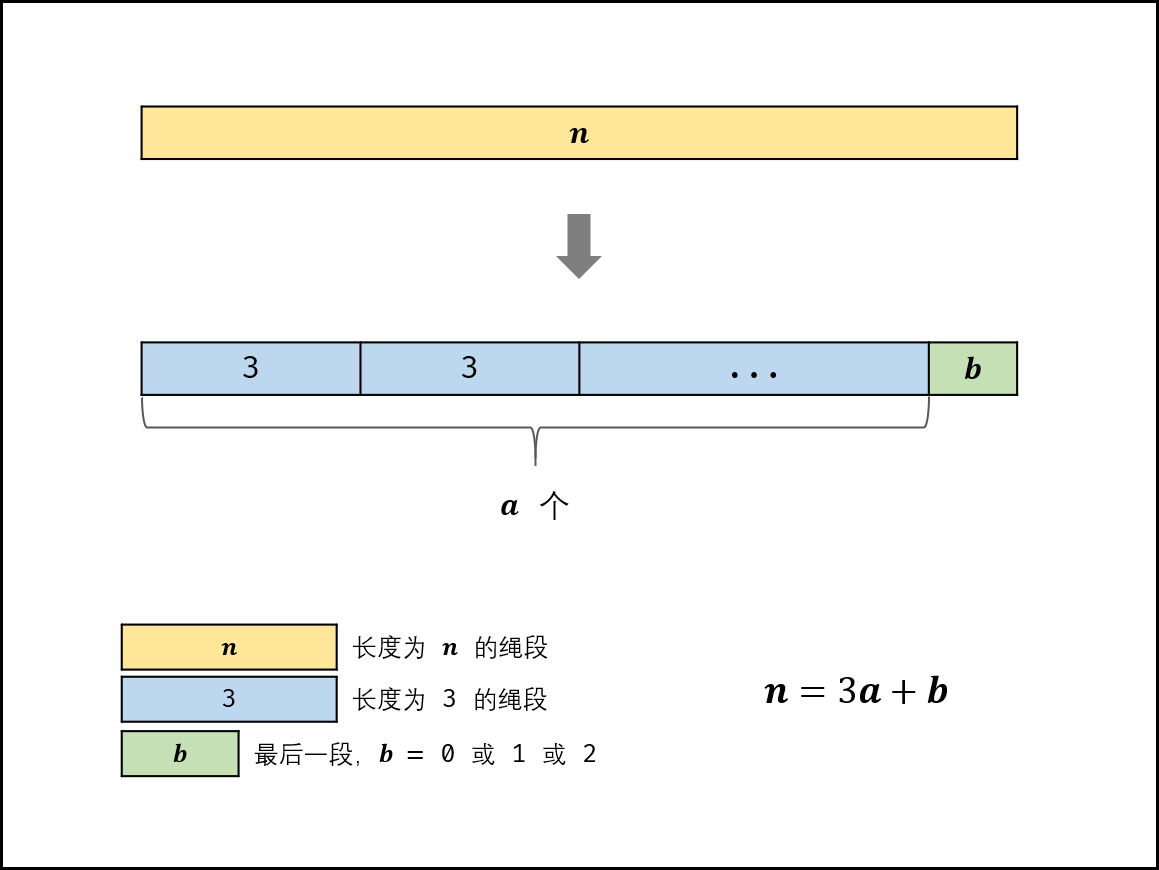
1.题目要求我们将绳子剪切为乘积最大的 m 段,这其中蕴含着一个数学问题,就是当我们尽可能将绳子以长度 3等分为多段时,乘积最大。这个推论大家可以自己去证明一下。
2.有了这个推论,这个问题就轻而易举了,
①切分规则:
最优: 3 。把绳子尽可能切为多个长度为 3 的片段,留下的最后一段绳子的长度可能为 0,1,2 三种情况。
次优: 2。若最后一段绳子长度为 2 ;则保留,不再拆为 1+1 。
最差: 1。若最后一段绳子长度为 1 ;则应把一份 3+1 替换为 2+2,因为 2×2>3×1
②算法流程:
- 当 n≤3 时,按照规则应不切分,但由于题目要求必须剪成 m>1 段,因此必须剪出一段长度为 1 的绳子,即返回 n−1 。
- 当 n>3 时,求 n 除以 3 的 整数部分 res 和 余数部分 mod (即 n=3res+ mod =),并分为以下三种情况:
①当 b=0 时,直接返回 3^a;
②当 b=1 时,要将一个 1+3 转换为 2+2,因此返回 3^{a-1} *4
③当 b=2 时,返回 3^a*2
代码实现
class Solution {public int cuttingRope(int n) {if(n <= 2){return 1;}if(n == 3){return 2;}int res = n / 3;int mod = n % 3;if(mod == 0){return pow(3,res);}else if(mod == 1){return pow(3,res - 1) * 4;}else {return pow(3,res) * 2;}}int pow(int i, int k){int sum = 1;for(i = 1; i <= k; i++){sum = sum * 3;}return sum;}}测试结果
相关文章:

Leetcode-每日一题【剑指 Offer 14- I. 剪绳子】
题目 给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少?例如࿰…...

【图论】单源最短路问题
Dijkstra算法 -- 这是我职业生涯中唯一一个会写,却叫不上名字的算法 Dijkstra算法是一种单源最短路径算法,用于找出图中从一个源点到其他所有点的最短路径。该算法的原理是采用贪心策略,每次将距离源点最近的点加入到已确定最短路径的集合中…...
物理层扩展以太网
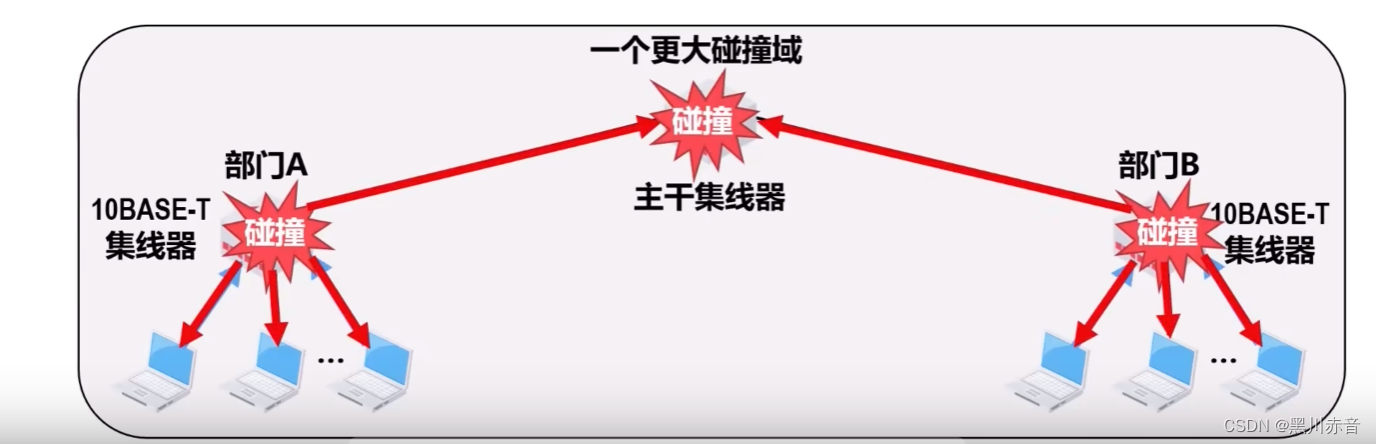
扩展站点与集线器之间的距离: 在10BASE-T星型以太网中,可使用光纤和一对光纤调制解调器来扩展站点与集线器之间的距离。 为站点和集线器各增加一个用于电信号和光信息号转换的光纤调制解调器,以及他们之间的通信光纤。 扩展共享式以太…...
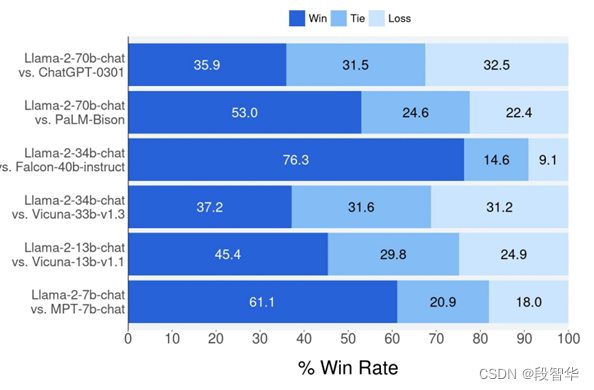
Llama 2 with langchain项目详解(一)
Llama 2 with langchain项目详解(一) 2023年2月25日,美国Meta公司发布了Llama 1开源大模型。随后,于2023年7月18日,Meta公司发布了Llama 2开源大模型,该系列包括了70亿、130亿和700亿等不同参数规模的模型。相较于Llama 1,Llama 2的训练数据增加了40%,上下文长度提升至…...
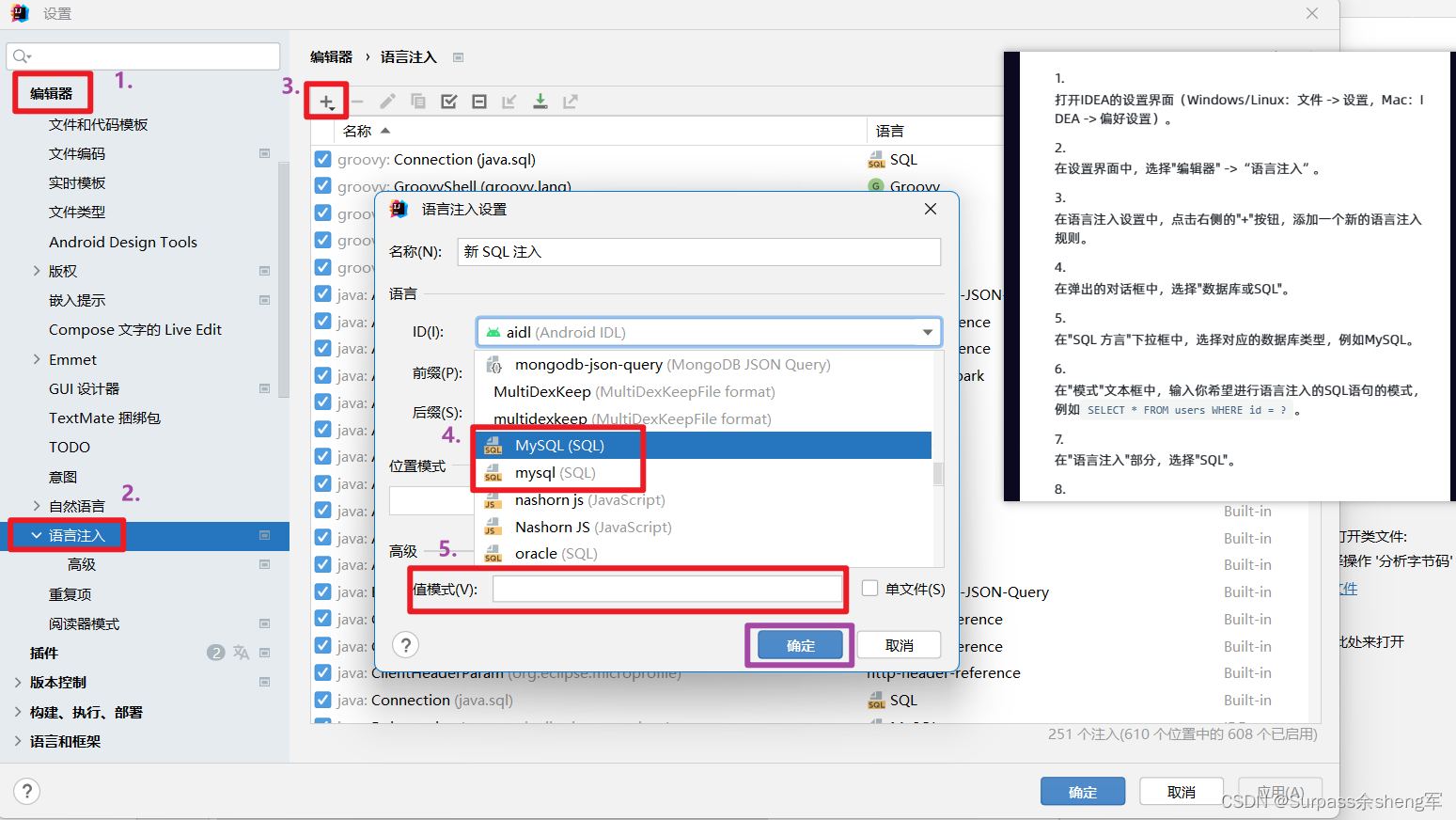
IDEA全局设置MyBatis中写SQL语句提示
把这两个设置改成MySQL即可:...

Linux 内存管理
顾名思义,Liunx内存管理子系统在系统中负责管理内存。它包括虚拟内存管理、段与页的实现、内核态与用户空的空间分配、将文件映射到进程空间等,很多很多酷炫的功能。 Linux内存管理是一个非常复杂的系统,它有非常多的可配置项。大部份这些配置…...

oracle怎样给某个普通用户授予杀自己用户会话的权限
一 问题描述 想给某个普通用户授予杀掉自己会话的权限 二 解决办法 2.1 用sys用户创建杀会话的存储过程 create or replace procedure scott_p_kill_session( v_sid number, v_serial number )asv_varchar2 varchar2(100);beginif v_sid is not null and v_serial is not n…...

redis的主从复制,哨兵和cluster集群
目录 一、redis的高可用 1)redis高可用的概念 2)Redis的高可用技术 二、redis主从复制 1)主从复制的作用 2)主从复制流程 三、redis一主二从的部署 实验组件 实验步骤 环境准备 修改内核参数 安装 Redis 创建redis工…...
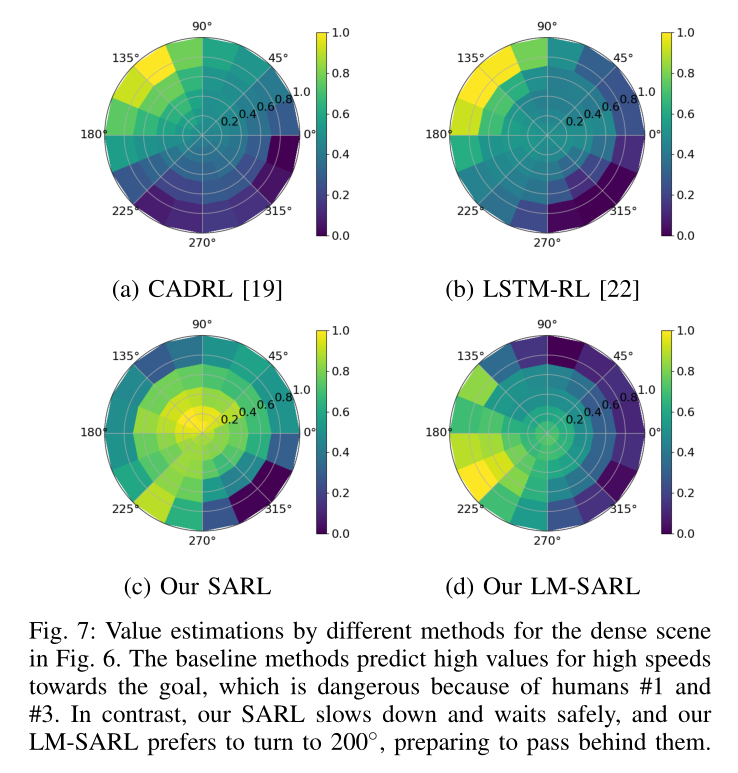
Crowd-Robot Interaction 论文阅读
论文信息 题目:Crowd-Robot Interaction:Crowd-aware Robot Navigation with Attention-based Deep Reinforcement Learning 作者:Changan Chen, Y uejiang Liu 代码地址:https://github.com/vita-epfl/CrowdNav 来源:arXiv 时间…...

什么是LIMS系统,LIMS实验室管理系统
LIMS是实验室信息管理系统,全称是Laboratory Information Management System,是将以数据库为核心的信息化技术与实验室管理需求相结合的信息化管理工具。它是由计算机硬件和应用软件组成,能够完成实验室数据和信息的收集、分析、报告和管理&a…...
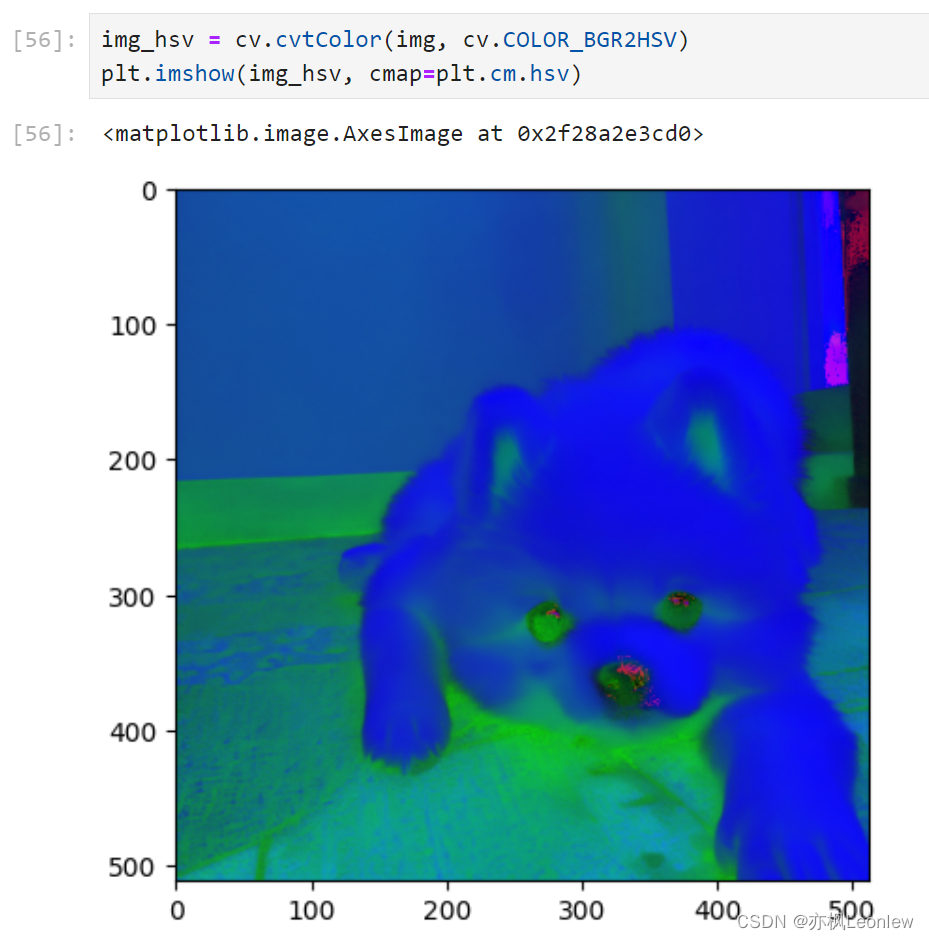
Python Opencv实践 - 图像属性相关
import numpy as np import cv2 as cv import matplotlib.pyplot as pltimg cv.imread("../SampleImages/pomeranian.png", cv.IMREAD_COLOR) plt.imshow(img[:,:,::-1])#像素操作 pixel img[320,370] print(pixel)#只获取蓝色通道的值 pixel_blue img[320,370,0]…...

PCB制造中铜厚度的重要性
电子产品中的PCB是现代电子设备中不可或缺的一部分。在PCB制造过程中,铜厚度是一个非常重要的因素。正确的铜厚度可以保证电路板的质量和性能,同时也影响着电子产品的可靠性和稳定性。 一般我们常见的铜厚有17.5um(0.5oz)&#x…...
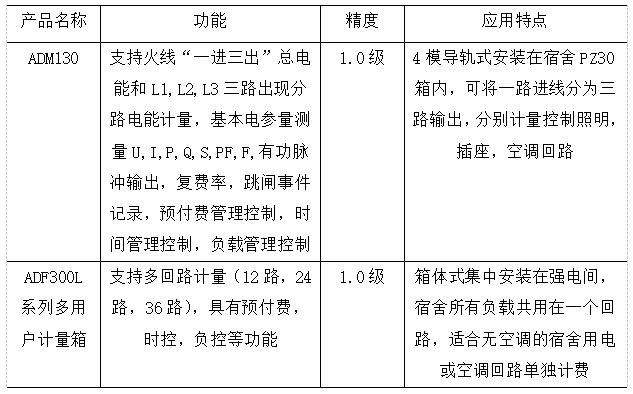
浅谈高校宿舍水电表远程智能管理的研究与应用
安科瑞 华楠 摘要:本系统的设计是基于485总线技术与TCP/IP网络技术相结合的方式来实现的,充分考虑了目前高校后勤水电表管理控制的实际情况,以传输可靠性高、技术成熟、成本低的485总线技术为基础,并与应用广泛的TCP/IP网络相结合…...
无货源跨境电商购物平台快速搭建(微商城、小程序、APP、网站)
无货源跨境电商购物平台的快速搭建可以通过以下步骤完成,并且可以同时开发微商城、小程序、APP和网站以满足不同用户的需求。 第一步:需求分析 在搭建之前,需要对平台的需求进行详细的分析。包括用户需求、功能需求、技术需求等等。这一步是…...
)
力扣:57. 插入区间(Python3)
题目: 给你一个 无重叠的 ,按照区间起始端点排序的区间列表。 在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。 来源:力扣(LeetC…...
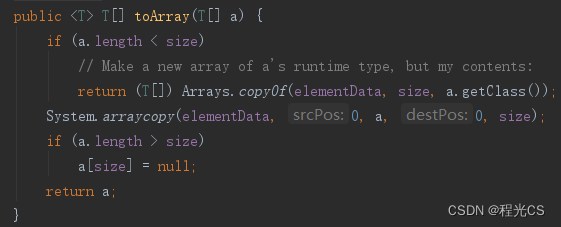
List和数组互转方法以及踩坑点
一、数组转List 1. 使用for循环逐个添加 String[] array {"A", "B", "C"}; List<String> list new ArrayList<>(); for (String element : array) {list.add(element); }2. 使用Arrays.asList(arr) String[] array {"A&q…...

css3背景渐变
1.线性渐变 <style>.box {width: 200px;height: 200px;border: 1px solid black;float: left;margin-left: 50px;}.box1 {background-image: linear-gradient(green, yellow, red);}/* 右上 */.box2 {background-image: linear-gradient(to right top, green, yellow, re…...
windows 安装免费3用户ccproxy ubuntu 代理上网
Windows 上进行安装 ubuntu 上进行设置 方法一 (临时的手段) 如果仅仅是暂时需要通过http代理使用apt-get,您可以使用这种方式。 在使用apt-get之前,在终端中输入以下命令(根据您的实际情况替换yourproxyaddress和proxyport)。 终…...

B树的插入与删除过程
B树的插入 原树: 插入key后,若导致原节点关键字数超过上限,则从中间位置( ⌈ m 2 ⌉ \lceil\frac{m}{2}\rceil ⌈2m⌉)将关键字分成两部分,左部分包含的关键字放在原节点中,右部分包含的关键…...
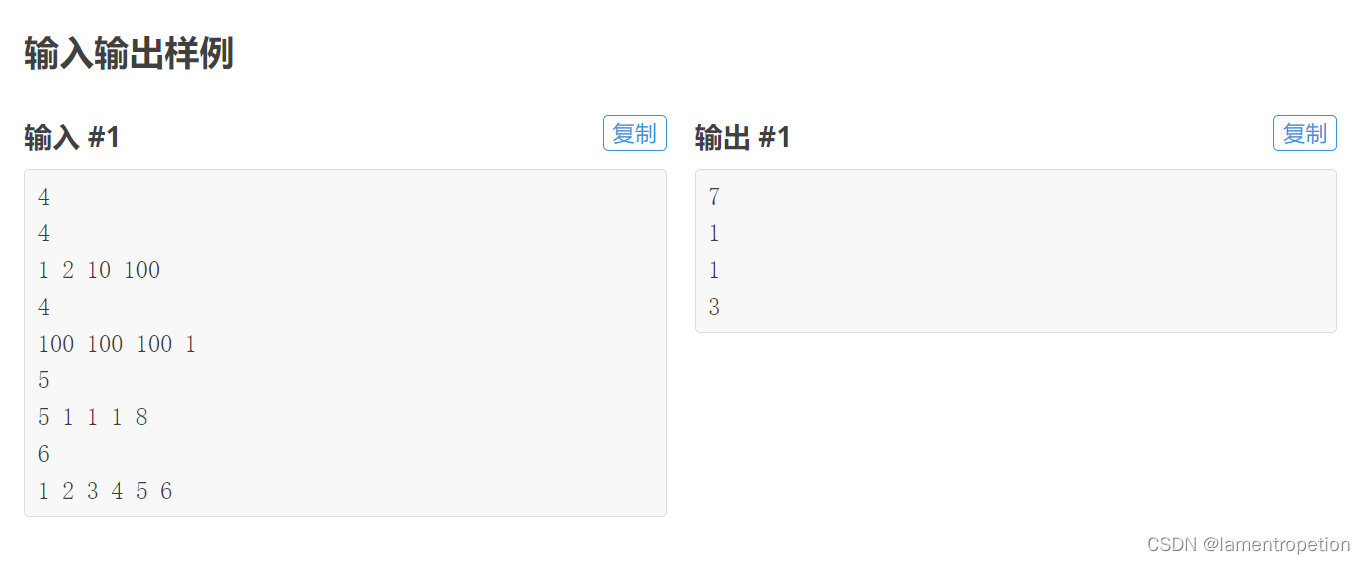
【二分】CF1623 C
Problem - 1623C - Codeforces 题意: 思路: 肯定是二分,我们去二分最小值,然后check的时候最小值要大于mid check的时候要让最小值尽可能大 注意到我们不需要去管最大值,只需要最小值尽可能大就好了,因…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...