[保研/考研机试] KY187 二进制数 北京邮电大学复试上机题 C++实现
描述
大家都知道,数据在计算机里中存储是以二进制的形式存储的。 有一天,小明学了C语言之后,他想知道一个类型为unsigned int 类型的数字,存储在计算机中的二进制串是什么样子的。 你能帮帮小明吗?并且,小明不想要二进制串中前面的没有意义的0串,即要去掉前导0。
输入描述:
多行,每一行表示要求的数字
输出描述:
输出共T行。每行输出求得的二进制串。
示例1
输入:
23
535
2624
56275
989835
输出:
10111
1000010111
101001000000
1101101111010011
11110001101010001011
思路:

源代码:
#include<iostream>
using namespace std;//例题6.1 二进制数
int main()
{int num;//针对多个输入的情况,只要还有输入,循环就一直进行while (cin >> num) {string s; //用于保存每次相除的余数while (num != 0) {s += (char)(num % 2 + '0'); //将每次num对2取模的余数转换成字符类型,并保存到s中num /= 2; //将num除以2}//考虑到测试用例中部分数值最终结果太长,用整型难以存储,直接将字符串s逆序输出即可for (int i = s.size() - 1; i >= 0; i--) {cout << s[i];}cout << endl;}return 0;
}
提交结果:

相关文章:

[保研/考研机试] KY187 二进制数 北京邮电大学复试上机题 C++实现
描述 大家都知道,数据在计算机里中存储是以二进制的形式存储的。 有一天,小明学了C语言之后,他想知道一个类型为unsigned int 类型的数字,存储在计算机中的二进制串是什么样子的。 你能帮帮小明吗?并且,小…...
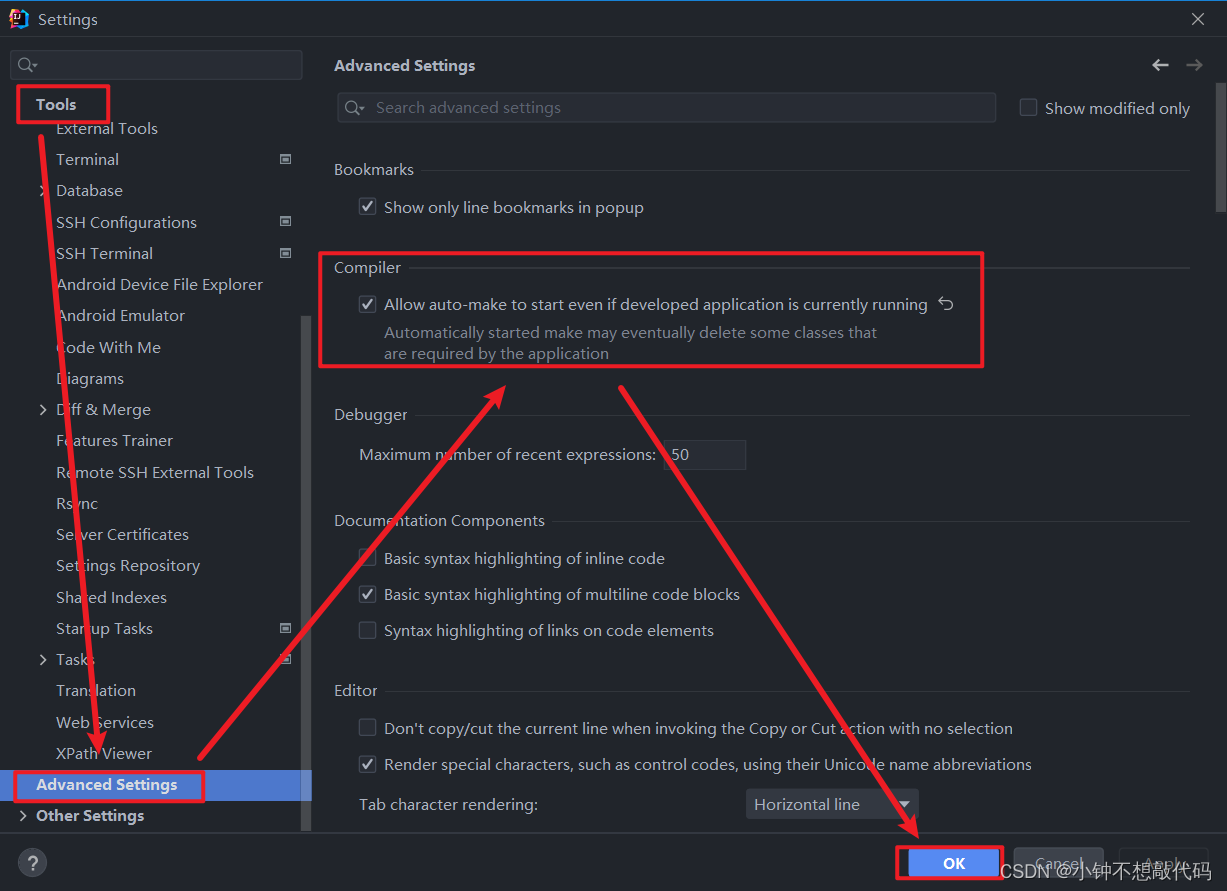
SpringBoot 热部署
一、启动热部署 1.1 开启开发者工具 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-devtools</artifactId><scope>runtime</scope><optional>true</optional> </dependency>…...
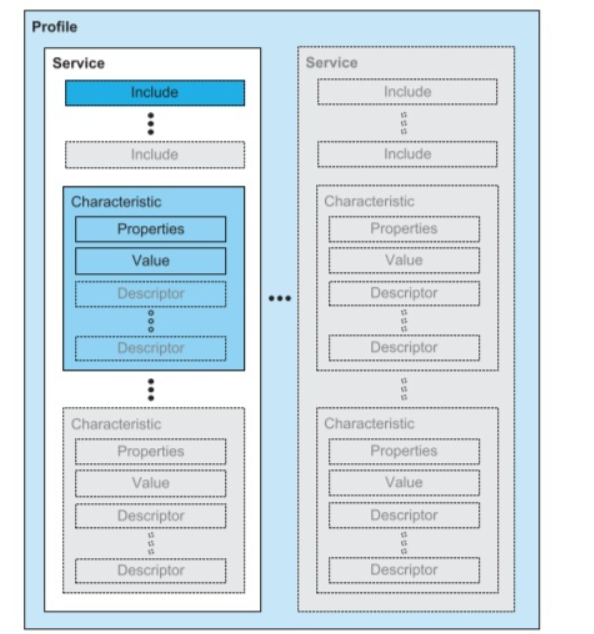
BLE蓝牙协议栈分析
BLE——协议层次结构 一、BLE Controller Controller实现射频相关的模拟和数字部分,完成最基本的数据发送和接收,Controller对外接口是天线,对内接口是主机控制器接口HCI(Hostcontroller interface); 控制…...

flutter开发实战-BackdropFilter高斯模糊子Widget控件
flutter开发实战-BackdropFilter高斯模糊子Widget。 最近开发过程中遇到需要将控件进行模糊,比如iOS的effect的模糊效果。那在flutter中就需要用到了BackdropFilter 一、BackdropFilter BackdropFilter属性定义 BackdropFilter({Key key, required ImageFilter …...
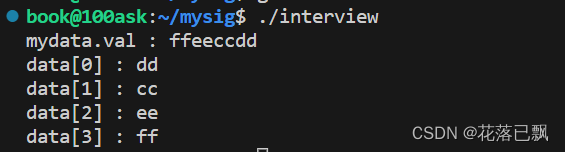
嵌入式面试刷题(day3)
文章目录 前言一、怎么判断两个float是否相同二、float数据可以移位吗三、数据接收和发送端大小端不一致怎么办四、怎么传输float类型数据1.使用联合进行传输2.使用字节流3.强制类型转换 总结 前言 本篇文章我们继续讲解嵌入式面试刷题,给大家继续分享嵌入式中的面…...

JVM源码剖析之Java命令行参数全解
最近,有一位网友询问关于Java命令行参数方面的问题,因为在Java中参数有很多种,有不少的读者一直没弄明白,所以特意写下此篇文章。 此篇文章分2大块,第一块是不同参数的解释,第2块就是JVM源码论证ÿ…...
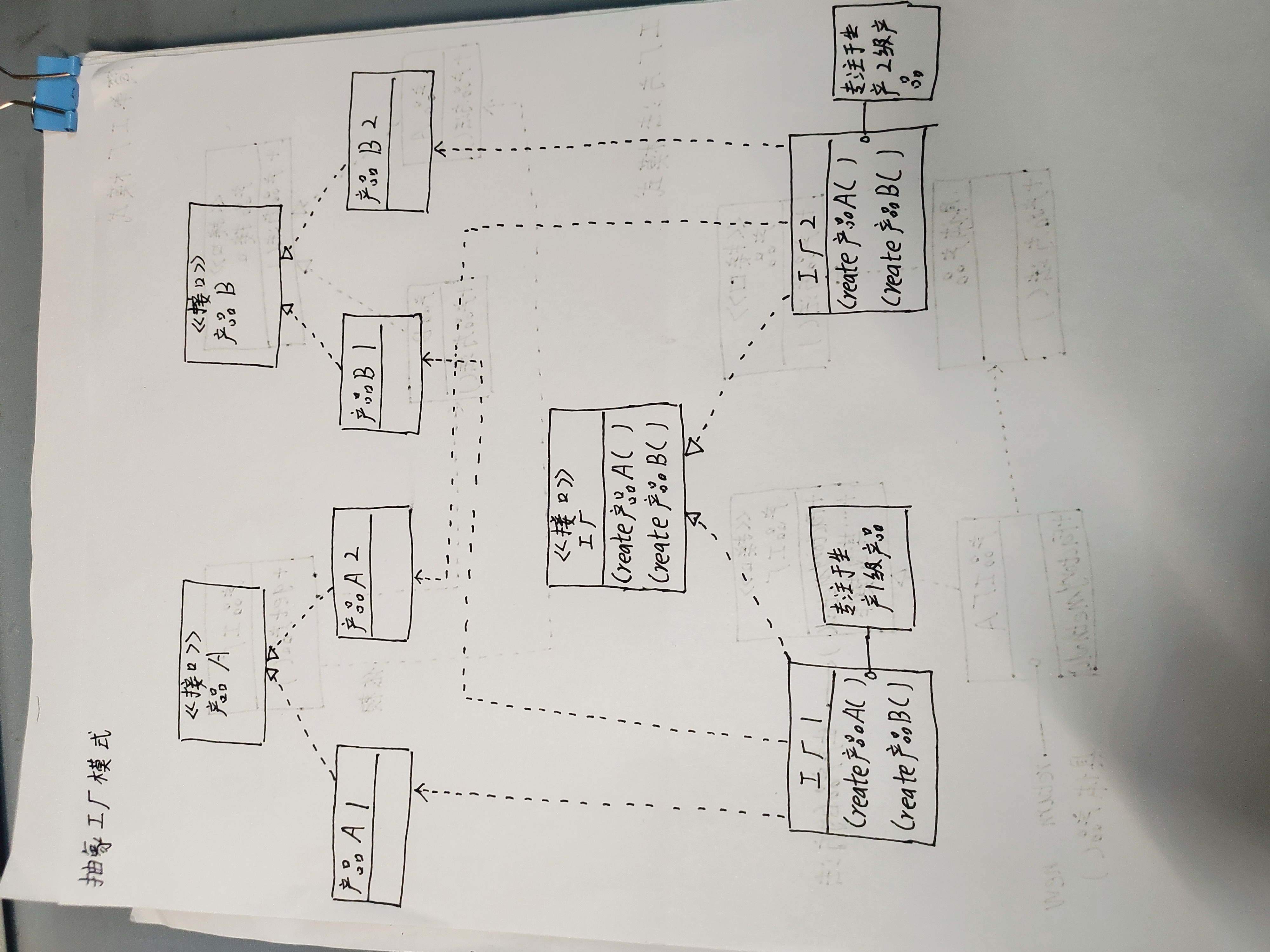
抽象工厂模式-java实现
介绍 抽象工厂模式基于工厂方法模式引入了“产品族”的概念,即我们认为具体产品是固定的,具体产品存在等级之分,比如我们常说的手机,有“青春版”,“至尊版”,“至臻版”。一个产品有多个版本族。这时候&a…...

机器学习笔记 - 基于Python发现最佳计算机视觉模型的神经架构搜索技术NAS
一、简述 近年来,随着深度学习技术的兴起,计算机视觉领域取得了巨大进步。事实证明,卷积神经网络 (CNN) 在图像识别任务中异常强大,但针对特定问题设计最佳架构仍然是一项具有挑战性的任务。这就是神经架构搜索(NAS)发挥作用的地方。NAS 是一种尖端技术,可以自动发现高性…...

机器学习---自编码器
自编码器过程 输入一个图片,经过encoder变成一个向量,再通过decoder将这个向量反向生成输入的图片。 这里我们希望输入和输出越接近越好。这个过程我们称为重建。 特点:不需要任何的标注资料。 在2006年这个思想就被提出来了: …...
vuejs 设计与实现 - 渲染器的设计
渲染器与响应式系统的结合 本节,我们暂时将渲染器限定在 DOM 平台。既然渲染器用来渲染真实 DOM 元素,那么严格来说,下面的函数就是一个合格的渲染器: // 渲染器: function renderer(domString, container) {container.innerHTM…...

openCV 图像对象的创建和赋值
文章目录 一、赋值二、克隆三、拷贝四、初始化 一、赋值 赋值操作是将一个cv::Mat对象的数据复制到另一个对象中。赋值操作使用的是浅拷贝(shallow copy),即两个对象共享相同的数据内存。这意味着对一个对象的修改会影响到另一个对象 cv::M…...
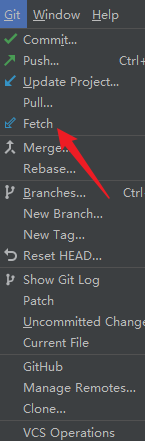
idea - 刷新 Git 分支数据 / 命令刷新 Git 分支数据
一、idea - 刷新 Git 分支数据 idea 找到 fetch 选项,重新获取分支数据 二、命令刷新 Git 分支数据 git fetch参考链接 1. 远程Gitlab新建的分支在IDEA里不显示...
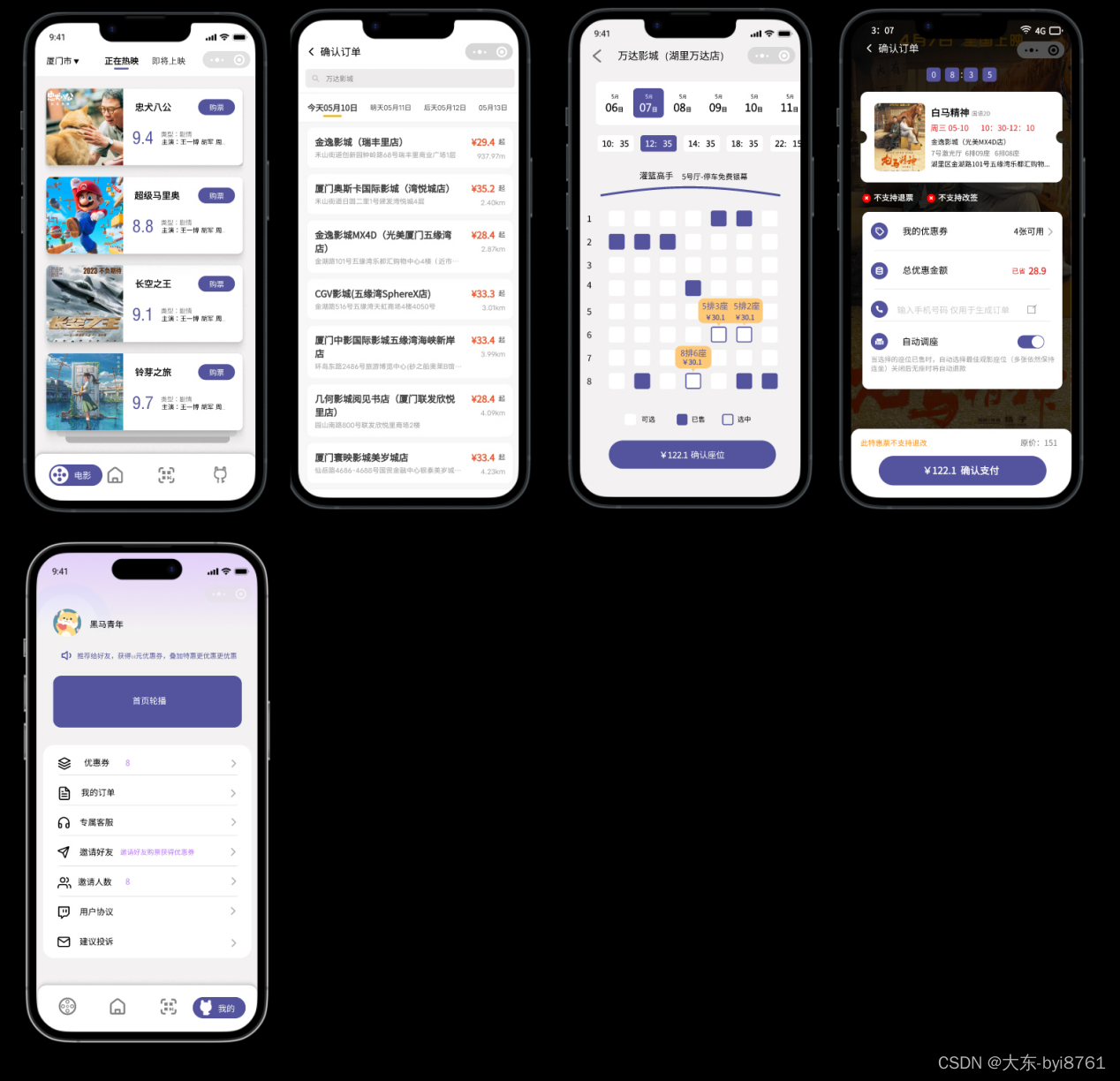
线上电影购票选座H5小程序源码开发
搭建一个线上电影购票选座H5小程序源码需要一些基本的技术和步骤。以下是一个大致的搭建过程,可以参考: 1. 确定需求和功能:首先要明确你想要的电影购票选座H5小程序的需求和功能,例如用户登录注册、电影列表展示、选座购票、订单…...

QT正则校验
文章目录 前言一、Qt正则校验1.对输入框进行校验,不允许输入其他字符2.直接校验字符串 二、常用正则校验表达式 前言 项目中会经常遇到需要对字符串进行校验的情况,需要用到正则表达式(Regular Expression,通常简写为RegExp、RE等…...

ChatGPT“侵入”校园,教学评价体制受冲击,需作出调整
北密歇根大学的教授奥曼在学生作业中发现了一篇关于世界宗教的“完美论文”。“这篇文章写得比大多数学生都要好......好到不符合我对学生的预期!”他去问ChatGPT:“这是你写的吗?”ChatGPT回答:“99.9%的概率是的。” ChatGPT“侵…...
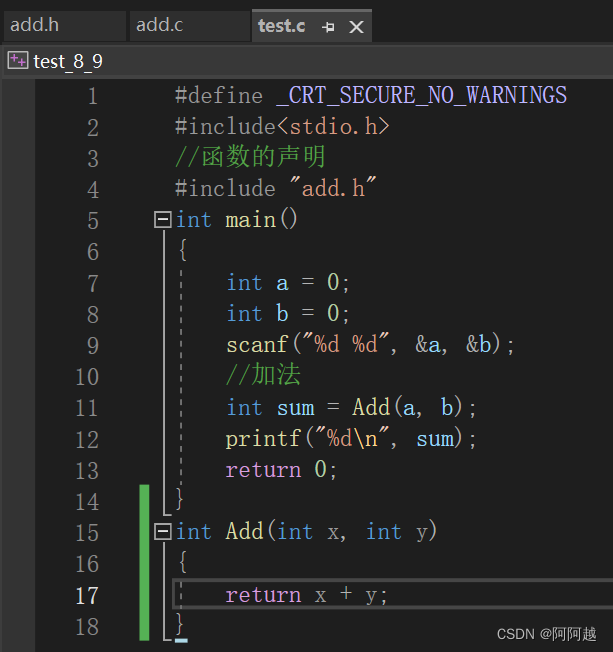
函数的声明和定义
1、函数声明 //告诉编译器有一个函数叫什么,参数是什么,返回类型是什么。但是具体是不是存在,函数声明决定不了。 //函数的声明一般出现在函数的使用之前。要满足先声明后使用。 //函数的声明一般要放在头文件中的。 2、函数的定义 //函数…...
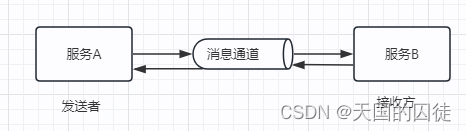
06微服务间的通信方式
一句话导读 微服务设计的一个挑战就是服务间的通信问题,服务间通信理论上可以归结为进程间通信,进程可以是同一个机器上的,也可以是不同机器的。服务可以使用同步请求响应机制通信,也可以使用异步的基于消息中间件间的通信机制。同…...

研发工程师玩转Kubernetes——local型PV和PVC绑定过程中的状态变化
PV全称是PersistentVolume,即持久卷,是由管理员事先准备好的资源。它可以是本地磁盘,也可以是网络磁盘。 PVC全称是PersistentVolumeClaim,即持久卷申领。它表示卷的使用者,对PV的申请。即我们可以认为,PV是…...
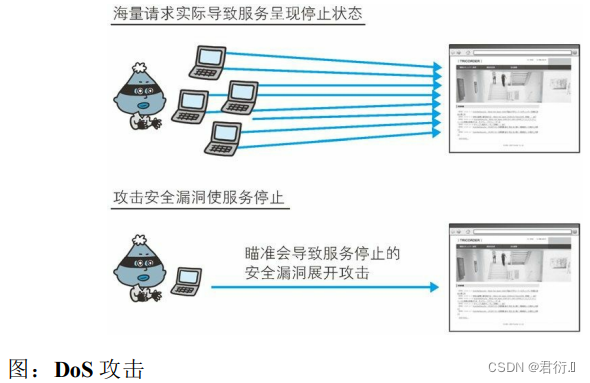
HTTP——十一、Web的攻击技术
HTTP 一、针对Web的攻击技术1、HTTP 不具备必要的安全功能2、在客户端即可篡改请求3、针对Web应用的攻击模式 二、因输出值转义不完全引发的安全漏洞1、跨站脚本攻击2、SQL 注入攻击3、OS命令注入攻击4、HTTP首部注入攻击5、邮件首部注入攻击6、目录遍历攻击7、远程文件包含漏洞…...

Python-OpenCV中的图像处理-图像金字塔
Python-OpenCV中的图像处理-图像金字塔 图像金字塔高斯金字塔拉普拉斯金字塔 金字塔图像融合 图像金字塔 同一图像的不同分辨率的子图集合,如果把最大的图像放在底部,最小的放在顶部,看起来像一座金字塔,故而得名图像金字塔。cv2…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
