DAY19
题目一

空间尝试模型 一个样本做行一个样本做列
范围尝试模型 以....做分隔
dp[i][j] 为以i为左界限 以j为右界限 求这个范围内的计算值(不对 是方法数)
这& | ^ 都是双目运算符 观察一下规律 整体字符数量一定为奇数(包括运算符和数字) 对应到数组中 数组的位一定是偶数 所以每个奇数行奇数列都不要 L不能超过R 下半区也不要(经典空间尝试模型)
那条件转移是什么呢 假设左界限 有界限 中间值为 x 那么i....x-1 x+1.....j 注意审题 是可以加括号也就是说可以决定运算顺序 也就是说 一个字符串的结果 不是固定的
条件转移是什么呢 假设左界限 有界限 中间有个位置为 x 那么i....x-1 x+1.....j
这个x位置肯定是个符号 自己举个例子就知道喵
当这个符号为&的时候 那简单 左边和右边都为1 结果才为1 左边右边有一个是0 都是0 总之就是左右相乘
但是|就比较麻烦 左1右0 为1 左0右1 为1 左1右1 为1 左0右0 为0
^呢 异或是 左1右1 为0 左0右1 左1右0 为1 左0右0 为0.
然后在这个基础呢 假如说 拿& 我左侧有3种方法为1 右侧有三种方法为1 那么我总的true的方法为 3*3对吧 记住这个dp[i][j]是方法数
所以要有两个dp数组 tdp 和 fdp 分别表示L到R范围内的(true/false)的方法数
basecase 是L==R的时候 如果是1 的话 那就是 tdp 当前位置有一种方法 0就是fdp位置有一种方法
否则为0
public static int ExpressionNumber0(String express, boolean desired){char [] chars = express.toCharArray();int N = chars.length;int [][] tdp = new int [N][N];int [][] fdp = new int [N][N];for(int i = 0;i<N;i+=2) {tdp[i][i] = chars[i] == '1'?1:0;//不用单引号就是ASCII码了fdp[i][i] = chars[i] == '0'?1:0;}for (int row = N - 3; row >= 0; row -= 2) {for (int col = row + 2; col < N; col += 2) {//行等于列的已经填完了 这次往上移动一下 就是两个格子 //col<的是N哦 所以是一行之内 先填前面 再填后面 所以可以依赖左方和下方for (int i = row + 1; i < col; i += 2) {//用这个i枚举每一个分界点 顺便说下既然依赖于左下的格子switch (chars[i]) {//注意这里行+1 是符号的位置 我得用它来确定转移方程 +1-1是格子的位置 格子的位置不能是符号位case ('&')://记住是+= 这是累加的tdp[row][col] += tdp[row][i-1]*tdp[i+1][col];fdp[row][col] += fdp[row][i-1]*fdp[i+1][col]+fdp[row][i-1]*tdp[i+1][col]+tdp[row][i-1]*fdp[i+1][col];break;case('|'):tdp[row][col] += tdp[row][i-1]*fdp[i+1][col] + fdp[row][i-1]*tdp[i+1][col]+tdp[row][i-1]*tdp[i+1][col];fdp[row][col] += fdp[row][i-1]*fdp[i+1][col];break;case('^'):tdp[row][col] += tdp[row][i - 1] * fdp[i + 1][col]+fdp[row][i - 1] * tdp[i + 1][col];fdp[row][col] += tdp[row][i - 1] * tdp[i + 1][col]+fdp[row][i - 1] * fdp[i + 1][col];break;} }}}return desired?tdp[0][N-1]:fdp[0][N-1];}题目二
给一个数组 划分多个数组 在哪一种划分下 能让异或和为0的更多
经典的从左往右尝试模型+范围尝试模型
dp[i] 表示从0...i最多有多少0
我们假设这种分法是 最多0的
(1) 当i位置(所属的块)异或和不为0的时候 dp[i] = dp[i-1]
(2) 当i位置(所属的块)异或和为0
假设答案法 假如说当前分法是最佳答案
假如其中有任意一块区域j...i那这之间肯定不存在一个k 让k...i异或和为0 因为你这相当于又切了 一块 我们开始已经假定这个是最优答案了 这就冲突了
那假设我们的最后一块区域为j....i 这个j 一定是 离i最近的 能让这块区域异或和为0的 0^0==0 所以
0....j j+1....i异或和都为0 我们找到j位置的答案 它再+1(我们现在说的这一块) 结果就是i位置的答案
public static int MostEOR(int [] arr) {if (arr == null || arr.length == 0) {return 0;}int [] dp = new int [arr.length];dp[0] = arr[0]==0?1:0; HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();int eor = 0;map.put(0, -1);map.put(arr[0],0);for(int i = 1;i<arr.length;i++) {eor^=arr[i];if(map.containsKey(eor)) {int pre = map.get(eor);dp[i] = pre == -1 ? 1 : (dp[pre] + 1);//如果等于-1 就是异或和为0 直接算一种 当然如果后面又有0出现 那就回替换掉最开始的//它只对应一种情况 从0...i累加和就是 0 且中间还没出现过其他的0 所以它只有一个0}dp[i] = Math.max(dp[i - 1], dp[i]);map.put(eor, i);}return dp[dp.length - 1];}和子序列一样 都是可能性的组织 几个可能性里面取一个most 既然要求最长/多 那就用most 是不是有点牵强了
我老觉得是 既然最后只有一种情况作为答案了 那为什么还要多个比较
答:有多种if 每种情况都可以选择 他们都是存在的 只是看我们的选择哪个作为这个位置的答案而已 所以选择多的那个
题目三
给出一组正整数arr,你从第0个数向最后一个数,
每个数的值表示你从这个位置可以向右跳跃的最大长度
计算如何以最少的跳跃次数跳到最后一个数。
首先我们要理解 不是每个点都跳到最远好 因为你可能会错过一个大长度
而且这个模型不用考虑往回跳 因为你完全可以中间停下来 为啥要往回跳
五步最远能跳多远
四步最远的地方 一定比五步最远跳的近(废话)
四步每个能到的位置 加上自身的值 其中一定有一个是五步的右边界(走到最远的地方)
第一步我可以走到 i的位置 也就是说第一步的区间是0...i 这个区间里我可以选择任何一个地方作为落脚点 走第二步 但是目前我们看不出 我们可以选择在哪落脚是迈出第二步是最优解 不过没关系 我们直接枚举每一个落脚点 看看最远能走到哪 也就是找出第三步的区间...以此类推 看看最先什么时候扩到对应区间
感觉有哪不通?我也是
对于第四步来说 假如我选了其中一个落脚点 那么我这个落脚点走不到5步的区间的最右怎么办?那就不要选啊 就选能到达最边界的步 那我到达了最边界 最边界上面的步数 是一个很小的点那下一步怎么扩充 无所谓啊 我们会枚举每一个落脚点 来扩充下一步 对于每一个区间 它的每一点都是可达的 然后用它扩充出来的区间 也一样是可达的 所以不同区间所有点都是可达的 如果这个点肯定是上一个区间的某个点跳过来的 那这个调过来的点 也是上上个区间调过来的
public static int jump(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int step = 0; // 跳了多少步int cur = 0; // step步内,右边界int next = 0;// step+1步内,右边界for (int i = 0; i < arr.length; i++) {if (cur < i) {step++;cur = next;}next = Math.max(next, i + arr[i]);}return step;}被笔记骗了 压根没有什么flag -1
相关文章:

DAY19
题目一 空间尝试模型 一个样本做行一个样本做列 范围尝试模型 以....做分隔 dp[i][j] 为以i为左界限 以j为右界限 求这个范围内的计算值(不对 是方法数) 这& | ^ 都是双目运算符 观察一下规律 整体字符数量一定为奇数(包括运算符和数字) 对应到数组中 数组的位一定是偶数…...

Data analysis|Tableau基本介绍及可实现功能
一、基础知识介绍 (一)什么是tableau tableau 成立于 2003 年,是斯坦福大学一个计算机科学项目的成果,该项目旨在改善分析流程并让人们能够通过可视化更轻松地使用数据。Tableau可以帮助用户更好地理解和发现数据中的价值&#x…...

单元测试优化:为什么要对程序进行测试?测试有什么好处?
单元测试(Unit Testing)又称为模块测试, 是针对程序模块(软件设计的最小单位)来进行正确性检验的测试工作。 程序单元是应用的最小可测试部件。简单来说,就是测试数据的稳定性是否达到程序的预期。 我们日常开发时可能…...
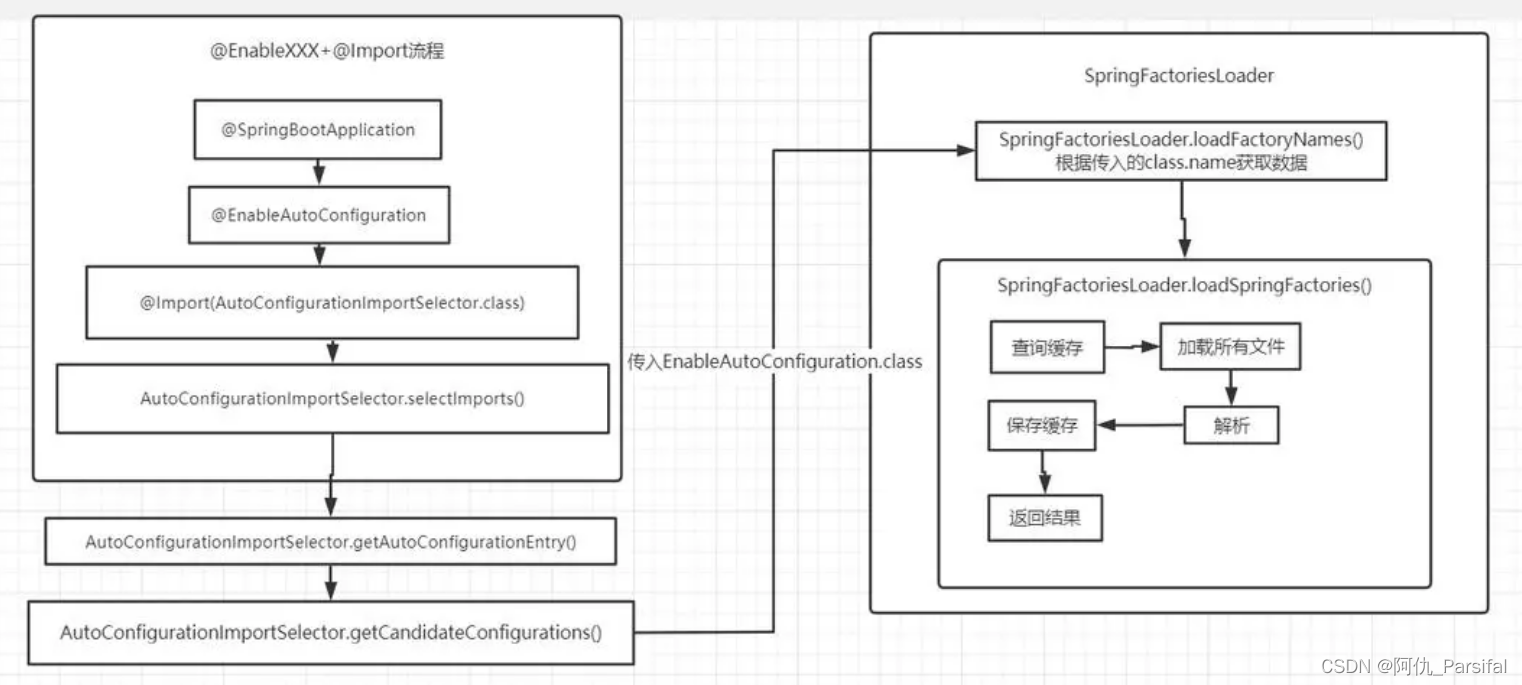
自动装配在Spring Boot中的重要性及实现方式
这里写目录标题 自动装配在Spring Boot中的重要性及实现方式什么是自动装配?如何实现自动装配?如何使用自动装配自动装配的优势总结 手写自动装配的Java代码示例原理 自动装配在Spring Boot中的重要性及实现方式 Spring Boot是基于Spring框架的开源框架…...

校对软件在司法系统中的应用:加强刑事文书审查
校对软件在司法系统中的应用可以加强刑事文书审查,提高文书的准确性和可靠性。 以下是校对软件在刑事文书审查方面的应用: 1.语法和拼写检查:校对软件可以自动检查刑事文书中的语法错误和拼写错误。这包括句子结构、主谓一致、动词形式等方面…...
微信小程序上传图片和文件
1.从微信里选择图片或文件上传 使用的vant的上传组件 原生用 wx.chooseMessageFile() html <!-- 从微信上面选择文件 --><van-uploader file-list"{{ file }}" bind:after-read"afterRead" max-count"{{3}}" deletable"{{ true…...
拥抱AIGC浪潮,亚信科技将如何把握时代新增量?
去年底,由ChatGPT带起的AIGC浪潮以迅雷不及掩耳之势席卷全球。 当互联网技术的人口红利逐渐消退之际,AIGC就像打开通用人工智能大门的那把秘钥,加速开启数智化时代的到来。正如OpenAI CEO Sam Altman所言:一个全新的摩尔定律可能…...

【opencv】指定宽或高按比例缩放图片 拼接图片
指定宽或高按比例缩放图片 import cv2def resize_by_ratio(image, widthNone, heightNone, intercv2.INTER_AREA):img_new_size None(h, w) image.shape[:2] # 获得高度和宽度if width is None and height is None: # 如果输入的宽度和高度都为空return image # 直接返回原图…...
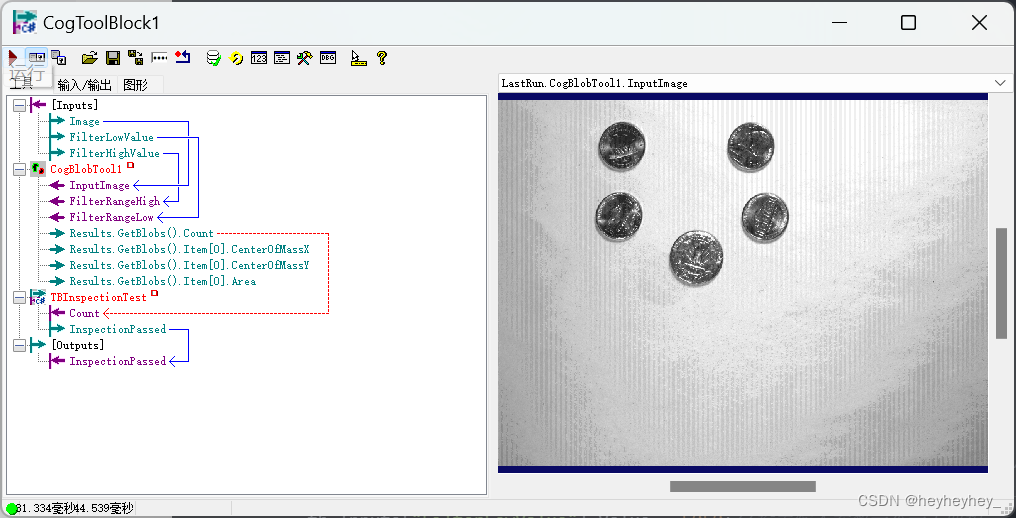
使用C#加载TOOLBLOCK
前言 因为Vpp文件类型包含了以下三种 QuickBuidJobToolBlock 不同类型的打开方式不同,需要提前知道vpp是什么类型 例如 这个TB.vpp文件是TOOLBLOCK,就不能直接在visionpro中打开(直接打开需要QuickBuid文件), 可以…...
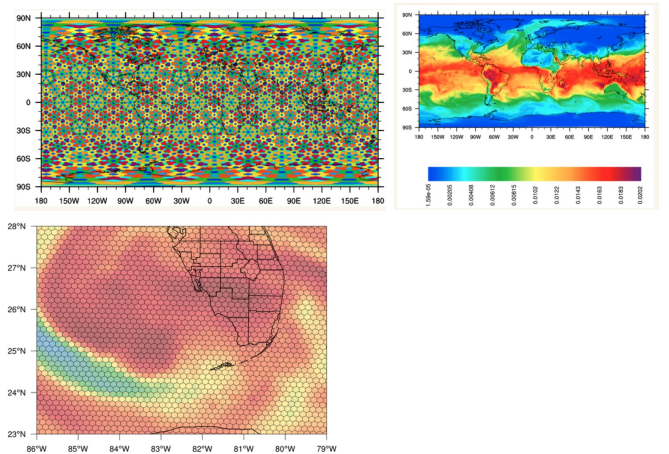
MPAS-A原理及陆面模式的基本概念
跨尺度预测模式(The Model for Prediction Across Scales - MPAS)是由洛斯阿拉莫斯实验室和美国国家大气研究中心(NCAR)共同开发,其由3个部分组成,分别称为 MPAS-A(大气模型)、MPAS-O(海洋模型&…...

前端技术Html,Css,JavaScript,Vue3
Html 1.基本标签 <h1>最大的标题</h1> <h2> . . . </h2> <h3> . . . </h3> <h4> . . . </h4> <h5> . . . </h5> <h6>最小的标题</h6><p>这是一个段落。</p> <br> (换…...

实战项目——多功能电子时钟
一,项目要求 二,理论原理 通过按键来控制状态机的状态,在将状态值传送到各个模块进行驱动,在空闲状态下,数码管显示基础时钟,基础时钟是由7个计数器组合而成,当在ADJUST状态下可以调整时间&…...

【es6】对象解构赋值
es6中对象解构赋值: 代码 let { foo: baz } { foo: rose, bar: jeck }; baz // "rose"let obj { first: tom, last: rose }; let { first: f, last: l } obj; f // tom l // roselet { foo: baz } { foo: rose, bar: jeck }中的foo:baz部分ÿ…...

腾讯云服务器CVM标准型S6详细介绍_性能测评
腾讯云服务器CVM标准型S6实例是最新一代的标准型实例,CPU采用Intel Xeon Ice Lake处理器,主频2.7GHz,睿频3.3GHz,内存采用最新 DDR4,默认网络优化,最高内网收发能力达1900万pps,最高内网带宽可支…...
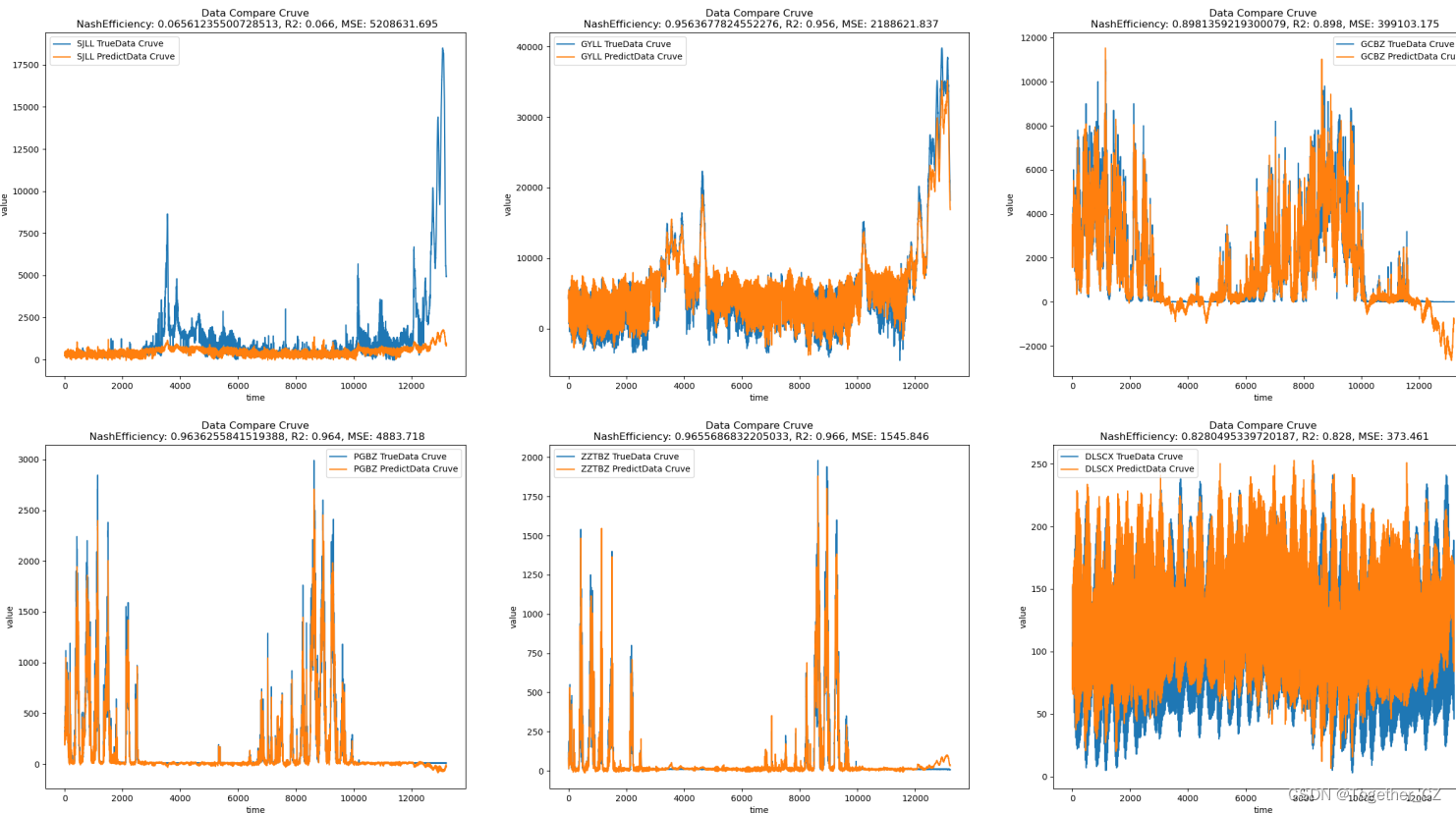
时间序列预测任务下探索深度学习参数对模型预测性能的影响
时间序列相关的项目在我之前的很多博文中都有涉及,覆盖的数据领域也是比较广泛的,很多任务或者是项目中往往是搭建出来指定的模型之后就基本完成任务了,比较少去通过实验的维度去探索分析不同参数对模型性能的影响,这两天正好有时…...
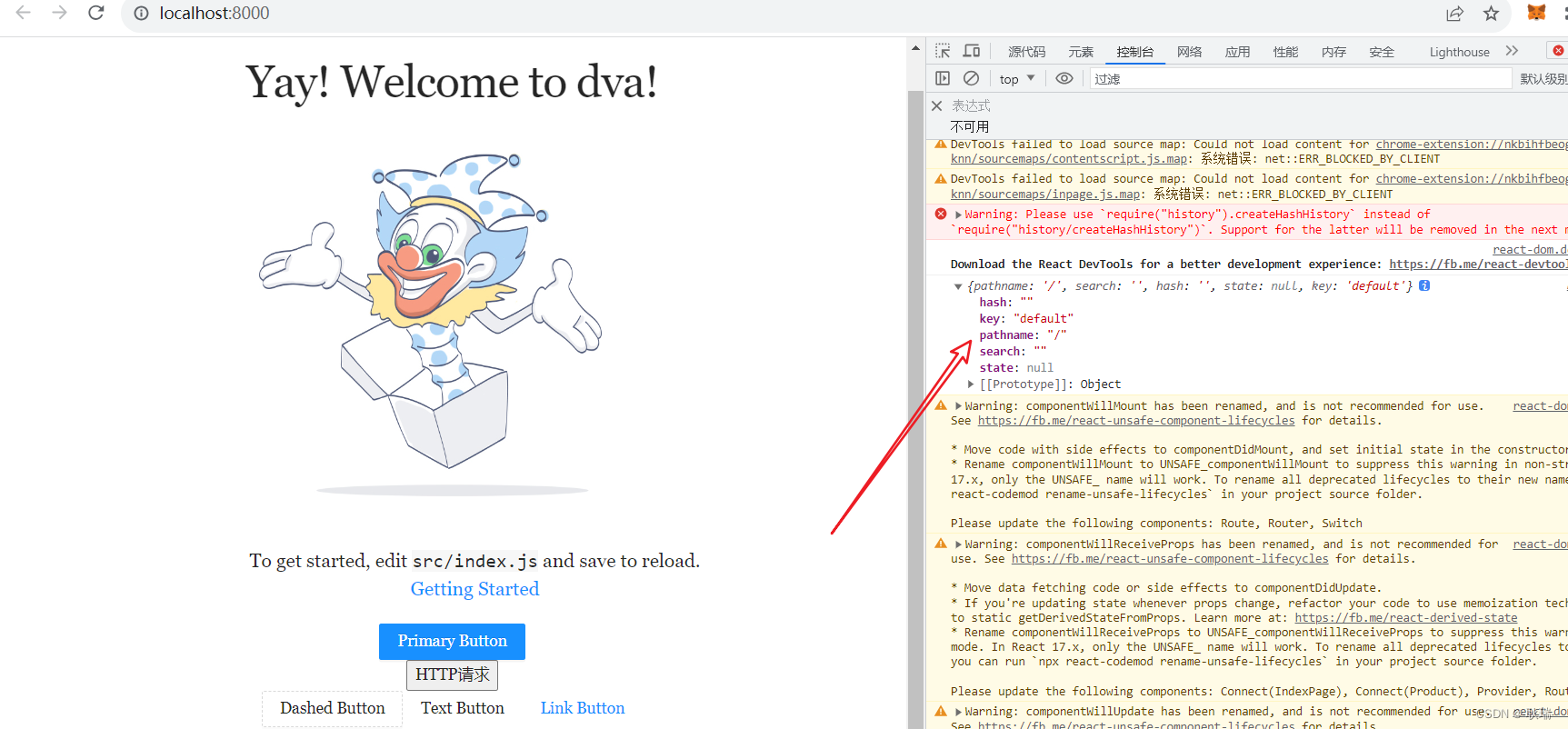
React Dva项目 简单引入models中的所有JS文件
我们前面接触的 Dva项目 models目录下的文件还要一个一个引入 其实体验并不是很好 而且如果项目很大那就比较麻烦了 我们可以在 models 下创建一个 index.js 文件 编写代码如下 const context require.context("./", false, /\.js$/); export default context.key…...
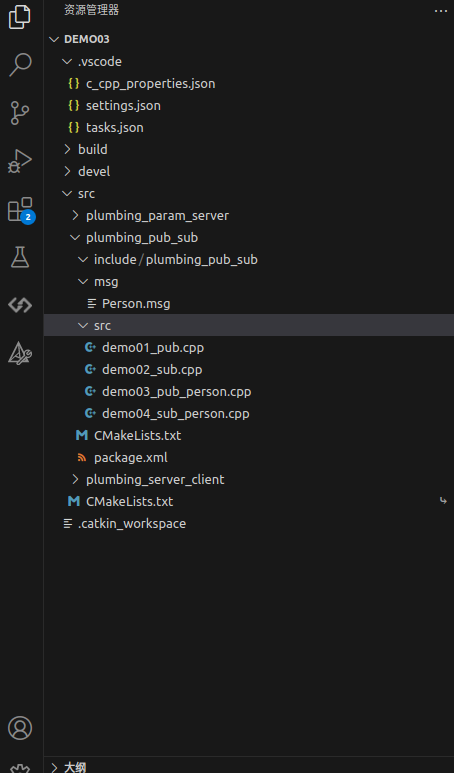
ROS入门-第 1 章 ROS概述与环境搭建
目录 第 1 章 ROS概述与环境搭建 1.1 ROS简介 1.1.1 ROS概念 1.1.2 ROS设计目标 1.1.3 ROS发展历程 1.3 ROS快速体验 1.3.1 HelloWorld实现简介 1.3.2 HelloWorld(C版) 步骤 1:创建工作空间 步骤 2:创建发布者节点 步骤…...
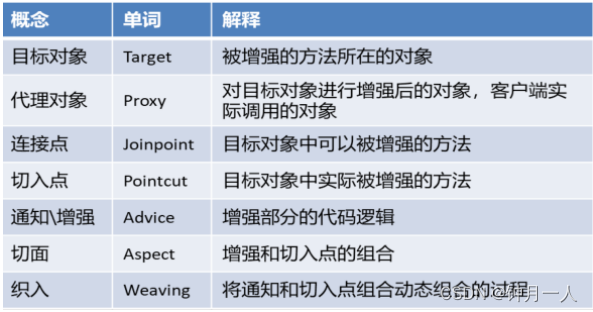
spring之AOP简单介绍
1.AOP的概念 AOP,Aspect Oriented Programming,面向切面编程,是对面向对象编程OOP的升华。OOP是纵向对一个 事物的抽象,一个对象包括静态的属性信息,包括动态的方法信息等。而AOP是横向的对不同事物的抽象,…...

使用Spark ALS模型 + Faiss向量检索实现用户扩量实例
1、通过ALS模型实现用户/商品Embedding的效果,获得其向量表示 准备训练数据, M (U , I, R) 即 用户集U、商品集I、及评分数据R。 (1)商品集I的选择:可以根据业务目标确定商品候选集,比如TopK热度召回、或…...

Jmeter入门之digest函数 jmeter字符串连接与登录串加密应用
登录请求中加密串是由多个子串连接,再加密之后传输。 参数连接:${var1}${var2}${var3} 加密函数:__digest (函数助手里如果没有该函数,请下载最新版本的jmeter5.0) 函数助手:Options > …...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
