【C++】红黑树模拟实现插入功能(包含旋转和变色)
红黑树模拟实现并封装为map和set
- 前言
- 正式开始
- 红黑树概念
- 红黑树基本要求
- 大致框架
- 树节点
- 树
- 调整红黑树使其平衡
- 第一种:cur红,p红,g黑,u存在且为红
- 第二种:cur红,p红,g黑,u不存在或为黑
- 左左,右右:单旋 + 变色
- 左右,右左:双旋 + 变色
前言
本篇主要讲解红黑树的模拟实现,实现之后再封装成map和set。
红黑树中所用到的旋转功能均源自我的上一篇博客,本篇中不会再详谈旋转,若对于旋转不了解的同学可以先看看上一篇博客:【C++】AVL树模拟实现插入功能
正式开始
前一篇的AVL树,是严格平衡的一棵二叉搜索树,也就是每个节点的做右子树高度差不超过1。
红黑树,在二叉搜索树的基础上,多了一个条件:最长路径不超过最短路径的2倍。没有AVL树那么严格,但是也是近似平衡的。
同AVL树相比,插入同样的数据,AVL树旋转更多,红黑树旋转更少,红黑树的优势就在于此,这一点比AVL树优很多,毕竟每次旋转的时候还是要动不少指针的。
但同时红黑树也有一丁点的劣势,查找效率比AVL树低一丢丢,因为极端情况下,也就是最长路径就是最短路径的2倍时,当我们正好要查找最长路径的叶子节点时,速度比AVL树慢了一半。但是虽说是一半,那也只是 l o g 2 N log_2N log2N的一半,如果存储10亿个数,查找最边上的节点,也就查找30次就能找到,因为对于AVL树来说几乎是完全二分的,那么红黑树的最坏情况就是60次喽,但是这样二者相差可以说是忽略不计的。
所以考虑整体情况的话,还是红黑树更胜一筹。不然STL中的map和set底层用的就不是红黑树了。
红黑树概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
先来一棵树看看:
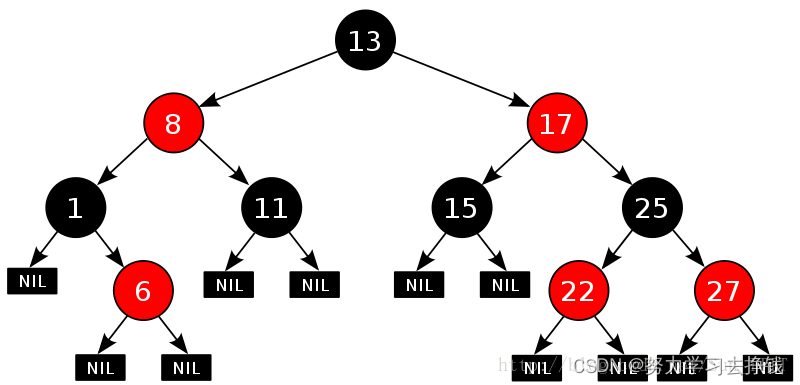
看起来花里胡哨的,不要怕,纸老虎。
红黑树基本要求
红黑树实现的时候不是按照AVL树那样依靠平衡因子来实现的。而是通过控制节点是红色还是黑色来实现的,不然也就不叫红黑树了。
但是对于节点是红色还是黑色是有要求的:
- 每个节点非黑即红
- 根节点是黑色的
- 红色节点的两个子节点为黑色的,即树中没有连续的红色结点
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。即每条路径上黑色结点数相等。
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)。
第五点其实没什么用,是指空节点是黑色节点,当树是空树的时候正好可以和第二条对应。树是空树,根节点就是空的,空节点是黑色节点,那么根节点也就是黑色结点了。
我再把上面那张图拿出来,各位对着前四点看看:
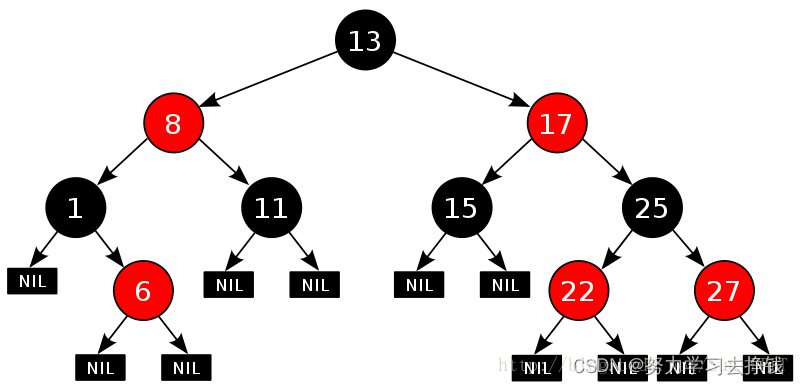
每个结点满足上述条件后就能够保证最长路径不超过最短路径的二倍了。各位想想为什么。
上述条件中可没有说不能有连续的黑色节点,所以最短路径就可以是连续黑色结点所组成的路径,最长路径就是一黑一红一黑一红…组成的路径。那么当到达极限时,最长路径就正好是最短路径的二倍。
再问个问题:
上图中,一共有几条路径?
答案是:11条。
有的同学可能懵了,不要懵。
上面数路径是要数到空节点的,上面一共有11个空节点,所以也就是11条路径。
这里也是第五点的一个好处,方便我们数路径,可以看到图中空节点写的是NIL,红黑树这里把空节点叫做NIL节点。
废话不多说了,我们先把树大致框架搞出来。
大致框架
树节点
红黑树树节点中包含的东西如下:

构造函数为:

颜色暂时不给,等会插入的时候会再说。
树
再来写树。
初始就一根:

然后把二叉搜索树的基本的插入功能写出来:

上面我把调整树结构的留下,这里细讲。
调整红黑树使其平衡
若插入新节点后的树结构不符合了前面说的那四条规则,此时就要调整。
但是插入节点要确定一下其颜色,如何确定呢?
看第三条和第四条规定。不能有连续的红色节点,所有路径黑色节点数量相同。
所以如果我们插入红色节点,影响的就只是当前插入节点所处的路径,因为红色节点不相连即可。如果我们插入黑色结点,影响的就是整棵树了,因为当前路径加一个黑的,其他路径就都要加一个黑的。显然,我们要选就选红色的插入,千万不敢选黑色的插,一选黑色就要调整棵树,选了红色只调当前路径就够了。
那么调整之前,我得先声明几个节点的名字
- cur节点,就是新插入的节点,等会在调整的过程中我以cur表示。
- . 父(father)节点 / 双亲(parent)节点, 等会在调整的过程中我以字母p表示。
- 叔叔(uncle)节点,就是父节点的兄弟,等会在调整的过程中我以字母u表示。
- 爷爷(grandfather)节点,就是父节点的父节点,等会在调整的过程中我以字母g表示。
先来个图看看:
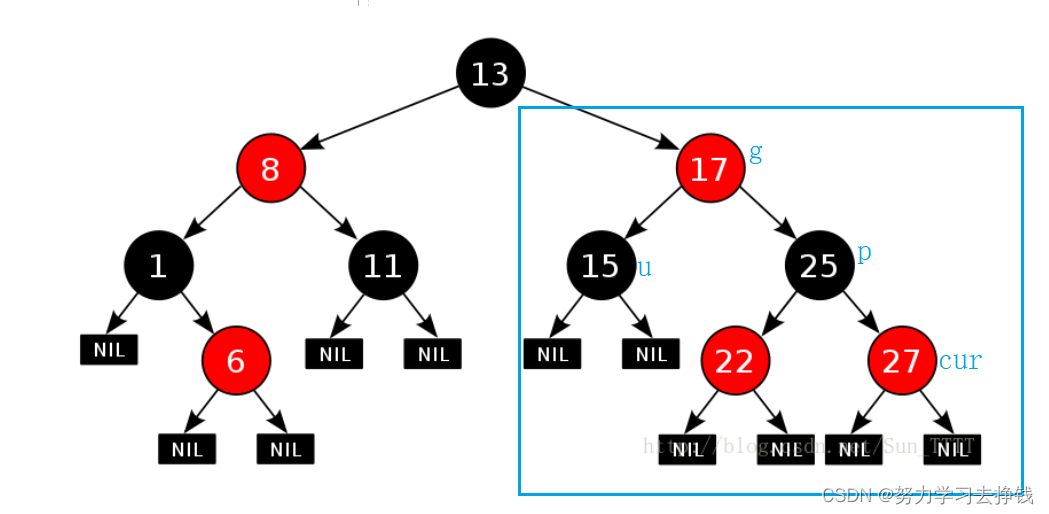
那么调整可分为两大种情况。
第一种:cur红,p红,g黑,u存在且为红
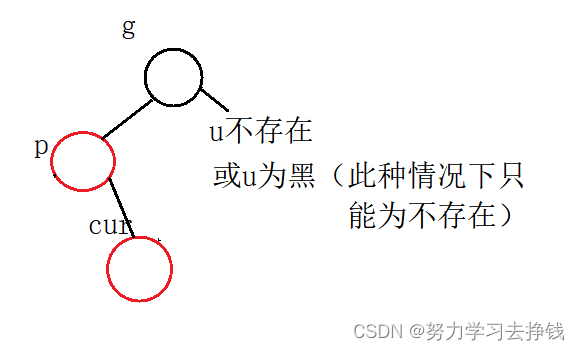
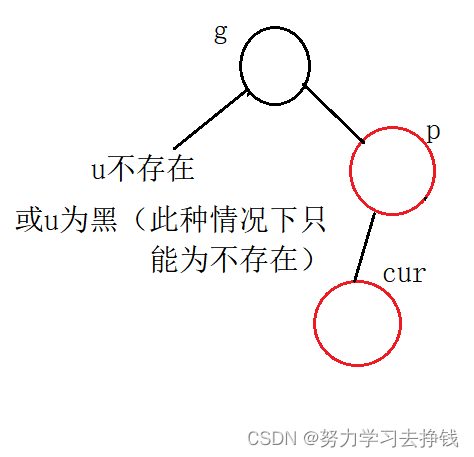
第二种:cur红,p红,g黑,u不存在或为黑
说一下为啥是上面两种。
首先我们插入的一定是红色节点。
- 树为空的时候,不需要调整,直接让根搞成黑色节点。
- 插入节点为红色,p为黑色,此时不需要调整,直接插入即可。因为前面也说了,极限长度是黑红黑红这样规律走下去的,当插入的是红色的时候,不会出现到达最长路径的情况。所以不需要调整。
- 插入节点为红色,p为红色,违反第三条规定,此时就需要调整。而且当p为红色的时候,g一定为黑色,因为原树要保证是红黑树,所以当p是红色的时候,不能有连续的红色节点,所以g就一定是黑色的。
然后将第三点的调整分为两大种,至于为什么,等会将调整的时候就知道了,这是前人总结出来的规律。
那么就开始将调整。
如果你对于AVL树插入时的旋转非常熟悉了,那么这里红黑树插入的调整自然也不在话下。
正式开始调整:
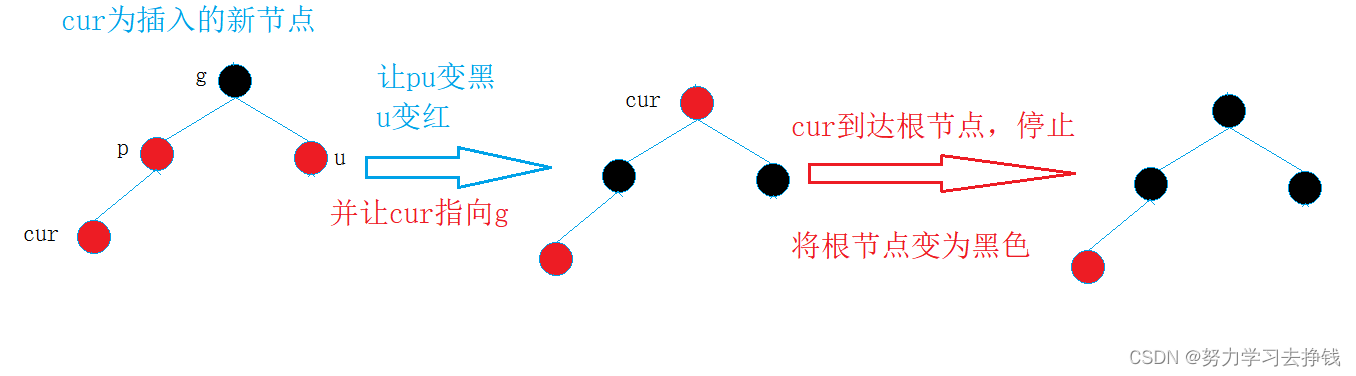
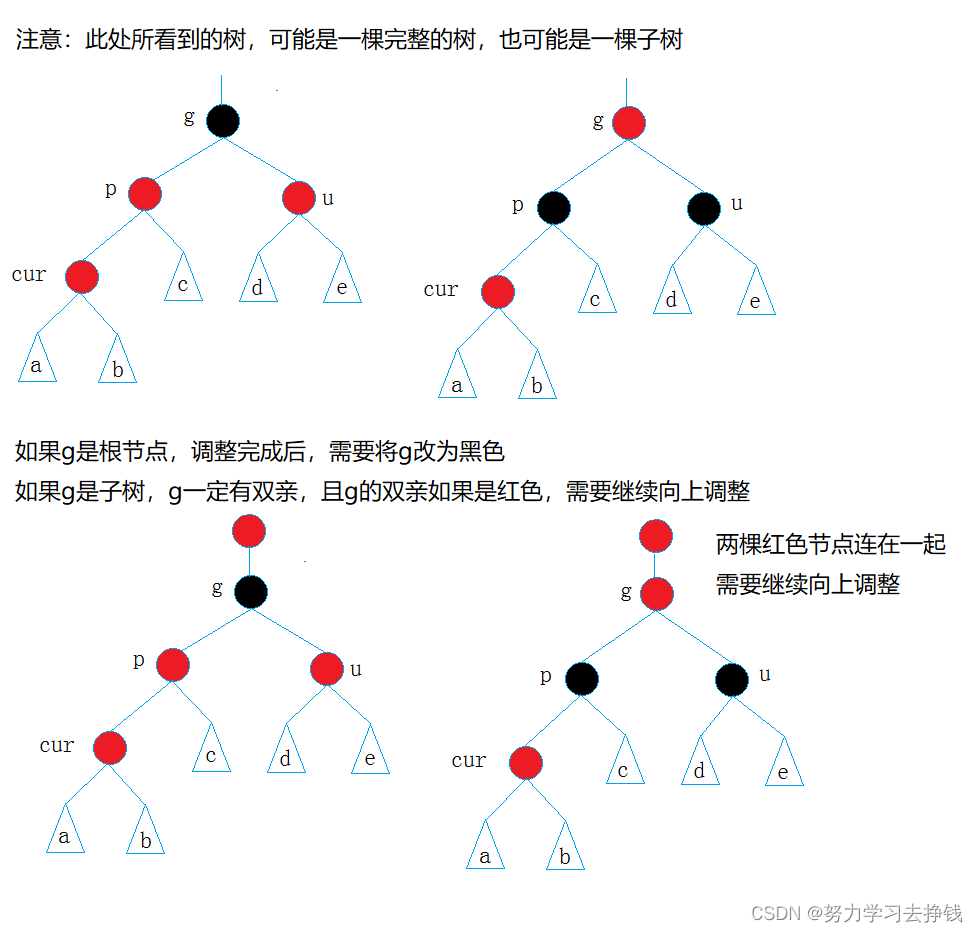
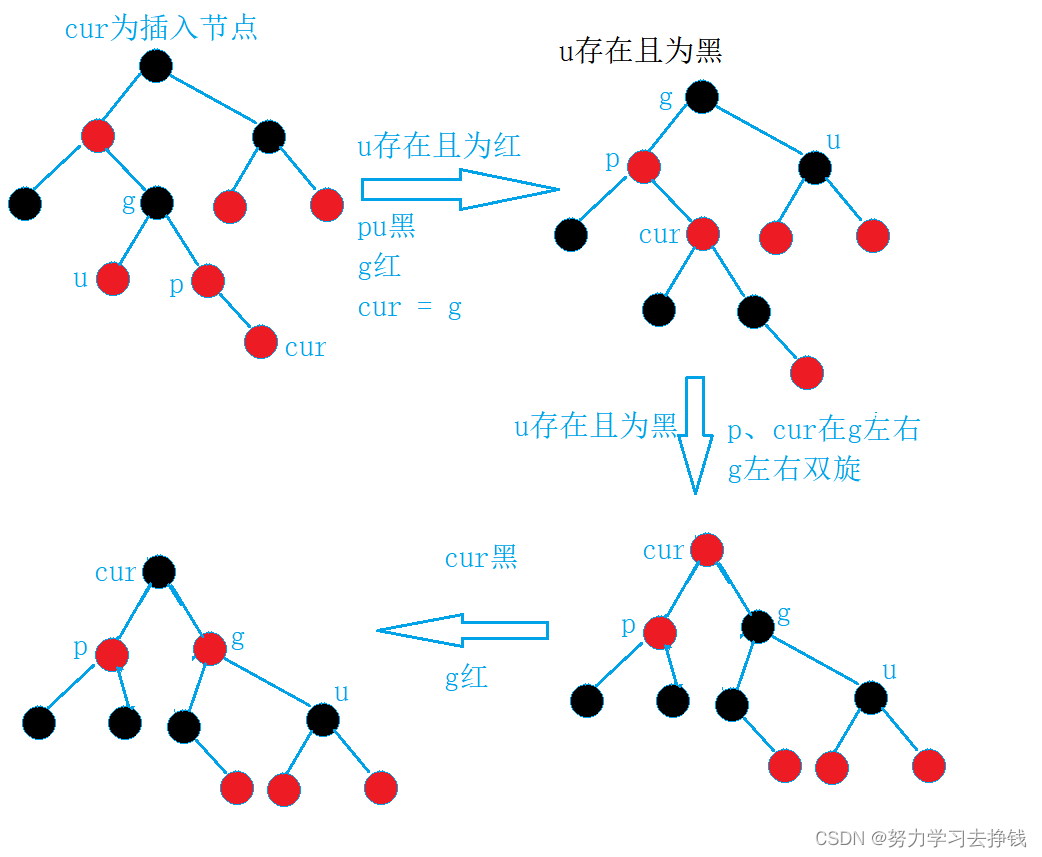
第一种:cur红,p红,g黑,u存在且为红
调整方式为:pu变黑g变红,cur指向g继续向上调整,遇到树根为止,将树根改为黑。
即只有变色。
先来两个例子:
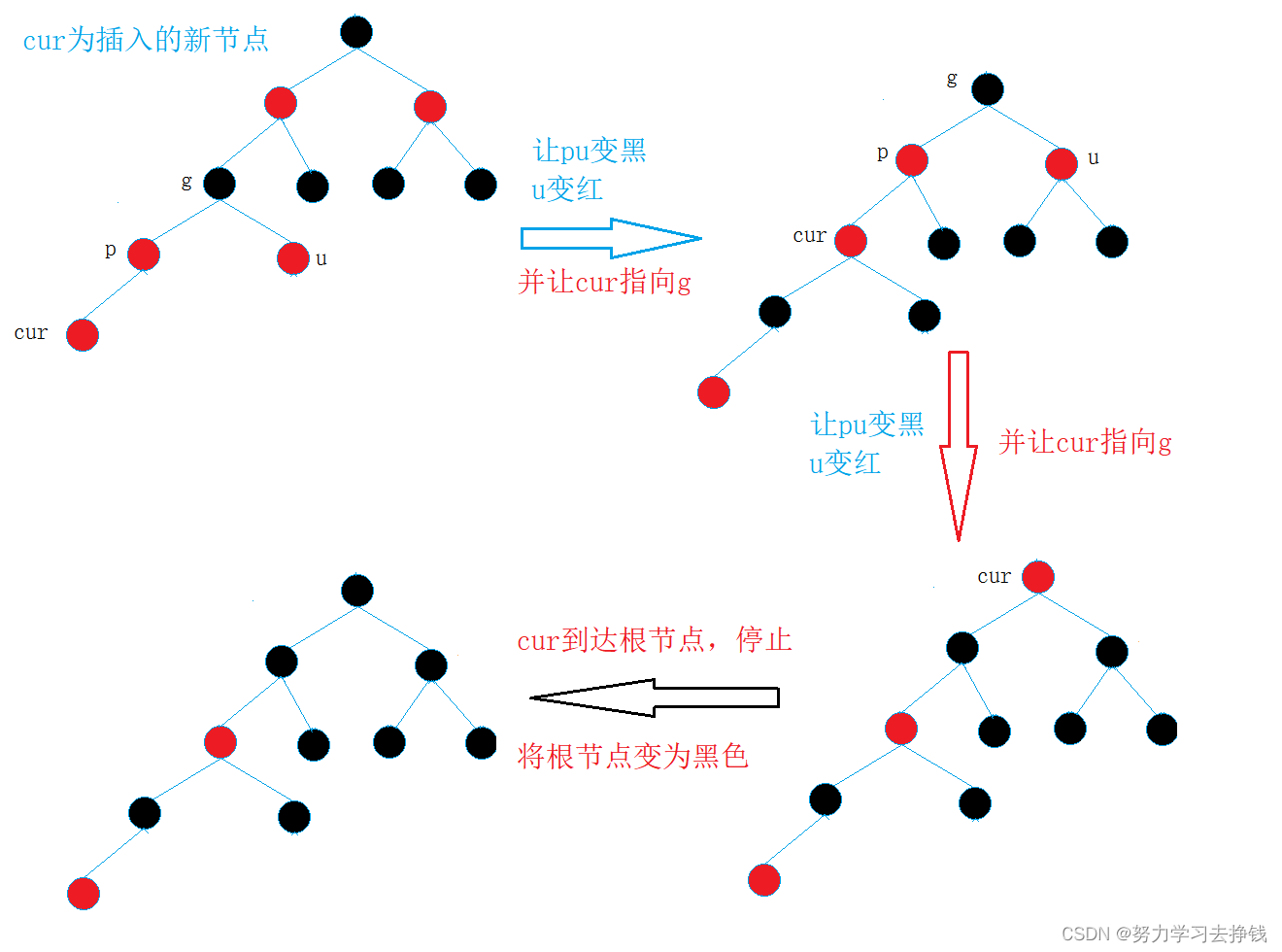
调整一次:
调整两次:
不用往下画了,再往下就是调整三、四、五……等等次数了。是有规律的,上面两个都是具象图,下来我把抽象图给大家,各位参考参考:
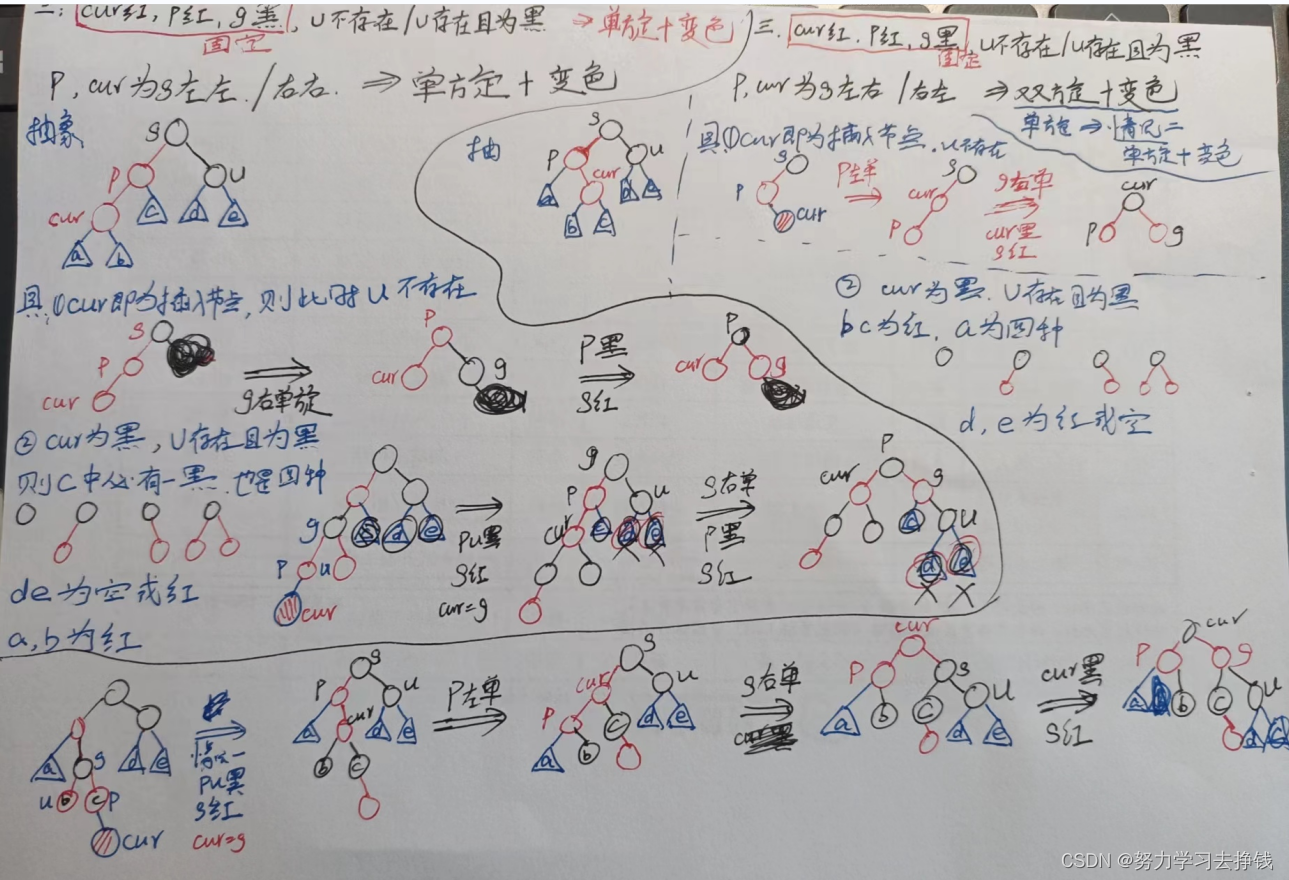
附上我手画的图:
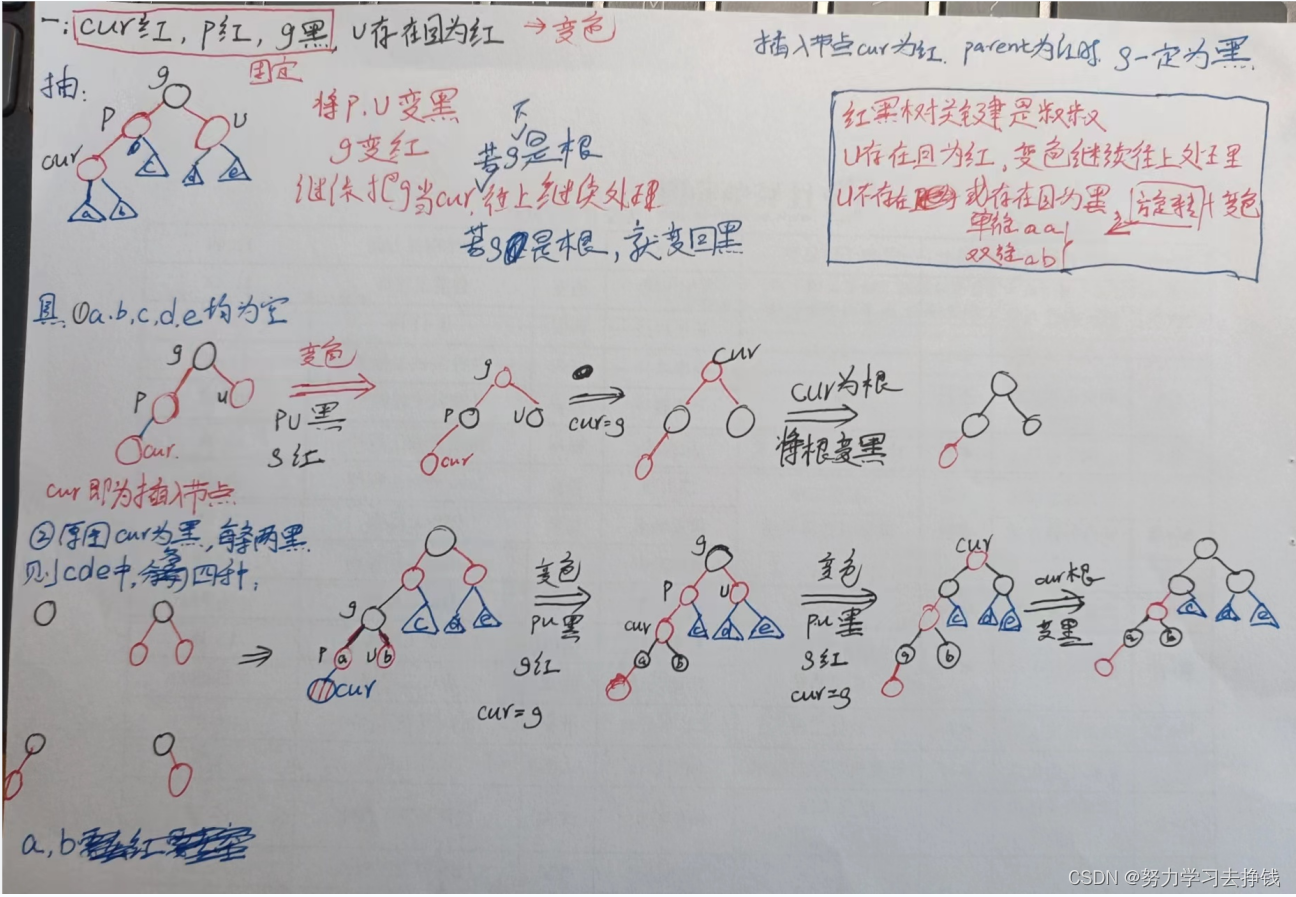
比较潦草,主要是方便我看一下。
这里不管cur在p左边还是右边,调整方式都是一样的,记住最开始写的调整方式就行:
调整方式为:pu变黑g变红,cur指向g继续向上调整,遇到树根为止,将树根改为黑。
即只有变色。
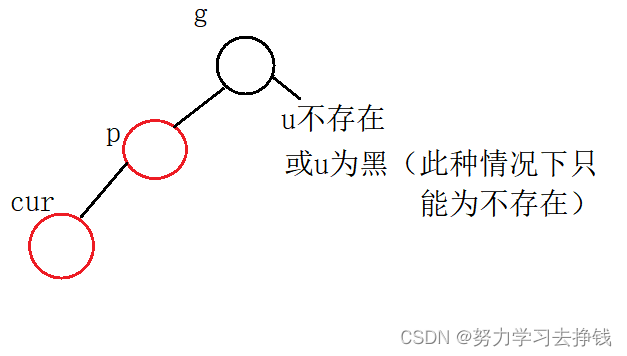
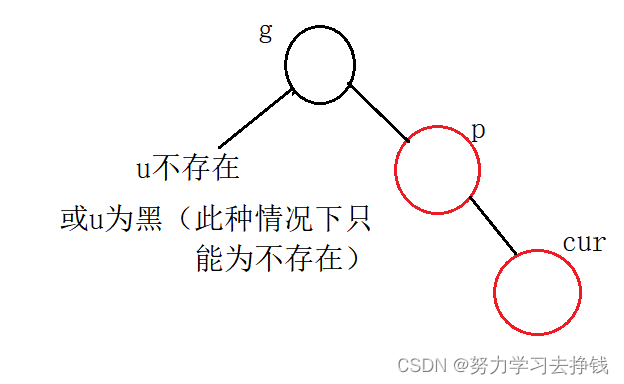
第二种:cur红,p红,g黑,u不存在或为黑
第二大种就要用到旋转了,但还要再分为两小种。
第一小种:p在g左且cur在p左,或者p在g右且cur在p右。此种情况下为单旋。
对应的图为:
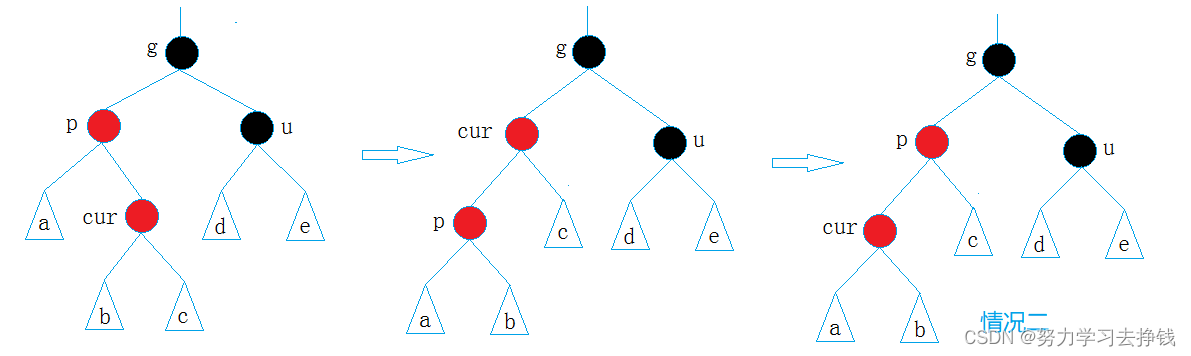
第二小种:p在g左且cur在p右,或者p在g右且cur在p左。此种情况下为双旋。
对应图为:
然后再细谈:
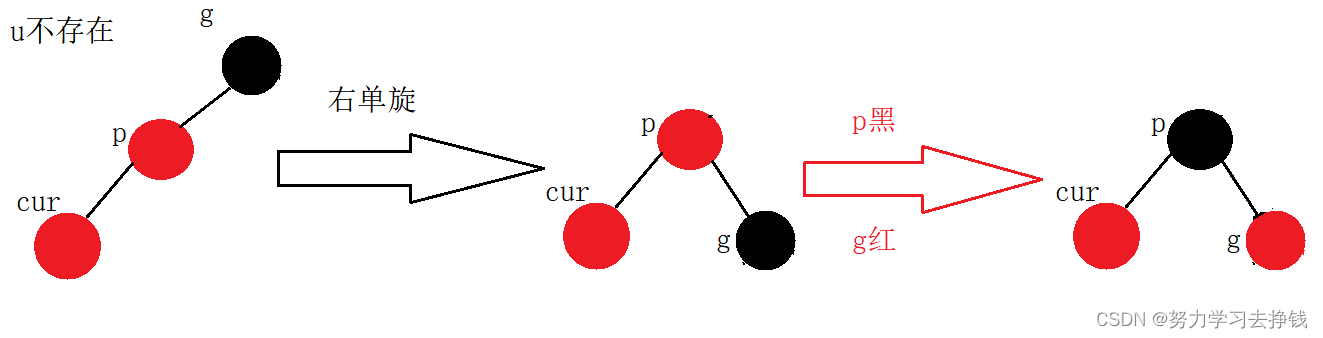
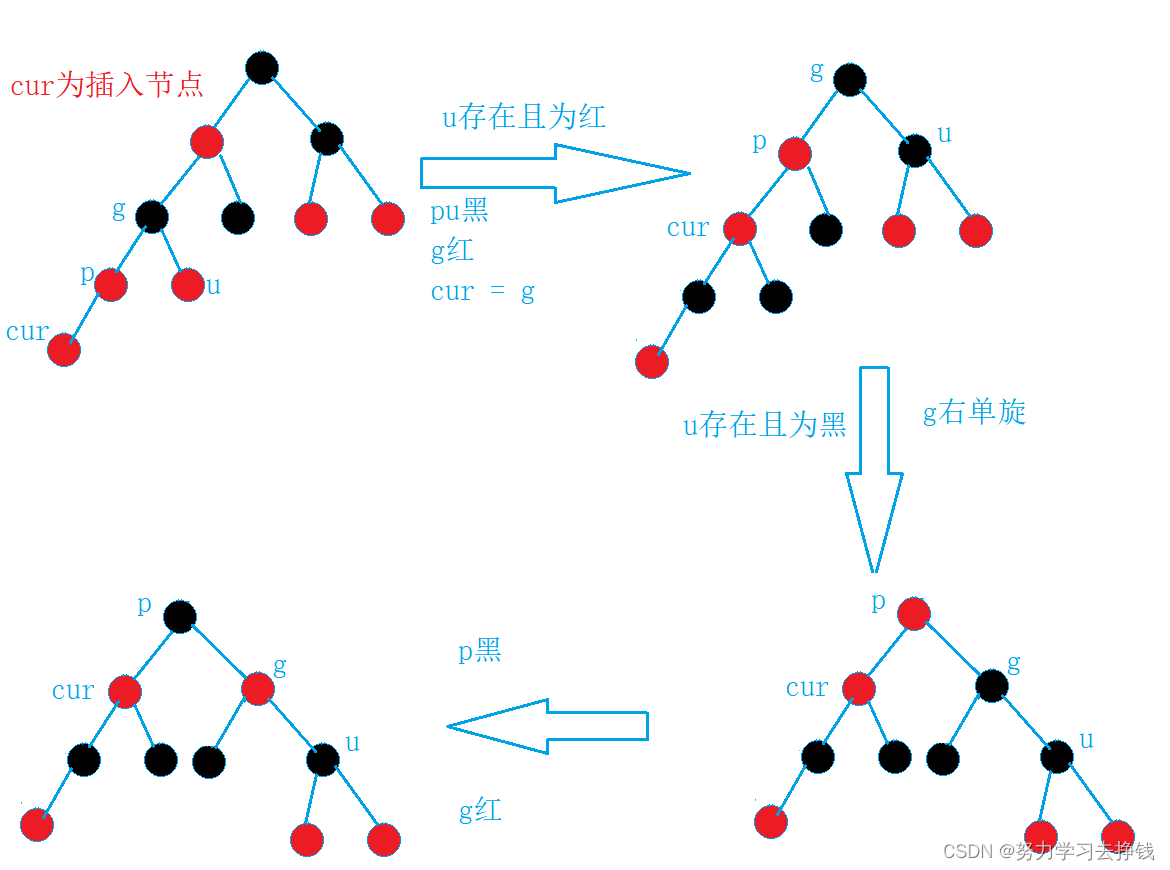
左左,右右:单旋 + 变色
单旋 + 变色。
和AVL树一样,左左就右单旋,右右就左单旋。
我就只画左左的,还是先给两个实例的图,再给抽象图。
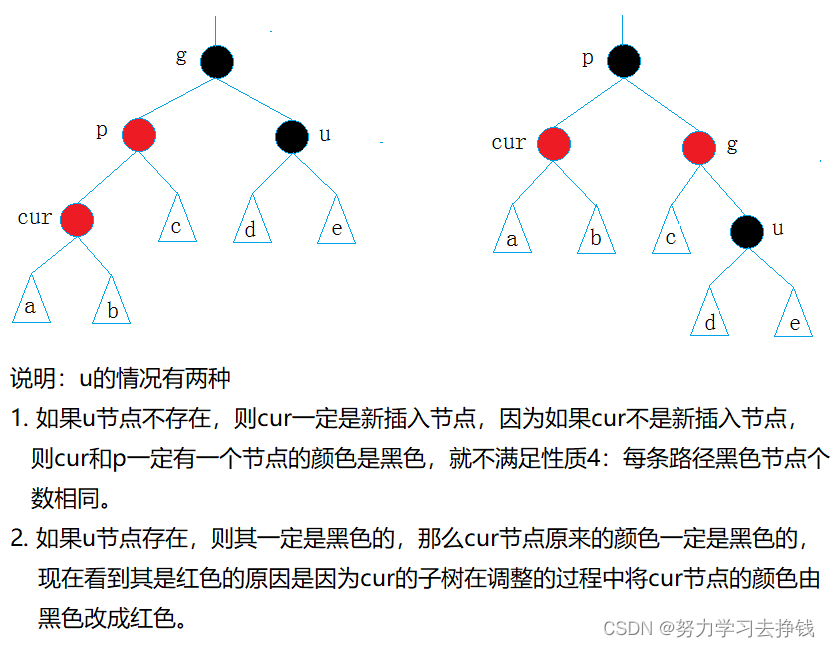
抽象图:
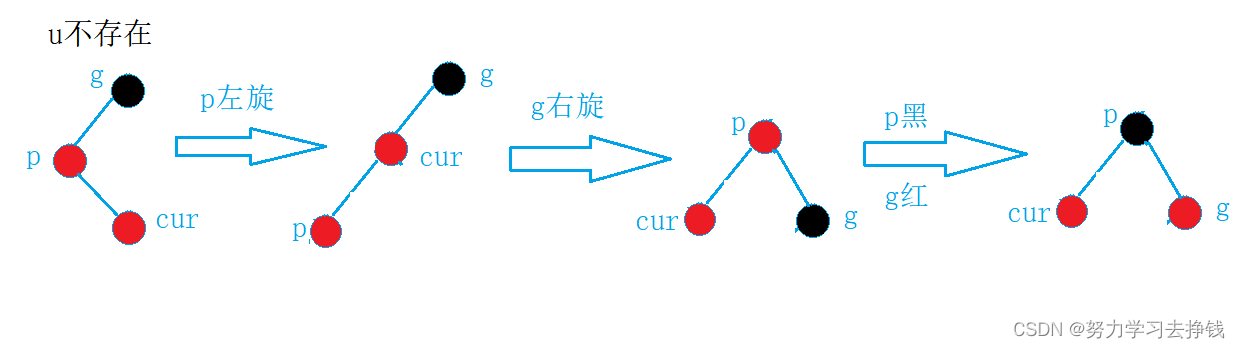
左右,右左:双旋 + 变色
单旋 + 变色。
和AVL树一样,左右就左右双旋,右左就右左双旋。
实例:
抽象图:
手画图:
总结一下:
红黑树调节平衡关键是看叔叔。
u存在且为红,变色继续往上处理。
u不存在 或者 存在且为黑,旋转+变色。其中旋转又分单旋和双旋,若p、cur在单侧,就单旋,若p、cur一左一右或一右一左就双旋。
上面的三种情况搞完就可以写代码了。
调节平衡的代码如下:

其中我光用了单旋,没有用双旋,因为双旋就是两个单旋。
单旋代码:

可以写一个中序遍历来简单打印一下结果:


但是简单的中序遍历可不够,来写一个专门用来检查是否平衡的函数。

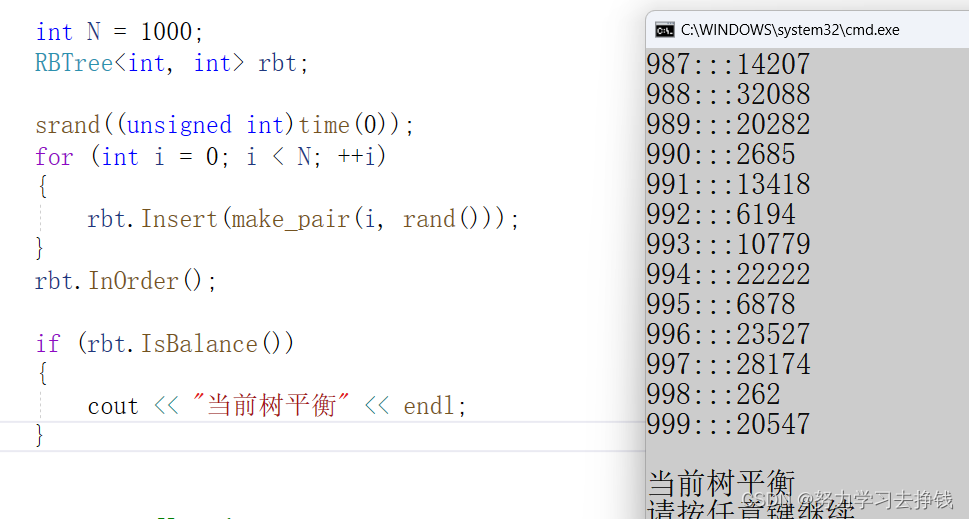
到此结束。。。
相关文章:

【C++】红黑树模拟实现插入功能(包含旋转和变色)
红黑树模拟实现并封装为map和set 前言正式开始红黑树概念红黑树基本要求大致框架树节点树 调整红黑树使其平衡第一种:cur红,p红,g黑,u存在且为红第二种:cur红,p红,g黑,u不存在或为黑…...
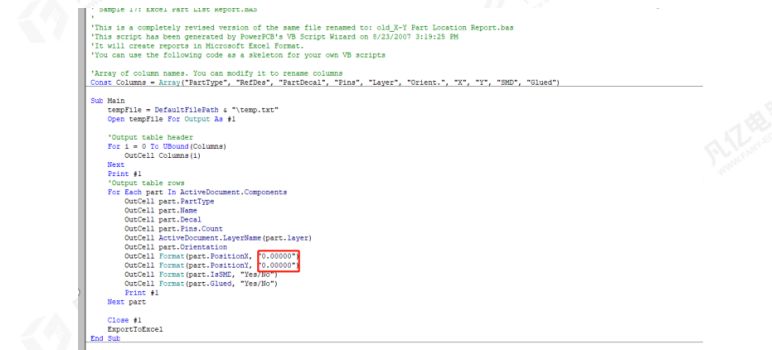
Pads输出器件坐标文件时,如何更改器件坐标精度
相信对于用pads软件的工程师么,在完成PCB设计的时候都需要输出生产文件给板厂和贴片厂,今天我们需要给大家介绍的是如何在在pads软件上面输出器件坐标文件以及如何更改器件坐标文件的精度。 首先我们需要点击工具-基本脚本-基本脚本接下来会跳到下面这个…...

Vuejs3父组传值给子组件
父组件代码 <script setup> import TextProps from ./components/TextProps.vue; import { reactive } from vue;const queryobj reactive({"a":1, "b":1}); const aryobj reactive([1,2,3]);</script><template><div class"…...

竞赛项目 深度学习的智能中文对话问答机器人
文章目录 0 简介1 项目架构2 项目的主要过程2.1 数据清洗、预处理2.2 分桶2.3 训练 3 项目的整体结构4 重要的API4.1 LSTM cells部分:4.2 损失函数:4.3 搭建seq2seq框架:4.4 测试部分:4.5 评价NLP测试效果:4.6 梯度截断…...

【剑指 の 精选】热门状态机 DP 运用题
题目描述 这是 LeetCode 上的 「剑指 Offer II 091. 粉刷房子」 ,难度为 「中等」。 Tag : 「状态机 DP」、「动态规划」 假如有一排房子,共 n 个,每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种,你需要粉刷所有的房子…...
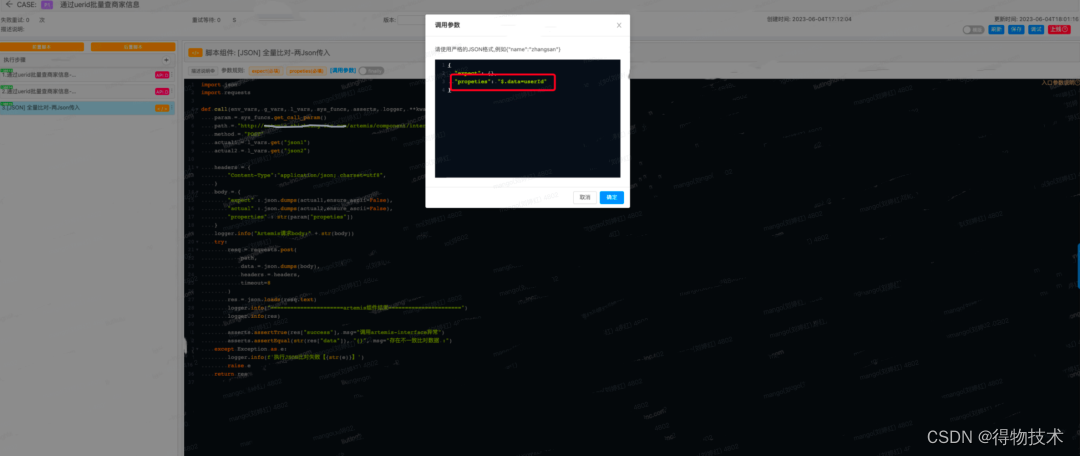
自动化实践-全量Json对比在技改需求提效实践
1 背景 随着自动化测试左移实践深入,越来越多不同类型的需求开始用自动化测试左移来实践,在实践的过程中也有了新的提效诉求,比如技改类的服务拆分项目或者BC流量拆分的项目,在实践过程中,这类需求会期望不同染色环境…...
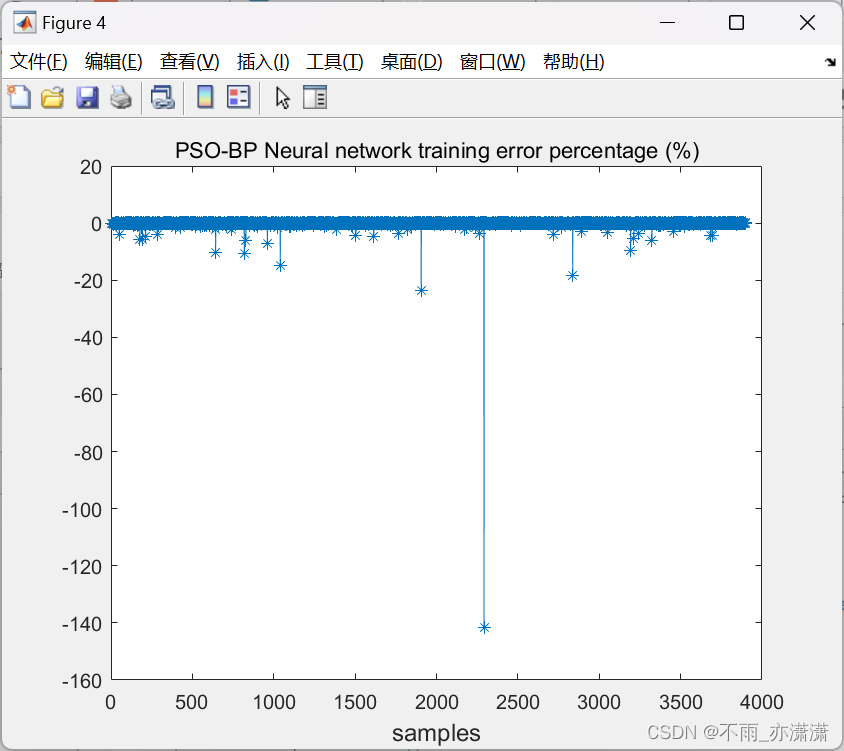
【Matlab】PSO优化(单隐层)BP神经网络
上一篇博客介绍了BP-GA:BP神经网络遗传算法(BP-GA)函数极值寻优——非线性函数求极值,本篇博客将介绍用PSO(粒子群优化算法)优化BP神经网络。 1.优化思路 BP神经网络的隐藏节点通常由重复的前向传递和反向传播的方式来决定&#…...

创建型模式-原型模式
文章目录 一、原型模式1. 概述2. 结构3. 实现4. 案例1.5 使用场景1.6 扩展(深克隆) 一、原型模式 1. 概述 用一个已经创建的实例作为原型,通过复制该原型对象来创建一个和原型对象相同的新对象。 2. 结构 原型模式包含如下角色: …...
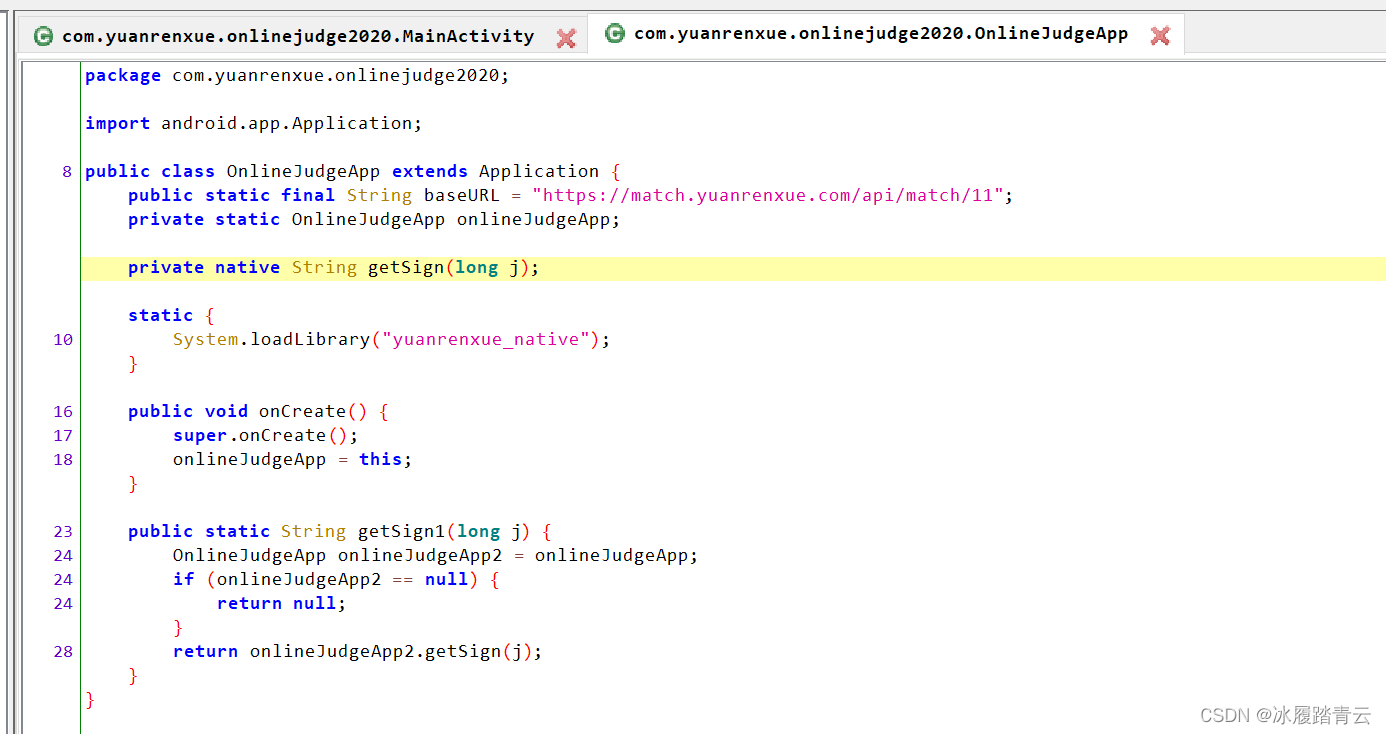
JS逆向系列之猿人学爬虫第11题 - app抓取 - so文件协议破解
题目地址 http://match.yuanrenxue.com/match/11这是个app题目,先下载下来安装到测试手机上 安装完成后的app界面长这样 打开之后是这样的: 要求已经简单明了了。 二话不说先反编译app 不出意外的是没出意外,源代码里面没啥混淆,所有东西都展示的明明白白的。 "…...
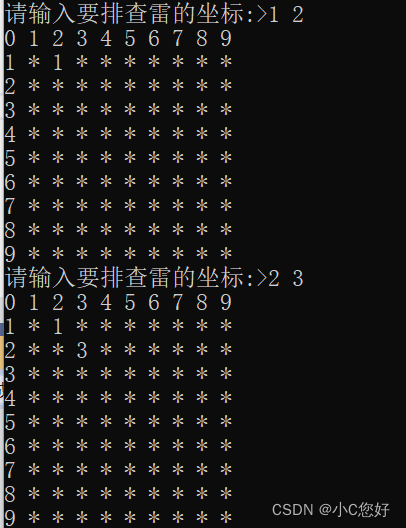
c基础扫雷
和三子棋一样,主函数先设计游戏菜单界面,这里就不做展示了。 初始化棋盘 初级扫雷大小为9*9的棋盘,但排雷是周围一圈进行排雷(8格),而边界可能会越界。数组扩大了一圈,行和列都加了2,所以我们用一个11*11的数组来初始化…...

端点中心(Endpoint Central)的软件许可证管理
软件许可证管理 (SLM) 是从单个控制台管理整个组织中使用的软件许可证的过程。软件许可证是由软件发行商或分销商制作的法律文件,提供有关软件使用和分发的规则和指南,本文档通常包含条款和条件、限制和免责声明。 软件许可证管理…...
SpringCloud源码探析(九)- Sentinel概念及使用
1.概述 在微服务的依赖调用中,若被调用方出现故障,出于自我保护的目的,调用方会主动停止调用,并根据业务需要进行对应处理,这种方式叫做熔断,是微服务的一种保护方式。为了保证服务的高可用性,…...
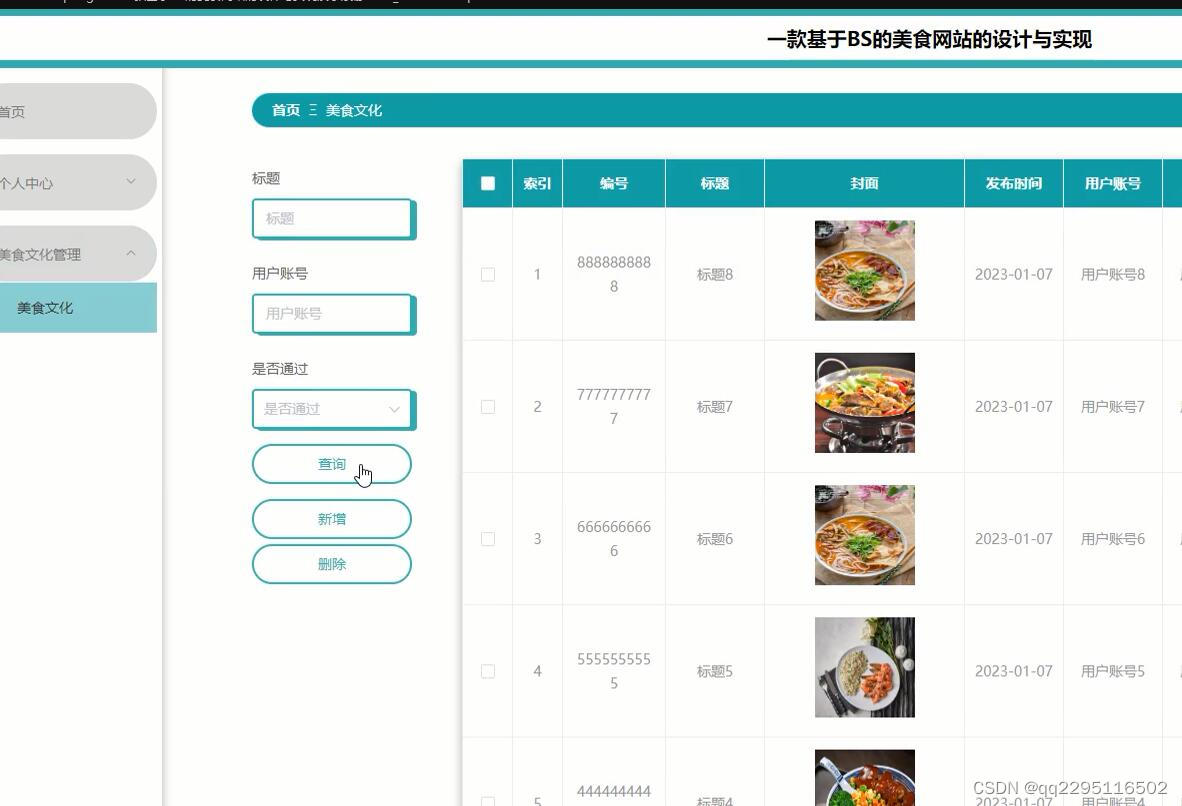
nodejs+vue+elementui美食网站的设计与实现演示录像2023_0fh04
本次的毕业设计主要就是设计并开发一个美食网站软件。运用当前Google提供的nodejs 框架来实现对美食信息查询功能。当然使用的数据库是mysql。系统主要包括个人信息修改,对餐厅管理、用户管理、餐厅信息管理、菜系分类管理、美食信息管理、美食文化管理、系统管理、…...

Mysql 数据库增删改查
MySQL是目前最流行的关系型数据库。以下是MySQL数据库的增删改查操作。 1.数据库连接 在进行增删改查操作之前,需要先连接MySQL数据库。使用以下命令进行连接: import mysql.connectormydb mysql.connector.connect(host"localhost",user&…...
【深度学习注意力机制系列】—— ECANet注意力机制(附pytorch实现)
ECANet(Efficient Channel Attention Network)是一种用于图像处理任务的神经网络架构,它在保持高效性的同时,有效地捕捉图像中的通道间关系,从而提升了特征表示的能力。ECANet通过引入通道注意力机制,以及在…...

python爬虫的简单实现
当涉及网络爬虫时,Python中最常用的库之一是requests。它能够发送HTTP请求并获取网页内容。下面是一个简单的示例,展示如何使用requests库来获取一个网页的内容: import requests 指定要爬取的网页的URL url ‘https://example.com’ 发…...

如何正确的向chatgpt提问?
有没有发现,在使用ChatGPT的时候,他回答的一些问题并不是我们想要的甚至有的时候出现牛头不对马嘴的情况。 这时候就会感慨一句,人工智能也不怎么样嘛! 但是,有没有想过,是自己问的问题太宽泛,没有问到点上…...
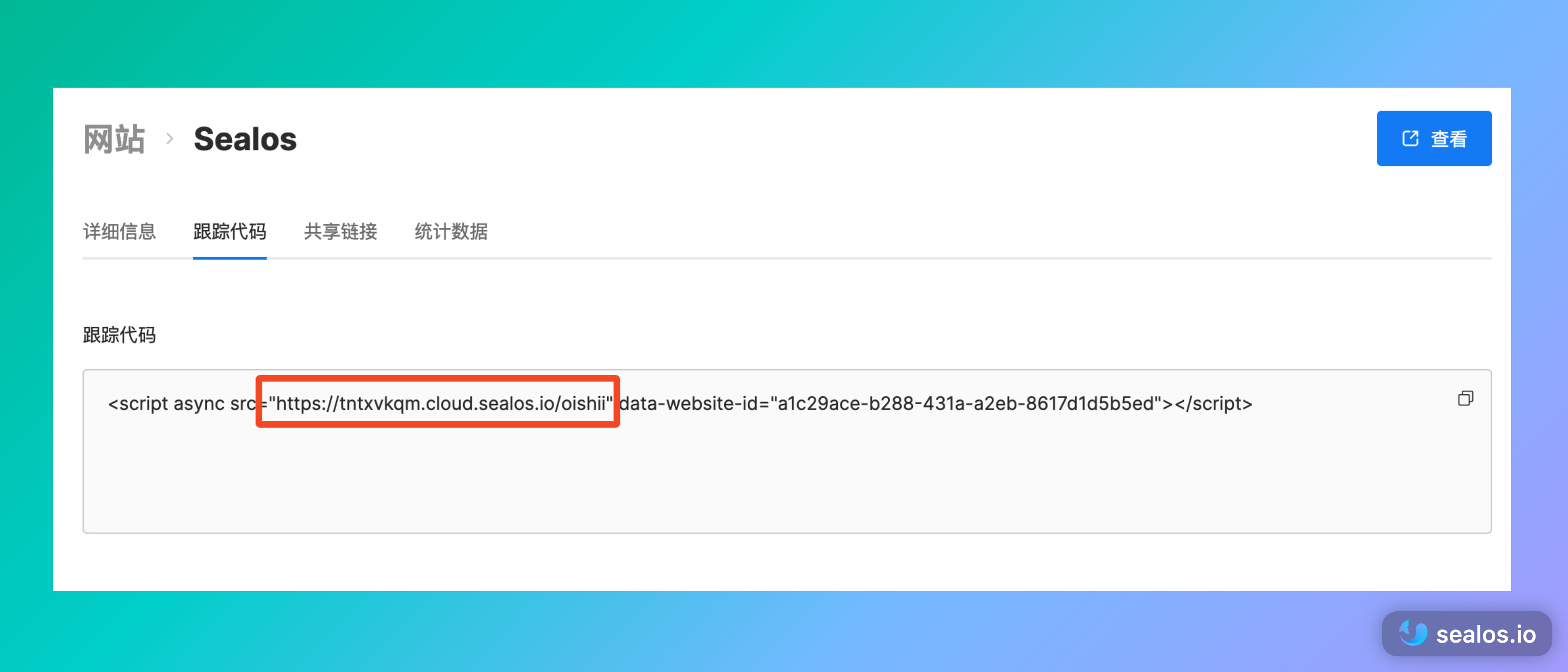
一键部署 Umami 统计个人网站访问数据
谈到网站统计,大家第一时间想到的肯定是 Google Analytics。然而,我们都知道 Google Analytics 会收集所有用户的信息,对数据没有任何控制和隐私保护。 Google Analytics 收集的指标实在是太多了,有很多都是不必要的,…...

java种的hutool库接口说明和整理
1. Hutool库基本介绍 1.1. 地址 官网地址:https://www.hutool.cn/ 1.2. 基本介绍 Hutool是一个小而全的Java工具类库,通过静态方法封装,降低相关API的学习成本,提高工作效率,使Java拥有函数式语言般的优雅…...

控制国外各类电液伺服阀放大器
控制通用型不带反馈信号输入的伺服阀放大器,对射流管式电液伺服阀、喷嘴挡板式电液伺服阀及国外各类电液伺服阀进行控制。 通过系统参数有10V和4~20mA输入指令信号选择; 供电电源: 24VDC(标准) 输出电流:最大可达10…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...