数据结构初阶--二叉树的链式结构
目录
一.二叉树链式结构的概念
二.二叉树链式结构的功能实现
2.1.链式二叉树的定义
2.2.链式二叉树的构建
2.3.链式二叉树的遍历
2.3.1.先序遍历
2.3.2.中序遍历
2.3.3.后序遍历
2.3.4.层序遍历
2.4.链式二叉树的求二叉树的结点数量
法一:计数法
法二:分治法
2.5.链式二叉树的求二叉树的叶子结点数量
2.6.链式二叉树的求二叉树第k层结点的数量
2.7.链式二叉树的求二叉树的高度
2.8.链式二叉树的查找二叉树中值为x的结点
2.9.链式二叉树的判断二叉树是否是完全二叉树
2.10.链式二叉树的二叉树的销毁
三.二叉树基础OJ练习
题一:单值二叉树
题二:相同的树
题三:对称二叉树
题四:另一棵树的子树
题五:二叉树的前序遍历
题六:二叉树遍历
前置说明:
在学习二叉树的基本操作之前,需要先创建一棵二叉树,然后才能学习其相关的基本操作。由于现在对于二叉树的结构掌握还不够深,为了降低大家的学习成本,此处手动创建一棵简单的二叉树,以便快速进入二叉树的操作学习。等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
一.二叉树链式结构的概念
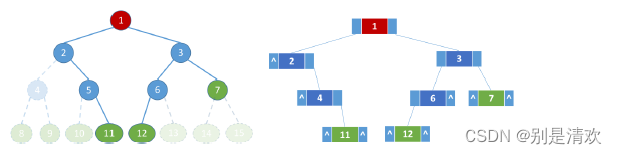
对于任意的二叉树来说,每个结点只有一个双亲结点(根除外),最多有两个孩子。可以设计每个结点至少包括三个域:数据域data,左孩子域left和右孩子域right。其中,left域指向该结点的左孩子,data域记录该结点的信息,right域指向该结点的右孩子。此结点结构形成的二叉树称为二叉链表。
二.二叉树链式结构的功能实现
若有n个结点,则有2n个指针域,而除了根结点每个结点头上都会连一个指针,故n个结点的二叉链表共有n+1个空链域。
2.1.链式二叉树的定义
typedef int BTDataType;typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;//左孩子指针struct BinaryTreeNode* right;//右孩子指针BTDataType data;//数据域
}BTNode;2.2.链式二叉树的构建
//创建结点
BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));assert(node);node->data = x;node->left = NULL;node->right = NULL;return node;
}//构造二叉树
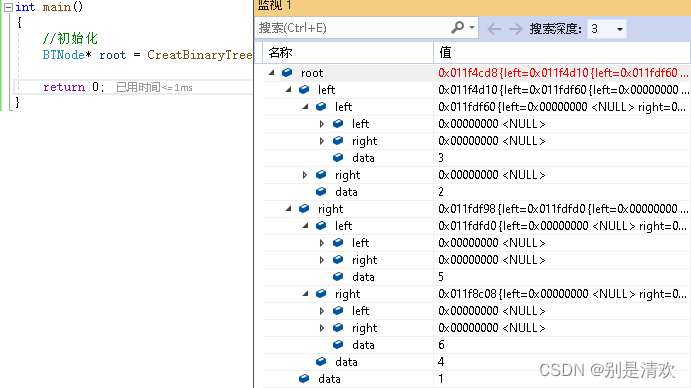
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}调试分析:
运行结果:
注意:
这种方式可以很简单地找到指定结点的左右孩子,但是要找到指定结点的父结点就只能从根结点开始遍历寻找。
2.3.链式二叉树的遍历
二叉树的遍历是指按一定规律对二叉树中的每个结点进行访问且仅访问一次。二叉树是非线性数据结构,通过遍历可以将二叉树中的结点访问一次且仅一次,从而得到访问结点的顺序序列。从这个意义上说,遍历操作就是将二叉树中结点按一定规律线性化的操作,目的在于将非线性化结构变成线性化的访问序列。
用L,D,R分别表示遍历左子树,访问根结点,遍历右子树。如果规定按先左后右的顺序,根据对根的访问先后顺序的不同,可以将DLR称为先序遍历或先根遍历,将LDR称为中序遍历,将LRD称为后序遍历。
注意:先序,中序和后序遍历都是递归定义的,即在其子树中亦按上述规律进行遍历。
案例分析:

2.3.1.先序遍历
若二叉树为空,则什么也不做;否则依次执行如下三个操作:
- 访问根结点;
- 先序遍历左子树;
- 先序遍历右子树。
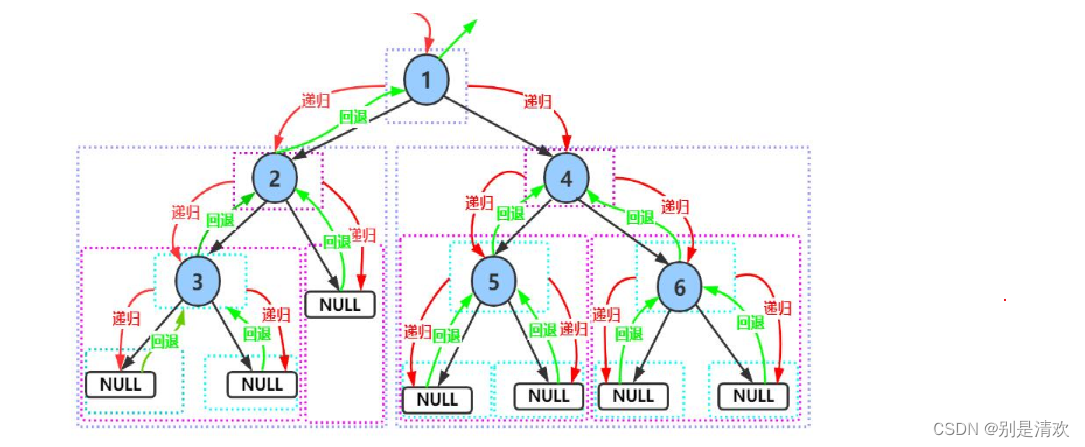
实现:
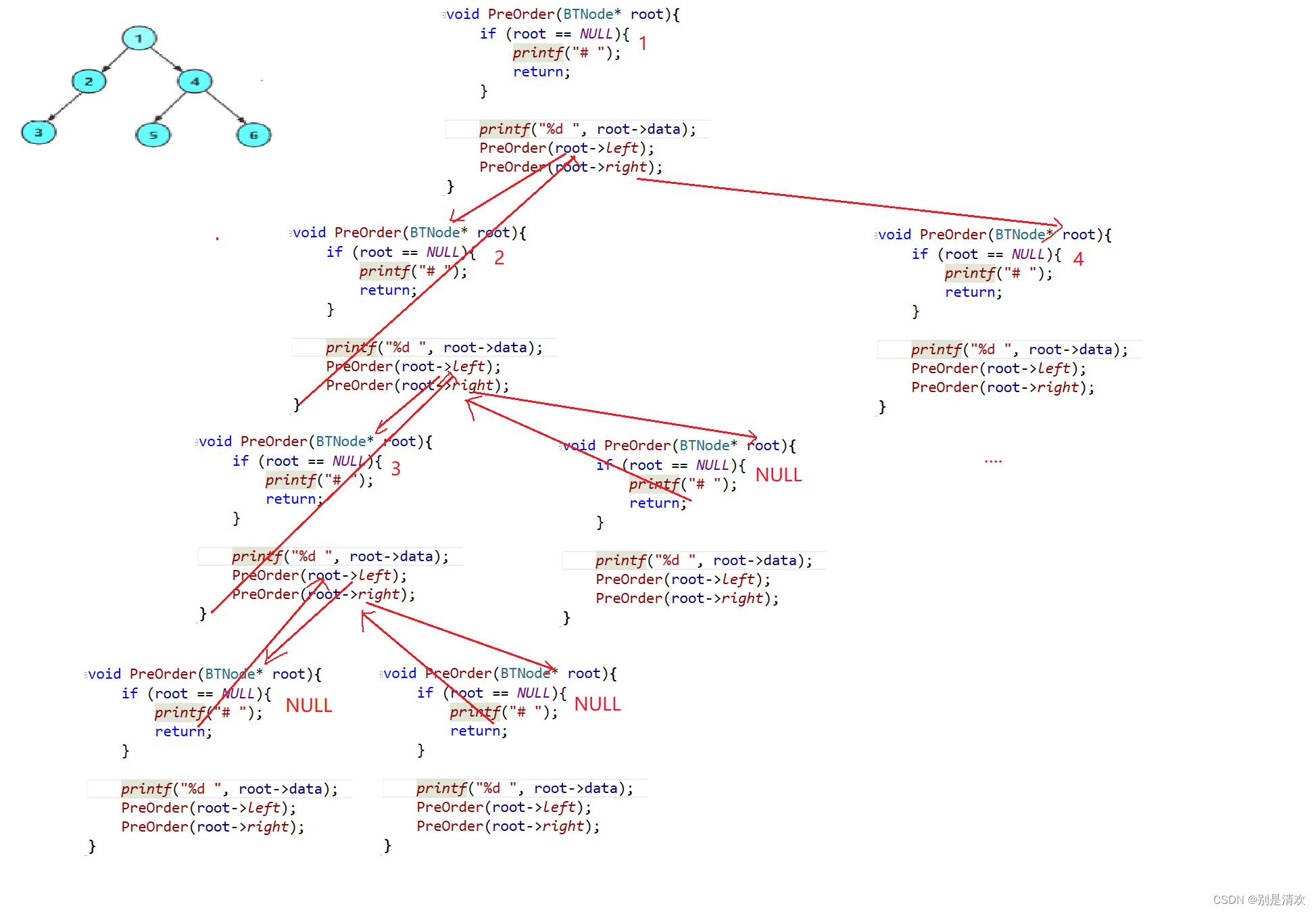
void PreOrder(BTNode* root)
{//若树为空,则退出if (root == NULL){printf("# ");//若结点为空,则用#表示return;}//先访问根结点printf("%d ", root->data);//然后访问左子树PreOrder(root->left);//再访问右子树PreOrder(root->right);
}运行结果:

递归分析:
2.3.2.中序遍历
若二叉树为空,则什么也不做;否则依次执行如下三个操作:
- 中序遍历左子树;
- 访问根结点;
- 中序遍历右子树。
实现:
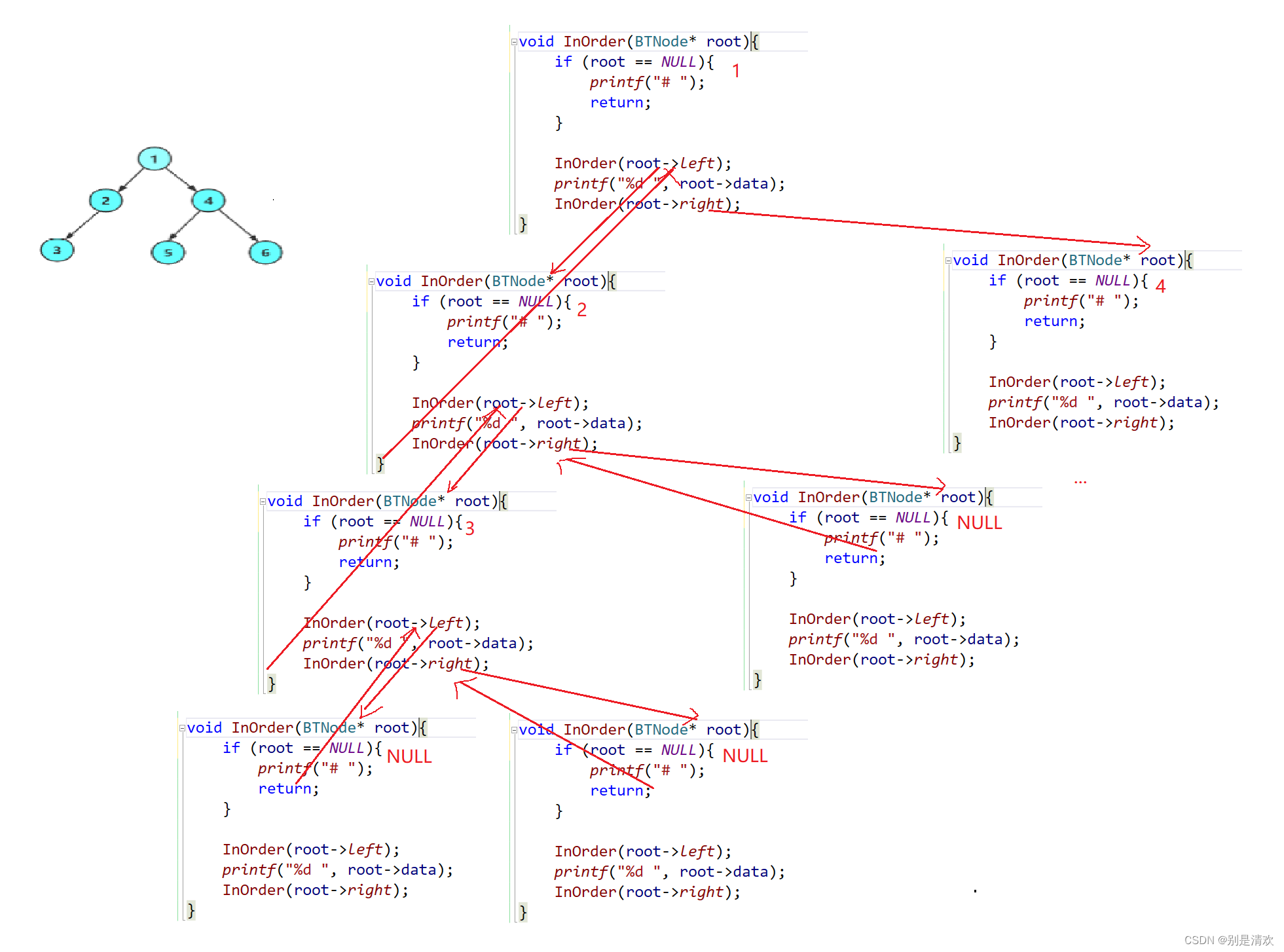
void InOrder(BTNode* root)
{//若树为空,则退出if (root == NULL){printf("# ");//若结点为空,则用#表示return;}//先访问左子树InOrder(root->left);//然后访问根结点printf("%d ",root->data);//再访问右子树InOrder(root->right);
}运行结果:
![]()
递归分析:
2.3.3.后序遍历
若二叉树为空,则什么也不做;否则依次执行如下三个操作:
- 后序遍历左子树;
- 后续遍历右子树;
- 访问根结点。
实现:
void PostOrder(BTNode* root)
{//若树为空,则退出if (root == NULL){printf("# ");//若结点为空,则用#表示return;}//先访问左子树PostOrder(root->left);//然后访问右子树PostOrder(root->right);//再访问根结点printf("%d ", root->data);
}运行结果:
![]()
小结:
递归算法的时间复杂度分析:设二叉树有n个结点,对每个结点都要进行一次入栈和出栈的操作,即入栈和出栈各执行n次,对结点的访问也是n次。这些二叉树递归遍历算法的时间复杂度为0(n)。
2.3.4.层序遍历
设二叉树的根结点所在层数为1,层序遍历就是从所在二叉树的根结点出发,首先访问第一层的树的根结点,然后从左到右访问第二层的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
实现方式:采用辅助队列实现按层序遍历二叉树。
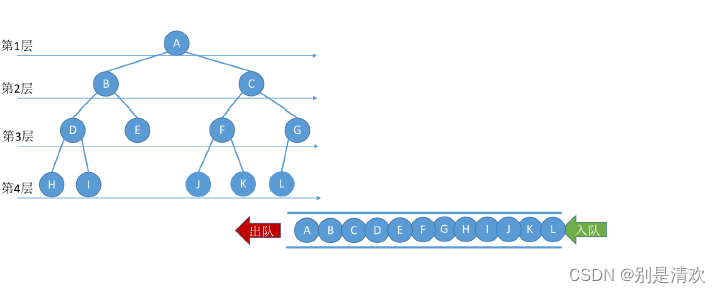
算法思想:
- 初始化一个辅助队列;
- 根结点入队;
- 若队列非空,则队头结点出队,访问该结点,并将其左,右孩子插入队尾(如果有的话);
- 重复第三步直至队列为空。
实现:
void LevelOrder(BTNode* root)
{//创建队列并初始化Queue q;QueueInit(&q);//若根结点不为空,则先将根结点入队if (root){//入队QueuePush(&q, root);}//若队列非空while (!QueueEmpty(&q)){//取队头元素BTNode* front = QueueFront(&q);//访问队头结点printf("%d ",front->data);//出队QueuePop(&q);//若左结点存在,则左结点入队if (front->left){//入队QueuePush(&q, front->left);}//若右节点存在,则右结点入队if (front->right){//入队QueuePush(&q, front->right);}}printf("\n");//销毁队列QueueDestory(&q);
}运行结果:
![]()
2.4.链式二叉树的求二叉树的结点数量
法一:计数法
在递归调用过程中,局部变量和全局变量的传递方式可以类似的看成函数调用时的值传递和引用传递。
局部变量:类似于值传递过程中的形参和实参,可以看成是两个完全不同的值,只是名字相同而已。每次递归调用时都会重新创建新的变量,它并不会覆盖掉上次递归调用过程中创建的值。
全局变量:类似于传地址过程中的形参和实参,可以看成是同一个变量。每次递归调用时并不会重新创建新的变量,在递归过程中对全局变量的修改,会影响到下一次递归调用过程中的值。
所以,我们在使用计数器进行结点个数统计是,要定义全局变量而非局部变量。
当使用局部变量时:
int TreeSize(BTNode* root)
{int count = 0;//若树为空if (root == NULL){return;}//统计根结点++count;//统计左子树TreeSize(root->left);//统计右子树TreeSize(root->right);return count;
}运行结果:
![]()
当使用全局变量时:
int count = 0;//不能定义一个局部变量,因为每次递归调用都会重新初始化为0void TreeSize(BTNode* root)
{//若树为空if (root == NULL){return;}//统计根结点++count;//统计左子树TreeSize(root->left);//统计右子树TreeSize(root->right);}
运行结果:
![]()
这里存在一个问题:当我们多次打印输出结果时,可以发现每次的输出结果并不相同。如下所示:

为了避免该类问题的出现,只需在每次调用之前要将count进行初始化,防止下次调用时将前一次的调用结果进行累加。如下所示:

法二:分治法
使用计数法计算结点个数时存在较多需要注意的问题,而使用分治法可以有效解决此类问题。
采用递归算法,首先判断树是否为空树,若为空树,则返回0;若不是空树,则将根结点root的左孩子结点和右孩子结点作为参数传给函数TreeSize进行递归调用。
实现:
int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}递归分析:
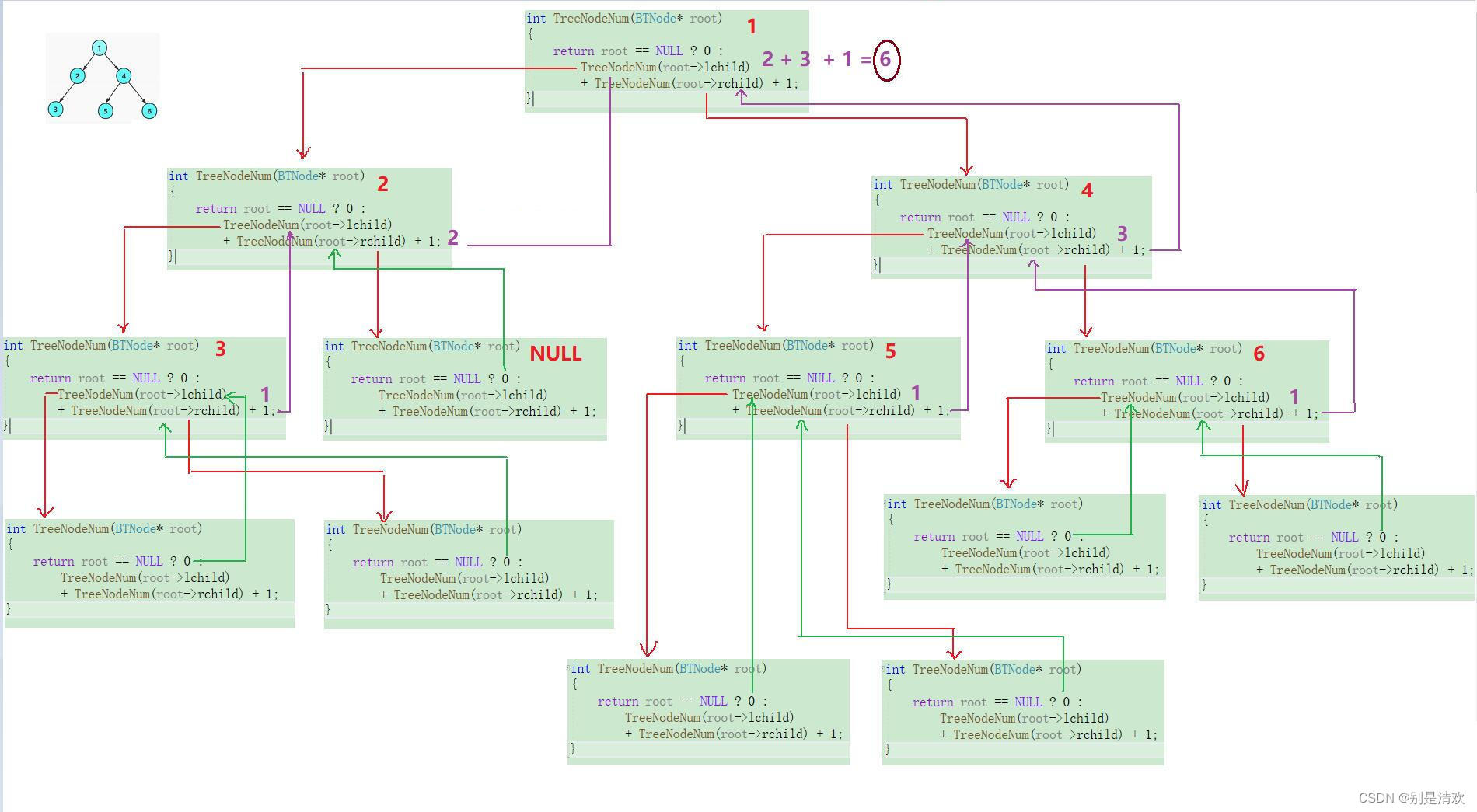
运行结果:
![]()
2.5.链式二叉树的求二叉树的叶子结点数量
采用递归算法,如果是空树,返回0;如果只有一个结点,返回1;否则为左右子树的叶子结点数之和。
实现:
int TreeLeafSize(BTNode* root)
{//若树为空if (root == NULL){return 0;}//若为单独的叶子,即只含一个结点if (root->left == NULL && root->right == NULL) {return 1;}//若树不为空,也不为单独的叶子return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}运行结果:
![]()
2.6.链式二叉树的求二叉树第k层结点的数量
采用递归算法,首先判断k的取值是否合法,k的取值不能小于1,然后判断树是否为空,如果是空树,则返回0;如果树不为空,且k的值为1,则返回1;否则为左右子树的第k-1层的结点数之和。
实现:
int TreeKLevel(BTNode* root, int k)
{//检查k的范围assert(k >= 1);//若树为空if (root == NULL){return 0;}//若树不为空,且k等于1,也就是根结点所在层次if (k == 1){return 1;}//求左子树和右子树的第k-1层的结点数之和return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}
递归分析:
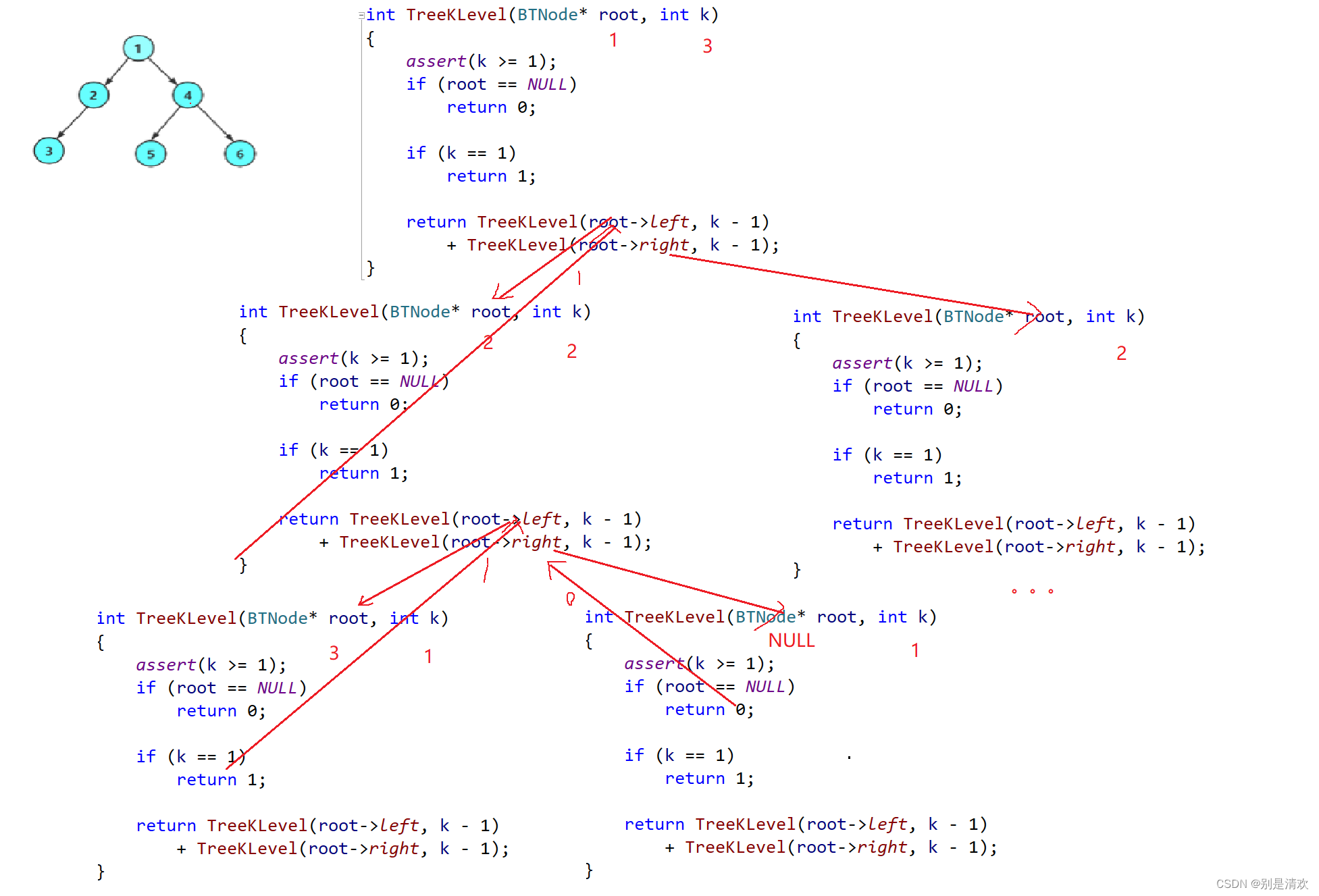
运行结果:
![]()
2.7.链式二叉树的求二叉树的高度
采用递归算法,首先判断树是否为空,若为空,则返回0;若不为空,则递归求左子树的高度和右子树的高度,然后再求出左子树和右子树高度的较大值,最后再将高度的最大值+1,即为所求二叉树的高度。
实现:
int TreeDepth(BTNode* root)
{//若树为空if (root == NULL){return 0;}//求左树的高度int leftDepth = TreeDepth(root->left);//求右树的高度int rightDepth = TreeDepth(root->right);//求两者中较大值return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}运行结果:
![]()
2.8.链式二叉树的查找二叉树中值为x的结点
采用递归算法,首先判断树是否为空,若树为空,则返回NULL。当树不为空,且根结点为所要查找的结点时,则返回根结点。否则,递归遍历左子树和右子树。
实现:
BTNode* TreeFind(BTNode* root, BTDataType x)
{//若树为空if (root == NULL){return NULL;}//若根结点为所要查找的结点if (root->data == x){return root;}//查找左子树BTNode* ret1 = TreeFind(root->left, x);//若返回值不为空if (ret1){return ret1;}//查找右子树BTNode* ret2 = TreeFind(root->right, x);//若返回值不为空if (ret2){return ret2;}return NULL;
}递归分析:
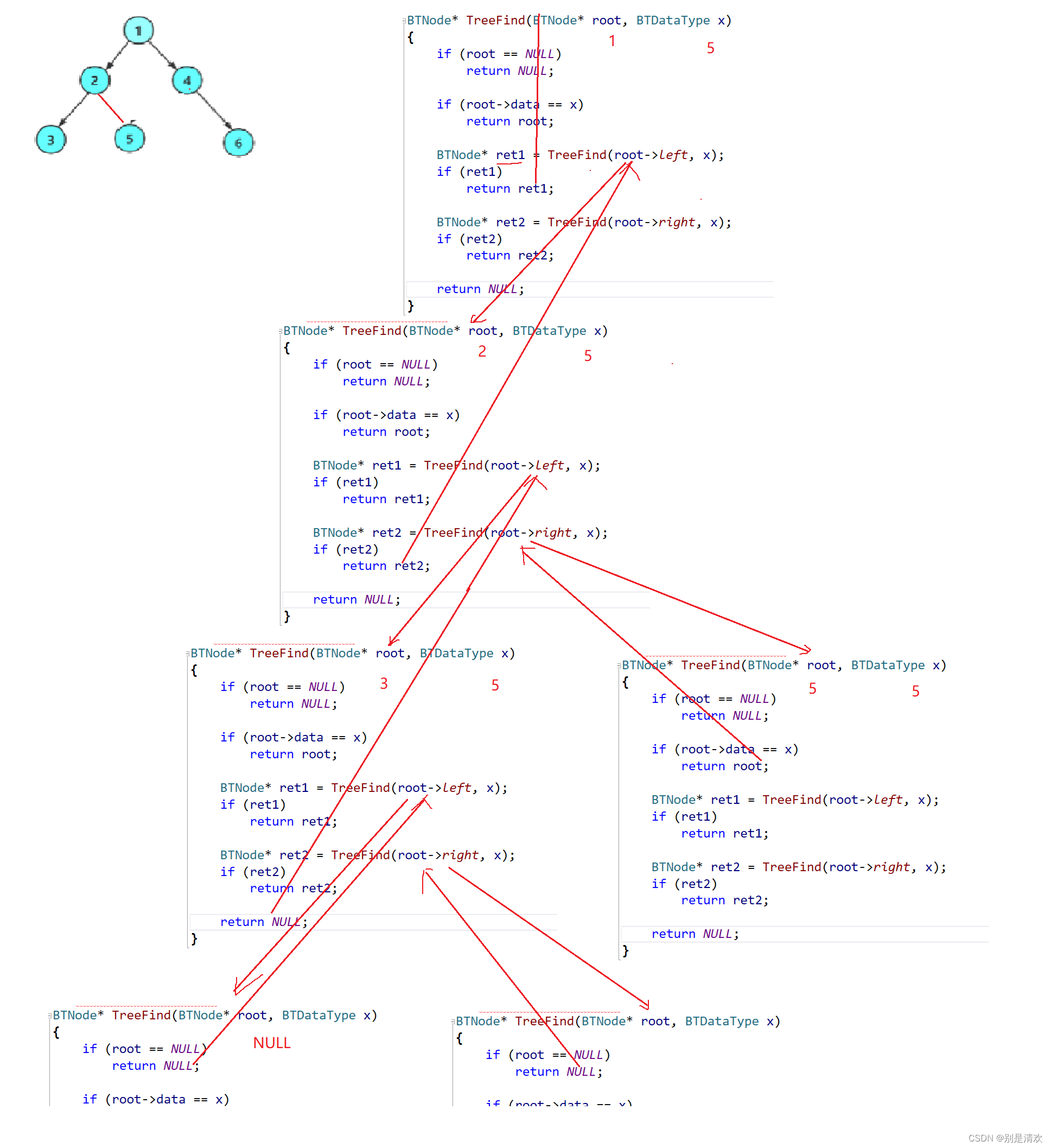
运行结果:

2.9.链式二叉树的判断二叉树是否是完全二叉树
完全二叉树:对于一棵深度为h的二叉树,其前h-1层结点个数均达到最大值,第h层结点个数可能没有达到最大值,但从左到右是连续的。
算法思想:
- 初始化一个辅助队列;
- 根结点入队;
- 若队列非空,则队头结点出队,访问该结点,并将其左,右孩子插入队尾(包含空结点);
- 重复第三步直至遇到空结点,并查看其后续是否有非空结点。若有,则该二叉树不是完全二叉树;若没有,则该二叉树是完全二叉树。
实现:
int TreeComplete(BTNode* root)
{//初始化队列Queue q;QueueInit(&q);//先将根结点入队if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){//读取队头元素并出队BTNode* front = QueueFront(&q);QueuePop(&q);//若队头结点非空if (front){//左结点入队,包含空结点QueuePush(&q, front->left);//右结点入队,包含空结点QueuePush(&q, front->right);}else{//遇到空,则跳出层序遍历break;}}//1.如果空后面全是空结点,则是完全二叉树//2.如果空后面还有非空结点,则不是完全二叉树while (!QueueEmpty(&q)){//读取队头元素并出队BTNode* front = QueueFront(&q);QueuePop(&q);//front存放的是树的结点的指针if (front){QueueDestory(&q);return false;}}//销毁QueueDestory(&q);return true;
}运行结果:
![]()
2.10.链式二叉树的二叉树的销毁
采用递归算法,首先判断树是否为空,若为空,则返回NULL。若树不为空,则先递归销毁左子树,然后再销毁右子树,最后再释放根结点。
实现:
void TreeDestroy(BTNode* root)
{//若树为空if (root == NULL){return;}//销毁左子树TreeDestroy(root->left);//销毁右子树TreeDestroy(root->right);printf("%p:%d\n", root, root->data);//释放根结点free(root);
}
运行结果:

三.二叉树基础OJ练习
题一:单值二叉树
题目描述:
如果二叉树每个结点都具有相同的值,那么该二叉树就是单值二叉树。只有给定的树是单值二叉树,才返回true;否则返回false。
法一:标记法
设置标志位flag进行单值二叉树的判断。若树为空或者标志位flag为flase,则直接返回;若根结点的值不等于val,则将标志位flag设为flase,同时返回;若上述两个条件均满足,则递归遍历左子树和右子树。
实现:
struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};//法一:设置标记位
bool flag = true;
void PreOrderCompare(struct TreeNode* root, int val)
{//若树为空if (root == NULL || flag == false)//flag==flase:若左子树不满足条件则直接退出,以免对右子树进行不必要的递归遍历{return;}//如果根结点的值不等于val,则直接退出,不用往下递归if (root->val != val){flag = false;return;}//比较左子树PreOrderCompare(root->left, val);//比较右子树PreOrderCompare(root->right,val);
}bool isUnivalTree(struct TreeNode* root)
{//若树为空if (root == NULL){return true;}flag = true;PreOrderCompare(root, root->val);return flag;
}法二:
首先判断根结点root是否为NULL,若为空则直接返回true。然后判断根结点root的左孩子与右孩子是否为空且其值与root的值是否相同,若不同,则返回false;若相同,则直接递归遍历root的左子树和右子树,判断其否为单值二叉树。
实现:
struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};bool isUnivalTree(struct TreeNode* root)
{//如果树为空if (root == NULL){return true;}//若左孩子不为空且左孩子的值不等于根结点if (root->left && root->left->val != root->val){return false;}//若右孩子不为空且右孩子的值不等于根结点if (root->right && root->right->val != root->val){return false;}//递归遍历左子树和右子树return isUnivalTree(root->left) && isUnivalTree(root->right);//递归调用的返回,都是返回到递归调用的上一层
}
递归分析:
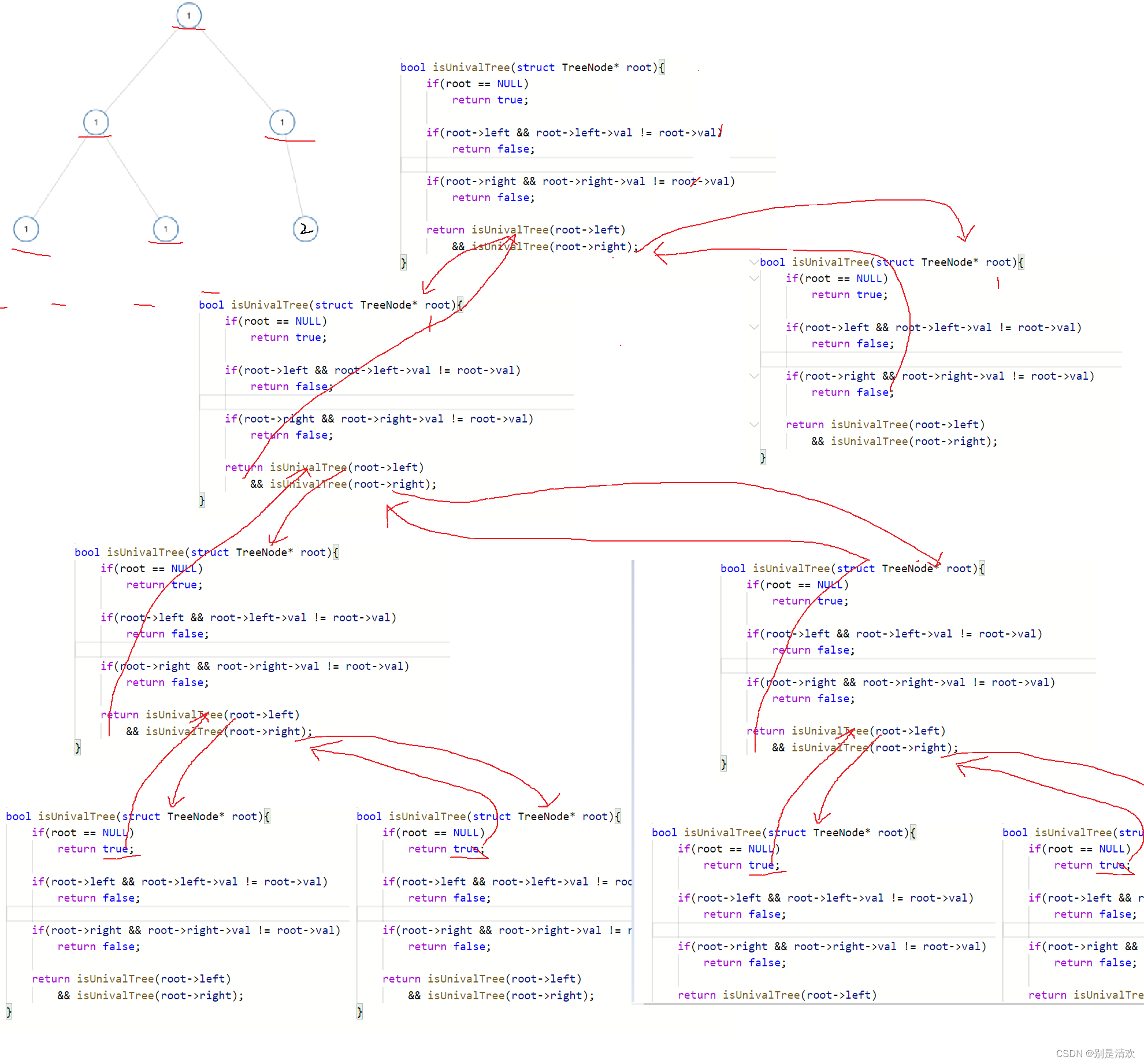
题二:相同的树
题目描述:
给你两棵二叉树的根结点p和q,编写一个函数来检验这两棵树是否相同。如果两棵树在结构上相同,并且结点具有相同的值,则认为它们是相同的。
分析:
首先判断两棵树是否均为空,若均为空,则返回true;若有一棵树为空,则返回false。然后在两棵树均不为空的情况下,判断其对应的根结点的值是否相等,若不相等则返回false。最后再递归遍历两棵树对应的左子树和右子树,判断其对应的结点值是否相等。
实现:
struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{//如果两棵树都为空if (p == NULL && q == NULL){return true;}//如果两棵树有一棵为空if (p == NULL || q == NULL){return false;}//如果两棵子树都不为空,且两个根结点的值不相等if (p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}题三:对称二叉树
题目描述:
给你一个二叉树的根结点root,检查它是否轴对称。
分析:
首先判断树是否为空,若为空则返回true,若不唯空,则判断根结点root对应的左子树和右子树。然后转为对左子树和右子树的判断,若两棵子树均为空,咋返回true;若有一棵子树为空,则返回false;若两棵子树均不为空,且其对应的根结点的值不相等,则返回false。最后再递归遍历,判断左子树的左子树与右子树的右子树以及左子树的右子树与右子树的左子树是否相等。
实现:
struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};bool isSymmetricSubTree(struct TreeNode* root1, struct TreeNode* root2)
{//若两棵树均为空if (root1 == NULL && root2 == NULL){return true;}//若有一棵树为空if (root1 == NULL || root2 == NULL){return false;}//若两棵树均不为空if (root1->val != root2->val){return false;}return isSymmetricSubTree(root1->left, root2->right) && isSymmetricSubTree(root1->right, root2->left);
}bool isSymmetric(struct TreeNode* root)
{//若树为空if (root == NULL){return true;}//若树不为空return isSymmetricSubTree(root->left, root->right);
}题四:另一棵树的子树
题目描述:
给你两棵二叉树root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在,返回true;否则,返回false。
二叉树tree的一棵子树包括tree的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。
分析:
遍历二叉树root中的每一个结点,然后将每一个结点都作为根结点并与subRoot的根结点进行比较,若对应的根结点值相同,则调用函数isSameTree进行左右子树的比较。如果左右子树均相同,则subRoot是root的子树;否则继续将二叉树root的下一个结点与subRoot的根结点进行比较。重复上述操作,直至找到一棵子树与二叉树subRoot相同或者二叉树root的所有子树均与subRoot不同并退出。
实现:
struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{//如果两棵树都为空if (p == NULL && q == NULL){return true;}//如果两棵树有一棵为空if (p == NULL || q == NULL){return false;}//如果两棵子树都不为空,且两个根结点的值不相等if (p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{//若树为空if (root == NULL)return false;//若树不为空if (isSameTree(root, subRoot)){return true;}//将原树中所有子树都找出来,然后跟subRoot比较return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}递归分析:
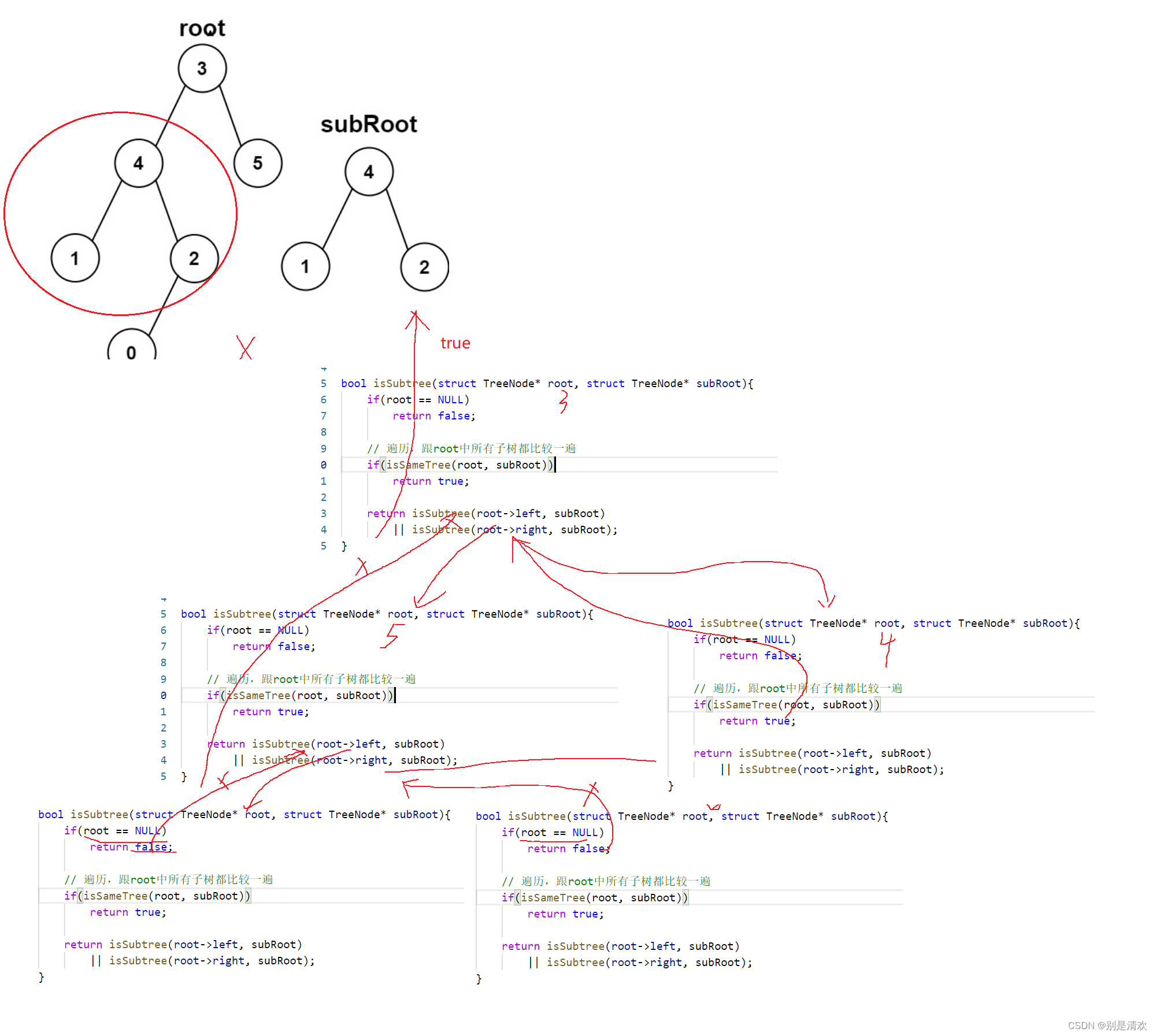
题五:二叉树的前序遍历
题目描述:
给你二叉树的根结点root,返回它结点值的前序遍历。
分析:
实现函数TreeSize,用以统计二叉树中的结点个数并返回给returnSize。同时开辟好returnSize个int 类型大小的数组空间,用于存放遍历后的各个结点。最后再调用函数preorder进行先序遍历,并返回数组首元素的地址。
实现:
struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;
};//求二叉树的结点个数
int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}//前序遍历,并将遍历后的结点值存入数组中
void preorder(struct TreeNode* root, int* a, int* pi)//pi的值要加引用,否则形参的修改不会影响实参
{//如果树为空if (root == NULL){return;}//若树不为空a[(*pi)++] = root->val;//遍历左子树preorder(root->left, a, pi);//遍历右子树preorder(root->right, a, pi);
}int* preorderTraversal(struct TreeNode* root, int* returnSize)
{//*returnSize用于接收二叉树的节点个数*returnSize = TreeSize(root);//开辟*returnSize个int类型大小的空间用于存放遍历后的结点int* a = (int*)malloc(*returnSize * sizeof(int));//进行前序遍历int i = 0;preorder(root, a, &i);return a;
}题六:二叉树遍历
题目描述:
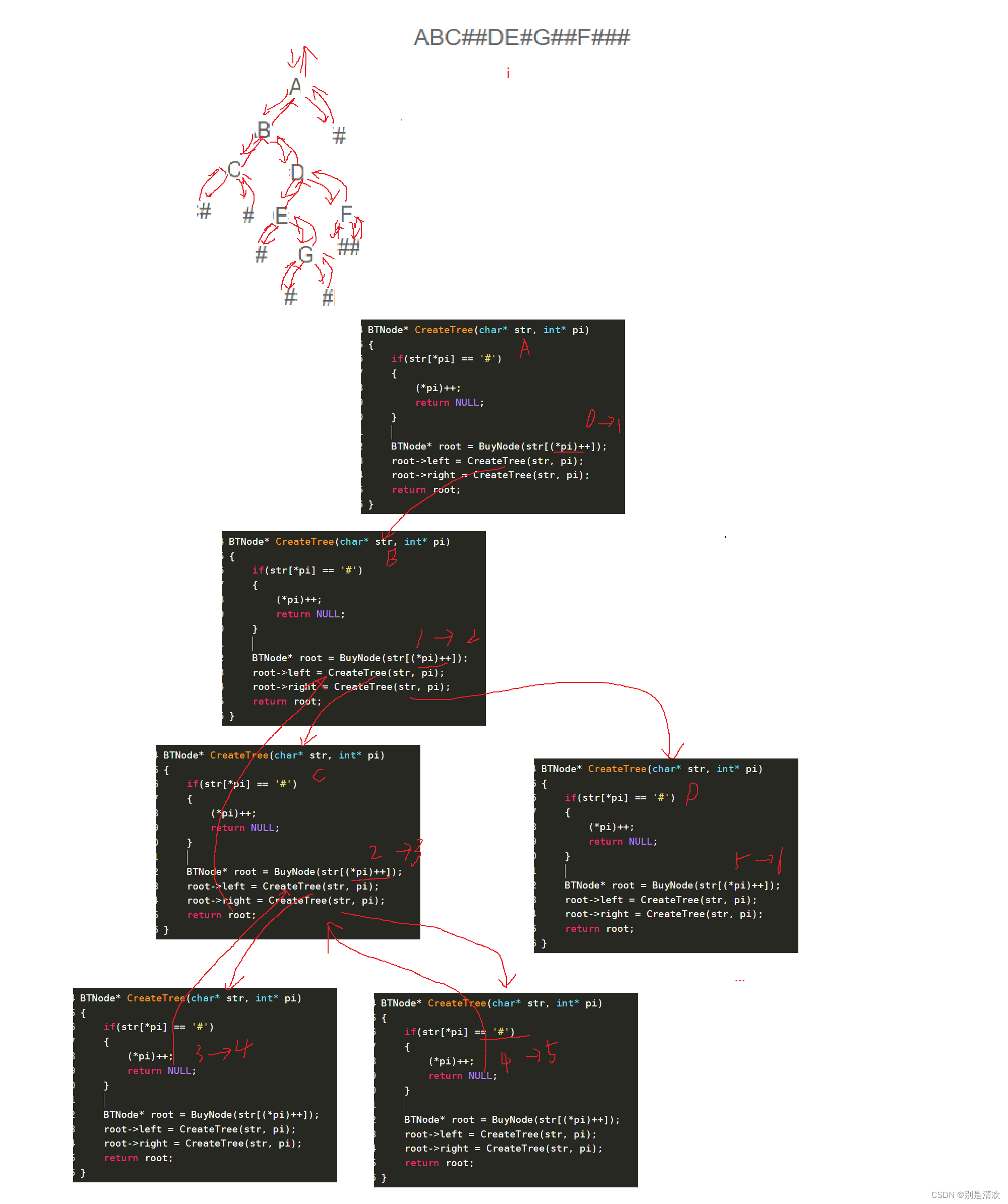
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。例如如下的先序遍历字符串:ABC##DE#G##F###其中"#"表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
分析:
根据所给的先序遍历字符串,采用前序遍历的方式进行二叉树的创建,再将创建好的二叉树进行中序遍历即可。
实现:
//二叉树的定义
typedef char BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;//左子树struct BinaryTreeNode* right;//右子树BTDataType data;
}BTNode;//创建结点
BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));assert(node);node->data = x;node->left = NULL;node->right = NULL;return node;
}//前序创建二叉树
BTNode* CreateTree(char* str, int* pi)
{//若结点为空,也就是空树,空树数组的下标也要++,且为它malloc空间进行存储if (str[*pi] == '#'){(*pi)++;return NULL;}//前序构建二叉树BTNode* root = BuyNode(str[(*pi)++]);root->left = CreateTree(str, pi);root->right = CreateTree(str, pi);return root;
}//中序遍历二叉树
void InOrder(BTNode* root)
{//判断树是否为空if (root == NULL){return;}InOrder(root->left);printf("%c ",root->data);InOrder(root->right);
}int main()
{char str[100];scanf("%s", str);int i = 0;BTNode* root = CreateTree(str, &i);InOrder(root);return 0;
}递归分析:
相关文章:

数据结构初阶--二叉树的链式结构
目录 一.二叉树链式结构的概念 二.二叉树链式结构的功能实现 2.1.链式二叉树的定义 2.2.链式二叉树的构建 2.3.链式二叉树的遍历 2.3.1.先序遍历 2.3.2.中序遍历 2.3.3.后序遍历 2.3.4.层序遍历 2.4.链式二叉树的求二叉树的结点数量 法一:计数法 法二&a…...

Taro UI中的AtTabs
TaroUI 中的 AtTabs 是一个用于创建标签页(tab)组件的组件。它提供了一种简单的方式来切换显示不同的内容。 AtTabs 的使用方式如下: 首先,引入 AtTabs 组件和必要的样式: import { AtTabs, AtTabsPane } from taro-ui import taro-ui/dis…...

ChatGPT FAQ指南
问:chatgpt 国内不开放注册吗? OpenAI不允许大陆和香港用户注册访问 openai可以的,chatGPT不行 以下国家IP不支持使用 中国(包含港澳台) 俄罗斯 乌克兰 阿富汗 白俄罗斯 委内瑞拉 伊朗 埃及 问:ChatGPT和GPT-3什么关系? GPT-3是OpenAI推出的AI大语言模型 ChatGPT是在G…...

在矩池云使用ChatGLM-6B ChatGLM2-6B
ChatGLM-6B 和 ChatGLM2-6B都是基于 General Language Model (GLM) 架构的对话语言模型,是清华大学 KEG 实验室和智谱 AI 公司于 2023 年共同发布的语言模型。模型有 62 亿参数,一经发布便受到了开源社区的欢迎,在中文语义理解和对话生成上有…...
7.2 手撕VGG11模型 使用Fashion_mnist数据训练VGG
VGG首先引入块的思想将模型通用模板化 VGG模型的特点 与AlexNet,LeNet一样,VGG网络可以分为两部分,第一部分主要由卷积层和汇聚层组成,第二部分由全连接层组成。 VGG有5个卷积块,前两个块包含一个卷积层,…...

docker安装ES
拉取镜像文件 sudo docker pull elasticsearch:7.12.0 创建容器挂载目录 sudo mkdir -p /home/elasticsearch/config sudo mkdir -p /home/elasticsearch/data sudo mkdir -p /home/elasticsearch/plugins elasticsearch.yml http.host: 0.0.0.0 创建容器 sudo docker r…...
python爬虫实战(2)--爬取某博热搜数据
1. 准备工作 使用python语言可以快速实现,调用BeautifulSoup包里面的方法 安装BeautifulSoup pip install BeautifulSoup完成以后引入项目 2. 开发 定义url url https://s.微博.com/top/summary?caterealtimehot定义请求头,微博请求数据需要cookie…...

k8s的Namespace详解
简介 在一个K8s集群中可以拥有多个命名空间,它们在逻辑上彼此隔离 namespaces是对一组资源和对象的抽象集合,比如可以将系统内部的对象划分为不同的项目组或用户组 K8s在集群启动之后,会默认创建几个namespace默认namespace defaultÿ…...

【Redis】Redis内存过期策略和内存淘汰策略
【Redis】Redis内存过期策略和内存淘汰策略 文章目录 【Redis】Redis内存过期策略和内存淘汰策略1. 过期策略1.1 惰性删除1.2 周期删除1.2.1 SLOW模式1.2.2 FAST模式 2. 淘汰策略 1. 过期策略 Redis本身是一个典型的key-value内存存储数据库,因此所有的key、value都…...

技术干货 | cilium 原理之sock_connect
1.背景 在集群网络使用cilium之后,最明显的情况就是:服务暴露vipport,在集群内怎么测试都正常,但集群外访问可能是有问题的。而这就在于cilium所使用的ebpf科技。 2.引子:curl请求的路程 相对底层一点的语言…...

K8S之Pod详解与进阶
Pod详解与进阶 文章目录 Pod详解与进阶一、Pod详解1.pod定义2.pause容器作用3.Pod 的 3 种类型4.Pod 的 3 种容器5.Pod 的 3 种镜像拉取策略6.Pod 的 3 种容器重启策略 二、Pod进阶1.资源限制2.Pod 容器的 3 种探针(健康检查)3.探针的 3 种探测方式探针参…...

【小曾同学赠书活动】开始啦—〖测试设计思想〗
文章目录 ❤️ 赠书 —《测试设计思想》🌟 书籍介绍🌟 作者简介图书链接❤️ 活动介绍 — 赠送 3 本 ❤️ 赠书 —《测试设计思想》 首先提问 你知道测试设计思想有哪几类吗?你想奠定扎实的测试理论基础吗?你想改变关于你当前测试…...

【Docker晋升记】No.1--- Docker工具核心组件构成(镜像、容器、仓库)及性能属性
文章目录 前言🌟一、Docker工具🌟二、Docker 引擎🌏2.1.容器管理:🌏2.2.镜像管理:🌏2.3.资源管理:🌏2.4.网络管理:🌏2.5.存储管理:&am…...

ROBOGUIDE教程:FANUC机器人X型焊枪气动点焊焊接
目录 概述 机器人系统创建 X型点焊焊枪安装与配置 机器人组输出(GO)信号配置 气动点焊初始设置 点焊设备设置 点焊设备I/O信号设置 焊接控制器I/O信号设置 X型点焊焊枪运动控制配置 气动焊枪手动运行操作 气动点焊焊接指令介绍 机器人点焊焊接程序编写 机器人仿…...

二、 根据用户行为数据创建ALS模型并召回商品
二 根据用户行为数据创建ALS模型并召回商品 2.0 用户行为数据拆分 方便练习可以对数据做拆分处理 pandas的数据分批读取 chunk 厚厚的一块 相当大的数量或部分 import pandas as pd reader pd.read_csv(behavior_log.csv,chunksize100,iteratorTrue) count 0; for chunk in …...
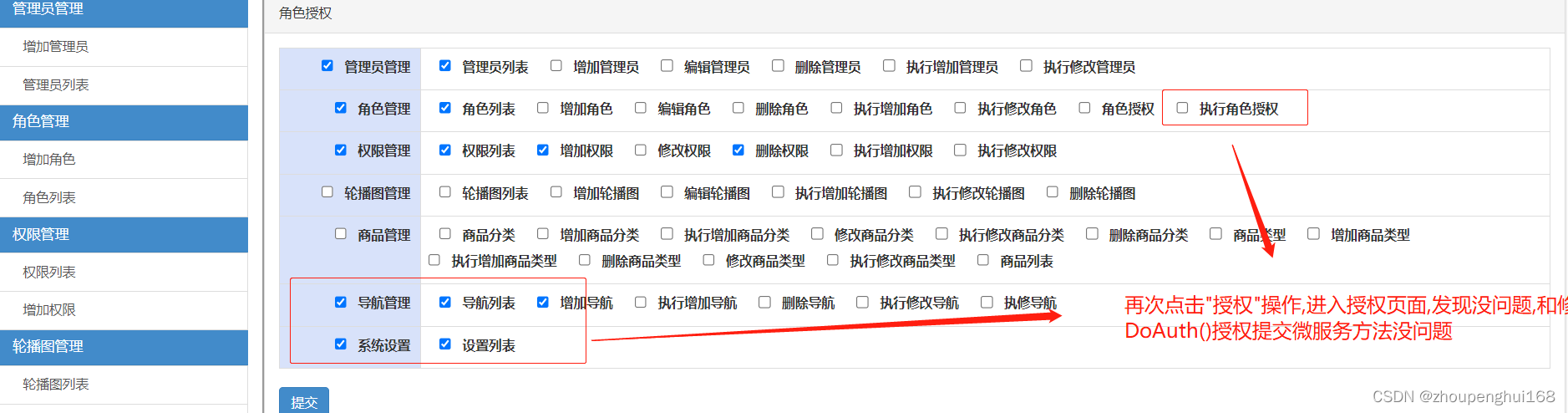
[golang gin框架] 45.Gin商城项目-微服务实战之后台Rbac微服务之角色权限关联
角色和权限的关联关系在前面文章中有讲解,见[golang gin框架] 14.Gin 商城项目-RBAC管理之角色和权限关联,角色授权,在这里通过微服务来实现角色对权限的授权操作,这里要实现的有两个功能,一个是进入授权,另一个是,授权提交操作,页面如下: 一.实现后台权限管理Rbac之角色权限关…...
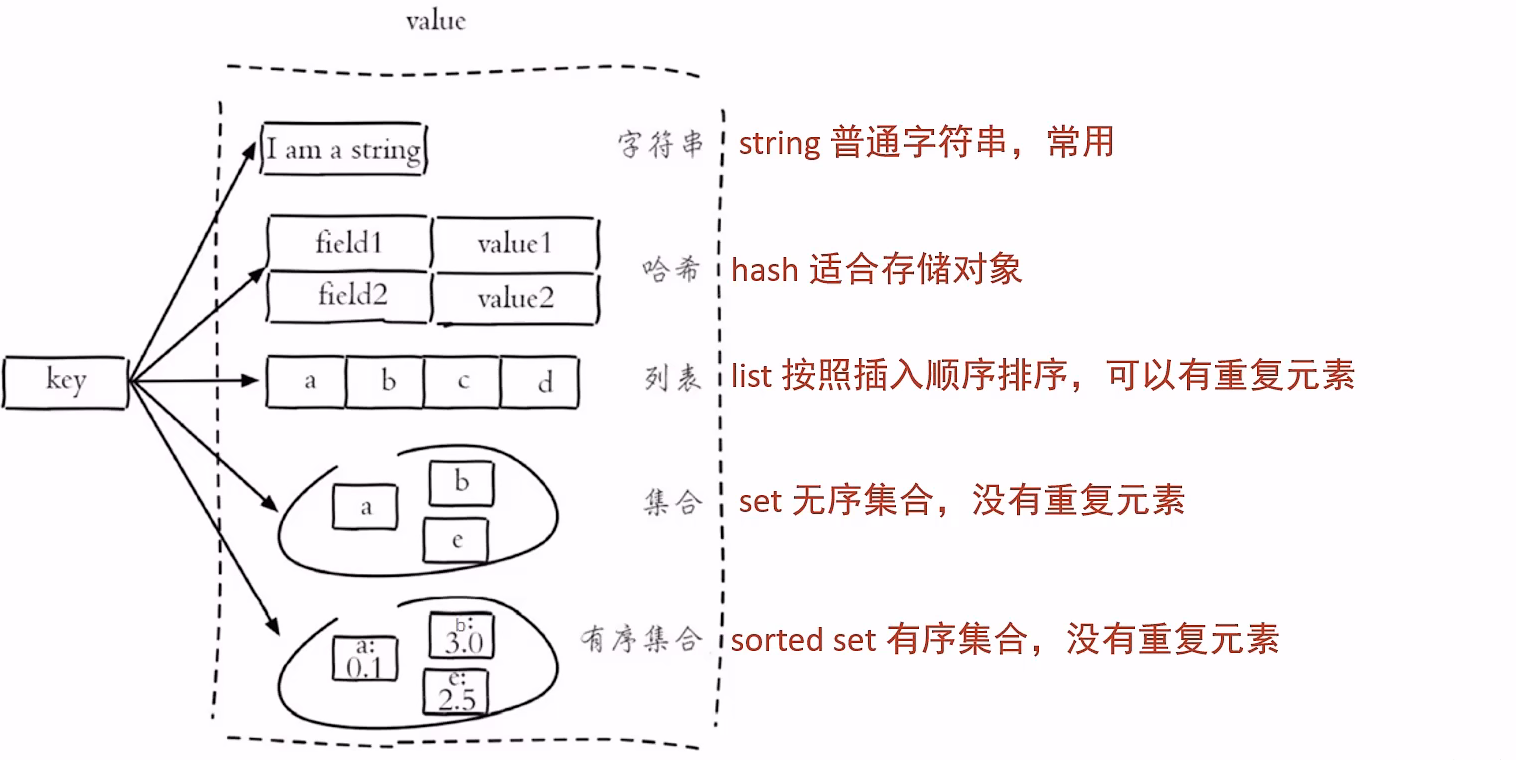
Redis中的数据类型
Redis中的数据类型 Redis存储的是key-value结构的数据,其中key是字符串类型,value有5种常用的数据类型: 字符串string哈希hash列表list集合set有序集合sorted set...
java spring cloud 企业工程管理系统源码+二次开发+定制化服务 em
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目显…...
Java程序猿搬砖笔记(十五)
文章目录 在Java中将类作为参数传递(泛型)IDEA快捷键:查看该方法调用了哪些方法、被哪些方法调用快捷键:ctrlalth IDEA快捷键:快速从controller跳转到serviceImplIDEA快捷键:实现接口的方法IDEA 快捷键:快速包裹代码ID…...

flask----内置信号的使用/django的信号/ flask-script/sqlalchemy介绍和快速使用/sqlalchemy介绍和快速使用
信号 内置信号的使用 # 第一步:写一个函数 def test(app, **kwargs):print(app)print(type(kwargs))# 请求地址是根路径,才记录日志,其它都不记录print(kwargs[context][request].path)if kwargs[context][request].path /:print(记录日志…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
