ARC126D Pure Straight
ARC126D Pure Straight
题目大意
给一个长度为nnn的整数序列A=(a1,a2,…,an)A=(a_1,a_2,\dots,a_n)A=(a1,a2,…,an),其中ai∈[1,k]a_i\in [1,k]ai∈[1,k]。
你可以做如下操作任意次:
- 交换相邻两个元素
求最小的操作次数,使得序列AAA满足下列条件:
- AAA包含(1,2,…,k)(1,2,\dots,k)(1,2,…,k)这个子串
2≤k≤16,k≤n≤2002\leq k\leq 16,k\leq n\leq 2002≤k≤16,k≤n≤200
题解
我们可以先将在111到kkk内的数移到一段,然后在这一段区间内排序。
令构成子串的元素的下标从小到大依次为c1,c2,…,cnc_1,c_2,\dots,c_nc1,c2,…,cn,中点位置为mid=⌊k2⌋mid=\lfloor\dfrac k2\rfloormid=⌊2k⌋,则显然让所有acia_{c_i}aci向acmida_{c_mid}acmid移动是最优的,总步数为
(∑i=1mid−1(cmid−mid+i)−ci)+(∑i=mid+1kci−(cmid+i−mid))(\sum\limits_{i=1}^{mid-1}(c_{mid}-mid+i)-c_i)+(\sum\limits_{i=mid+1}^kc_i-(c_{mid}+i-mid))(i=1∑mid−1(cmid−mid+i)−ci)+(i=mid+1∑kci−(cmid+i−mid))
我们发现这个式子中的许多地方可以抵消,最后式子可变为
(∑i=mid+1kci)−(∑i=1mid−1ci)−cmid×(n%2==0)+mid×(n%2==0)+(∑i=1mid−1i)−(∑i=mid+1ki)(\sum\limits_{i=mid+1}^kc_i)-(\sum\limits_{i=1}^{mid-1}c_i)-c_{mid}\times (n\%2==0)+mid\times(n\%2==0)+(\sum\limits_{i=1}^{mid-1}i)-(\sum\limits_{i=mid+1}^ki)(i=mid+1∑kci)−(i=1∑mid−1ci)−cmid×(n%2==0)+mid×(n%2==0)+(i=1∑mid−1i)−(i=mid+1∑ki)
后面mid×(n%2==0)+(∑i=1mid−1i)−(∑i=mid+1ki)mid\times(n\%2==0)+(\sum\limits_{i=1}^{mid-1}i)-(\sum\limits_{i=mid+1}^ki)mid×(n%2==0)+(i=1∑mid−1i)−(i=mid+1∑ki)是可以O(1)O(1)O(1)求出的,我们来看看如何求前面的部分。
可以用状压DP,设fi,sf_{i,s}fi,s表示枚举到AAA的第iii位时状态为sss,sss的二进制位111表示已取过这个数字,000表示没取过这个数字。我们需要预处理数组hvshv_shvs,表示sss的二进制位中有多少个111。
状态转移式如下
fi,s∣(1<<ai−1)={fs−i+ps,aihvs+1<midfs−i×(k%2==0)+ps,aihvs+1=midfs+i+ps,aihvs+1>midf_{i,s|(1<<a_i-1)}= \left\{\begin{matrix} f_s-i+p_{s,a_i} \qquad\qquad\qquad\qquad \ \ hv_s+1<mid \\ f_s-i\times(k\%2==0)+p_{s,a_i} \qquad hv_s+1=mid\\ f_s+i+p_{s,a_i} \qquad\qquad\qquad\qquad \ \ hv_s+1>mid \end{matrix}\right.fi,s∣(1<<ai−1)=⎩⎨⎧fs−i+ps,ai hvs+1<midfs−i×(k%2==0)+ps,aihvs+1=midfs+i+ps,ai hvs+1>mid
其中fi,s∣(1<<ai−1)f_{i,s|(1<<a_i-1)}fi,s∣(1<<ai−1)与后面的部分取max\maxmax。
下面来解释一下ppp是什么。因为在将111到kkk内的数移到一段后,内部还要调整。根据冒泡排序的原理,若要用最少的操作次数排好序,每个数对操作次数的贡献为在它之前比他大的数的个数。ps,ip_{s,i}ps,i表示在sss中二进制位数大于iii且该位为111的数量,在转移式中表示加入这个元素的贡献。
求出fff后,加上mid×(n%2==0)+(∑i=1mid−1i)−(∑i=mid+1ki)mid\times(n\%2==0)+(\sum\limits_{i=1}^{mid-1}i)-(\sum\limits_{i=mid+1}^ki)mid×(n%2==0)+(i=1∑mid−1i)−(i=mid+1∑ki)即为答案。
时间复杂度为O(n⋅2k)O(n\cdot2^k)O(n⋅2k)。
code
#include<bits/stdc++.h>
using namespace std;
int n,k,mid,ans,a[205],v[20],hv[1<<16],p[1<<16][20],f[1<<16];
void pd(int now){f[now]=1000000000;int s=0;for(int i=k;i>=1;i--){p[now][i]=s;s+=v[i];}hv[now]=s;
}
void dfs(int t,int now){if(t<k) dfs(t+1,now);else pd(now);now+=(1<<t-1);v[t]=1;if(t<k) dfs(t+1,now);else pd(now);v[t]=0;
}
int main()
{scanf("%d%d",&n,&k);mid=(k+1)/2;for(int i=1;i<=n;i++){scanf("%d",&a[i]);}dfs(1,0);f[0]=0;for(int i=1;i<=n;i++){for(int s=(1<<k)-1;s>=0;s--){if(s&(1<<a[i]-1)) continue;int t=s|(1<<a[i]-1);if(hv[s]+1<mid) f[s|t]=min(f[s|t],f[s]-i+p[s][a[i]]);else if(hv[s]+1==mid) f[s|t]=min(f[s|t],f[s]-i*(k%2==0)+p[s][a[i]]);else f[s|t]=min(f[s|t],f[s]+i+p[s][a[i]]);}}ans=f[(1<<k)-1];if(k%2==0) ans+=mid;ans=ans+(mid)*(mid-1)/2-(k-mid)*(k+mid+1)/2;printf("%d",ans);return 0;
}
相关文章:

ARC126D Pure Straight
ARC126D Pure Straight 题目大意 给一个长度为nnn的整数序列A(a1,a2,…,an)A(a_1,a_2,\dots,a_n)A(a1,a2,…,an),其中ai∈[1,k]a_i\in [1,k]ai∈[1,k]。 你可以做如下操作任意次: 交换相邻两个元素 求最小的操作次数,使得序列AA…...
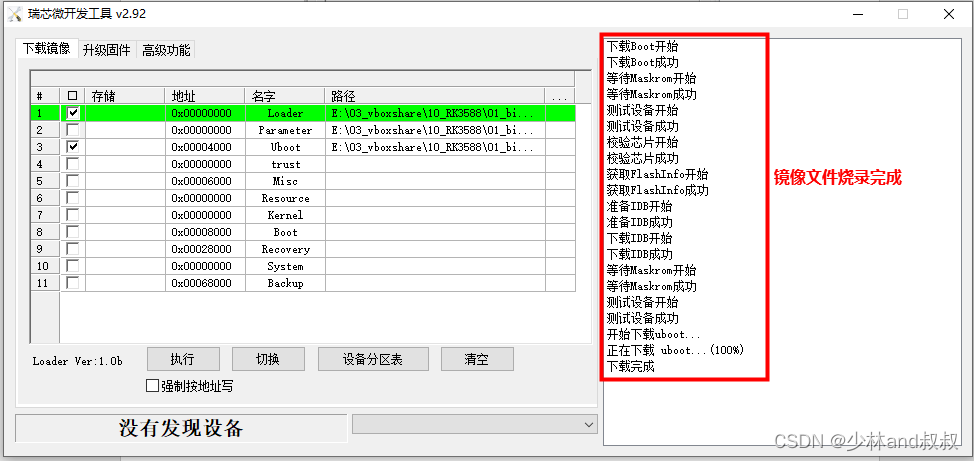
基于RK3588的嵌入式linux系统开发(四)——uboot镜像下载(基于RKDevTool工具)
官方提供的SDK中包含RKDevTool工具(RKDevTool_Release_v2.92)和相应的驱动(DriverAssitant_v5.1.1)。本节主要介绍在windows操作系统环境下利用RKDevTool下载以上生成的uboot镜像和bootloader镜像。注意:本节使用的板卡…...
设计模式之策略模式与责任链模式详解和应用
目录1.策略模式1.1 目标1.2.内容定位1.3.定义1.4.应用场景1.5.促销优惠业务场景1.6 用策略模式实现选择支付方式的业务场景1.7 策略模式在框架源码中的体现1.8 策略模式的优缺点2 责任链模式2.1 责任链楼式的应用场景2.2 利用责任链模式进行数据校验拦截2.3 责任链模式和建造者…...

广度优先搜索(BFS)-蓝桥杯
一、BFS搜索的原理BFS搜索的原理:“逐层扩散”,从起点出发,按层次从近到远,逐层先后搜索。编码:用队列实现。应用:BFS一般用于求最短路径问题,BFS的特点是逐层搜索,先搜到的层离起点…...
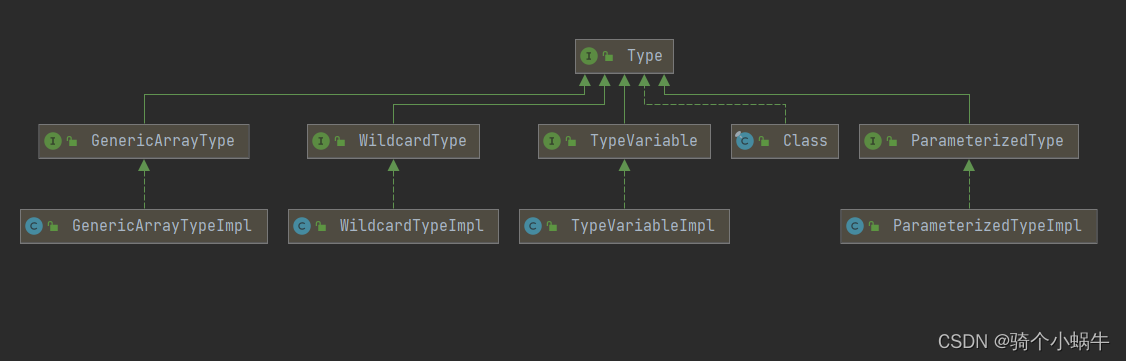
Java Type类
文章目录Type简介Type分类1. 原始类型(Class)2. 参数化类型(ParameterizedType)3. 类型变量(TypeVariable)4. 通配符类型(WildcardType)5. 泛型数组类型(GenericArrayType)Type简介 Type是Java编程语言中所有类型的公共高级接口。它们包括原始类型、参数化类型、数组类型、类型…...
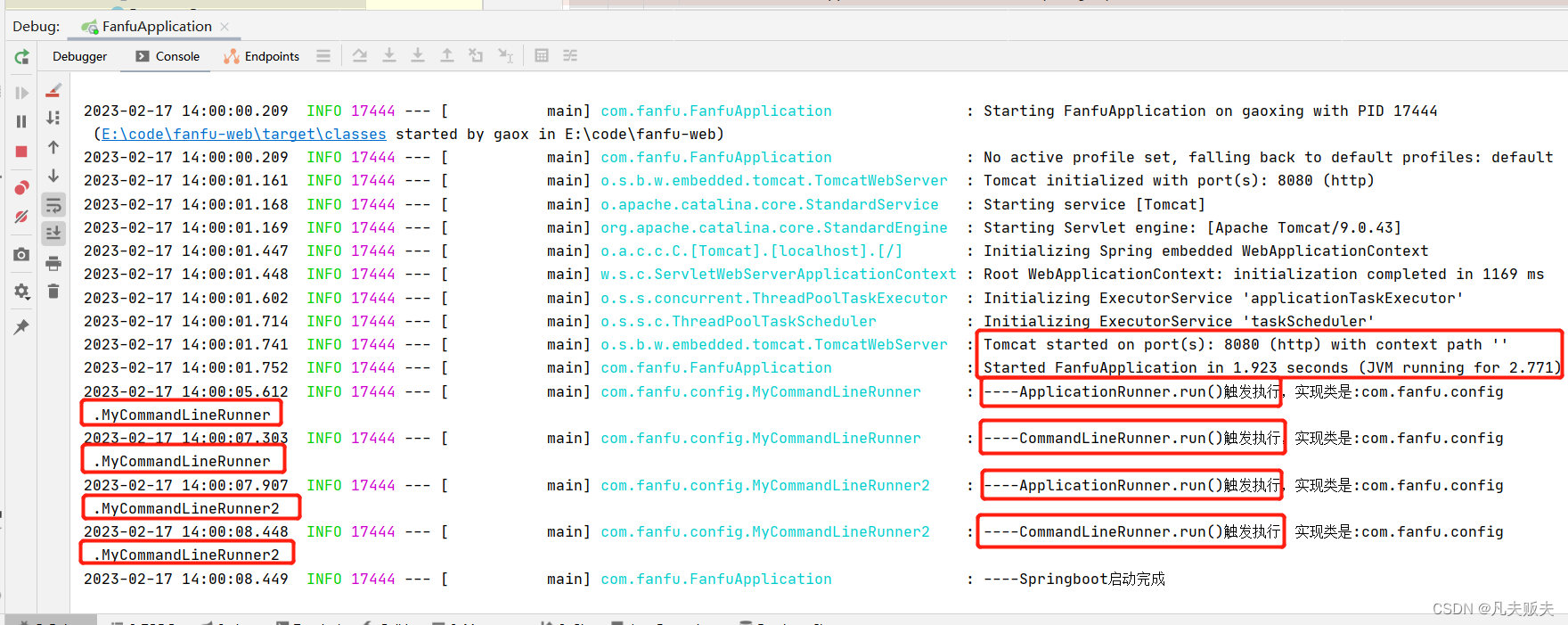
Springboot扩展点之CommandLineRunner和ApplicationRunner
Springboot扩展点系列:Springboot扩展点之ApplicationContextInitializerSpringboot扩展点之BeanFactoryPostProcessorSpringboot扩展点之BeanDefinitionRegistryPostProcessorSpringboot扩展点之BeanPostProcessorSpringboot扩展点之InstantiationAwareBeanPostPro…...

ngixn 常用配置之文件类型与自定义 log
大家好,我是 17 。 总结了一些 nginx 的常用配置。从入口文件开始,今天讲一下文件类型和自定义log 为了讲述方便,环境为 CentOS 7, nginx 版本 1.21。 配置文件入口 /etc/nginx/nginx.conf这是入口文件,这个文件里…...

【100个 Unity实用技能】 | Unity 通过自定义菜单将资源导出
Unity 小科普 老规矩,先介绍一下 Unity 的科普小知识: Unity是 实时3D互动内容创作和运营平台 。包括游戏开发、美术、建筑、汽车设计、影视在内的所有创作者,借助 Unity 将创意变成现实。Unity 平台提供一整套完善的软件解决方案ÿ…...
0.3调试opencv源码的两种方式
调试opencv源码的两种方式 上两篇我们分别讲了如何配置opencv环境,以及如何编译opencv源码方便我们阅读。但我们还是无法调试我们的代码,无法以我们的程序作为入口来一步一步单点调试看opencv是如何执行的。 【opencv源码解析0.1】VS如何优雅的配置ope…...

Redis的常见操作和Session的持久化
安装Redis使用yum命令,直接将redis安装到linux服务器:yum -y install redis启动redis使用以下命令,以后台运行方式启动redis:redis -server /etc/redis.conf &操作redis使用以下命令启动redis客户端:redis-cli设置…...
)
TypeScript笔记(二)
背景 上一篇文章我们介绍了TypeScript的一些特性,主要是其与JavaScript的比较,接下来我们将会开始学习Type的语法,这篇文章将会介绍TypeScript的数据类型。 原始数据类型 TypeScript是JavaScript的超集,TypeScript的数据类型就…...
【MyBatis】源码学习 03 - 类型处理器 TypeHandler
文章目录前言参考目录学习笔记1、type 包中类的归类总结2、类型处理器2.1、TypeReference 类3、类型注册表3.1、TypeHandlerRegistry#getTypeHandler前言 本文内容对应的是书本第 8 章的内容,主要是关于类型处理器 TypeHandler 的学习。 这一章节的学习有些地方理…...

建造《流浪地球2》中要毁灭人类的超级量子计算机MOSS的核心量子技术是什么?
1.《流浪地球2》中的量子计算机 2023年中国最火的电影非《流浪地球2》莫属,在《流浪地球2》中有一个人工智能机器人MOSS ,它的前身是“550W”超级量子计算机,“MOSS”是它给自己起的名字(“550W”倒转180度就是“MOSS”ÿ…...
)
数据结构~七大排序算法(Java实现)
目录 插入排序 直接插入排序 希尔排序 选择排序 直接选择排序 堆排序 交换排序 冒泡排序 快速排序 递归实现 优化版本 归并排序 插入排序 直接插入排序 public class MySort {public static void insertSort(int[] array) {for (int i 1; i < array.length;…...
python练习
项目场景一: 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 问题描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶…...

RPC-thrift实践
参考:https://www.cnblogs.com/52fhy/p/11146047.html 参考:https://juejin.cn/post/7138032523648598030 实践 安装thrift brew install thriftthrift -version 编写thrift文件 新建文件夹thrift新建文件 结构体文件 Struct.thrift 服务文件 Service.…...
Maven:工程的拆分与聚合
Maven 拆分与聚合创建父工程创建子模块pom.xml配置示例拆分与聚合 在 Maven 中, 拆分是将一个完整的项目分成一个个独立的小模块,聚合是将各个模块进一步组合,形成一个完整的项目。接下来简单示例拆分与聚合的过程。 创建父工程 父工程,一个pom工程,目录结构简单,只需有…...
使用uniapp创建小程序和H5界面
uniapp的介绍可以看官网,接下来我们使用uniapp创建小程序和H5界面,其他小程序也是可以的,只演示创建这2个,其实都是一套代码,只是生成的方式不一样而已。 uni-app官网 1.打开HBuilder X 选择如图所示,下…...

密度峰值聚类算法(DPC)
密度峰值聚类算法目录DPC算法1.1 DPC算法的两个假设1.2 DPC算法的两个重要概念1.3 DPC算法的执行步骤1.4 DPC算法的优缺点matlab代码密度计算函数计算delta寻找聚类中心点聚类算法目录 DPC算法 1.1 DPC算法的两个假设 1)类簇中心被类簇中其他密度较低的数据点包围…...
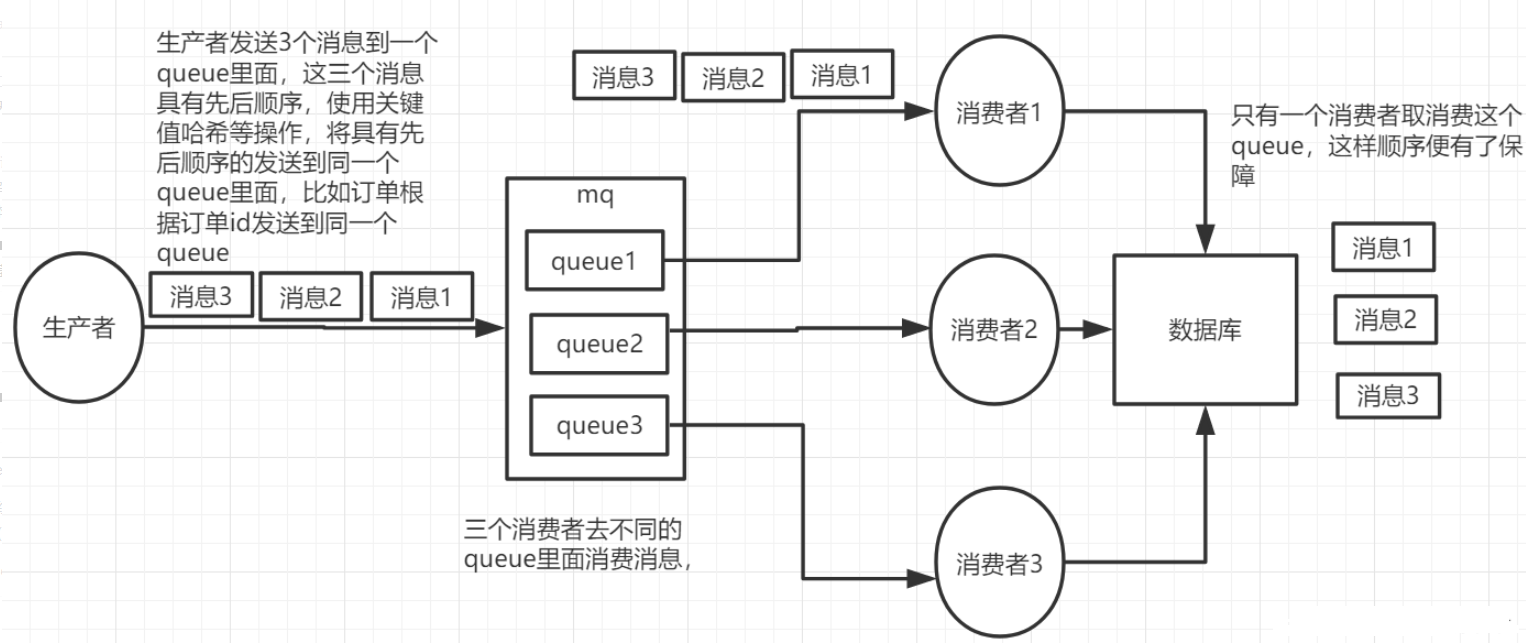
RabbitMQ相关问题
文章目录避免重复消费(保证消息幂等性)消息积压上线更多的消费者,进行正常消费惰性队列消息缓存延时队列RabbitMQ如何保证消息的有序性?RabbitMQ消息的可靠性、延时队列如何实现数据库与缓存数据一致?开启消费者多线程消费避免重复消费(保证消…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
