python中常见的矩阵变换总结
利用python做数据处理和分析过程中,如在开展机器学习的数据预处理、数据格式转换等等,不可避免的会涉及到各种矩阵变换,其中使用最多的就是numpy下的矩阵变换,以下是日常用到的一些矩阵变换总结,主要有矩阵中数据类型的整体转换、矩阵维度增减、多矩阵拼接、矩阵切片获取和多矩阵迭代等等,当然,pandas也有相应的矩阵变换操作,相对更复杂,后续会逐步发出来,供参考。
1.转换元素类型和增加维度
import numpy as np
data_pre=np.random.randint(2,10,size=[5,3]) #生成一个5*3的二维整形矩阵,数据范围在2~10之间
data_pre = np.array(data_pre, dtype=np.float32) #数据转换为float
target=np.random.random(10) #随机生成一个一维矩阵,10个数
target = np.array(target, dtype=np.float32).reshape(-1, 1) #数据转换为多行1列数据,相当于增加维度,float型,可以不用的。
data_pre= np.arange(0.0, 5.0, 0.1)[:, np.newaxis] #np.arange会生成一个一维矩阵,希望data_pre是一个二维矩阵,用np.newaxis相当于给数据增加一个维度
target=np.random.random(10) #随机生成一个一维矩阵,10个数
target=target.reshape(-1, 1) #实现行转换为列,转换前y_raw为100个数的一维矩阵,转换后y_raw为100*1的二维矩阵2.拉平或降低维度
rng = np.random.RandomState(42) #获得随机数生成器,使得每次得到的随机数系列相同
X = np.sort(5 * rng.rand(100, 1), axis=0) #获的100个0到5的随机数给X,X.shape=(100,1),二维
y = np.sin(X).ravel() #矩阵多维度拉成一维矩阵,ravel() 返回的是视图,影响原始矩阵y,flatten() 返回的是拷贝。y.shape=(100,)
import cv2
img_data = cv2.imread('data/lena.jpg', cv2.IMREAD_COLOR) #利用opencv读取图片
img_data = img_data.reshape((-1, 3)) #将三维转换为二维,相当于高度和宽度相乘合并,最后一维不变(3列),转换前img_data:225*225*3,转换后50625*3
#整体维度不变,实现第一个维度行数调整,相当于根据labels找到centers[labels]生成新的new_colors数据,按照labels行数增加,如centers:16*3,labels:50625*3,转换后的new_colors为50625*3
# new_colors = centers[labels].reshape((-1, 3))3.拼接矩阵
X_pos=np.random.randn(5,3) #随机生成一个10*3的二维矩阵
X_neg=np.random.randn(5,3) #随机生成一个10*3的二维矩阵
# 行拼接
#方式1:二维矩阵,列数不变,行数顺序追加,相当于行顺序拼接,两个矩阵的列数必须相同
X = np.concatenate((X_pos, X_neg))
#方式2:二维矩阵,列数不变,行数顺序追加,相当于行顺序拼接,两个矩阵的列数必须相同
X2=np.r_[X_pos,X_neg]
# 列拼接
#二维矩阵,行数不变,列数顺序追加,相当于列顺序拼接,两个矩阵的行数必须相同
X1=np.c_[X_pos,X_neg]
y_pos=np.random.random(3) #随机生成一个一维矩阵,3个数
y_neg=np.random.random(5) #随机生成一个一维矩阵,5个数
#一维矩阵,行数不变,列数顺序追加,相当于列顺序拼接
y = np.concatenate((y_pos, y_neg))4.获取矩阵片段
int_list=np.random.randn(10,5) #随机生成一个10*5的二维矩阵
#list获取切片
#int_list[start:stop:step],参数分别为开始,结束和步长
print(int_list)
#对于一维矩阵,获取第1维度的第0,2,4...,步长为2的数据
#对于二维矩阵,获取第2维度的第0~10列,并指定获取第一维度的步长为2,获取的行数=stop/step,如下示例时5行数据
print(int_list[0:10:2])
print(int_list[0:5,:4]) #获取第1维度的第0~5行,第2维度的前4列数据
#对于三维矩阵
arr_float_3d = np.ones((3, 5, 4))
print(arr_float_3d)
#多维list获取第一通道数据
x=arr_float_3d[0, :, :]
#多维list获取第一通道,0~3行数据,第3列到结束的数据
x=arr_float_3d[0, :3, 3:]5.zip内建函数
zip(*iterables)是内建函数
传入参数:元组、列表、字典等迭代器。
返回参数:一个元组迭代器,将可迭代的对象作为参数,将对象中对应的元素打包成一个个元组,然后返回由这些元组组成的列表。主要用于遍历元组。
如果各个迭代器的元素个数不一致,则返回列表长度与最短的对象相同,利用 * 号操作符,可以将元组解压为列表。
X1=np.random.random(5) #随机生成一个一维矩阵,5个数
Y1=np.random.randn(5).astype(np.int32) #随机生成一个一维矩阵,5个数,转换为整数
Z1=np.array([True, False, True, True, False]) #列表,bool值
zz=zip(X1,Y1,Z1)
result = [(a,b,c) for a,b,c in zip(X1,Y1,Z1)]
print(result)
x,y,z=zip(*zz) #元组转换为列表
print(list(x))
zz=zip() #没有参数时,返回的是空列表相关文章:

python中常见的矩阵变换总结
利用python做数据处理和分析过程中,如在开展机器学习的数据预处理、数据格式转换等等,不可避免的会涉及到各种矩阵变换,其中使用最多的就是numpy下的矩阵变换,以下是日常用到的一些矩阵变换总结,主要有矩阵中数据类型的…...
LightningChart JS 2023Crack,CPU高效实时更新
LightningChart JS 2023Crack,CPU高效实时更新 添加了新的极地热图图表类型-添加了新系列类型,允许您在极地坐标系中可视化热图。极地热图的一些关键特征是: 处理多达400万个数据点。 快速加载速度和CPU高效实时更新。 100ms以完全显示由所有数据填充的热…...
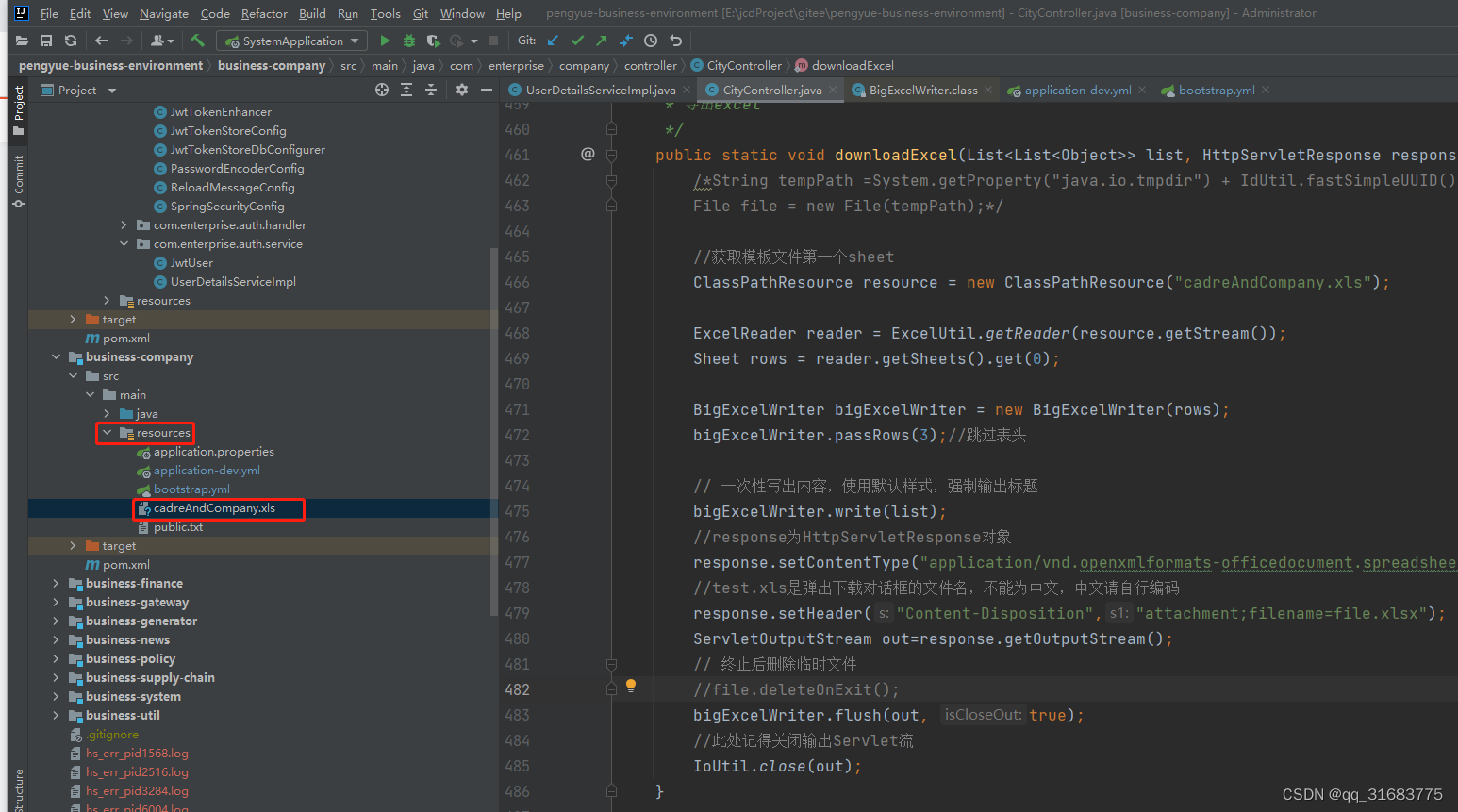
hutool 导出复杂表头excel
假如已这样的表头导出数据 1.把包含表头的excel添加到项目资源目录 2.编写代码读取表头所在sheet,并且加入需导出的数据 /*** 导出excel*/public static void downloadExcel(List<List<Object>> list, HttpServletResponse response) throws IOException {/*Strin…...
git和github学习
一、什么是git和github? 二、学会使用github desktop应用程序 初始使用: 一开始我们是新账户,里面是没有仓库的,需要手动创建一个仓库。此时,这个仓库是创建在本地仓库里面,需要用到push命令(就是那个pub…...

竞赛项目 车位识别车道线检测 - python opencv
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习 机器视觉 车位识别车道线检测 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🥇学长这里给一个题目综合评分(每项满分5分) …...

中文版开源Llama 2同时有了语言、多模态大模型,完全可商用
可以说,AI 初创公司 LinkSoul.Al 的这些开源项目让海外开源大模型在国内的普及和推广速度与国际几乎保持了一致。 7 月 19 日,Meta 终于发布了免费可商用版本 Llama 2,让开源大模型领域的格局发生了巨大变化。 Llama 2 模型系列包含 70 亿、…...
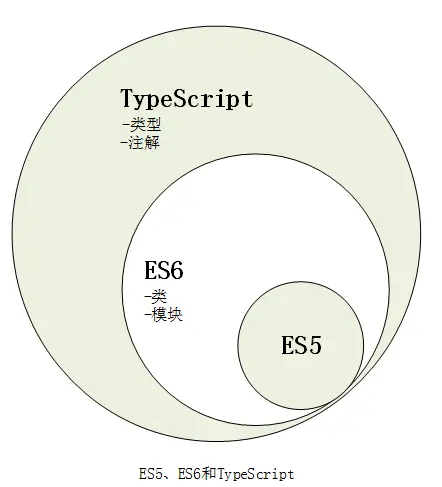
JavaScript、TypeScript、ES5、ES6之间的联系和区别
ECMAScript: 一个由 ECMA International 进行标准化,TC39 委员会进行监督的语言。通常用于指代标准本身。JavaScript: ECMAScript 标准的各种实现的最常用称呼。这个术语并不局限于某个特定版本的 ECMAScript 规范,并且可能被用于…...
RCNA——单臂路由
一,实验背景 之前的VLAN实现的很多都是相同部门互相访问,不同部门无法访问。不过这次整来了一个路由器,领导说大部分的部门虽说有保密信息需要互相隔离,但是这些部门和其它部门也应该互相连通以方便工作交流。因此要配置新的环境&…...

leetcode做题笔记69
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。 注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。 思路一ÿ…...
!)
CentOS根分区扩容实战(非LVM)!
在虚拟化平台(如KVM,ESXI)中,将虚拟机的磁盘大小扩展到所需的大小。这将增加虚拟机的磁盘空间。 在虚拟机中,使用以下命令查看可用的磁盘和分区信息: sudo fdisk -l确定要扩展的根分区的设备名称(如 /dev/…...
uniapp 微信小程序 分包
1、manifest.json内添加如图所示: "optimization" : {"subPackages" : true },2、在与pages同级上创建各个分包的文件夹 把需要分包的文件对应移入分包文件夹内 3、page.json内修改分包文件的路径 比如: {"path" : &qu…...

Redis_安装、启动以及基本命令
2.Redis安装 2.1前置处理环境 VMware安装安装centOS的linux操作系统xshellxftp 2.2 配置虚拟机网络 按ctrlaltf2 切换到命令行 cd (/)目录 修改/etc/sysconfig/network-scripts/ifcfg-ens3 vi 命令 按insert表示插入 按ctrlesc退出修改状态 :wq 写入并退出 此文件必须保持一…...

IPv4编址及子网划分
IPv4编址及子网划分 一、IPv4地址概述1.1、IPv4报文结构1.2、IPv4地址分类1.2.1、A类1.2.2、B类1.2.3、C类1.2.4、D类1.2.5、E类 1.3、私有IP地址1.4、特殊地址 二、子网划分2.1、子网掩码2.2、VLSM 可变长的子网掩码2.3、子网划分2.4、子网划分示例2.4.1、子网划分案例 —— A…...
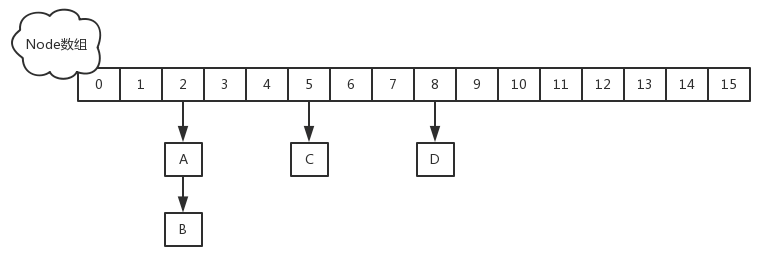
HashMap 二十一问
1:HashMap 的数据结构? A:哈希表结构(链表散列:数组链表)实现,结合数组和链表的优点。当链表长度超过 8 时,链表转换为红黑树。transient Node<K,V>[] table; 2:…...
什么是Selenium?使用Selenium进行自动化测试
什么是 Selenium? Selenium 是一种开源工具,用于在 Web 浏览器上执行自动化测试(使用任何 Web 浏览器进行 Web 应用程序测试)。 等等,先别激动,让我再次重申一下,Selenium 仅可以测试We…...

解决“先commit再pull”造成的git冲突
一、问题场景 在分支上修改了代码然后commit(没有push),此时再git pull,拉下了别人的修改,但是报错无法merge 二、解决步骤 1.在idea下方工具栏选择git -> log,可以看到版本变化链表,右键…...
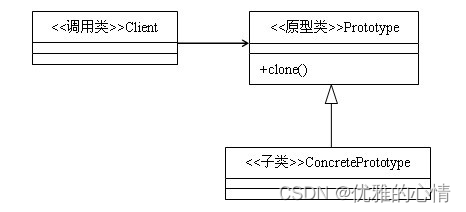
JAVA设计模式----原型设计模式
文章目录 一、简介二、实现方式三、原型模式的注意事项浅拷贝与深拷贝浅拷贝深拷贝一、简介 定义:用原型实例指定创建对象的种类,并通过拷贝这些原型创建新的对象。 类型:创建类模式 类图: 原型模式主要用于对象的复制,它的核心是就是类图中的原型类Prototype。Protot…...

树·c++
树(Tree) 是一种非线性的数据结构,它由若干个 节点(Node) 组成,并通过 边(Edge) 相互连接。树的结构类似于现实中的树,其中 根节点(Root Node) 位…...
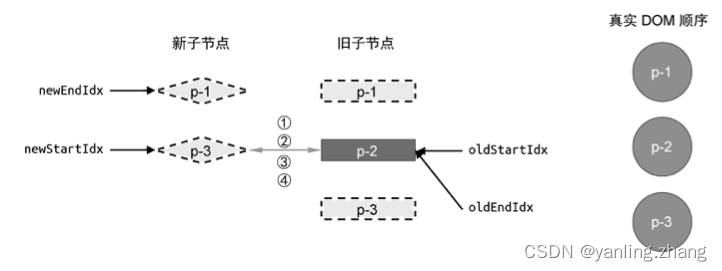
vuejs 设计与实现 - 双端diff算法
我们介绍了简单 Diff 算法的实现原理。简单 Diff 算法利用虚拟节点的 key 属性,尽可能地复用 DOM元素,并通过移动 DOM的方式来完成更新,从而减少不断地创建和销毁 DOM 元素带来的性能开销。但是,简单 Diff 算法仍然存在很多缺陷&a…...

RISC-V在快速发展的处理器生态系统中找到立足点
原文:RISC-V Finds Its Foothold in a Rapidly Evolving Processor Ecosystem 作者:Agam Shah 转载自:https://thenewstack.io/risc-v-finds-its-foothold-in-a-rapidly-evolving-processor-ecosystem/ 以下是正文 But the open source pr…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
