基于R做宏基因组的进化树ClusterTree分析
写在前面
同上一篇的PCoA分析,这个也是基于公司结果基础上的再次分析,重新挑选样本,在公司结果提供的csv结果表上进行删减,本地重新分析作图
步骤
表格预处理
- 在公司给的ClusterTree的原始表格数据里选取要保留的样本,同样保存为逗号分隔的csv文件
代码演示
无色版
install.packages('vegan')
install.packages('dendextend')
install.packages('circlize')data <- read.table('F:\\Analysis\\RA_Sanhe cow\\Microgenome\\Cluster_Tree\\table.g10.cluster.csv', header=T, sep = ',', check.names=FALSE)
rownames(data)=data[,1]
data=data[,-1]
library(vegan)
data=decostand(data, MARGIN=2, "total")
otu=t(data)
otu_dist=vegdist(otu, method="bray", diag=TRUE, upper=TRUE, p=2)
#进行聚类分析并作图
hclust=hclust(otu_dist, method="average")
plot(hclust)library(dendextend)
library(circlize)
tree=as.dendrogram(hclust)
par(mfrow=c(2,2), mar=c(3,3,1,5), cex=0.7)
plot(tree, horiz=TRUE, main="UPGMA Tree")
#隐藏平均距离小于0.5的对象(类群)
plot(cut(tree, h=0.5)$upper, horiz=TRUE, main="Samples with distance higher than 0.5")
#在上一步基础上筛选第二个分类簇
plot(cut(tree, h=0.5)$upper[[2]], horiz=TRUE, main="Second branch samples with distance higher than 0.5")
circlize_dendrogram(tree)
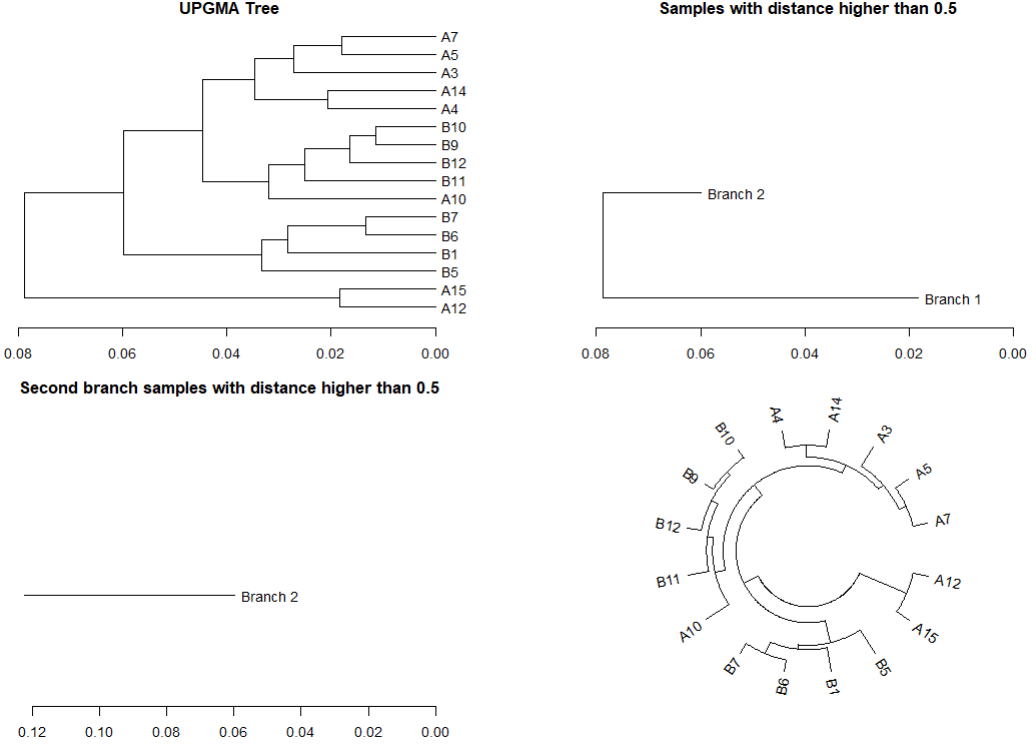
上色版
##完整代码
data <- read.table('F:\\Analysis\\RA_Sanhe cow\\Microgenome\\Cluster_Tree\\Demo_ClusterTree.csv', header=T, sep = ',', check.names=FALSE)
rownames(data)=data[,1]
data=data[,-1]
library(vegan)
data=decostand(data, MARGIN=2, "total")
otu=t(data)
otu_dist=vegdist(otu, method="bray", diag=TRUE, upper=TRUE, p=2)
#进行聚类分析并作图
hclust=hclust(otu_dist, method="average")
library(dendextend)
library(RColorBrewer)
hcd=as.dendrogram(hclust)
labelColors=brewer.pal(n=4, name="Set1")
#聚类分组,预设聚类簇数目为4
clusMember=cutree(hcd, 4)
#自定义函数,根据聚类结果进行着色,4 种颜色
colLab=function(n) {if (is.leaf(n)) {a=attributes(n)labCol=labelColors[clusMember[which(names(clusMember)==a$label)]]attr(n, "nodePar")=c(a$nodePar, lab.col=labCol)}n
}
clusDendro=dendrapply(hcd, colLab)
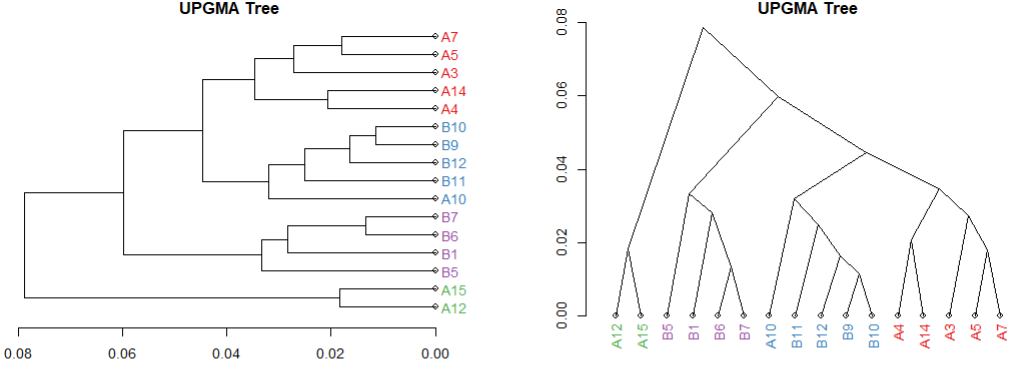
plot(clusDendro, main ="UPGMA Tree", type="rectangle", horiz=TRUE)
plot(clusDendro, main ="UPGMA Tree", type="triangle")
相关文章:

基于R做宏基因组的进化树ClusterTree分析
写在前面 同上一篇的PCoA分析,这个也是基于公司结果基础上的再次分析,重新挑选样本,在公司结果提供的csv结果表上进行删减,本地重新分析作图 步骤 表格预处理 在公司给的ClusterTree的原始表格数据里选取要保留的样本…...
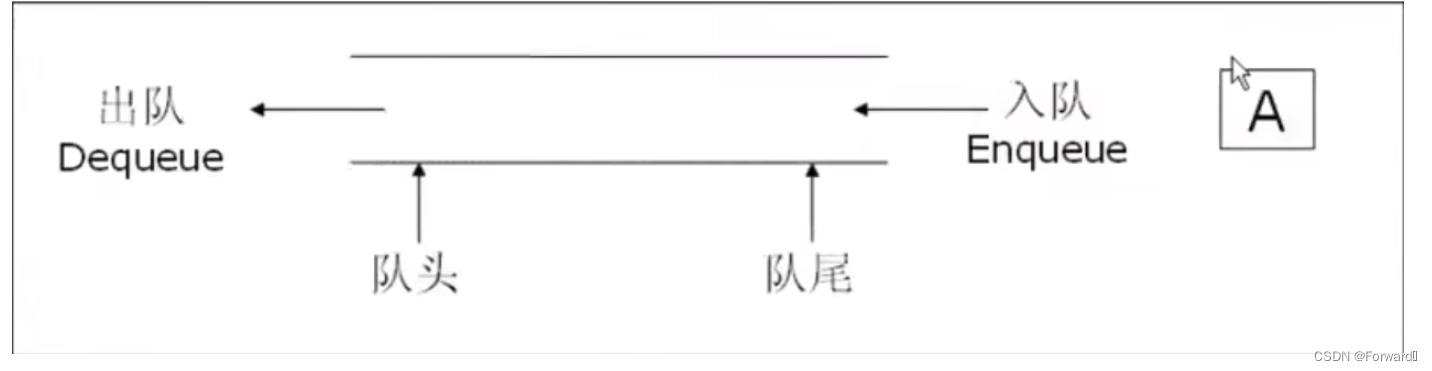
栈和队列修炼指南(基本操作+OJ练习)
栈和队列修炼指南 1. 栈 1. 1 概念及结构 栈:是一种特殊的线性表,其只允许在固定的一端进行插入和删除元素的操作。进行数据插入和删除操作的一端称为栈顶,另一端为栈底。 栈中的数据元素遵守后进先出原则(LIFO)原则 压栈:栈的…...

伪类和伪元素有何区别?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 伪类(Pseudo-class)⭐ 伪元素(Pseudo-element)⭐ 区别总结⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前…...

自动测试框架airtest应用一:将XX读书书籍保存为PDF
一、Airtest的简介 Airtest是网易出品的一款基于图像识别和poco控件识别的一款UI自动化测试工具。Airtest的框架是网易团队自己开发的一个图像识别框架,这个框架的祖宗就是一种新颖的图形脚本语言Sikuli。Sikuli这个框架的原理是这样的,计算机用户不需要…...

ValueError:The following settings are not supported :{‘username‘: ‘neo4j“}
py2neo版本不同所导致的问题,下面我通过一段代码说明该问题。 import py2neoif py2neo.__version__ 4.3.0:graph Graph(http://localhost:7474, username config.neo4j_username, password config.neo4j_password) elif py2neo.__version__ 2021.2.3:graph G…...
360安全卫士右下角广告弹窗太多怎么彻底关闭?
360安全卫士右下角广告弹窗太多怎么彻底关闭? 1、卸载360安全卫士,选择继续卸载,并点击下一步; 2、选择广告弹窗太多,并点击下一步; 3、然后被告知升级极速版永久去广告,可以点击一键去广告。 …...
链表有无环以及确定入环口详解
142.环形链表 II 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测…...

chrome插件开发实例08- 使用Vue.js开发chrome插件
目录 背景 演示 功能介绍 插件下载 注意写法: 背景 将 下面的两个插件 改写成vue.js , elementui 实现chrome插件开发实例0...

PCL 计算外接圆的半径
目录 一、算法原理1、计算公式2、主要函数3、源码解析二、代码实现三、结果展示四、参考链接本文由CSDN点云侠原创,原文链接。爬虫自重。 一、算法原理 1、计算公式...
)
Matlab实现神经网络SOM算法(附上完整仿真源码)
神经网络SOM算法是一种基于自组织的无监督学习算法,其全称为Self-Organizing Map,可以用来对数据进行聚类和可视化。本文将介绍如何使用Matlab实现神经网络SOM算法。 文章目录 一、准备工作二、数据准备三、SOM算法实现四、聚类结果分析五、总结六、完整…...
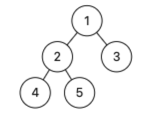
【遍历】非递归法 二叉树的前中后序遍历
文章目录 非递归法前序遍历后序遍历中序遍历 递归法DFS 非递归法 通过栈Stack来模拟递归。 前序遍历 LeetCode 144 前序遍历:1 2 3 定义:存放答案的List、栈Stack 将root入栈出栈:node,为null则舍弃将node放入list将node.r…...

Python将tiff转换成png
文章目录 问题描述解决方案压缩并转换参考文献 问题描述 base64 的 image/tiff 无法在页面直接展示,将其转换为 image/png 解决方案 from io import BytesIOfrom PIL import Imagewith Image.open(a.tiff) as image:bytesIO BytesIO()image.save(bytesIO, format…...

【大数据】-- 部署 Flink kubernetes operator
目录 1.说明 1.1 版本 1.2 kubernetes 环境 1.3 参考 2.安装步骤 2.1 安装本地 kubernetes 环境...
方式)
能够完成两个数的算术运算的单地址指令,地址码指明一个操作数,另一个操作数来自( )方式
【计算机组成原理错题】能够完成两个数的算术运算的单地址指令,地址码指明一个操作数,另一个操作数来自( )方式。 A.立即寻址 B.隐含寻址 C.间接寻址 D.基址寻址 正确答案:B 因为另一个操作数来自于累加器ACC,而这种方式属于隐含寻址。 在指令…...
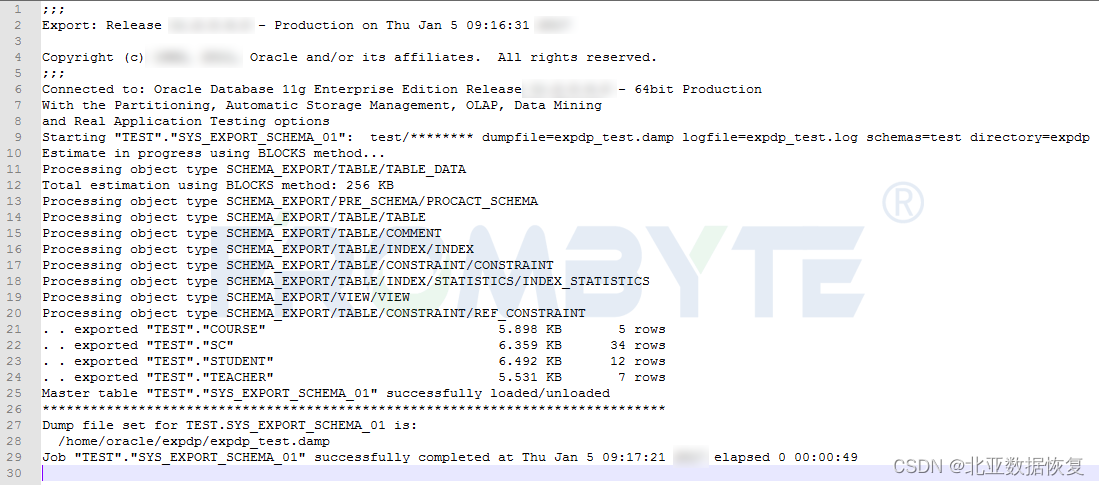
数据库数据恢复-Oracle数据库数据恢复案例
数据库数据恢复环境: Oracle数据库ASM磁盘组有4块成员盘。 数据库故障&分析: Oracle数据库ASM磁盘组掉线 ,ASM实例无法挂载,用户联系我们要求恢复oracle数据库。 数据库数据恢复工程师拿到磁盘后,先将所有磁盘以只…...

对于msvcr120.dll丢失的问题,分享几种解决方法
msvcr120.dll的作用是提供一系列的运行时函数和功能,以便应用程序能够正常运行。这些函数和功能包括内存管理、异常处理、输入输出操作、数学运算等。在没有这个库文件的情况下,应用程序可能无法正常启动或执行特定的功能,甚至会出现错误提示…...
网络安全进阶学习第十三课——SQL注入Bypass姿势
文章目录 一、等号被过滤二、substr、mid等被过滤三、逗号被过滤四、and/or被过滤五、空格被过滤五、其他绕过方式 一、等号被过滤 1、like,rlike语句,其中rlike是正则2、大于号>,小于号<3、符号<>:<>为不等于…...

vue3 provide inject实现强制刷新
1、在 App.vue 文件里写入 provide 的方法 <template> <div id"app"><keep-alive> <router-view v-if"isRouterAlive"></router-view></keep-alive> </div> </template> <script> export default …...
Neo4j笔记-数据迁移(导出/导入)
这里先说明以下几点: Neo4j在4.0下版本默认的库名是:graph.db Neo4j在4.0上版本默认的库名是:neo4j.db 不管是Neo4j,还是Neo4j Desktop,都会在bin目录下有neo4j、neo4j-admin软件。在conf目录下,有neo4j.…...
请求转发和请求重定向
目录 1. 定义层面 2. 请求方层面 3. 数据共享层面 4. 最终 url 层面 5. 代码实现层面 请求转发 请求重定向 在Java中,跳转网页的方式有两种,一种是请求转发,另一种是请求重定向,而实际上,这两种方式是有着明显…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
