Dijkstra(求最短路)
时间复杂是 O(n2+m) ,n 表示点数,m 表示边数
模板(朴素法一般m等于n^2的时候使用)
#include<bits/stdc++.h>
#include<algorithm>
using namespace std;
const int N=510;
int g[N][N]; //为稠密阵所以用邻接矩阵存储
int dist[N]; //用于记录每一个点距离第一个点的距离
bool st[N]; //用于记录该点的最短距离是否已经确定int Dijkstra()
{memset(dist, 0x3f,sizeof dist); //初始化距离 0x3f代表无限大dist[1]=0; //第一个点到自身的距离为0for(int i=0;i<n;i++) //有n个点所以要进行n次 迭代{int t=-1; //t存储当前访问的点for(int j=1;j<=n;j++) //这里的j代表的是从1号点开始if(!st[j]&&(t==-1||dist[t]>dist[j])) t=j;st[t]=true; //找到了距离最小的点t,并用最小的点t去更新其他的点到起点的距离for(int j=1;j<=n;j++)dist[j]=min(dist[j],dist[t]+g[t][j]);}if(dist[n]==0x3f3f3f3f) return -1; //如果第n个点路径为无穷大即不存在最低路径return dist[n];
}
int main()
{cin>>n>>m;memset(g,0x3f,sizeof g); //初始化图 因为是求最短路径//所以每个点初始为无限大while(m--){int x,y,z;cin>>x>>y>>z;g[x][y]=min(g[x][y],z); //如果发生重边的情况则保留最短的一条边}cout<<Dijkstra()<<endl;return 0;
}模板(堆优化版一般在m等于n的时候使用)
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair<int,int>PII; //堆里储存距离和编号
const int N=1e6+10;
int n,m;
int h[N],w[N],e[N],ne[N],idx; //对于每个点k,开一个单链表,存储K所有可以走到的点,h[k]存储这个单链表的头节点
int dist[N]; //存储距离
bool st[N]; //储存状态//添加一条a到b的边
void add(int a,int b,int c){e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++; }int Dijkstra()
{memset(dist,0x3f,sizeof dist); //距离初始化为最大值dist[1]=0;priority_queue<PII,vector<PII>,greater<PII>>heap; //小根堆heap.push({0,1}); //插入距离和节点编号while(heap.size()){auto t=heap.top(); //取距离原点最近的点heap.pop();int ver=t.second,distance=t.first; if(st[ver])continue; //如果该点已经确定,则跳过该点st[ver]=true;for(int i=h[ver];i!=-1;i=ne[i])//更新ver所指向的节点距离{int j=e[i];if(dist[j]>dist[ver]+w[i]){dist[j]=dist[ver]+w[i];heap.push({dist[j],j}); //最小距离入堆 } } } if(dist[n]==0x3f3f3f3f)return -1;return dist[n];
}int main(){cin>>n>>m;memset(h,-1,sizeof h);while(m--){int x,y,z;cin>>x>>y>>z;add(x,y,z);}cout<<Dijkstra()<<endl;return 0;
} 相关文章:
)
Dijkstra(求最短路)
时间复杂是 O(n2m) ,n 表示点数,m 表示边数 模板(朴素法一般m等于n^2的时候使用) #include<bits/stdc.h> #include<algorithm> using namespace std; const int N510; int g[N][N]; //为稠密阵所以用邻接矩阵存储 int dist[N]; //用…...

React 脚手架
1.React 定义 React 脚手架(React boilerplate)是一种预先设置好的、可以快速启动 React 项目的工具。脚手架已经包含了 React、Webpack、Babel、ESLint、Jest 等一些常用的工具和库,并已经配置好了这些工具的参数,可以直接使用和…...

CTFSHOW php命令执行
目录 web29 过滤flag web30 过滤system php web31 过滤 cat|sort|shell|\. 这里有一个新姿势 可以学习一下 web32 过滤 ; . web33 web34 web35 web36 web37 data伪协议 web38 短开表达式 web39 web40 __FILE__命令的扩展 web41 web42 重定向…...

侧滑置顶,取消置顶
第一步:布局 <?xml version"1.0" encoding"utf-8"?> <com.ddmh.magic.camera.ui.widget.SwipeMenuLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"http://schemas.android.com/apk/res-auto"…...
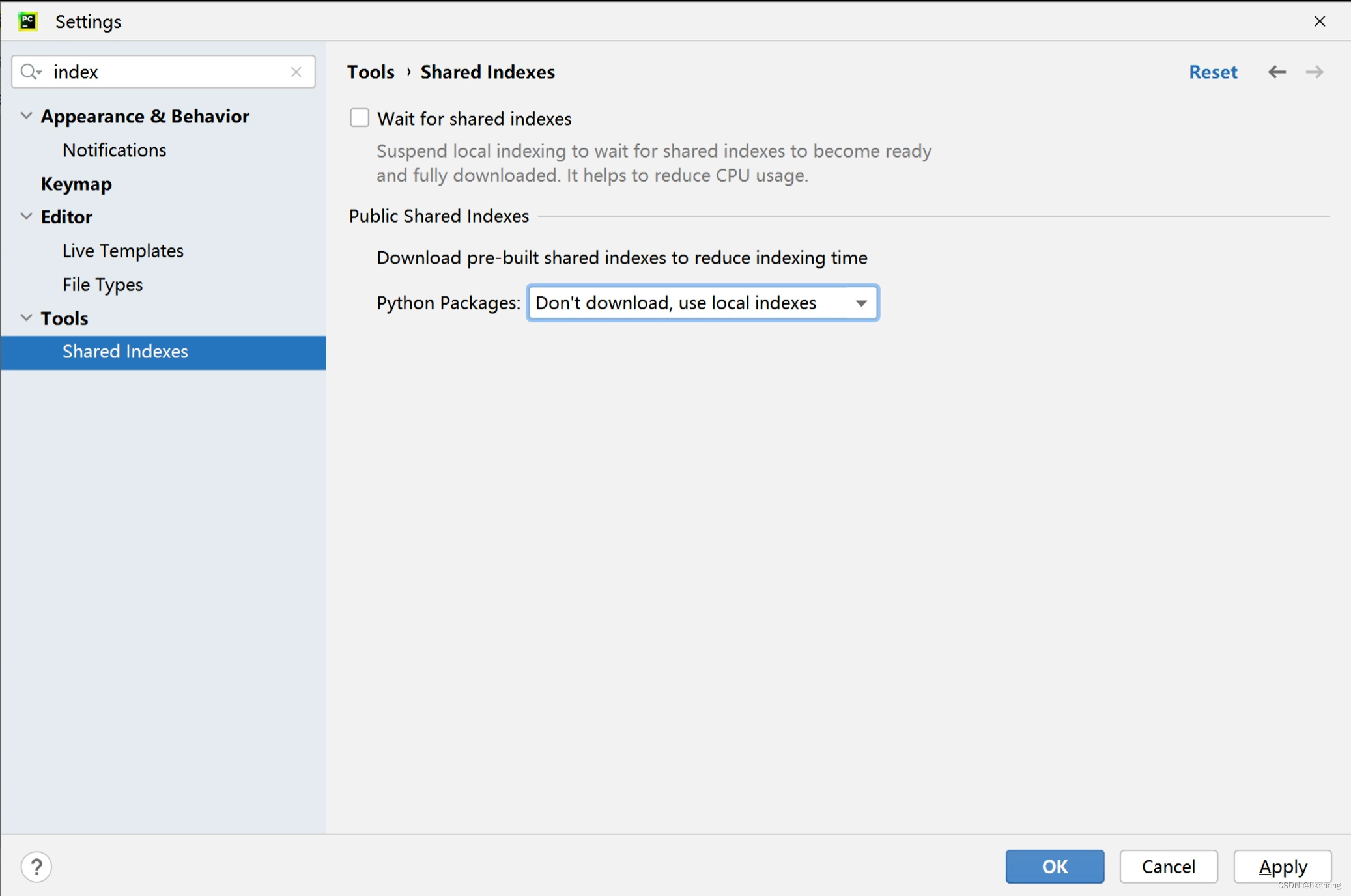
Pycharm解决启动时候索引慢的问题
设置里去掉update里面的两个勾 shared indexes中,把自动下载索引改成不下载使用本地索引...

Http请求响应时间一般划分标准
HTTP请求的响应时间被认为是长或短通常取决于具体应用场景和性能需求。一般来说,以下是一些常见的对HTTP请求响应时间进行划分的标准: 即时响应:通常在毫秒级别的响应时间被认为是即时响应。这适用于对实时性要求较高的应用,如实时…...
生成测试报告,在Unittest框架中就是简单
测试套件(Test Suite)是测试用例、测试套件或两者的集合,用于组装一组要运行的测试(多个测试用例集合在一起)。 (1)创建一个测试套件: import unittest suite unittest.TestSuite…...
)
生成式人工智能的潜在有害影响与未来之路(一)
这是本文的第1版,反映了截至2023年5月15日,Generative AI的已记载的和预期的危害。由于Generative AI的发展、使用和危害的快速变化,我们承认这是一篇内在的动态论文,未来会发生变化。 在本文中,我们使用一种标准格式…...

lightdb23.3 表名与包名不能重复
LightDB 表名与包名不能重复 从 LightDB 23.3 版本开始表名和包名不能重复,与 oracle 一致。原先已已支持包名和schema名不能重复。 背景 在之前版本在同一schema 下可以创建相同名字的表和包。这会导致在存储过程中使用%type指定变量类型时,如果存在…...

Oracle 开发篇+Java通过HiKariCP访问Oracle数据库
标签:HikariCP、数据库连接池、JDBC连接池、释义:HikariCP 是一个高性能的 JDBC 连接池组件,号称性能最好的后起之秀,是一个基于BoneCP做了不少的改进和优化的高性能JDBC连接池。 ★ Java代码 import java.sql.Connection; impor…...
进销存管理系统(小杨国贸)springboot采购仓库财务java jsp源代码mysql
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 进销存管理系统(小杨国贸)spri…...
)
指针初阶(2)
文章目录 5. 指针和数组6. 二级指针7. 指针数组 附: 5. 指针和数组 指针变量:指针变量就是指针变量,不是数组,指针变量的大小是4/8个字节,专门是用来存放地址的。 数组:数组就是数组,不是指针&a…...
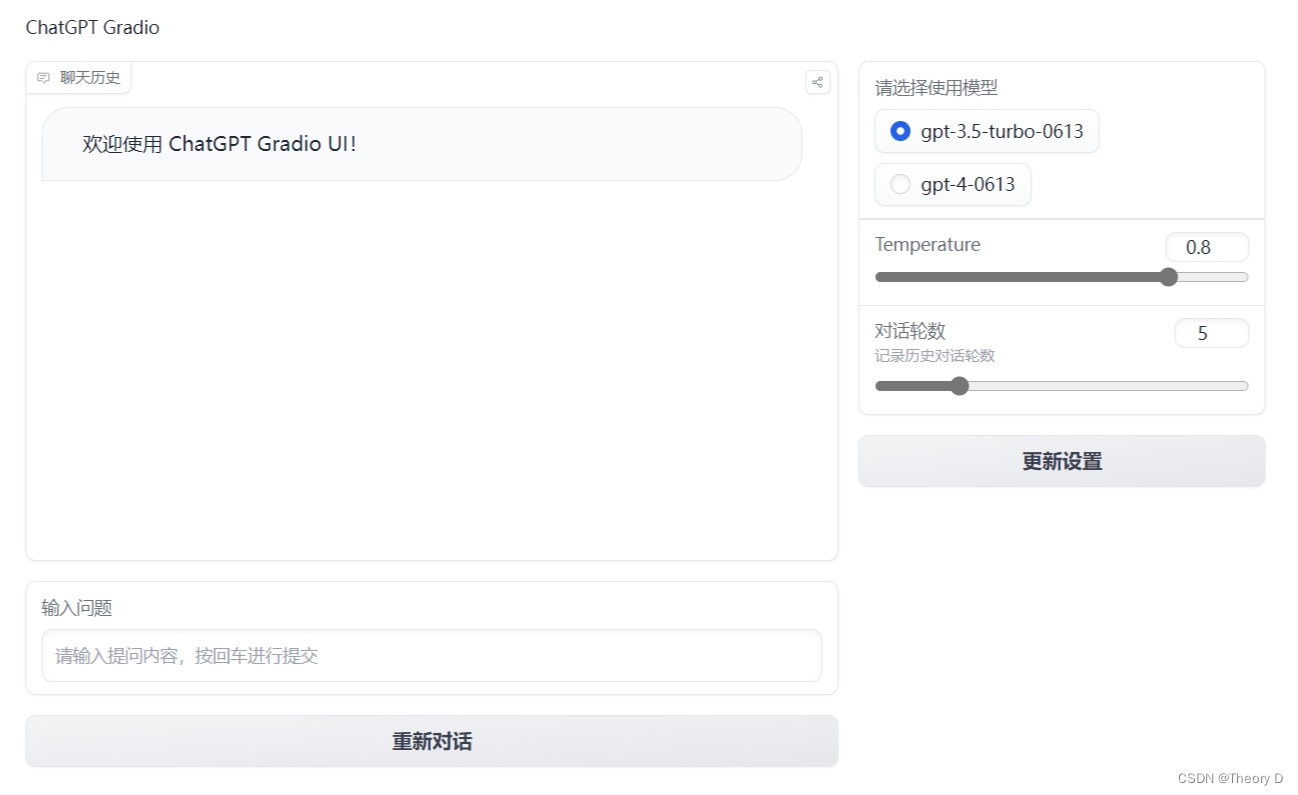
基于Gradio的GPT聊天程序
网上很多别人写的,要用账号也不放心。就自己写了一个基于gradio的聊天界面,部署后可以本地运行。 特点: 可以用openai的,也可以用api2d,其他api可以自己测试一下。使用了langchain的库 可以更改模型,会的…...

包管理工具详解npm 、 yarn 、 cnpm 、 npx 、 pnpm(2023)
1、包管理工具npm (1)包管理工具npm: Node Package Manager,也就是Node包管理器;但是目前已经不仅仅是Node包管理器了,在前端项目中我们也在使用它来管理依赖的包;比如vue、vue-router、vuex、…...

Terraform 系列-批量创建资源时如何根据某个字段判断是否创建
系列文章 Terraform 系列文章Grafana 系列文章 概述 前文 Grafana 系列 - Grafana Terraform Provider 基础 介绍了使用 Grafana Terraform Provider 创建 Datasource. 这几天碰到这么一个现实需求: 使用 Terraform 批量创建日志数据源时, 有的数据源类型是 El…...

Android侧滑栏(一)可缩放可一起移动的侧滑栏
在实际的各类App开发中,经常会需要做一个左侧的侧滑栏,类似于QQ这种。 今天这篇文章总结下自己在开发中遇到的这类可以跟随移动且可以缩放的侧滑栏。 一、实现原理 使用 HorizontalScrollView 实现一个水平方向的可滑动的View,左布局为侧滑…...
简单程度与自负是否相关?探索STM32的学习价值
事实上,无论STM32是否简单并不重要,更重要的是我们能通过学习STM32获得什么。通过STM32,我们可以学习到许多知识:如果我们制作一个键盘或鼠标,我们可以学习USB协议。如果我们制作一个联网设备,我们需要学习…...
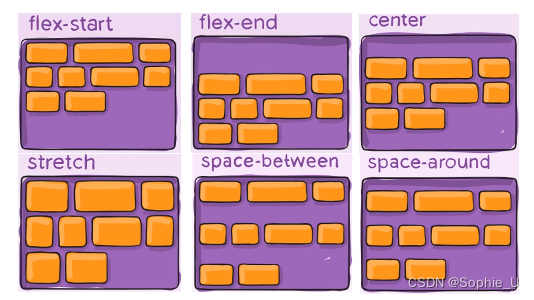
第二章:CSS基础进阶-part3:弹性例子布局
文章目录 Flex盒模型二、常见属性2.1 flex属性2.2 justify-content2.3 flex-wrap2.4 flex-flow2.5 align-items2.6 父容器-align-content Flex盒模型 1、普通盒模型 2、弹性盒布局 使用弹性盒布局能让容器的宽度跟随浏览器窗口的变化而变换 二、常见属性 2.1 flex属性 2.2 …...

函数与方法有区别?
有区别,当然是有区别。 不管是java、rust还是go,他们都是不一样的。 先看定义: 函数(Function) 是一段独立的代码块,用于执行特定的任务。函数可以被多次调用,并且可以接受参数和返回结果。在G…...
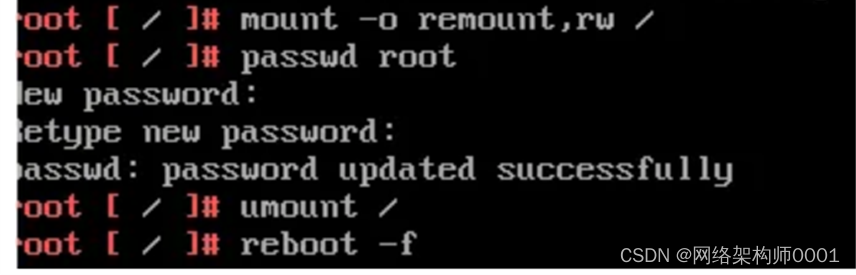
VMware vCenter忘记密码操作,和Linus原理一致
mount -o remount,rw / passwd root ## 修改 root 密码要选择对应账户## 输入新密码,再输入一次新密码 umount / ## 卸载根文件系统 reboot -f ## 重新引导 vCenter...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
