C#与halcon联合 缩放移动自适应图像
读取图片
//获取文件路径下的图片public HObject GetImgFromPath(string imgPath){HObject L_Img;HOperatorSet.GenEmptyObj(out L_Img);//清空图片L_Img.Dispose();//释放HOperatorSet.ReadImage(out L_Img, imgPath);//读取图片存入到l_imgreturn L_Img;}
拉伸显示
//图片拉伸显示public void ImgIsStretchDisplay(HObject L_Img, HTuple Hwindow){HTuple hv_Width,hv_Height;HOperatorSet.ClearWindow(Hwindow);//清空画面HOperatorSet.GetImageSize(L_Img, out hv_Width, out hv_Height);//获取图片大小规格HOperatorSet.SetPart(Hwindow, 0, 0, hv_Height, hv_Width);//设置窗体的规格HOperatorSet.DispObj(L_Img, Hwindow);//显示图片}
不拉伸,原图比例显示
//图片不拉伸显示public void ImgIsNotStretchDisplay(HObject L_Img, HTuple Hwindow){HTuple hv_Width, hv_Height;HTuple win_Width, win_Height, win_Col, win_Row, cwin_Width, cwin_Height;HOperatorSet.ClearWindow(Hwindow);HOperatorSet.GetImageSize(L_Img, out hv_Width, out hv_Height);//获取图片大小规格HOperatorSet.GetWindowExtents(Hwindow, out win_Row, out win_Col, out win_Width, out win_Height);//获取窗体大小规格cwin_Height = 1.0 * win_Height / win_Width * hv_Width;//宽不变计算高 if (cwin_Height > hv_Height)//宽不变高能容纳{cwin_Height = 1.0 * (cwin_Height - hv_Height) / 2;HOperatorSet.SetPart(Hwindow, -cwin_Height, 0, cwin_Height + hv_Height, hv_Width);//设置窗体的规格}else//高不变宽能容纳{cwin_Width = 1.0 * win_Width / win_Height * hv_Height;//高不变计算宽cwin_Width = 1.0 * (cwin_Width - hv_Width) / 2;HOperatorSet.SetPart(Hwindow, 0, -cwin_Width, hv_Height, cwin_Width + hv_Width);//设置窗体的规格}HOperatorSet.DispObj(L_Img, Hwindow);//显示图片}
图像缩放
解决缩太小崩溃问题,联合鼠标滚轮事件
//图片缩小放大,配合鼠标滚轮事件public void ImgZoom(HObject L_Img, HTuple Hwindow, int Delta = 0){HTuple Zoom, Row, Col, L_Button;HTuple hv_Width, hv_Height;HTuple Row0, Column0, Row00, Column00, Ht, Wt;HTuple[] Now_Pos = new HTuple[4];if (Delta > 0)//鼠标滚动格值,一般120{Zoom = 1.2;//向上滚动,放大倍数}else{Zoom = 0.8;//向下滚动,缩小倍数}HOperatorSet.GetMposition(Hwindow, out Row, out Col, out L_Button);//获取当前鼠标的位置HOperatorSet.GetPart(Hwindow, out Row0, out Column0, out Row00, out Column00);//获取当前窗体的大小规格HOperatorSet.GetImageSize(L_Img, out hv_Width, out hv_Height);//获取图片大小规格Ht = Row00 - Row0;Wt = Column00 - Column0;if (Ht * Wt < 32000 * 32000 || Zoom == 1.2){Now_Pos[0] = (Row0 + ((1 - (1.0 / Zoom)) * (Row - Row0)));Now_Pos[1] = (Column0 + ((1 - (1.0 / Zoom)) * (Col - Column0)));Now_Pos[2] = Now_Pos[0] + (Ht / Zoom);Now_Pos[3] = Now_Pos[1] + (Wt / Zoom);HOperatorSet.SetPart(Hwindow, Now_Pos[0], Now_Pos[1], Now_Pos[2], Now_Pos[3]);HOperatorSet.ClearWindow(Hwindow);HOperatorSet.DispObj(L_Img, Hwindow);}else{ImgIsNotStretchDisplay(L_Img, Hwindow);//不拉伸显示}}
图像移动,实时移动
解决移动太快图像刷新闪烁问题
HTuple oldRow, oldColumn;//鼠标按下去拖着图像移动,配合鼠标坐标按下与移动事件public void MouseDownMoveImg(HObject L_Img, HTuple Hwindow){HTuple row1, col1, row2, col2, Row, Column, Button;HOperatorSet.GetMposition(Hwindow, out Row, out Column, out Button);double RowMove = Row - oldRow; double ColMove = Column - oldColumn;HOperatorSet.GetPart(Hwindow, out row1, out col1, out row2, out col2);//得到当前的窗口坐标HOperatorSet.SetPart(Hwindow, row1 - RowMove, col1 - ColMove, row2 - RowMove, col2 - ColMove);//防止刷新图片太快的时候闪烁HOperatorSet.SetSystem("flush_graphic", "false");HOperatorSet.ClearWindow(Hwindow);HOperatorSet.SetSystem("flush_graphic", "true");//HOperatorSet.DispObj(L_Img, Hwindow);}public void SaveMouseDownPosition(HTuple Hwindow){HTuple Button;HOperatorSet.GetMposition(Hwindow, out oldRow, out oldColumn, out Button);}
图像自适应
这里我们采用不拉伸显示函数
//设置自动适应private void tsMAutoFit_Click(object sender, EventArgs e){try{ImgIsNotStretchDisplay(ho_Image1, hWindowControl1.HalconWindow);}catch (Exception){MessageBox.Show("自适应失败,请插入图像!");} }相关文章:

C#与halcon联合 缩放移动自适应图像
读取图片 //获取文件路径下的图片public HObject GetImgFromPath(string imgPath){HObject L_Img;HOperatorSet.GenEmptyObj(out L_Img);//清空图片L_Img.Dispose();//释放HOperatorSet.ReadImage(out L_Img, imgPath);//读取图片存入到l_imgreturn L_Img;}拉伸显示 //图片拉…...

推荐 4 个 yyds 的 GitHub 项目
本期推荐开源项目目录: 1. 开源的 Markdown 编辑器 2. MetaGPT 3. SuperAGI 4. 一个舒适的笔记平台 01 开源的 Markdown 编辑器 Cherry 是腾讯开源的 Markdown 编辑器,基于 Javascript具有轻量简洁、易于扩展等特点, 它可以运行在浏览器或服…...

chrome插件开发实例05-页面间通信
目录 一、页面间通信的方式 方式1: 通过消息通信...
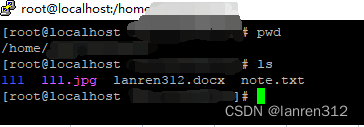
linux安装ftp
一、安装 参考博客 https://blog.csdn.net/dafeigecsdn/article/details/126518069 rpm -qa |grep vsftpd # 查看是否安装ftp yum -y install vsftpd # 安装vsftpuseradd -d /home/lanren312 lanren312 # 指定在/home目录下创建用户 passwd lanren312 # 给用户设置密码 # 输…...
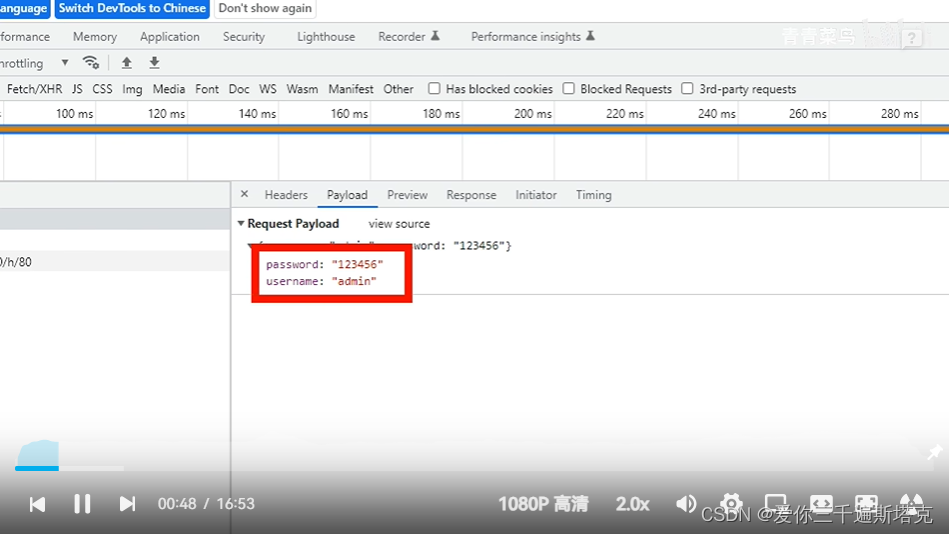
前后端分离------后端创建笔记(上)
本文章转载于【SpringBootVue】全网最简单但实用的前后端分离项目实战笔记 - 前端_大菜007的博客-CSDN博客 仅用于学习和讨论,如有侵权请联系 源码:https://gitee.com/green_vegetables/x-admin-project.git 素材:https://pan.baidu.com/s/…...

Java不可变集合详解
什么是不可变集合 不可变集合,英文叫 immutable 顾名思义就是说集合是不可被修改的。集合的数据项是在创建的时候提供,并且在整个生命周期中都不可改变。 为什么要使用不可变集合 不可变对象有很多优点,包括: 当对象被不可信的…...

常见的JavaScript日常问题
在众多的编程语言中, JavaScript 给大部分的人的第一印象是人畜无害,看起来就简单的,对稍微有点儿开发经验的人来说,在网页中写个JavaScript功能也相当简单。但是当你真的得了解了JavaScript之后就会发现,它比我们想象…...

css modules的用法和在react项目中的应用
参考文章 CSS Modules 的用法 CSS Modules 的功能很单纯,只加入了局部作用域和模块依赖,可以保证某个组件的样式,不会影响到其他组件。 局部作用域 CSS的规则都是全局的,任何一个组件的样式规则,都对整个页面有效。…...
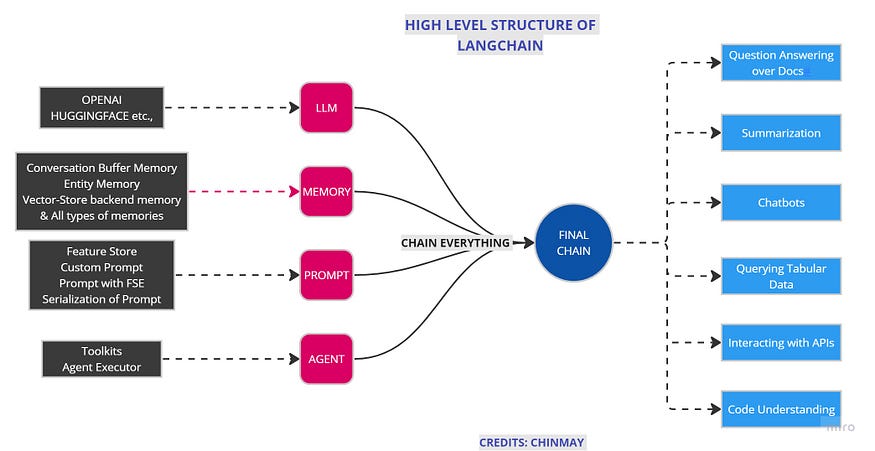
【LangChain概念】了解语言链️:第2部分
一、说明 在LangChain的帮助下创建LLM应用程序可以帮助我们轻松地链接所有内容。LangChain 是一个创新的框架,它正在彻底改变我们开发由语言模型驱动的应用程序的方式。通过结合先进的原则,LangChain正在重新定义通过传统API可以实现的极限。 在上一篇博…...

步入React前厅 - Css In React
目录 扩展学习资料 行内样式 引入样式表 CSS Module /src/components/common.module.css /src/components/listitem.module.css css管理进阶 Css管理工具 练习 扩展学习资料 资料名称 链接 css module CSS Modules 用法教程 - 阮一峰的网络日志 在React中使…...
——图像分割(二))
OpenCV(三)——图像分割(二)
目录 4.边缘检测 4.1 图像梯度的概念 4.2 模板卷积和梯度图的概念 4.3 梯度算子...
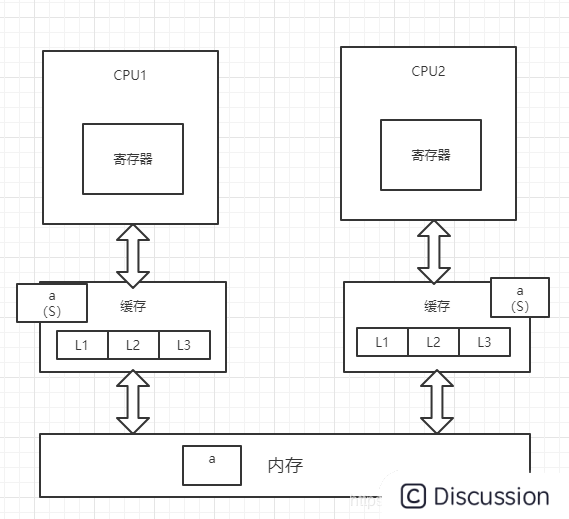
28.Netty源码之缓存一致性协议
Mpsc Queue 基础知识 Mpsc 的全称是 Multi Producer Single Consumer,多生产者单消费者。Mpsc Queue 可以保证多个生产者同时访问队列是线程安全的,而且同一时刻只允许一个消费者从队列中读取数据。 Netty Reactor 线程中任务队列 taskQueue 必须满足多个…...

造个轮子-任务调度执行小框架-任务清单执行恢复实现
文章目录 前言恢复执行流程失败任务执行重启执行中任务恢复执行修复组件整合组件整合容器启动类总结前言 okey,通过前面的两篇文章,关于这个任务执行这一块,我想应该是明白了。但是这里的话,还是不够的。我们希望对于任务还可以做到执行失败的重试执行,关于这个意外宕机的…...

若依部署前后端
打包项目 前端打包 npm run build:prod将代码上传到指定目录 配置nginx转发 server{listen 8090;server_name localhost;location / {root /home/cc_library/dist;index index.html index.htm;# 配置 history模式,刷新页面会404,,因为服…...

2009年上半年 软件设计师 下午试卷
博主介绍:✌全网粉丝3W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验…...

SpringBoot使用自定义事件监听器的demo
记录一下SpringBoot自定义事件监听器的使用方法 案例源码:SpringBoot使用自定义事件监听器的demo 使用的SpringBoot2.0.x版本 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><…...

arcgis定义投影与投影
1、定义 地理坐标系(GCS):利用地球表面的经纬度表示的坐标系统。一般单位为度。投影坐标系(PCS):利用数学换算将三维地球表面上的经纬度坐标转换到二维平面上的坐标系统。一般单位为米。可以认为ÿ…...
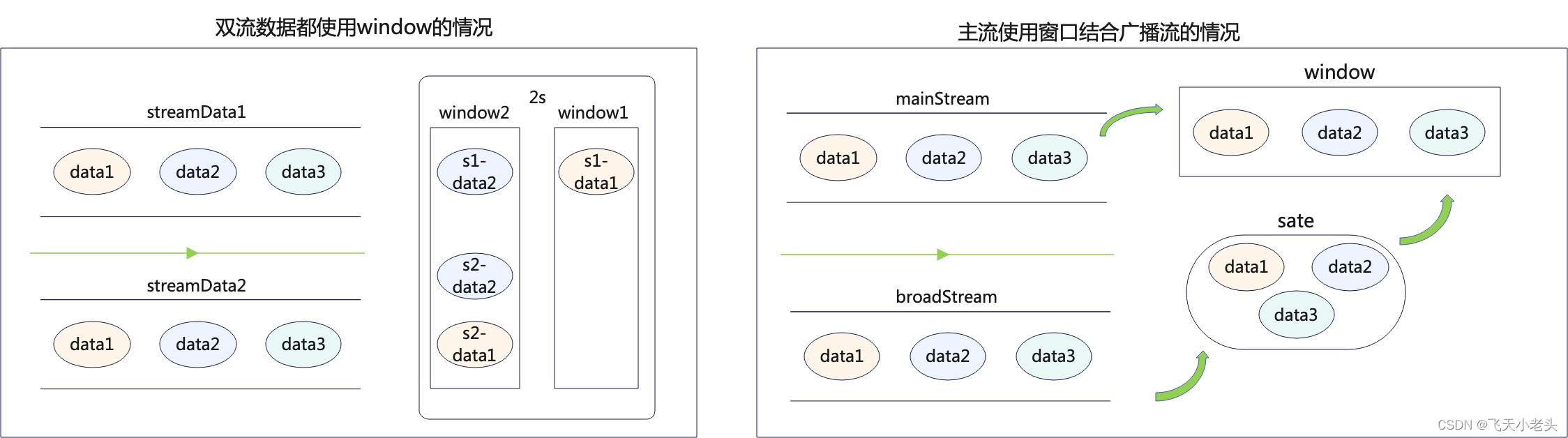
Flink多流处理之Broadcast(广播变量)
写过Spark批处理的应该都知道,有一个广播变量broadcast这样的一个算子,可以优化我们计算的过程,有效的提高效率;同样在Flink中也有broadcast,简单来说和Spark中的类似,但是有所区别,首先Spark中的broadcast是静态的数据,而Flink中的broadcast是动态的,也就是源源不断的数据流.在…...
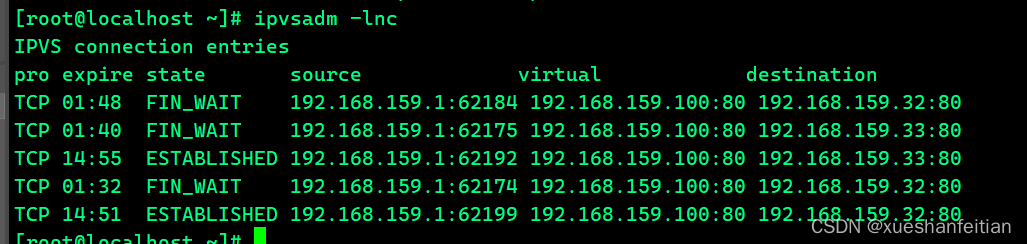
LVS/DR+Keepalived负载均衡实战(一)
引言 负载均衡这个概念对于一个IT老鸟来说再也熟悉不过了,当听到此概念的第一反应是想到举世闻名的nginx,但殊不知还有一个大名鼎鼎的负载均衡方案可能被忽略了,因为对于一般系统来说,很多应用场合中采用nginx基本已经满足需求&a…...

测试DWPose的onnx +Unity barracuda
环境: Unity Barracuda 3.0.1 从github直接拉取的barracuda仓库才能装到这个版本Barracuda以后不再升级了,会迁移到Unity AI大计划里的Sentis 我想申请的来着但好像已经不开放了 Unity 2021.3.20模型:dw-ll_ucoco_384.onnx 报了一些错&…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
